基于粒子群优化算法的功放预失真处理

董　元, 王勇超

(1. 西安邮电大学 研究生院， 陕西 西安 710121;　2.西安电子科技大学 通信工程学院， 陕西 西安 710071)

基于粒子群优化算法的功放预失真处理

董元1, 王勇超2

(1. 西安邮电大学 研究生院， 陕西 西安 710121;2.西安电子科技大学 通信工程学院， 陕西 西安 710071)

摘要:根据功率放大器的记忆非线性特性，给出一种基于粒子群优化算法的预失真处理方法。选取记忆非线性多项式作为预失真器模型，用粒子群优化算法对多项式的系数进行最优估计，获得预失真器模型参数。分别对连块Wiener模型和记忆多项式模型这两种经典功率放大器模型进行预失真处理，结果表明，所给方法对记忆非线性功放的线性化效果良好，可正确判别发送信号。

关键词:功率放大器；粒子群优化算法；记忆效应；预失真

功率放大器(功放)是通信发射机中必不可少的部件。一方面，为提高效率，被安排在接近饱和点处的功放具有明显非线性，会使信号产生严重带内失真和带外频谱再生，前者会降低系统的误码性能，后者会引起邻道干扰。另一方面，用于放大宽带信号的功放会产生记忆效应，当前输出不再只由当前输入决定，还与过去的输入和输出有关。记忆效应和非线性纠缠在一起，增大了功放线性化的难度。常用的线性化处理技术是在非线性放大器前端放置一个可调的、特性曲线与功放特性曲线互补的非线性模型，即预失真处理。

目前成熟的基带预失真技术有将Volterra级数用于预失真器的设计[1-2]，但实现复杂度高且运算量大。基于二维查询表的改进预失真模型[3]、基于Wiener功放模型的Hamerstein预失真器[4]和一种包含隐层节点的神经网络预失真器[5]，只适用于记忆效应较弱的功放系统。

粒子群优化算法(ParticleSwarmOptimization,PSO)[6]来源于人工生命和演化计算理论，是基于群体的演化算法。PSO算法在求解连续函数的优化问题时，具有很强通用性，应用领域较为广泛，在训练人工神经网络、多目标优化问题，动态系统跟踪、数据挖掘，参数估计[6]方面都有应用。

本文选取记忆非线性多项式为预失真器模型，用PSO算法对预失真器的系数进行最优估计，并仿真分析整个系统线性化性能。

1基于PSO算法的预失真处理

以一个记忆多项式作为预失真模块，如图1所示，采用非直接学习结构，对通过功放模块,并经归一化处理的信号，应用基于最小均方误差准则的自适应迭代算法，以PSO算法对预失真模块A的系数进行估计，得到功放的一个近似逆，然后将预失真模块A的参数直接拷贝到预失真模块B中，获得整个系统模型。

图1　基于PSO算法的预失真系统

1.1记忆功放模型

记忆功放模型须综合考虑功放记忆效应和非线性，基于此类功放模型的输入输出信号由于记忆效应而不再具有一一对应关系。

Volterra级数模型在理论上可精确描述功放在任意状态下的特征，本文采用它的两种简化模型——Winner模型和记忆多项式模型作为记忆功放模型，分别进行线性化预失真处理。

1.1.1Wiener-Hammerstein模型

Wiener-Hammerstein(W-H)模型由一个线性时不变系统(lineartimeinvariant,LTI)，后继一个无记忆非线性模块，再接另一个线性时不变系统[7]组成，如图2所示。这种模型结构经常被用作描述卫星透明转发器在临近饱和区工作时的系统特性。

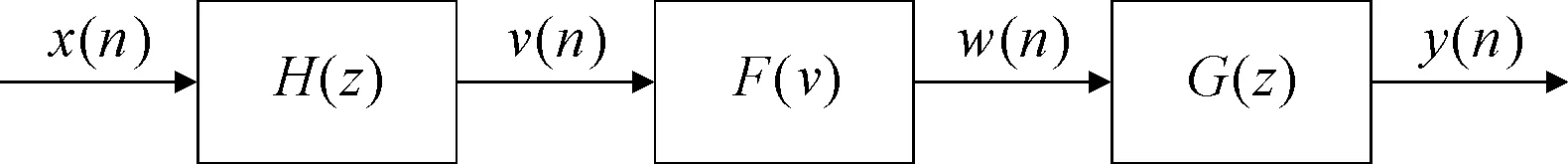
图2W-H连块模型

模型中两个LTI分别定义为

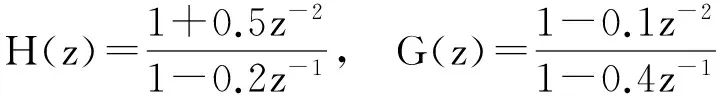
无记忆非线性模块为

其中

b1=1.010 8+0.085 8 j,

b3=0.087 9-0.158 3 j,

b5=-1.099 2-0.889 1 j。

1.1.2记忆多项式模型

记忆多项式模型为

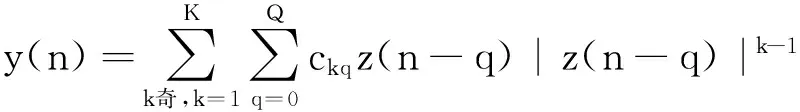
其中:K为最高非线性阶数；Q为延迟因子，是模型记忆的直接反映，当Q=0时，此多项式为无记忆非线性系统；ckq为复数系数，其取值直接影响模型的非线性。

1.2预失真模型参数估计

令预失真模块A服从一个奇数阶记忆多项式模型

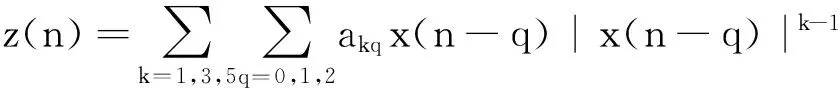
求解最优复系数akq步骤描述如下。

步骤1初始化PSO：初始化每个粒子的位置和速度，求出初始的Pbest和Gbest值，以Gbest值作为akq的值。

步骤2将16-QAM信号经过升余弦脉冲成型后，采样得到的序列通过如图1所示的系统。

步骤3以最小均方误差函数作为PSO算法的适应度函数，计算适应度值。

步骤4判断其是否满足结束条件：适应度值是否符合要求——均方误差达到要求精度，或迭代代数达到最大迭代数Tmax。若条件不满足，更新粒子群，转到步骤c，进行新一轮迭代；若满足条件，则停止迭代。

采用PSO算法迭代，最后获得一组全局最优解Gbest，即为所求预失真器A的系数，将其直接拷贝到预失真模块B中，完成整个参数估计，构成线性化系统模型。

1.3误差矢量值估计数字调制信号

误差矢量值(errorvectormagnitude,EVM)为理论理想点和接收信号间的误差[7-8],如图3所示，可用来衡量通过非线性功放后接收信号的偏移程度。

图3　误差矢量

EVM的均方估计为

2仿真结果

采用Matlab语言对本文算法进行仿真实验。

2.1功放采用W-H模型

将16-QAM信号直接通过W-H模型，所得星座图如图4所示，可见，输出信号的幅度和相位都发生了非常严重的畸变，无法判决，其中

e2=326.18。

图4　直接经W-H模型输出信号星座图

对图1所示系统基带模型，用PSO算法来估算预失真器模型的参数，以最小均方误差函数为适应度函数进行迭代，获得预失真器的参数估计值，16-QAM信号通过预失真器，再通过W-H功放模型，所得信号星座图如图5所示。与信号直接通过W-H功放模型相比，信号的幅度和相位失真都有所改善，达到了线性化效果，可以正确判别信号，其中

e2=0.26。

图5　经预失真模块和W-H模型输出信号星座图

2.2功放采用记忆多项式模型

对记忆多项式功放模型，令

K=5，Q=2，

c10=1.051 3+0.090 4j,

c30=-0.024 2-0.290 0j,

c50=-0.965 7-0.702 8j,

c11=-0.068 0-0.102 3j,

c31=0.223 4+0.231 7j,

c51=-0.245 1-0.973 5j,

c12=0.708 9-0.605 4j,

c32=-1.062 1-0.393 2j,

c52=0.122 9+1.150 8j。

将16-QAM信号直接通过如上述的记忆多项式功放模型，所得星座图如图6所示，可见，信号在幅度和相位上都产生了不同程度的畸变，有

e2=64.56，

非线性失真比较严重。

图6　16-QAM信号直接通过记忆多项式功放模型

以最小均方误差函数为适应度函数，运用PSO算法估计预失真模块的参数， 16-QAM信号通过预失真模块和功放模块后，所得输出信号的星座图如图7所示，与信号直接通过W-H功放模型相比，信号的幅度和相位失真都有了明显的改善，基本达到了较好的线性化效果，完全可以正确判别信号，其

e2=0.15。

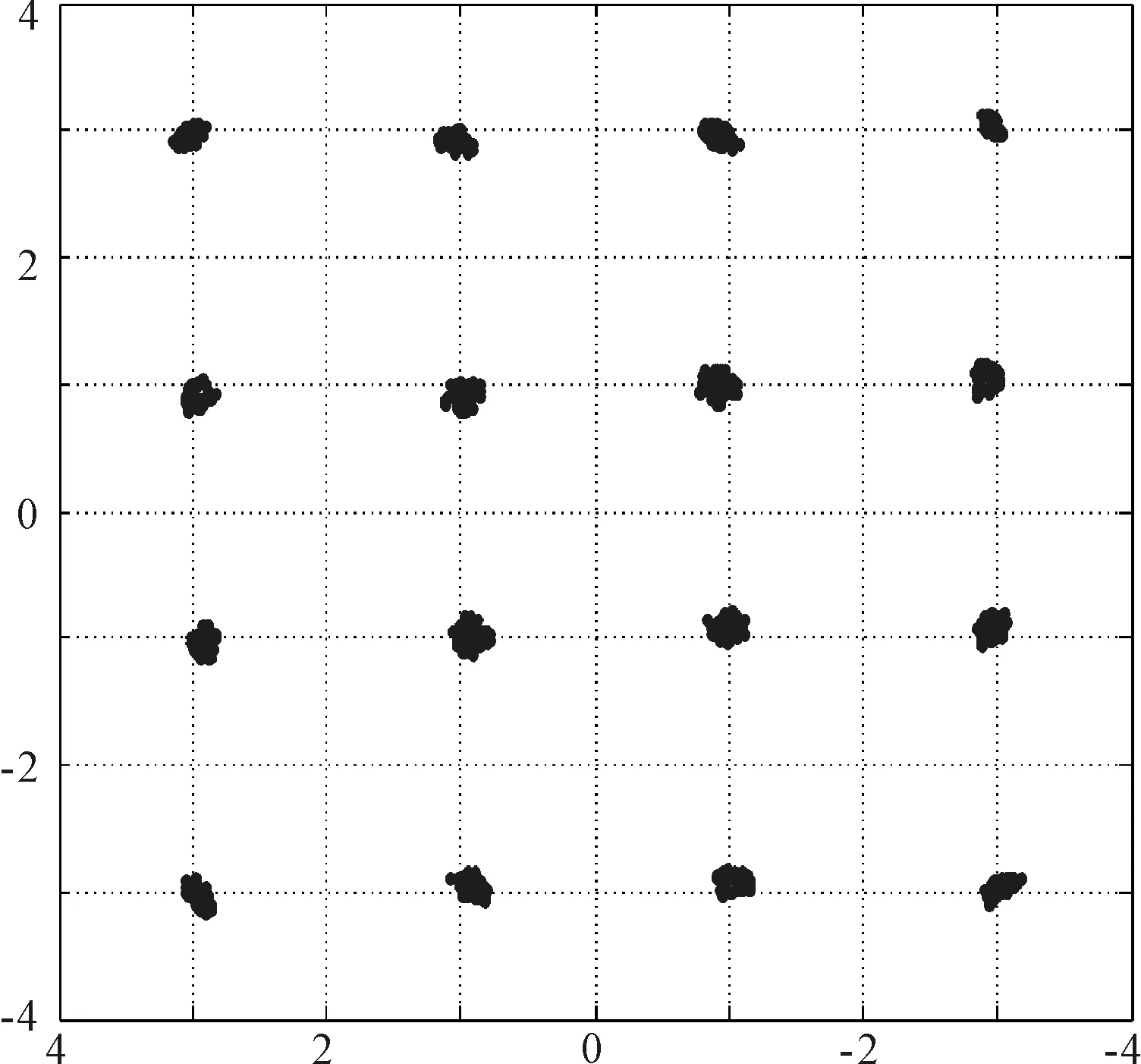
图7　16-QAM信号通过预失真模块再通过功放

3结语

将PSO算法用于记忆功率放大器预失真设计，仿真结果表明，这种基于PSO算法求解最优值的功率放大器预失真算法，对功放的记忆非线性有着较好的线性化效果。

参考文献

[1]EUNC,POWERSEJ.ANewVolterraPredistorterBasedontheIndirectLearningArchitecture[J].IEEETransactionsonSignalProcessing, 1997, 45(1):223-227.DOI:10.1109/78.552219.

[2]KIMJ,KONSTANTINOUK.DigitalPredistortionofWidebandSignalsbasedonPowerAmplifierModelwithMemory[J].ElectronicLetters, 2001, 37(23):1417-1418.DOI:10.1049/el:20010940.

[3]HEZY,GEJH,GENGSJ,etal.AnImprovedLook-UpTablePredistortionTechniqueforHPAwithMemoryEffectsinOFDMSystems[J].IEEETransactionsonBroadcasting,2006, 52(1):87-91.DOI:10.1109/TBC.2005.861608.

[4]陈凯亚，王敏锡.Wiener功放的分离预失真方法[J/OL].通信学报，2005, 26(9):31-34 [2015-05-12].http://www.cnki.com.cn/Article/CJFDTotal-TXXB200509004.htm.

[5]钱业清，姚天任.记忆非线性功放的神经网络预失真[J/OL].计算机工程与应用，2004,40 (21):100-103[2015-05-12].http://www.cnki.com.cn/Article/CJFDTotal-JSGG200421031.htm.

[6]董元,王勇,易克初. 粒子群优化算法发展综述[J/OL]. 商洛学院学报，2006，20(4): 28-32[2015-05-12].http://www.cnki.com.cn/Article/CJFDTotal-SLSF200604009.htm.

[7]董元,王勇,易克初. 一种记忆功率放大器自适应线性化仿真[J/OL].计算机技术与发展，2010，20(6) :217-220[2015-05-12].http://www.cnki.com.cn/Article/CJFDTotal-WJFZ201006056.htm.

[8]KUH.BehavioralModelingofNonlinearRFPowerAmplifiersforDigitalWirelessCommunicationSystemswithImplicationsforPredistortionLinearizationSystems[D/OL].Georgia:GeorgiaInstituteofTechnology, 2003:1-138[2015-05-12].http://hdl.handle.net/1853/5327.

[责任编辑:瑞金]

Apoweramplifierpredistortionprocessingmethodbasedonparticleswarmoptimization

DONGYuan1,WANGYongchao2

(1.SchoolofGraduate,Xi’anUniversityofPostsandTelecommunications,Xi’an710121,China;2.SchoolofTelecommunicationEngineering,XidianUniversity,Xi’an710071,China)

Abstract:According to the nonlinear characteristics of the power amplifier, a predistortion processing method based on particle swarm optimization algorithm is proposed. Select the memory nonlinear polynomial as a predistorter model, and use the particle swarm optimization algorithm to estimate the coefficients of the polynomials and to obtain the parameters of predistorter model. chose two kinds of classical power amplifier models, Wiener model and memory polynomial model, to execute the predistortion processing respectively, and the results show that, the proposed method linearize the memory nonlinear power amplifier well, it can find out the sending signal correctly.

Keywords:power amplifier, particle swarm optimization, memory effects, predistortion

doi:10.13682/j.issn.2095-6533.2016.02.017

收稿日期：2015-06-18

基金项目：西安邮电大学青年教师科研基金资助项目(ZL2013-23)

作者简介：董元(1982-)，女，讲师，从事通信信号处理研究。E-mail:dongyuan@xupt.edu.cn 王勇超(1975-)，男，副教授，从事通信信号处理研究。E-mail: ychwang@mail.xidian.edu.cn

中图分类号：TP391.9

文献标识码：A

文章编号：2095-6533(2016)02-0088-04