密码协议形式化分析中的逻辑规则精简

潘　进， 王小明， 谢青松

(1.西安通信学院 信息安全系, 陕西 西安 710106;　2.西安通信学院 12队, 陕西 西安 710106)

密码协议形式化分析中的逻辑规则精简

潘进1， 王小明2， 谢青松1

(1.西安通信学院 信息安全系, 陕西 西安 710106;2.西安通信学院 12队, 陕西 西安 710106)

摘要:针对密码协议形式化分析中初始规则集过大且不易收敛的问题，给出一种基于先验知识集进行逻辑规则精简的方法。在初始规则迭代过程中，使用等价逻辑树理论进行规则集的蕴含和合一化处理，缩小初始规则集，并使形成的新的逻辑规则集具有与初始规则集等价的推导能力。

关键词:形式化验证；初始规则集；规则蕴含；规则合一化

分析密码协议的安全性，有攻击检测和形式化分析两种方法。攻击检测直观且易于理解，但运用中带有很大的偶然性和不确定性。形式化分析方法具有理论完备、广泛适用、结论可靠的特点，是当前的研究热点。

经历基于知识和信念的模态逻辑理论[1]以及以通信序列进程为代表的模型检测理论[2]之后，对形式化分析方法的关注被更多地集中在包括π演算和串空间理论在内的定理证明方法上[3]。

以π演算为代表的进程演算，理论上是一种进程代数，是交互和并发系统的理论模型，能够以接近协议本身的语言来描述协议，精确刻画协议运行过程和运行环境，特别适合于密码协议的建模[4-5]，但进程演算的协议表述并不利于机器理解和推理，需要将其转换成便于机器理解和推理的协议逻辑规则表述。

对协议进程演算模型进行机器自动转换所得到的协议逻辑表述，往往是一个较为庞大并包括大量冗余信息的规则集，在其上直接进行安全属性推导，不仅计算效率低，甚至会导致不收敛问题。

利用不动点迭代发散的充分条件对不停机进行预测[6-7]，采用预先设定最大搜索深度、最大加密层次可以强制停机，或者通过空间剪枝规则限制状态搜索空间，也可缓解状态空间爆炸问题[8-9]，但初始集庞大而冗余的问题在理论上并没有得到解决。

本文基于攻击者的能力和知识，拟采用等价逻辑推导树方法对初始规则集进行蕴含与合一化精简，以使推理过程中的状态空间得到实质性压缩。

1逻辑规则的蕴含与合一化

Horn逻辑既能等价表述进程演算的语法、语义，又易于被计算机理解。依据各种理论建模的密码协议往往被转换成Horn逻辑表述，然后再对逻辑规则集合进行自动化推导。关于规则集合的精简问题只需针对Horn逻辑讨论即可。

设逻辑规则

R=H→C=F1∧F2∧…∧Fn，

其中H是规则的假设，C是规则的结论,Fi(i=1,2,…,n)表示H中的事实，一般是关于Horn逻辑中变量、名称或函数的谓语。

定义1对于两个带有变量的事实Fi和Fj，若存在一个变量替换σ使得

σFi=Fj，

则称Fi和Fj是可合一化的，并称σ为合一化因子。

定义2设有两条逻辑规则

R1=H1→C1,R2=H2→C2,

其中H1和H2为多重假设。如果存在合一化因子σ，使得

σC1=C2,σH1⊆H2,

则称R1蕴含R2，记为R1⟹R2。

定义3设有两条逻辑规则

R=H→C,R′=H′→C′,

如果存在F0∈H′，使得C和F0能够合一化，且σ为C和F0的最一般合一化因子，则存在新的合一化规则

R。F0R′=σ[H∪(H′{F0})]→σC′。

对合一化规则持续进行合一化，可不断推导出新规则，形成逻辑推导树。用η、η′和η″等表示逻辑推导树的节点，则合一化过程可表示如图1。

图1　合一化规则

根据逻辑推导树的相关理论，定义2中给出的蕴含概念和定义3中给出的合一化规则分别具有如下性质。

性质1如果逻辑规则R′⟹R，且一个逻辑推导树的节点η被标记为R，那么节点η也可被标记为R′。

证明假设H为逻辑树节点η的所有出边集合，C为它的一个入边，节点η被标记为R，则有

R⟹H→C。

又因为

R′⟹R，

所以

R′⟹H→C，

则节点η也可被标记为R′。

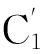
证明假设逻辑规则

R′=H′→C′，

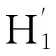
因此，存在合一化因子σ使得

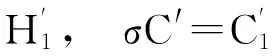
由于

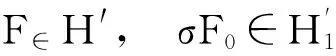
因此η′存在一个出边为σF0，假设这条边的终点为节点η，且η被标记为

R=H→C。

重新定义R中的变量，与R′中的变量进行区分。假设H1为节点η所有出边的集合，则可以得出

R⟹H1→σF0。

由此可扩展替换因子σ使得

σH⊆H1,σC′=σF0。

节点η′到节点η的边被标记为σF0，它为F0的一个实例。根据σC′=σF0，事实C和F0可以进行合一化，故可定义新规则R。F0R′。假设σ′为C和F0的最一般合一化因子，并定义σ=σ″σ′,则有

R。F0R′=σ′[H∪(H′{F0})]→σ′C′。

又因为

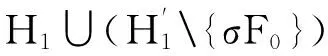
因此，可以得出

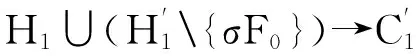
2逻辑规则精简算法

为了对安全属性有针对性地精简逻辑规则集，需要讨论相对于逻辑事实集合的选择函数。

定义4设有逻辑事实集合S，逻辑规则

R=H→C，

H中的事实F∈H。如果存在一个事实F′∈S和一个合一化因子σ，使得

σF=F′，

则称F合一化属于S，记为F∈rS。

定义5设有逻辑事实集合S，逻辑规则

R=H→C，

则称

为关于事实S的选择函数。

集合S通常是与攻击者的能力和知识有关的一个逻辑事实集合，fS(R)表示规则R假设中被选择出来进行S事实推导的假设。

设密码协议及其攻击者的进程演算模型已转换成初始规则集B0，其中包含描述攻击者攻击能力与知识的事实集合S。规则精简的目的就是要得到一个较小的逻辑集合B1，使得B1与B0具有等价的推导能力。所谓等价是指，在对所考虑的秘密性、认证性、匿名性等安全属性进行验证时，两个集合推导出的结论是完全相同的。精简结果与所考虑的安全属性有关，与攻击者的知识和能力有关。

逻辑规则精简算法的流程如图2所示,具体描述如下。

步骤1对于规则集B0中的每条规则R，判断是否对于R1∈B，有R1⟹R。若是，去除规则R；否则，将R加入规则集B中。

步骤2按步骤1处理完规则集B0中的每条规则后，依据选择函数是否为空将规则集B中的规则分成B′和B″两类，其中规则集B′中的每条逻辑规则都使选择函数为空，而规则集B″中的每条逻辑规则都使选择函数非空。

步骤3将规则集B′中的逻辑规则R′与规则集B″中的逻辑规则R″进行合一化处理，并将得到的新规则R′。F0R″进行优化和蕴含处理后，再加入规则集B中，直至规则集B′和规则集B″中的规则不能进行合一化，出现不动点。

步骤4去除规则集B中选择函数不为空的规则，剩下的规则集合就是精简后的逻辑规则集B1。

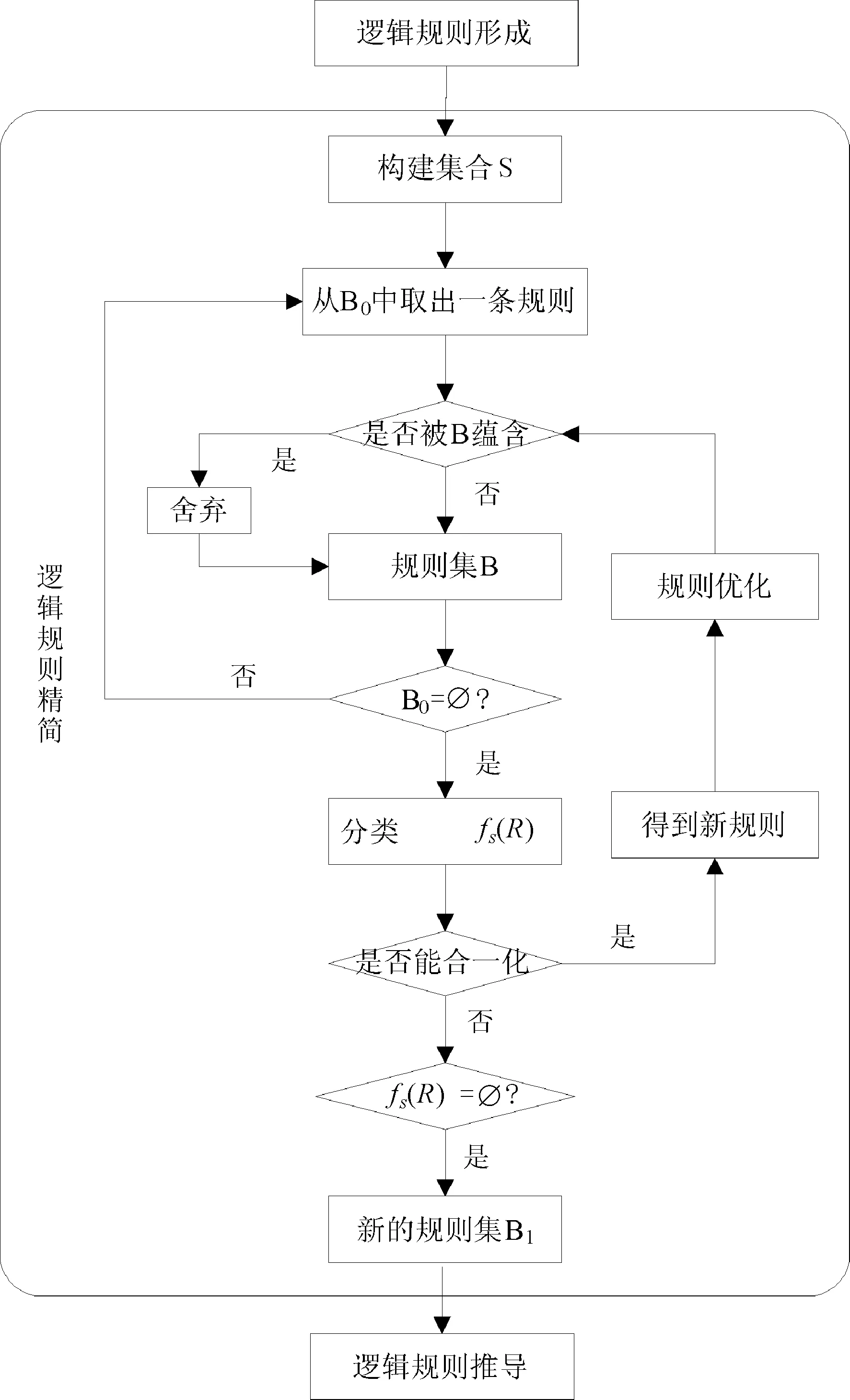
图2　逻辑规则精简流程

3精简集合的等价性证明

依照逻辑规则精简算法得出精简集合B1后，还需证明它与初始规则集B0的推理等价性。

定理1若B1是逻辑规则精简算法得出的逻辑规则集，则B1与初始规则集B0具有等价的推导能力。

证明假设事实F可从规则集B0推导得到，则关于B0存在一个逻辑推导树D0,由它可推导出F。若B1与B0具有等价的推导能力，则事实F也可从规则集B1中的规则推导得到，即关于B1也存在一个逻辑推导树，能推导出F。

根据算法的步骤1可知，除去被规则集B蕴含的规则，B0中其他规则都被加入了规则集B中，所以模块处理结束时，规则集B0中所有的规则都被规则集B的某一规则所蕴含。根据性质1，标记逻辑树D0节点的所有规则都可以用B中的规则来代替，则关于B存在一个逻辑推导树D可推导出F。

若逻辑树D中存在标记节点的规则不在B1中，进行如下转换。假设标记节点η′的规则R′不在B1中，且η′是D中最低的节点，则标记η′所有子节点的规则都在B1中。因R′∉B1，故fS(R′)≠∅。假设F0∈fS(R′)，根据性质2，如果节点η′存在一个子节点η，被标记为R，则可定义R。F0R′,从而可用标记为R。F0R′的节点η″代替节点η和η′。由于η′的所有子节点都被B1中的规则R标记，则fS(R)=∅。由步骤3可知，由B中规则合一化所得的规则R。F0R′除了被规则集B蕴含的，都加入了规则集B中，所以规则合一化所得的规则都被规则集B的某一规则R″所蕴含。根据性质1，可将节点η″标记为R″。由于节点η″代替了节点η和η′，所以逻辑树节点的总数将减少，即关于B存在一个逻辑树D′可推导出F，其节点总数有所减少。

由于在规则进行合一化处理时，需要满足

fS(R)=∅,fS(R′)≠∅,

故在实际应用中，一般每次验证时只关注协议的个别安全属性，经过蕴含去除和优化后，S不仅是有限集，而且只有很少几个逻辑事实。

经过有限次蕴含去除和优化迭代后，标记逻辑树节点的所有规则都属于规则集B1，从而得到关于B1的一个逻辑推导树可推导出F。

4结语

引入基于攻击者能力和先验知识的事实集合S,对表述协议及其安全属性的初始规则集合B0进行精简，可得具有等价推导能力的规则集合B1。由于B1中规则的假设都属于S，而实际应用中S很小，所以，精简算法可提高推导效率，改善推理算法的收敛性。

参考文献

[1]ABADIM,TUTTLEMR.ASemanticsforaLogicofAuthentication[C]//PODC’91ProceedingsoftheTenthAnnualACMSymposiumonPrinciplesofDistributedComputing.NewYork:ACM, 1991: 201-216.DOI:10.1145/112600.112618.

[2]MEADOWSC.TheNRLProtocolAnalyzer:AnOverview[J].JournalofLogicProgramming, 1996, 26(2): 113-131.DOI:10.1016/0743-1066(95)00095-X.

[3]SONGXD,BEREZINS,PERRIGA.Athena：anovelapproachtoefficientautomaticsecurityprotocolanalysis[J].JournalofComputerSecurity, 2001, 9(1/2): 47-74.

[4]潘进,顾香,王小明.基于应用Pi演算的WTLS握手协议建模与分析[J/OL].西安邮电大学学报, 2015, 20(2):26-31[2015-10-20].http://www.cnki.com.cn/Article/CJFDTotal-XAYD201502007.htm.DOI:10.13682/j-issn.2095-6533.2015.02.006.

[5]徐军.关于秘密共享方案在应用Pi演算中的实现[J/OL].计算机应用.2013.33(11):3247-3251[2015-10-20].http://www.cnki.com.cn/Article/CJFDTotal-JSJY201311062.htm.DOI:10.11772/j.issn.1001-9081.2013.11.3247.

[6]李梦君.安全协议形式化验证技术的研究与实现[D].长沙:国防科技大学,2005:93-105.

[7]周倜.复杂安全协议的建模与验证[D].长沙:国防科技大学,2008:95-113.

[8]刘学锋,石昊,苏薛锐,等.安全协议自动验证工具的状态空间剪枝[J/OL].计算机应用,2004, 24(8):117-121[2015-10-20].http://d.wanfangdata.com.cn/Periodical/jsjyy200408037.

[9]石昊苏,薛锐,冯登国.AVSP算法[J/OL].计算机工程与设计,2005,26(4):867-869[2015-10-20].http://www.cnki.com.cn/Article/CJFDTotal-SJSJ200504008.htm.

[责任编辑:瑞金]

Logicalrulessimplificationfortheformalanalysisofcryptographicprotocols

PANJin1,WANGXiaoming2,XIEQingsong1

(1.DepartmentofInformationSecurity,Xi’anCommunicationsInstitute,Xi’an710106China；2.Teamof12th,Xi’anCommunicationsInstitute,Xi’an710106China)

Abstract:Aiming to solve the problem that the initial rule set in the formal analysis of cryptographic protocols is too large to converge, a new method is put forward to streamline the logical rules based on prior knowledge. Using equivalent logic tree theory, the rule set can be implicated and unified in initial rule iteration process, which makes the new logical rule set have the same capacity as the initial one that has not been deflated.

Keywords:formal verification tools, initial rules sets, implication rule, rule of the unifying

doi:10.13682/j.issn.2095-6533.2016.02.003

收稿日期：2015-11-30

基金项目：国家自然科学基金资助项目(61305083)

作者简介：潘 进(1959-)，男，博士，教授，博导，从事网络安全研究。E-mail:2373242787@qq.com 王小明(1982-)，男，硕士研究生，研究方向为网络安全与防护。E-mail:279804359@qq.com

中图分类号：TP393

文献标识码：A

文章编号：2095-6533(2016)02-0016-04