基于有限元分析的电缆中间接头电阻研究

刘国建，肖　礼，代宪亚

(上海电力学院 自动化工程学院，上海　200090)

基于有限元分析的电缆中间接头电阻研究

刘国建，肖礼，代宪亚

(上海电力学院 自动化工程学院，上海200090)

摘要：针对10 kV电力电缆中间接头运行时，电缆芯与连接管处的接触电阻在大电流作用下产生的热量是否为中间接头发生过热现象的最大诱因展开研究。利用有限元分析软件ANSYS对建立的中间接头连接管与电缆芯实体模型进行应力分析。在连接管外表施加冲压(强)后，得到连接管内部应力分布与形变图，读取接触处的仿真压强值，通过换算以及参考接触电阻的工程计算公式，计算出冲压操作产生的接触电阻大小。得出电缆中间接头处接触电阻远小于连接管位置本体电阻，不足以对电缆中间接头造成过热影响的结论，对进一步探究电缆中间接头发热机理具有一定的参考意义。

关键词：电缆中间接头；有限元分析；应力分析；接触电阻

根据国家电力安全事故通报：调研全国重要城市电力电缆运行故障情况时发现，在电缆投入运行25年内，电缆附件的故障率一直是最高的[1]。电力电缆中间接头作为电力电缆附件的一种，因其数量众多、制作要求高[2]，其故障率一直居高不下。调查表明中间接头发生故障的主要原因是接头部分温升过大，因此开展对电力电缆中间接头发热机理的研究具有非常重要的意义。

研究表明，电缆中间接头易产生过热原因有：①结构复杂，内部半导电带、绝缘橡胶、密封胶等虽能保护中间接头避免外部电磁干扰与腐蚀，但也阻止了内部产热向外散热的途径；②电缆接头为两段不同电缆连接处，接触不良或者弯曲容易产生较大的接触电阻，在大电流作用下容易发热。

目前，对电接触电阻的研究已经拓展到各领域。文献[3]提出, 总接触电阻应是所有实际接触点电阻的并联值(称为自身电阻)与因相互影响而造成的电阻值(称为相互电阻)相串联，称之为霍姆电接触模型。这与文献[4]在1951年通过对某一密集点群做繁荣估算得出的结果基本一致。后来，随着计算机科学的发展，越来越多的学者将传统计算与计算机数值仿真结合在一起，构建了不同的接触电阻的计算仿真模型[5-6]。含膜触头静态接触下的接触电阻[7]也在20世纪末被研究。对于接触电阻的实际测量，可以采用欧姆定律。将一段完整导体通以固定电流，一定长度导体的自身电阻为两端电势差与该固定电流比值；若该导体不完整，中间有接触点，用同样的方法，得到第二次计算值与第一次计算值的差值即为接触电阻阻值大小。工程上通常运用实际测量的方式，方便准确。

本文采用一种新的方法研究电缆中间接头位置的接触电阻。在研究电缆中间接头发热机理的过程中，最初认为中间接头部位存在较大的接触电阻，在强电流作用下会是接头发热的主要诱因，经过本文研究论证该观点的错误性。利用ANSYS软件对接头连接管与电缆芯连接处进行应力分析，再结合接触电阻计算公式，对接头接触电阻与连接管位置导体本身电阻进行大小比较，从而得出两种电阻对中间接头发热影响的大小。

1电缆中间接头结构

电缆铺设好后，因单条电缆长度有限，需用连接点将各段电缆连接成连续的线路，成为一个整体，这些连接点就称为电缆接头。中间接头是位于中间部位的电缆接头，终端头是位于线路两端的电缆接头。电缆接头用于保护和固定进出线，对中间处施加防水、防尘、防震动、防干扰等保护之用。电缆中间接头示意图见图1。

图1　电缆中间接头总体示意图

对于电力电缆中间接头部分，存在这样的电接触：电缆芯与连接管之间的电接触，连接管一般为铜，电缆芯材料为铜或铝，经过砂纸打磨，已除去氧化层。根据中间接头的制作与安装工艺，采用冲压方式对连接管与内部电缆进行压合，如图2所示。两侧电缆芯之间不直接接触。本文以一种10 kV电缆中间接头作为研究对象，中间接头结构、尺寸及材料导热系数值如表1所示[8]。

图2　电缆中间接头压接示意图

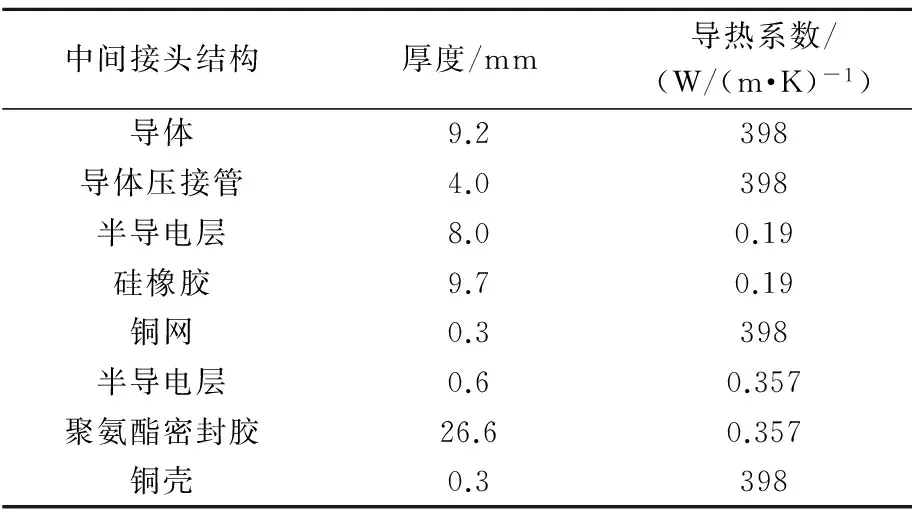
中间接头结构厚度/mm导热系数/(W/(m·K)-1)导体9.2398导体压接管4.0398半导电层8.00.19硅橡胶9.70.19铜网0.3398半导电层0.60.357聚氨酯密封胶26.60.357铜壳0.3398

2电阻

2.1接触电阻

接触的导体通电之后，在电流的作用下，会产生电压降，说明接触中间有电阻存在，称为接触电阻。而其实际产生原理还要从微观角度进行解释：导体末端在微观层次上是粗糙的，有许多小“凸起”，当两个导体末端接触时就会形成小接触点，如图3所示。因此，我们可以把两导体末端的整个接触面看成若干个小接触点组成的集合。研究表明[9]，接触电阻是由膜电阻和收缩电阻组成的。由于工程安装中会对暴露过的导体进行砂纸打磨等操作，因此由金属氧化产生的膜电阻可以忽略不计。收缩电阻是由电流收缩作用引起的。

图3　接触面示意图

文献[10]推导出了被广泛认可的一个接触点的收缩电阻公式：

(1)

式中ρ1，ρ2——接触材料电阻率；a——接触点半径。

若接触面是由个接触点组成，接触电阻可近似看成相互并联[11]，则n个接触点的收缩电阻为：

(2)

但实际中，由于计算导电斑点数n和平均半径α非常困难，工程上常采用经验公式[9]计算：

(3)

式中Rj——接触电阻，mΩ；F——接触压力，N；m——与接触形式、压力范围和实际接触点的数。

实验证明[12]，对于点接触时取m=0.5，线接触时取m=0.5～0.8，面接触时取m=1；kj为与接触材料、表面状况等有关的系数，其值由实验确定(见表2)。

由式(3)可知，接触压力F对接触电阻Rj有重要影响。微观原理如下：当增大接触压力F，超过材料能承受的弹性形变极限后，塑性形变随即发生，材料将不再复原，这时接触面大大增加，接触点也增加，即接触的越好，收缩电阻Rj越小。此外，增大接触压力F会损坏接触处金属氧化层，加大金属接触面，使膜电阻减小。所以增大接触压力F，可以使接触电阻Rj减小。

表2　各种触头材料的kj值

2.2电阻与温度

金属电阻率会随着温度升高而升高。通常认为，温度升高会使金属电子移动的热运动加速，从而增加金属导电性，降低金属电阻。而事实上，温度对电子移动速度和有效电子数量几乎没有影响，但温度升高会加剧晶格振动，会增加偏离平衡位置的原子数量，进而减小了电子运动运程，使电阻率增大。德拜理论阐明，在较高温度时，金属电阻率随着温度线性增加。

对于接触电阻而言，接触处温度升高会使材料的硬度相应下降，在接触力不变的情况下，接触点增加，使有效接触面积增大。电阻率的些微升高使接触电阻增大，但接触面积增大又会使接触电阻减小，此消彼长，所以接触电阻变化甚微。

对于常用的金属而言，本文研究其导电性能与温度的关系。金属电阻率与温度关系可以表示为：

ρT=ρ20(1+αT)

(4)

式中ρT——金属在℃的电阻率；ρ20——金属在室温20℃时的电阻率；α——温度系数；T——取摄氏温度。对于一般金属，温度系数为正温度系数，即金属电阻率会随着温度升高而升高。

3电接触处应力分析

3.1连接管电接触模型构建

电缆芯与连接管材料都是铜，经过压接，两者间隙很小，分析时建立了两者为一体的ANSYS模型如图4所示，认为连接管与电缆芯没有分开，即圆柱体。文中研究相关位置(接触处)的应力，将圆柱体模型沿底面圆横截面任意直径轴向切，因对称性，选取截面之一进行研究，图5为对研究截面网格划分之后的模型。

图4　连接管与电缆芯整体模型

图5　ANSYS模型网格划分示意图

考虑到对连接管冲压后中间凹陷，两端不发生形变。模型构建时，对模型上、下表面(连接管的两端)施加的载荷为“displacement”，即表面固定，没有任何位移；左侧表面施加同样的“displacement”载荷，即连接管中轴不发生位移；对模型右表面(连接管的外表面)施加的载荷为“pressure”，即冲压。具体如图6所示，上、下、左三侧的三角符号表示施加的固定约束，右侧箭头表示施加压强及方向。

图6　ANSYS模型载荷施加示意图

3.2连接管内应力分析

在某电力公司实际调研后知悉，对于10 kV电缆接头，施加在连接管外部的冲压为45 t；对于220 kV电缆接头，施加在连接管外部的冲压为200 t。通常把气体的压力用“公斤”描述，单位是“kg/cm2”，一公斤压力就是一公斤的力作用在一个平方厘米上。即：

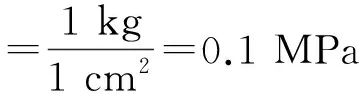
(5)

对于10 kV的电缆接头连接管，外部压强为4 500 MPa。设模型上某一点距离中轴线的垂直长度为d，施加相应载荷之后，可得到连接管内部应力分布图7与内部压强随距离d分布情况图8。根据牛顿第三定律，图8纵坐标数值为负表示与初始施加力方向相反即向外。由图8看出，在电缆芯与连接管接触处——缆芯表面(横坐标0.92)位置，压强约为4 350 MPa。

图7　连接管内部应力分布图

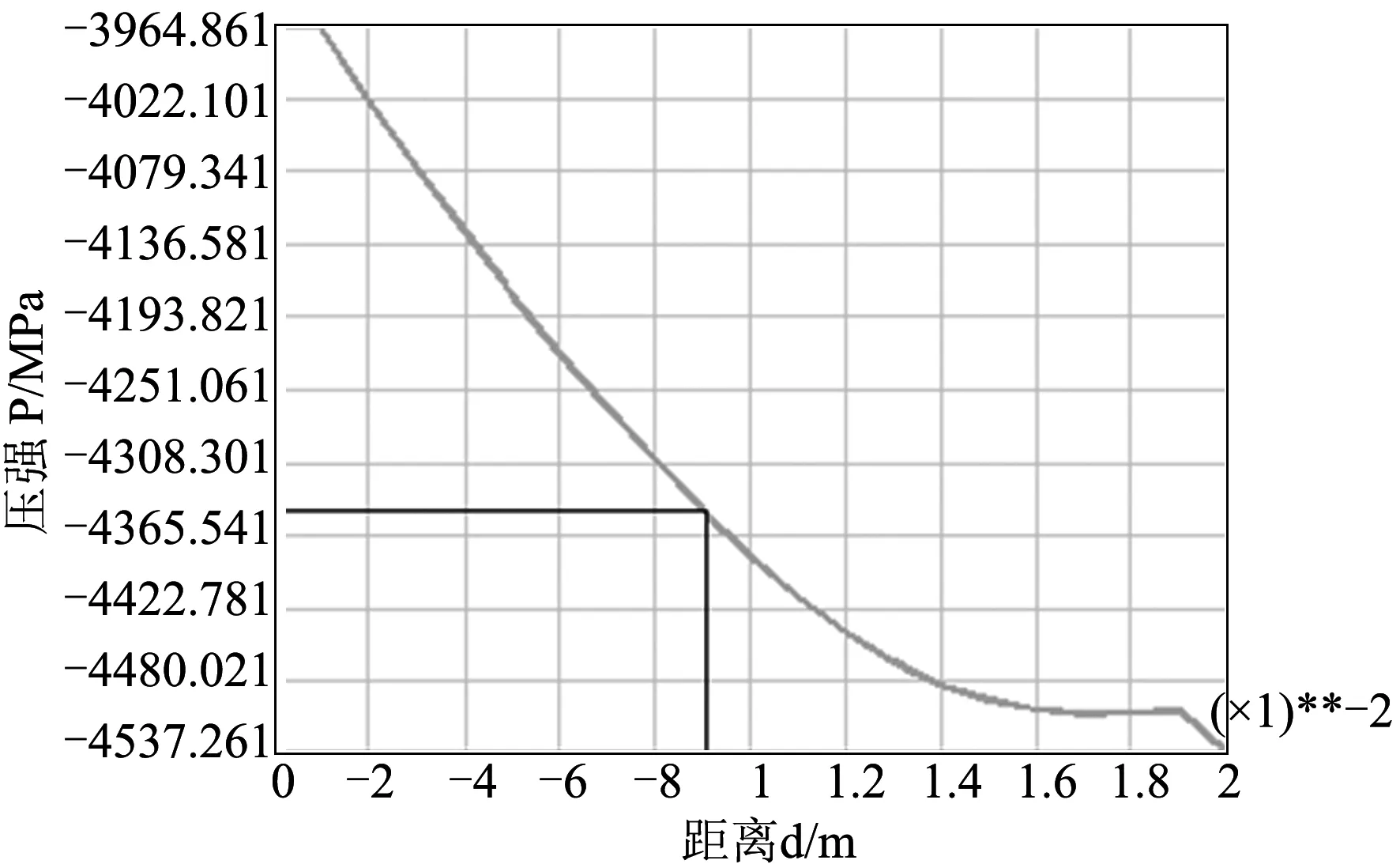
图8　内部压强随d分布情况

3.3电阻比较

(1)接触电阻计算

由本文求得缆芯表面(横坐标0.92)压强约为P=4 350 MPa。现计算接触电阻工程计算公式中值大小：

F=P×S=P×2πr×h

(6)

式中P——压强；S——压强作用面积：h——连接管长度，工程实际中常取0.1 m，此处，r=9.2 mm，由式(6)计算得F=2.5×107N。带入接触电阻的工程计算式(3)，得该电接触的接触电阻Rj=4×10-8Ω。

(2)连接管段导体自身电阻计算

电接触处的电缆芯和连接管是一起通电的，连接管段的导体自身电阻可计算为：

(7)

式中ρ——导体电阻率，20℃时铜的电阻率ρ20=1.75×10-8Ω；l——导体的长度，l=h；S′——电流流经时的横截面积，此处，横截面半径r′=9.2 mm+4 mm，即电缆芯半径与连接管厚度之和。

由式(7)计算可得电阻R=3.2×10-6Ω。若考虑电阻随温度的升高因素，当该部位温度升高时，根据式(4)，铜导体的电阻率会加大，自身电阻也会增大，但接触电阻变化不大。

由比较可得出，Rj=4×10-8Ω<

4结语

本文依托对电缆中间接头发热机理研究，在分析接触电阻产生原因的基础上，利用ANSYS软件对电缆中间接头连接管与电缆芯连接处进行应力分析，然后根据接触电阻的经验公式，验证并说明电缆中间接头处接触电阻与连接管位置导体段本体电阻相比，可以忽略不计。在进行理论分析时，最初认为接触电阻的存在是影响电缆中间接头发热的重要因素，通过实验验证了该想法的错误性。对于进一步探究电力电缆中间接头的发热机理具有重要意义。

参考文献：

[1]罗俊华,杨黎明,姜芸,等.电力电缆运行、故障及试验综述[J]. 电力设备,2004(8):4-8.

LUO Jun-hua, YANG Li-ming, JIANG Yun, et al. Outline of operation and fault and testing for power cable[J]. Electrical Equipment, 2004,5(8):4-8.

[2]江日洪.交联聚乙烯电力电缆线路[M].北京:中国电力出版社,2009.

[3]HOLM R. Electrical Contacts-Theory and Application [M].4th.Berlin: Springer-Verlag, 1967.

[4]TIMOSHENKO S, GOODIER J N. Theory of Elasticity[M].New York: McGraw Hill, 1951.

[5]MALUCCI ROBERT D .Multispot model of contacts based on surface features[J]. The 34th Holm Conference on Electrical Contact, 1988.

[6]GAREN R W. Prediction the contact resistance distribution of electrical contacts by modeling the contact interface[J]. IEEE Trans. on CHMT, 1991, 14 (1)：782-785.

[7]李奎,张冠生,陆俭国. 含膜触头静态接触下接触电阻有限元模型及其分析[J]. 电工技术学报,1998(1):28-32.

LI Kui. The finite-element model and analysis for static contact resistance with film[J]. Transactions of China Electrotechnical Society, 1998(1):28-32.

[8]韩筱慧. 电力电缆中间接头温度在线监测系统的研究[D].北京：华北电力大学,2012.

[9]许军,李坤. 电接触的接触电阻研究[J]. 电工材料,2011(1):10-13.

XU Jun, LI Kun. The research on resistance of electrical contact[J]. Electrical Engineering Materials, 2011(1):10-13.

[10]陈森昌,迟彦惠,张平. 电接触现象和接触电阻模型的研究进展[J]. 广东技术师范学院学报,2015(2):40-44.

CHEN Seng-chang, CHI Yan-hui, ZHANG Ping. Research progress of electrical contact phenomena and contact resistance model[J]．Journal of Guangdong Polytechnic Normal University，2015(2)：40-44．

[11]程礼椿. 论接触电阻模型与应用问题[J]. 高压电器,1993，29(2):34-40.

CHEN Li-chun. On the problems of contact resistance models and their applications in electric contacts[J]. High Voltage Apparatus,1993,29(2):34-40.

[12]程礼椿,李震彪. 接触电阻模型发展与应用[J]. 低压电器,1993(5):10-14.

(本文编辑：杨林青)

Study of Cable Intermediate Joint Resistance Based on Finite Element Analysis

LIU Guo-jian, XIAO Li, DAI Xian-ya

(College of Automation Engineering, Shanghai University of Electric Power, Shanghai 200090, China)

Abstract:This research focuses on whether the heat caused by the contact resistance in cable core and connection pipe under the strong current is the biggest cause for overheat at the intermediate joint during the running process of 10kV cable intermediate joints. The finite element analysis software ANSYS is used to make the stress analysis of the established entity model which contains intermediate joint connection pipe and cable core location. After the force (or pressure) is applied on the surface of connecting tube, the internal stress distribution and deformation map show up; after reading the simulation pressure at the contact, through the conversion as well as the engineering calculation formula of the contact resistance, we can calculate the contact resistance caused by the stamping operation. It is calculated that the contact resistance of the intermediate joint is much less than the body resistance in the connecting pipe position, not sufficient to cause intermediate joint overheating. This research can provide a certain reference value for further exploring the heating mechanism of cable intermediate joint.

Key words:cable intermediate joint; finite element analysis; stress analysis; contact resistance

DOI：10.11973/dlyny201601008

基金项目：上海市“科技创新行动计划”高新技术领域重点科研项目(14511101200)

作者简介：刘国建(1990)，男，硕士研究生，主要从事电力电缆及中间接头发热机理研究。

中图分类号：TM726.4

文献标志码：A

文章编号：2095-1256(2016)01-0037-05

Foundation items：Key High-Tech Project of Shanghai Scientific and Technological Innovation Action Plan (14511101200)

收稿日期：2015-01-11