基于小波变换对信号噪声的处理研究

朱先和，杨世平

(1.贵州大学 大数据与信息工程学院，贵州 贵阳 550025；2.贵州大学 明德学院，贵州 贵阳 550004)

基于小波变换对信号噪声的处理研究

朱先和1，杨世平2

(1.贵州大学 大数据与信息工程学院，贵州 贵阳 550025；2.贵州大学 明德学院，贵州 贵阳 550004)

摘要采用传统的滤波方法对信号进行消噪时，虽然方法简单，但是以牺牲信号的局部特征为代价，且信号的信噪比并未得到有效地改善。文中采用小波变换的方法对信号进行消噪，将原始信号经小波分解后，信号的小波系数大于噪声的小波系数，再选取一合适阈值，保留高于此阈值的信号小波系数，从而达到消噪的目的。实验结果表明，该方法不仅能有效地去除信号中的噪声，且能保留信号的局部特征。

关键词小波变换；消噪；Matlab仿真

在具体的工程问题中，本文所得到的有用信号不可避免的混有一些噪声，其干扰了信号的本质特征，影响了对问题的判断。前人用于消除噪声干扰的主要方法有利用FIR滤波的原理对原始信号进行相对比较平滑的处理，这种方法相对比较简单，但其缺点在于处理后信号的信噪比没有得到较大的改善，并且原始信号的局部特征信息也被模糊了。相比而言，利用小波变换对信号进行消噪时，不仅可较好的改善信号的信噪比，且其能有效的区分信号中的突变部分和噪声，实现对信号的优质消噪。

1小波消噪原理

近年来，小波理论得到了较好的发展。在小波理论的诸多特点中，其多分辨率特点的存在，使其可以很好地表征信号的突变性和非平稳性。另外，小波变换不仅在时域可较好的表征信号的局部特性，且其在频域也可表征信号的局部特征：其在低频部分具有较低的时间分辨率和较高的频率分辨率；在高频部分具有较低的频率分辨率和较高的时间分辨率。综合以上特点可知，小波变换能较好地探测信号中突变部分和反常现象，这也是其能够应用于信号消噪的原因之一[1]。

利用小波变换进行小波去噪的具体过程可以从以下几步来实现，其流程如1所示。

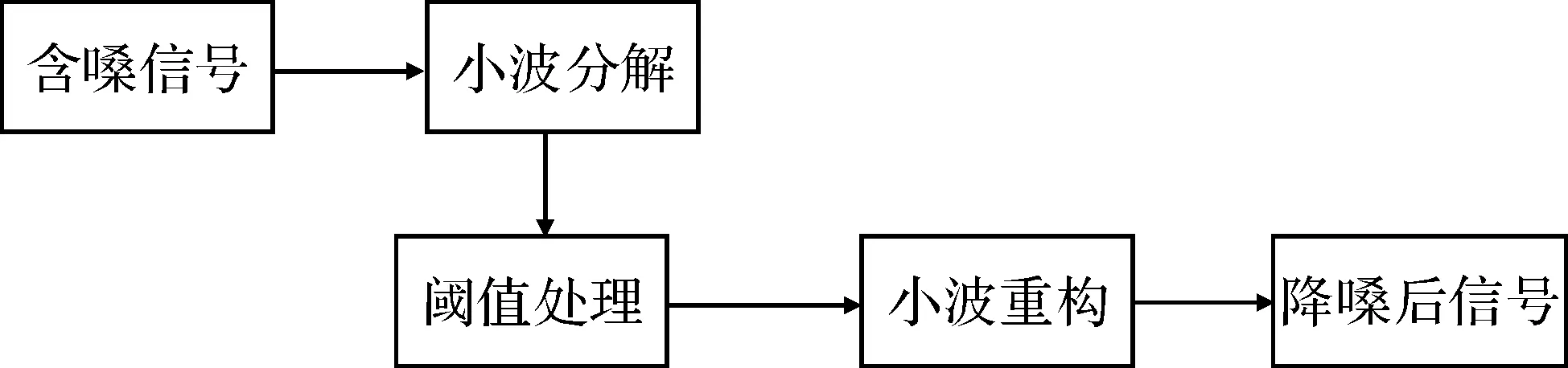
图1　小波去噪流程图

(1)将采集到的原始信号进行小波分解。通过试验选择合适的小波和小波分解层N，将采集到的含噪信号逐一分解，直至分解到到第N层，这样以得到各层的相应小波分解系数，分解过程如图2所示。

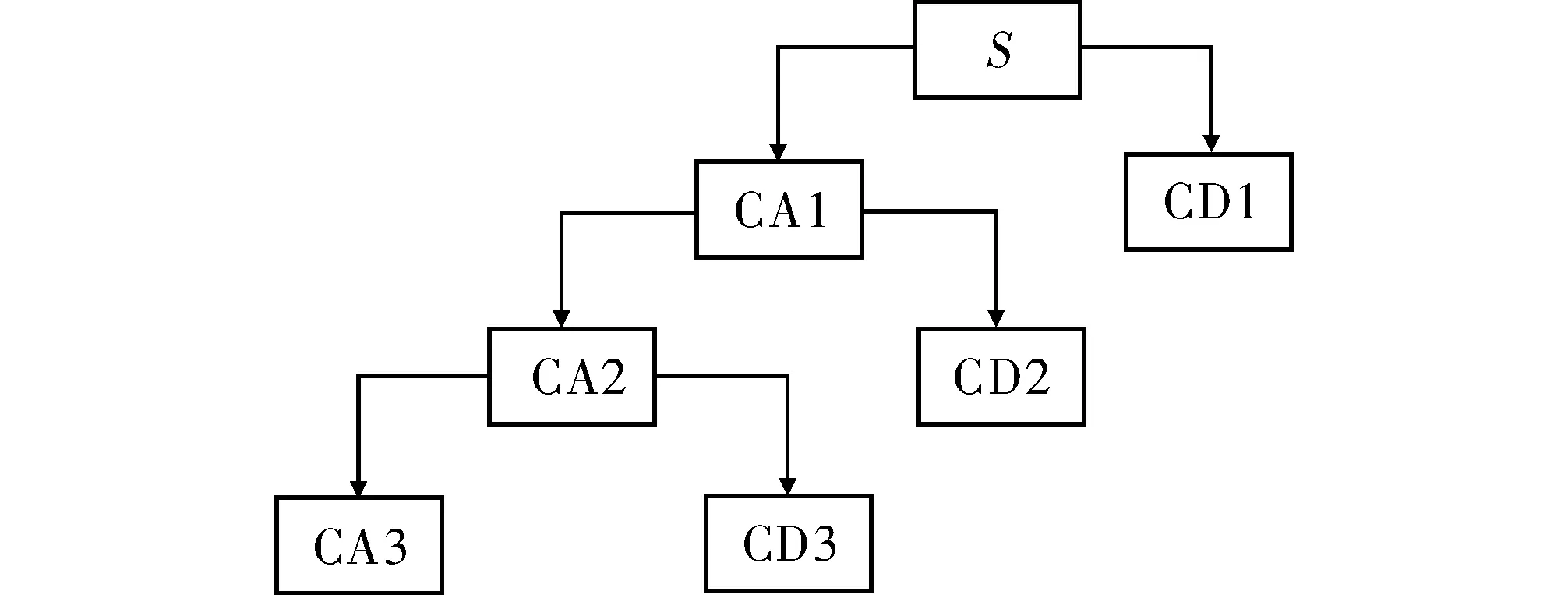
图2　信号的3层小波分解图

(2)对小波分解后的分解系数进行相应处理。对于分解后的每一层，选择一合适的阈值，然后对该层分解系数进行阈值化处理；

(3)信号重构。信号的重构是根据第一步中信号分解的最高层的低频系数和第二步中处理后的一至N层的高频小波系数来实现的。

根据对小波分解后的系数的处理方式不同，小波降噪的方法主要有：(1)模极大值检测法。此方法是由于小波分解后有用信号和噪声的模极大值点表征情况不同，根据这一特性将噪声的模极大值点去除然后重构信号已达到降噪的目的；(2)小波变换阈值法；(3)小波系数相关降噪法，这种方法是先对信号进行小波变换，然后比较相邻尺度小波系数的相关性，根据其不同来区分信号和噪声的小波系数，然后去除噪声的小波系数并重构信号[2]。

相对于其他的小波消噪方法，变换阈值法实现起来比较简单、计算运行速度快，且在分析信号边缘方面优势明显，故其广泛应用于实际工程中。这种方法也是本文的研究重点。

2变换阈值法消噪

变换阈值法消噪的基本原理如下：采集的原始信号在经小波变换后，信号的小波系数要大于噪声的小波系数，根据这一点，文中可选择一个合适的小波系数阈值，将小于此阈值的小波系数归零，保留大于此阈值的小波系数，然后对信号进行重构，如此便可达到降噪的目的[3]。对小波系数的处理和阈值规则的选择成为应用此方法的关键。

2.1小波系数处理的方法

小波系数的处理结果直接影响到信号重构的效果，其处理方法有硬阈值处理法和软阈值处理法[4]。

硬阈值法

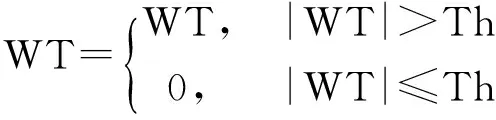
(1)

其中，WT为小波系数；Th为阈值。根据以上定义式可得：硬阈值法就是先将小波变换后的小波系数的绝对值与一阈值相比较，然后将大于此阈值的小波系数保留，而将小于或等于此阈值的小波系数置零。软阈值法

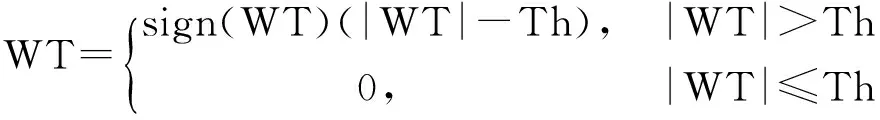
(2)

根据以上定义可得：软阈值法就是先将小波变换后的小波系数的绝对值与一阈值相比较，然后将大于此阈值的小波系数改为此小波系数绝对值与此阈值的差值且其符号保持不变，而将小于或等于此阈值的小波系数置零[5]。

由以上定义可知，软阈值法实现起来比硬阈值法困难，但由于软阈值法处理后的小波谱是连续的，而硬阈值法处理后的小波谱在正负Th处不连续，故用硬阈值法消噪后的信号光滑性没有软阈值法的效果好。

2.2阈值规则的选取

用变换阈值法对信号降噪的关键在于阈值规则选择问题上，这将直接关系到信号消噪的效果。常用的阈值规则有默认阈值规则和自适应阈值规则，默认阈值规则是采用固定的函数来生成信号的默认阈值，而自适应阈值规则则是采用经验公式来得到消噪的阈值。

自适应阈值选择规则主要有以下4种：

(2)Stein无偏风险阈值(Rigrsure规则)。这种规则是一种自适应的选择规则，是基于数学中无偏似然估计所设计的，它是先对一阈值求其似然估计，再将其最小化即得Stein阈值，他是一种估计器；

(3)试探法的Stein无偏风险阈值(Heursure规则)。是通用阈值选择和Stein阈值规则的综合，他也是对变量预测的一种最优选择；

(4)最大最小准则阈值(Minima规则)。这种阈值规则产生的阈值是固定不变的，其产生的极值并不是无误差，而是使其均方误差达到最小值。在应用数学中，这种方法用于估计器的设计。由于经过消噪后的信号类似于数学中估计回归函数的公式，所以在一固定的函数集范围内，可使最大均方误差最小化[6]。

比较以上的几种消噪阈值规则可得知：Sqtwolog和Minimax规则相类似，都是直接将高频系数归零的方法来实现降噪的目的，很显然这种方法比较简单，但其实是以牺牲部分有用信号为代价的，当高频部分所含有用信号较少时，可使用这两种规则；相比较而言，Rigrsure规则和Heursure规则在去噪的同时还能将处在高频的信号较好的保留[7]。

3小波降噪的Matlab仿真实例

3.1一维电压信号实例分析

利用小波分析理论对一含有噪声的一维电压信号作降噪处理，分别运用强制降噪法和默认阈值降噪法，并比较其降噪效果，其中强制消噪法是将小波分解后信号的全部高频系数直接置零来实现消噪的。一维电压信号的处理部分程序如下

load leleccum;

indx=1:1024;

x=leleccum(indx);

%产生含噪信号

init=2055615866;

randn(′seed′,init);

y=x+18*randn(size(x));

subplot(321);

plot(x);

title(′原始信号′);grid;

subplot(322);

plot(y);

title(′含噪信号′);grid;

%用db1小波对原始信号进行2层分解并提取系数

[c,l]=wavedec(y,2,′db1′);

ca2=appcoef(c,l,′db1′,2);

cd2=detcoef(c,l,2);

cd1=detcoef(c,l,1);

%对信号进行强制性消噪处理并图示结果

cdd2=zeros(1,length(cd2));

cdd1=zeros(1,length(cd1));

c1=[ca2 cdd2 cdd1];

s1=waverec(c1,l,′db1′);

subplot(323);

plot(s1);

title(′强制消噪后的信号′);grid;

%用默认阈值对信号进行消噪处理并图示结果

[thr,sorh,keepapp]=ddencmp(′den′,′wv′,y);

s2=wdencmp(′gbl′,c,l,′db1′,2,thr,sorh,keepapp);

subplot(324);

plot(s2);

title(′默认阈值消噪后的信号′);grid;

图3　一维电压信号的小波消噪

从图3中可看出，相比默认阈值降噪处理的结果，用强制降噪法对含噪信号作用后的图形没有那么毛糙[8]，但其代价就是原始信号中的一些局部特征信号不能被保留；而默认阈值消噪后的信号虽在图形的延展性上不如强制消噪的效果好，但其在消噪和保留原始信号特征两者之间平衡的较好，其在消噪的同时最大限度地保留了原始信号的特征。

3.2心电信号的小波去噪

心电信号作为一种生物电信号，其在医学上的应用历史悠久，其主要应用是对心脏的健康状况作出评估。但由于人体的生理系统非常复杂，且心电信号的能量较弱，使得在对其采集时易受到人体其他的生物电信号的干扰，所以有必要对采集到的原始心电信号作消噪处理。据前人研究，常规的滤波技术不能够对心电信号进行消噪，相比而言，采用小波分析能够很好的对心电信号中的噪声作处理[9]。

本文所使用的原始心电信号来自于MIT-BIH数据库，MIT-BIH在医学上是一个权威数据库，现在所被世人所认可的此类数据库有3个：MIT-BIH 数据库、 AHA数据库和AT-T心电数据库，在这3个数据库中，MIT-BIH 数据库被人们的接收度最高，在实验和应用中应用最多。

利用小波分析的理论对原始含噪心电信号进行降噪处理，其Matlab的处理部分源程序如下

a=data;

x=a(1:800,1);

%取采样信号1至800个采样点

subplot(2,1,1); %对图像进行布局

plot(x); %绘制原始心电图像

title(′原始信号′);

%使用默认阈值对信号进行消噪处理

[c,l]=wavedec(x,3,′db1′);

[thr,sorh,keepapp]=ddencmp(′den′,′wv′,x);

y=wdencmp(′gbl′,c,l,′db1′,3,thr,sorh,keepapp);

subplot(2,1,2);

plot(y);

title(′默认阈值消噪后的信号′);

图4　心电信号的小波消噪

由图4可看出，利用小波分析可较好的对心电信号进行消噪，对比强制消噪后的信号和默认阈值消噪的信号，可发现默认阈值法处理后的信号在保留原始信号特征和消噪之间平衡的较好。

4结束语

传统利用滤波进行消噪的方法的应用领域比较局限，其一般只对信号中所含的平稳白噪声和那些含突变部分少的信号有作用，且其去噪的效果不尽人意。相比较而言，利用小波理论对信号进行降噪处理的应用要更广，其能够在对信号进行降噪的同时保留信号的一些有用局部特征、有着更好的适用性，这使得小波去噪在实际工程应用中做了贡献[10]。

虽小波理论得到了较好的发展，但在其应用中还面临着一些问题，例如多维小波和向量小波的发展不够完善、小波基的选取问题、多维小波理论发展不成熟问题和专业性小波分析软件缺乏等问题。这些均有待进一步的研究。

参考文献

[1]Donoho D L,Johnstone I M.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika,1994,81(3):425-455.

[2]Donoho D L,De-noising by soft thresholding[J].IEEE Transcations on Information Theory,1995,41(3):613-627.

[3]Donoho D L,Johnstone I M.Adaptation to unknown Smoothness via wavelet shrinkage[J].Journal of the American Statistical Association,1995,90(12):1200-1224.

[4]Rioul O,Vetterli M.Wavelets and signal processing[J]. IEEE Signal Processing Magzine，1991,10, 8(4):14-38.

[5]Mallat S.A theory for multi-resolution signal decomposition:the wavelet representation[J].IEEE Transactions on PAMI,1989,11(7):674-693.

[6]朱希安,金声震,宁书年,等.小波分析的应用现状及展望[J].煤田地质与勘探,2003,31(2):51-55.

[7]张恒.基于Matlab的小波消噪技术仿真与实现[J].中国西部科技,2010(29):4-5.

[8]徐健,陈士豪.小波分析在图像降噪中的应用[J].电子设计工程,2015,23(1):185-187.

[9]赵国良,杨俊春,孙珅.心电信号的小波变换消噪方法[J].哈尔滨工程大学学报,2004,25(5):631-634.

[10]刘时华,张亚.基于小波分析对信号噪声的处理及应用[J].机械工程与自动化,2015(1):84-85,88.

Signal De-noising Research Based on Wavelet Transform

ZHU Xianhe1，YANG Shiping2

(1.School of Big Date and Information Engineering,Guizhou University, Guiyang 550025, China;2.School of Mingde,Guizhou University,Guiyang 550004, China)

AbstractThe problem of signal de-noising has been concerned by people，When using traditional filtering methods to signal de-noising，Although the method is simple，this is based on sacrifice signal local features for price，and did not get a better SNR. In this paper，The thought of wavelet transform be used for signal de-noising，After the original signal be decomposed，the wavelet coefficients of signals are greater than noise，select an appropriate threshold，and reserved the signal wavelet coefficients which great than the threshold，then will achieve the purpose of de-noising. Experimental results show that this method can not only de-noising effectively，but also to preserve the local features of the signal.

Keywordswavelet transform; de-noising; Matlab simulation

收稿日期:2015-10-27

作者简介:朱先和(1990-)，男，硕士研究生。研究方向：信息安全。

doi:10.16180/j.cnki.issn1007-7820.2016.06.037

中图分类号TN911.7

文献标识码A

文章编号1007-7820(2016)06-128-04