基于并行前缀结构的十进制加法器设计

王书敏，崔晓平

(南京航空航天大学 电子信息工程学院，江苏 南京 211100)

基于并行前缀结构的十进制加法器设计

王书敏，崔晓平

(南京航空航天大学 电子信息工程学院，江苏 南京 211100)

摘要针对硬件实现BCD码十进制加法需要处理无效码的问题，设计了一种基于并行前缀结构的十进制加法器。该十进制加法器依据预先加6，配合二进制加法求中间和，然后再减6修正的算法，并将减6修正步骤整合到重新设计的减6修正进位选择加法器中，充分利用并行前缀结构大幅提高了电路运算的并行度。采用Verilog HDL对加法器进行实现并利用Design Compiler进行综合，得到设计的32位，64位，128位的十进制加法器的延时分别为0.56 ns，0.61 ns，0.71 ns，面积分别为1 310 μm2，2 681 μm2，5 485 μm2。

关键词十进制加法；并行前缀结构；减6修正进位选择加法器

自从冯·诺依曼体系结构出现之后，二进制一直在计算机算术中占据主导地位，处理器设计人员也一直倾向于采用二进制设计计算机运算电路。但是随着金融以及商业计算等领域的发展，提供硬件以支持十进制运算变得越来越迫切。这是以下几点原因造成的：首先，大多数十进制小数，比如0.2，无法在二进制格式下完全精确表示。其次，商业数据库中所存储的十进制数据多于二进制数据，因此采用二进制电路运算时需要在十进制与二进制之间进行转换，这些进制转换工作需要花费时间[1]。另外，当前的金融计算采用软件模拟十进制运算来处理数据以获得精确的结果，但是软件模拟十进制运算要比硬件进行二进制运算至少慢100倍以上[2]，两者之间性能有较大差距。

加法器是十进制以及二进制算术运算单元中不可缺少的运算电路，因此很多二进制甚至是十进制加法器的实现方法被提出。但十进制加法的研究热度一直无法与二进制加法相比，直到2000年以后十进制加法的研究才逐渐成为国内外关注的热点[1]。国外研究人员对BCD码十进制加法做了大量的研究工作[2-11]，在设计十进制加法器时采用8421-BCD码对十进制操作数进行编码。本文根据BCD码加法中预先加6修正，配合二进制加法求中间和，然后再次减6修正的算法设计了基于并行前缀结构的十进制加法器[1]。实验表明，本文设计的十进制加法器能像二进制加法器一样高效地完成加法运算。

1BCD码十进制加法算法

本文设计的十进制加法器采用8421-BCD码对d位(4dbit)十进制操作数A,B进行编码，具体形式如式(1)所示

(1)

其中，Ai∈[0,9]是十进制操作数A的第i个十进制位；aj[j]∈[0,2]是Ai的8421-BCD编码的第j个bit。操作数B的编码方式与A一致。

十进制加法中因为需要处理十进制进位而变得复杂。由于8421-BCD码在表示十进制数时有16种组合，其中6种组合(10102～11112)属于无效码，为产生正确的和以及进位，这些无效码需要跳过。解决这一问题的方法是在其中一个操作数A的每个十进制位加上6得到A*，并采用二进制加法将A*和B相加得到中间和，如果中间和的某个十进制位的进位输出为0,则再对中间和的相应十进制位进行减6修正得到最终和。上述算法的实例如图1所示。

图1　BCD十进制加法举例

在图1中，P=66610=0110_0110_01102被加到操作数A上产生一个预操作之后的临时操作数A*。然后对操作A*和B采用二进制加法求和得到未修正的中间和H。C表示每一个十进制位进位输出的情况，中间和H中没有产生十进制进位的十进制位都被减去6(0110)以得到最终和S。

2十进制加法器设计

根据上述介绍的算法可知，设计十进制加法器时需要在进行二进制加法前对操作数A进行预加6操作，二进制加法结束后根据十进制进位情况进行减6修正得到最终和。本文按照二进制加法中性能最为优越的并行前缀进位选择结构来设计十进制加法运算电路，并将减6修正整合到重新设计的十进制减6修正进位选择加法器中以提高电路运算的并行度。

本文设计的十进制加法器需要在二进制加法前对其中一个操作数A进行加6预操作，其电路如图2所示[11]。

图2　加6电路图

经过预加6操作后A*和B按照二进制加法进行运算。二进制并行前缀进位选择加法器中常用的树形前缀单元包括Sklansky(SK)结构、Kogge-Stone(KS)结构和Brent-Kung(BK)结构，其中KS结构为最快的树形结构，本文采用KS树形结构作为前缀运算单元，16位KS结构如图3所示[12-13]。

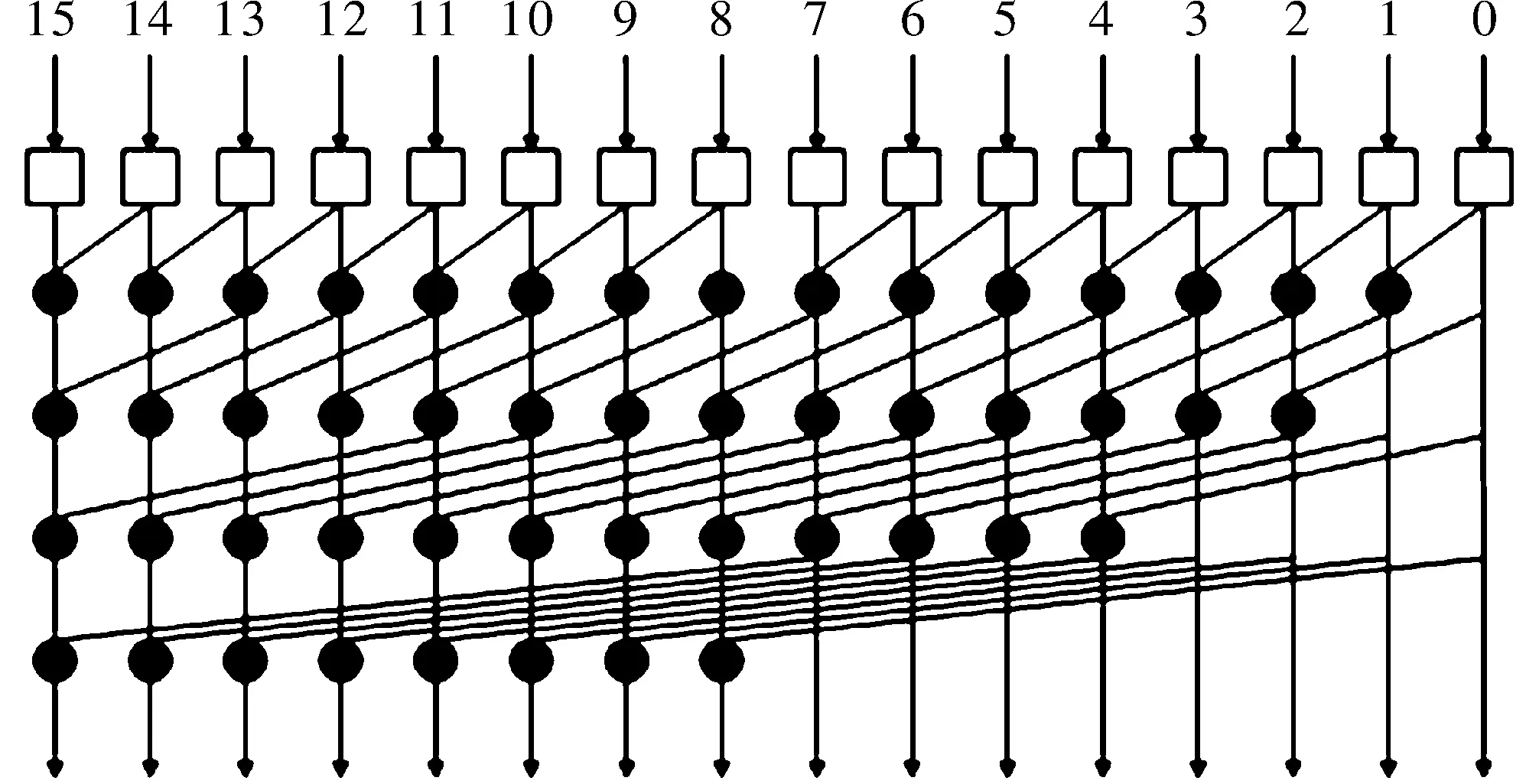
图3　Kogge-Stone树

在二进制并行前缀进位选择加法器中，进位选择加法器为两组进位输入分别为0和1的4位行波进位加法器。进位选择加法器和树形前缀单元并行运算，树形前缀单元输出的进位信号到达后只需经过一个二选一数据选择器就可以得到最终和。在BCD十进制加法中，按照二进制加法得到的是需要减6修正的中间和。本文将减6修正步骤整合到重新设计的进位选择加法中。由上述理论可得，判断中间和的某个十进制位是否要修正的条件是这一十进制位是否有进位输出。如果没有则需要进行减6修正，否则不需要修正。由于在进行二进制加法前有预加6操作，所以中间和中需要修正的十进制位Hi≥6,可以得到如表1所示的真值表。

表1　减6真值表

由表1可以得到从中间和Hi到最终和Si的转换逻辑，如式(2)所示

si[3]=hi[3]·hi[2]·hi[1]；

si[2]=hi[2]⊕hi[1];

(2)

si[0]=hi[0]‘

根据式(2)可知，要将减6修正步骤整合到二进制进位选择加法器中，则需要修改组成二进制进位选择加法器的4位行波进位加法器的电路结构，使其根据最高位全加器的进位输出决定是否进行减6修正，具体电路如图4所示。

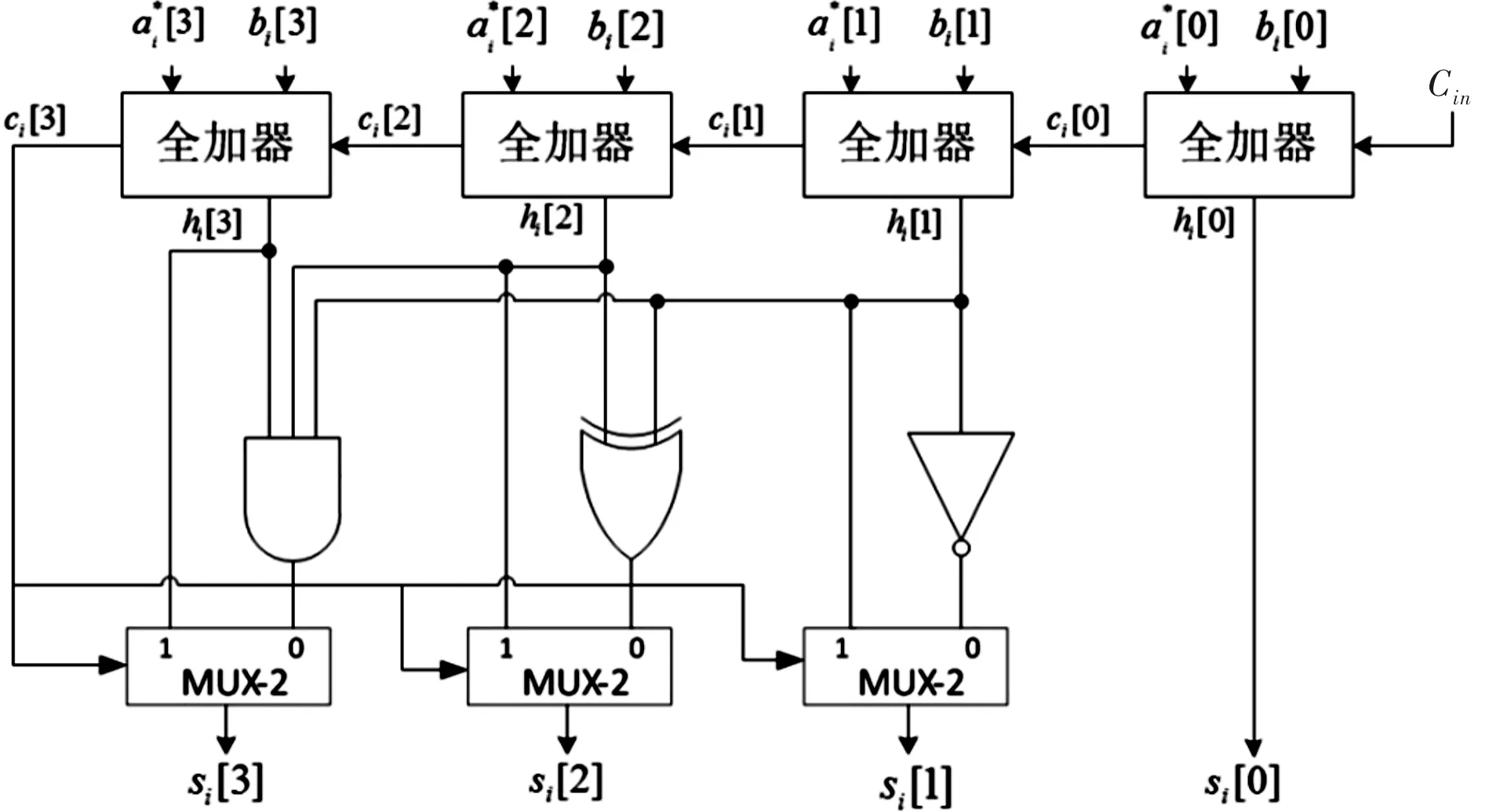
图4　减6修正行波进位加法器

两个如图4所示的减6修正行波进位加法器可以构成一个4位减6修正进位选择加法器，其结构如图5所示。

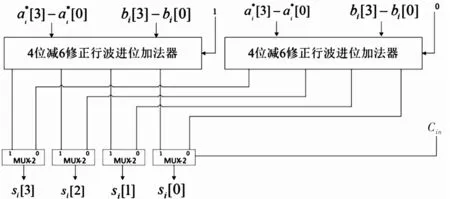
图5　减6修正进位选择加法器

将二进制并行前缀进位选择加法器中的进位选择加法器，替换为图5所示的4位减6修正进位选择加法器，并将经过预加6操作的操作数输入到图3所示的并行前缀单元，即可得到所设计的基于并行前缀进位选择结构的十进制加法器。32位十进制加法器结构如图6所示。

图6　32位基于并行前缀结构的十进制加法器

图6所示32位基于并行前缀进位选择结构的十进制加法器可以拓展为64位，128位十进制加法器，只需要将并行前缀单元改为相应的位宽即可。由此可以得到基于并行前缀进位选择结构的十进制加法器的总体结构如图7所示。

图7　十进制加法器结构图

3实验数据及结果

为获得设计的32位，64位，128位十进制加法器，采用图2所示的预加6操作电路产生 ，并将操作数 和 输入到图7所示的基于并行前缀进位选择结构的十进制加法器中就可以得到十进制和S。减6修正在重新设计的减6修正进位选择加法器中进行，大幅提高电路运算的并行度。使用Verilog HDL语言分别对32位，64位，128位十进制加法器进行描述并在ModelSim平台上进行仿真验证。在Nangate Open Cell 45 nm标准工艺库下，通过Synopsys公司综合工具Design Compiler进行综合，最终得到32位，64位，128位十进制加法器的综合结果如表2所示。

表2　十进制加法器综合结果

4结束语

BCD十进制加法在运算过程中需要解决无效码的问题使得其复杂度远远超过二进制加法。为减少十进制加法的复杂度，本文根据预先加6修正，配合二进制加法，得到中间和后再次减6修正的算法，设计了基于并行前缀结构的十进制加法器。对进位选择加法器重新设计，将减6修正步骤整合到重新设计的减6修正进位选择加法器中，大幅提高了电路运算的并行度。本文设计的十进制加法器借鉴了二进制加法器中性能优越的电路结构，使得十进制加法也能够像二进制加法那样高效的完成。

参考文献

[1]Wang L K, Erle M A, Tsen C, et al. A survey of hardware designs for decimal arithmetic[J]. IBM Journal of Research and Development, 2010, 54(2): 8-22.

[2]Cowlishaw M F. Decimal floating-point: algorism for computers[C]. Santiagode， Compostela：16th IEEE Symposium on Computer Arithmetic, 2003.

[3]Microprocessor Standards Committee of the IEEE Computer Society. IEEE standard for floating-point arithmetic, IEEE Std. 754-2008[S]. America: IEEE,2008.

[4]Schmookler M, Weinberger A. High speed decimal addition[J]. IEEE Transactions on Computers, 1971, 20(8): 862-866.

[5]Hwang I S. High speed binary and decimal arithmetic: U.S. Patent, 4866656[P]. 1989.

[6]Flora L P. Fast BCD/binary adder: U.S. Patent, 5008010[P].1991.

[7]Haller W, Krauch U. Combined binary/decimal adder unit: U.S. Patent, 5928319[P].1999.

[8]Haller W, Li W H. Highly parallel structure for fast multi cycle binary and decimal adder unit: U.S. Patent Application, 20060031279[P]. 2006.

[9]Sacks-Davis R. Applications of redundant number representations to decimal arithmetic[J]. Computer Journal, 1982, 25(4): 471-477.

[10]Shirazi B, Yun D, Zhang C. VLSI designs for redundant binary-coded decimal addition[C]. MA,USA: 7th Annual International Phoenix Conference on Computers and Communications, 1988.

[11]Vázquez A,Antelo E. Conditional speculative decimal addition[C]. HW,USA: 7th Conference on Real Numbers and Computers, 2006.

[12]Mathew S K, Ander M,Krishnamurthy R K, et al. A 4GHz 130nm address generation unit with 32-bit sparse-tree adder core[J]. IEEE Journal of Solid-State Circuits, 2003, 38(5): 689-695.

[13]Dimitrakopoulos G, Nikolos D. High-speed parallel-prefix VLSI ling adders[J]. IEEE Transactions on Computers, 2005, 54(2): 225-231.

Design of Decimal Adder Based on Parallel Prefix Structure

WANG Shumin，CUI Xiaoping

(College of Electronic and Information Engineering, Nanjing University of Aeronautics &Astronautics,Nanjing 210016, China)

AbstractAiming at the problem that the hardware implementation of the BCD code decimal addition requires the processing of invalid code, a new decimal adder based on the parallel prefix structure is designed. The proposed decimal adder based on the algorithm of adding six to each BCD digit of one operand prior to performing binary addition and then subtract six again if a carryout of the digit is not occur. The parallelism of circuit operation is increased by taking the advantage of parallel prefix structure. The designed decimal adder have been realized by Verilog HDL and synthesized by Design Compiler, the delay of decimal adder in 32 bit, 64 bit and 128 bit is 0.56 ns, 0.61 ns and 0.71 ns; the area is 1310 μm2, 2681 μm2 and 5485 μm2 .

Keywordsdecimal addition; parallel prefix structure; carry select adder of subtraction 6

收稿日期:2015-10-19

作者简介:王书敏(1990-)，男，硕士研究生。研究方向:数字系统设计与计算机应用。崔晓平(1962-)，女，副教授，硕士研究生。研究方向：数字系统设计与计算机应用。

doi:10.16180/j.cnki.issn1007-7820.2016.06.006

中图分类号TP332.2+1

文献标识码A

文章编号1007-7820(2016)06-019-04