基于改进PID神经元网络的多变量系统控制算法

宋水泉

(惠州工程技术学校 实训中心，广东 惠州 516001)

基于改进PID神经元网络的多变量系统控制算法

宋水泉

(惠州工程技术学校 实训中心，广东 惠州 516001)

摘要PID神经元网络具有动态特性，在系统控制应用中相比于传统的PID控制方法可取得更优的效果，但其学习算法为梯度学习算法，初始权值随机取得，为了提高其控制量逼近控制目标的速度和系统响应时间，引入粒子群算法对初始权值进行优化，最后应用Matlab软件对改进后的PID神经元网络算法进行仿真。仿真结果表明，该方法具有较好的控制性能。

关键词PID；神经元网络；多变量控制系统；粒子群算法

PID神经元网络是神经元网络与PID控制方法相结合的产物。不同于其他多层前向神经元网络中神经元系统的输入输出特性为静态和相同的特性，PID神经元网络的神经元系统具有动态特性，因此在系统控制应用中相比于传统的PID控制方法可取得更优的效果[1]。但PID神经元网络系统使用的是梯度学习算法，它随机产生初始权值，故在整个学习过程中，存在易陷入局部最优值的问题[2]，这就需要研究优化初始权值的算法以提高PID神经网络算法性能。

1PID神经元网络

从结构角度对PID神经元网络 (Neural Network)进行分析，输入层、隐含层和输出层构成了PID神经元网络的3大部分，其中 个控制量的PID神经元网络由 个相互并列的相同子网络构成，这几个子网络之间是相互独立的，但是也通过网络连接权值进行各自之间的联系。每个子网络的输入层由两个神经元构成，其中一个用来接收控制量的目标量，另一个用来接收控制量的当前值。每个子网络的隐含层是通过比例元、积分元和微分元3大部分组成的，其中比例元对应于PID控制器中的比例控制，积分元对应于积分控制，而微分元对应于微分控制，多个单控制量神经元网络相组合构成了多控制量PID神经元网络[3]。图1所示为多控制量PID神经元网络的拓扑结构图。

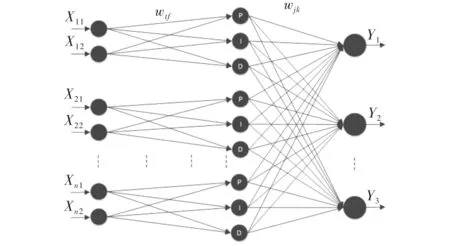
图1　PID神经元网络拓扑图

如图1所示，X11，X21，…，Xn1表示为多控制量神经元网络控制量的控制目标；X12，X22，…，Xn2表示为多控制量神经元网络控制量的当前值；Y1，Y2，…，Yn表示为多控制量神经元网络计算得到的控制律；ωij和ωjk表示为多变量PID神经元网络的网络权值。

PID神经元网络的输入层由2m个神经元构成，输出数据xsi等于输入数据Xsi，计算公式为

xsi(k)=Xsi(k)

(1)

隐含层分别由3m个神经元部分组合而成，分别为m个比例神经元部分、m个积分神经元部分和m个微分神经元部分。这3种类型的神经元的输入值是相同的，其表达形式为

(2)

3种神经元输出的计算公式为：比例神经元

us1(k)=nets1(k)

(3)

积分神经元

us2(k)=nets2(k)+us2(k)+us2(k-1)

(4)

微分神经元

us3(k)=nets3(k)+us2(k)-nets3(k-1)

(5)

输出层是由m个神经元单元组成的，即m维神经元网络输出值，输出层的输出量是根据PID神经元网络的隐含层中全部单元的输出值通过加权和的形式所得到的，其表示形式如下

(6)

受控系统与PID神经元网络控制器相互作用组合可构成一个闭环控制系统，该闭环控制系统可以用图2的形式表示。

图2　PID神经元网络闭环控制系统图

如图2中所示，c1,c2,…,cm为PID神经元网络闭环控制系统中的控制目标；f1,f2,…,fm为PID神经元网络闭环控制系统中的控制器控制律；s1,s2,…,sm为PID神经元网络闭环控制系统中的控制量当前值[4]。

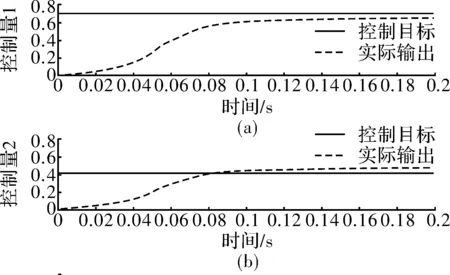
图3　多变量PID神经元网络控制仿真图

应用PID神经元网络控制3变量输入和3变量输出的复杂耦合系统，随机产生PID神经元网络初始权值，PID神经元网络权值学习率为0.045，控制系统的控制间隔为0.001 5 s，控制量1的控制目标为0.7，控制量2的控制目标为0.4，控制量3的控制目标为0.6，应用Matlab软件进行算法仿真，3变量的PID神经元网络控制效果如图3所示，PID神经元控制算法可较好的控制由多变量输入和多变量输出构成的较复杂耦合系统，经过一段时间之后，控制量1、控制量2、控制量3最后接近于设定的目标值。不过，从控制量逼近控制目标速度和系统响应时间角度分析，该控制算法还需要进一步提高效率。由于PID神经元网络采用的是梯度学习算法，因此PID神经元网络初始权值是随机取得的，所以可从优化PID神经元网络初始权值的角度来提高PID神经元网络控制量逼近速度和系统响应时间等特性。

2粒子群算法

为研究优化初始权值的算法以实现提高PID神经网络算法性能的目的，可以在PID神经元网络的基础上增加智能优化算法以改善权值优化搜索的能力。1995年，粒子群算法(PSO)由Eberhart和Kennedy最先提出，其是一种基于种群随机优化技术的先进智能优化算法[5]。

粒子群算法是将待解决的问题进一步转化为在 维解变量空间中对最优位置粒子进行搜索的问题。在N维空间里，粒子 的位置可以用一个矢量来表示，而各个粒子的飞行速度也可用一个矢量来表示。每一个粒子均有相应的适应值，该适应值是由被优化的函数所决定的，每个粒子还具有相应的速度，该速度决定了这些粒子飞行时的距离与方向。通过算法计算，各个粒子能了解自身截止当前可知的最佳位置及当前位置，这些数据作为每个粒子的飞行经验进行进一步的算法使用。与此同时，各个粒子还能了解截止当前所有群体中的粒子可发现的最佳位置，该位置被认为是粒子同伴的经验。群体中的每个粒子便是应用各自经验和粒子同伴中最好的经验进行分析，从而确定下一步所应采取的运动[6]。

最开始时，粒子群算法初始化产生一群随机粒子，紧接着种群中的各个粒子就根据目前为止的最优粒子在解空间中进行搜索，即通过迭代的方式寻求最优解。例如，假定在n维搜索空间中第j个粒子的位置是Xj=(xj,1,xj,2,xj,3,…,xj,n)，第j个粒子的速度是Vj=(vj,1,vj,2,vj,3,…,vj,n)，在进行每次迭代的过程中，粒子通过对两个最优解进行跟踪的方法来更新自己，其中第一个最优解就是粒子自身找到的最优解，即为个体极值pbest，pj=(pj,1pj,2,pj,3,…,pj,n)；另一个就是整个种群截止当前所找到的最优解，即全局最优解gbest。当找到这两个最优值之后，粒子通过以下的两个公式对自身的速度和新的位置进行进一步的计算更新

vj,m(t+1)=wvj,m(t)+c1r1[pj,m-xj,m(t)]+

c2r2[pg,m-xj,m(t)]

(7)

xj,m(t+1)=xj,m(t)+vj,m(t+1),m=1,2,…,n

(8)

其中，w称为惯性权因子；c1和c2称为正的学习因子；r1和r2表示0～1之间均匀分布的随机数[7]。

图4　粒子群算法(PSO)软件流程图

3改进型PID神经元网络

应用粒子群算法优化神经元网络初始权值，粒子群算法(PSO)的初始参数为：种群规模设定为60，进化次数设定为46，同时应用自适应变异的方法来提高全种群的搜索能力，该算法的整个进化过程如图5所示。

图5　粒子群算法进化过程图

将粒子群算法优化得到的最优初始权值引入PID神经元网络，对PID神经元网络的初始权值进行优化，再采用得到的初始权值进行PID神经元网络控制。应用Matlab对该算法进行分析，引入粒子群优化算法的3变量神经元网络控制效果如图6所示。

图6　引入PSO的PID神经元网络算法

由图6中可看出，与图3所示的PID神经元网络算法相比较，经过粒子群算法优化的PID神经元网络控制得到了较好的控制结果，控制量1、控制量2和控制量3能够更加迅速逼近控制目标，同时系统响应时间比原PID神经元网络有所缩短。因此引入优化初始权值粒子群算法的PID神经元网络算法，相比传统的PID神经元网络算法，从控制量逼近控制目标速度和系统响应时间这两个角度看，具有较好的算法性能。

4结束语

由于PID神经元网络的神经元系统具有动态特性，因此其在系统控制应用中，与传统的静态特性的PID控制方法相比较，能得到更加优良的控制效果。但PID神经元网络采用的学习算法是梯度学习算法，初始权值的取得具有随机性，其控制量逼近控制目标速度和系统响应时间等的性能还需进一步提高。所以，需要研究优化初始权值的算法以实现提高PID神经网络算法性能的目的。而粒子群迭代算法可较好的优化PID神经元网络初始权值，从而提高了PID神经元网络中控制量逼近控制目标的速度，减少了系统响应时间。通过Matlab软件进行算法仿真，引入粒子群算法的PID神经元网络算法相比于PID神经元网络具有较好的控制特性。

参考文献

[1]舒怀林.PID神经元网络对强耦合带时延多变量系统的解耦控制[J].控制理论与应用,1998,15(6):920-924.

[2]楚彦君,巨林仓,刘军辉.PID神经网络控制器的设计及仿真研究[J].工业仪表与自动化装置,2004(2):3-6.

[3]程启明,郑勇.球磨机多模型PID型神经元网络控制系统[J].中国电机工程学报,2008,28(2):103-109.

[4]舒怀林.基于PID神经网络的倒立摆控制系统[J].机床与液压,2008,36(3):141-144,146.

[5]蔡琪,单冬红,赵伟艇.改进粒子群算法的云计算环境资源优化调度[J].辽宁工程技术大学学报:自然科学版,2016,35(1):93-95.

[6]刘衍民.粒子群算法的研究及应用[D].济南:山东师范大学,2011.

[7]梁军.粒子群算法在最优化问题中的研究[D].南宁:广西师范大学,2008.

Simulition of Multivariable Control Systems Based on Improved PID Neural Network

SONG Shuiquan

(Training Center, Huizhou Engineering Technical School, Huizhou 516001, China)

AbstractPID neural network has dynamic characteristics, and it can achieve better results than traditional PID control method in system control, but its learning algorithm is a gradient learning algorithm. The initial weights are random obtained. In order to improve the speed and system response time of the control system, we introduce the particle swarm algorithm to optimize the initial weights, and use Matlab software to simulate the improved PID neural network algorithm. The result of simulation reveals that the proposed method is better than traditional PID neural network control performance.

KeywordsPID; neural network; multivariable control systems; swarm optimization algorithm

收稿日期:2015-12-18

作者简介:宋水泉(1981-),男，实验师。研究方向:电气工程及自动化。

doi:10.16180/j.cnki.issn1007-7820.2016.06.008

中图分类号TP183

文献标识码A

文章编号1007-7820(2016)06-026-04