基于结构图设计LDPC码及其性能仿真
2015-04-13张凯杨勇
张凯 杨勇

摘 要: 提出了使用结构图设计列重为3的正则LDPC校验矩阵。所设计出的校验矩阵具有较大的围长,并且可以改变码长和码率。这些码可以很好的使用在通信和数据存储领域。最后对这些设计出的LDPC码进行了计算机仿真,仿真的数据结果表明:设计出的码在加性白高斯噪声信道下比随机产生的LDPC码有着更为优良的性能。
关键词: 正则LDPC码; 校验矩阵; 数据存储; 计算机仿真
中图分类号: TN911.72?34 文献标识码: A 文章编号: 1004?373X(2015)01?0066?03
Abstract: The regular low?density parity?check (LDPC) check matrix with column weight j=3 designed with structure charts is proposed in this paper. The check matrix has large girth, can change code length and code rate. These codes may be used in the fields of communications and data storage. The computer simulation for LDPC codes that the authors designed was performed. The simulation results show that the designed codes have better bit?error?rate decoding performance and lower error floors in additive white Gaussian noise channels than those of LDPC codes generated randomly.
Keywords: regular LDPC code; check matrix; data storage; computer simulation
0 引 言
低密度奇偶校验码(Low?Density Parity?Check codes,简称LDPC码)是一种近年来发现可逼近香农限、纠错性能空前优良的纠错码,该码是Gallager于1962年提出的一种基于稀疏校验矩阵的分组码,亦称Gallager码[1]。由于受当时的计算机仿真水平以及硬件实现能力的局限,LDPC码的优良性能一直未能被真正挖掘,以致被忽视了近40年。近年来,在Turbo码研究获得巨大成功的带动下,Mackay等人又重新研究了LDPC码,发现采用和?积译码算法时[2],其性能十分逼近香农限,在译码复杂度低于Turbo码的同时极具高速译码的潜力等特性,从而激起了人们对LDPC码研究的热潮。LDPC码成为当今信道编码领域最瞩目的热点。
近年来在如何设计出较大围长的LDPC码领域开展了许多研究工作,Kou,Lin,and Fossorier,提出了有限几何的方法构造围长为6的LDPC码[3],Hu等学者在文献[4]中提出了一种基于计算机搜索LDPC码的构造方法,称为渐进增边(Progressive?Edge?Growth,PEG)构造法。近年来又有学者提出了基于有限域构造多元LDPC码的方法[5]。本文提出了利用结构图设计性能优良并且具有较大围长的LDPC码的方法。
1 LDPC码的结构
LDPC码最初是用一个稀疏的校验矩阵来定义的线性分组码,校验矩阵[H]中所有元素值都为二进制数,且每行及每列元素中1的个数远小于码长,因此称之为低密度校验码。LDPC码有两类,一类是正则LDPC码,其校验矩阵中具有相同的行重和列重;另一类是非正则LDPC码,这类码的校验矩阵的行重和列重不尽相同。把一个[(N,K)]-LDPC码定义为一个[M×N]的校验矩阵[H,]其中[K=N-M,]码率为[R=kN;]若[H]为非满秩矩阵,则[K>N-M,]其纠错能力也随之下降。LDPC码的校验矩阵[H]可以用二部图来表示,假设二部图[G]中有[N]个左节点(称为信息节点)和[M]个右节点(称为校验节点),则一个二部图就可以生成一个长为[N,]维数至少为[N-M]的线性分组码。
该码字中的[N]个码字分别表示[N]个信息节点的数值(0或1),则一个码组向量[x=(x1,x2,…,xn)]满足这样一个条件:任一校验节点的相邻信息节点的数值和为0,如图1所示。二部图中的信息节点与校验节点之间的连线称为边(edge)。若第[j]个信息节点与第[i]个校验节点有边相连接,则校验矩阵中的[H(i,j)=1,]否则为0。
2 LDPC码的结构图
构造的LDPC码是基于几何图形的结构图,这里首先给出设计时所要用到的几个定义,将校验节点[Ci(i=1,2,…,M)]作为集合[X,]对于列重为3的LDPC码的校验矩阵每一列都构成了一个由集合[X]中三个非元素组成的列三角,把这些由三角形所构成的图形叫做结构图,如图2所示。
利用结构图可以很容易地判断在LDPC校验矩阵[H]中是否存在短环。围长为4的短环是由在两点间存在两条连接线所构成,围长为6的短环恰好构成了一个三角形。如图2所示,[△C2C4C6] 就构成了一个围长为6的短环。为了将它和列三角区分开来,把类似于[△C2C4C6]的三角形称作循环三角。
图3给出了一些可能存在的情况,在图3中[△abf,][△bcd,][△def]都属于列三角,而[△bdf]属于循环三角,因为[△bdf]的每一条边都和其他的三角形所共用。对于围长为8的LDPC码的结构图也有类似的定义,只是它的短环是由四边形构成的。在这里还要介绍有关斜 度以及可联接斜度的概念。假设把校验点集合[X={a1,a2,…,ap,b1,b2,…,bp,c1,c2,…,cp}]分成三个子集[X0={a1,a2,…,ap},][X1={b1,b2,…,bp}]和[X2={c1,c2,…,cp},]把它们纵向排列,并从下到上依次标明顺序,如图4所示。连接校验点[ai∈X0]和[bj∈X1]之间边的斜度定义为[s=j-i。]在图4中[a1]和[b5]之间的斜度为[s=+4,][b5]和[c4]之间的斜度为[s=-1。]
可联接斜度是指,两条斜度之间有着共同的校验点,这样可以引入第三条斜度从而构成三角形。例如,对于图4中的[a1,b5]、[b5,c4]两条斜度就构成了可联斜度,但是[a1,b5]、[b4,c3]就不能构成可联斜度,因为两条斜度之间没有共同的校验点。把有着共同的校验点的斜度对所构成的集合称为可联接斜度对集合[A。]
3 利用结构图设计LDPC码
为了设计出围长为8的LDPC码,必需排除围长为4和6的短环出现的可能。只要使每一条边属于惟一的一个列三角,那么就可以避免围长为4的短环出现,在结构图中可以很容易的实现。所以现在的问题是如何排除围长为6的短环出现。
假设[c=3p,p]是任意正整数。同样,把这些校验点平均分割成三个子集[X0,][X1]和[X2,]每个子集的元素个数都是[p。]将三个子集的元素纵向排列,并从下到上依次标号(如图4所示)。在构造的过程中,只考虑在不同子集之间出现的边的情况。在这里要引入边集合的概念,边集合[Si]代表了在相邻子集[Xi]和[Xmod(i+1,3)]之间所有的边,可以看出集合[Ai∈Si]。在计算边集合[Si]中每一条边的斜度都是以校验点集合[Xi]中的元素为参考点,可以证明在每一个集合[Si(i=0,1,2)]中的元素个数是相同的。为了避免在列重为3的高码率LDPC码中出现围长为6的短环,就要在校验点集合[Xi]中找到斜度对集合[Ai,]使得尽可能多的构建出列三角,不出现循环三角。
定理1:在结构图中任何列三角或循环三角都是由处在不同集合[Si(i=0,1,2)]中的边所构成,边的斜度分别为[s0,][s1,][s2,]且满足[Mod(s0+s1+s2,p)=0。]
定理2:假设三个斜度对[s0,s1,s2]分别属于集合[A0,][A1,][A2,]且[Mod(s0+s1+s2,p)=0,]那么所有这些斜度对能够构造出[p]个三角形,且任意两个三角形不共享同一条边。
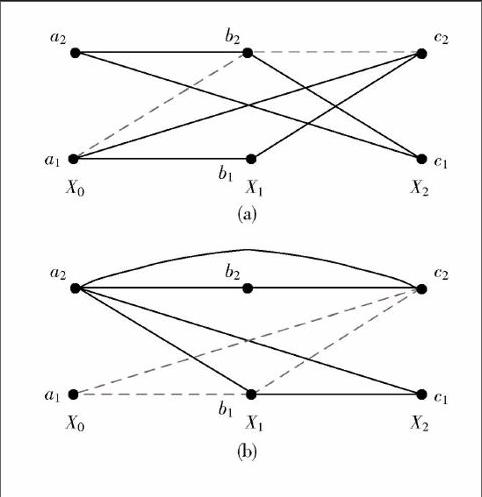
例如,对于[p=2]来说,在引入所有的斜度后只能构成2个三角形,如图5所示。在图5(a)中如果再将点[a1,b2,c2]互相连接构成三角形,那么在[△a1b2c2]与[△a1b1c2]之间有共同边[a1c2,]它将引入围长为4的短环。在图5(b)中如果再将点[a1,b1,c2]互相连接构成三角形,那么新引入的三角形会在结构图上附加[△a2b1c2,]由于附加三角形的存在,它会构成围长为6的短环,因为[△a2b1c2]的三条边分别和另外的3个三角形所共享。
有了以上两条定理和先决条件,现在就可以构造围长为8的LDPC码。定义[B]为所有斜度对集合,并且把[Bi]称作集合[Ai]的候选集。构造过程如下:
(1) 初始化,令[Ai=Φ,i=0,1,2;]
(2) 在候选集[Bi(i=0,1)]中,分别选取一组斜度对[si1,] 令[s21=Mod(-s01-s11,p)]。将[si1]作为集合[Ai]的元素,并且将其从对应的集合[Bi(i=0,1,2)]中删除。设置[k=2;]
(3) 如果[B0]为空,跳转至(9); 否则在候选集[B0]中任意选取[s0k]作为集合[A0]的元素,并且将其从对应的候选集[B0]中删除;
(4) 如果存在某一数值[j][(1≤j≤k-1),]使得[sl∈A2,]则将[s0k]从集合[A0]中删除,跳转至(3)。在这里[sl=][Mod(-s0k-s1j,p);]
(5) 如果[B1]为空,跳转至9; 否则令[B′1=B1;]
(6) 如果[B′1]为空,则从集合[A0]中删除[s0k,]跳转至(3)。否则在[B′1]中任意选取[s1k,]将其作为集合[A1]的元素,并从集合[B′1]中删除;
(7) 如果存在某一数值[j][(1≤j≤k-1)],使得[sl∈A2],则将[s1k]从集合[A1]、[B1]中删除,跳转至(6);
(8) 令[s2k=Mod(-s0k-s1k,p)],如果[s2k∈B2,]则将[s2k]从集合[B2]中删除,并把它作为[A2]的元素,设置[k=k+1,]跳转至(3);否则跳转至(6);
(9) 结束。
集合[Ai]就是我们想要寻找的,它的维数是[Ns=k-1。]在以上的过程中,因为1个列三角是由不同斜度的边所构成,所有斜度构成的列三角数目是[p]个,所以LDPC码的码长就是[n=Ns×p,]码率是[r=Ns×p-3pNs×p=][Ns-3Ns。]如果想要获得不同的码率,可以通过寻找斜度对来改变[Ns]的值。从上述关系可以得到码长和码率之间的关系:[n=3p(1-r),]如图6所示。例如,可以选取[p=77,]通过上述方法,可以得到码长为1 155,码率为0.8的LDPC码。
4 仿真结果与分析
用上述方法构造出LDPC码和用随机方法构造出的等长等码率的LDPC码进行比较,并在加性高斯白噪声(AWGN)信道模型中进行计算机仿真,译码时采用迭代次数为50的和?积算法,调制方式为BPSK,仿真结果如图7所示。
图7中所使用的由两种方法构造出的LDPC具有相同的码长6 690和相同的码率0.9。当信噪比小于4.1 dB时,两种码的性能基本上没有任何区别,但是在信噪比大于4.1 dB时,采用结构图法构造出的LDPC码的优势就逐渐显现出来。可以看到在误码率为[10-6]时,采用结构图法构造出的LDPC码可以获得0.2 dB增益。
5 结 论
本文详细介绍了如何利用结构图来构造列重为3的正则LDPC码。构造出的码具有可变的码率和码长,所以它可以广泛地应用到各种领域,如通信和数据存贮等。在高信噪比条件下,这些由结构图产生的码性能明显地优于随机产生的LDPC码,并且有着更低的错误平层。
参考文献
[1] GALLAGER R G. Low?density parity check codes [M]. Cambridge, MA: MIT Press, 1963.
[2] MACKAY D J C, NEAL R M. Good codes based on very sparse matrices [J]. Lecture Notes in Computer Science, 1995, 1025: 110?111.
[3] KOU Yu, LIN Shu, FOSSORIER M P C. Low?density parity?check codes based on finite geometries [J]. IEEE Transactions on Inform Theory, 2001, 47(7): 2711?2736.
[4] HU X Y, ELEFTHERIOU E, ARNOLD D. Regular and irregular progressive edge?growth tanner graphs [J]. IEEE Transactions on Inform Theory, 2005, 51(1): 386?398.
[5] ZENG LQ, LAN L, TAI YY, et al. Constructions of nonbinary quasi?cyclic LDPC codes: A finite field approach [J]. IEEE Transactions on Commun, 2008, 56(4): 545?554.
