基于小波分析与SVD的机械故障诊断*

李宏亮，黄　民，高　宏，马　超

(北京信息科技大学 机电工程学院，北京　100192)

基于小波分析与SVD的机械故障诊断*

李宏亮，黄民，高宏，马超

(北京信息科技大学 机电工程学院，北京100192)

摘要：对小波变换后相邻两频带内信号存在频率混叠和因采样点数过多导致奇异值分解过程中无法计算或计算时间较长等问题，提出了小波-滑移时间序列奇异值分解方法。通过小波变换，将原始采样信号分解到不同频内。利用滑移时间序列奇异值分解法进一步处理所需频段。通过将所需频段内信号分成若干等长度的子时间序列，依次对其进行奇异值分解，根据奇异值提取需要的特征信息，然后将其拼接成等采样点数的时域信号。利用该方法，对滚动轴承内圈故障的运行声音信号做了处理。从而，验证了方法的可行性。

关键词：小波变换；奇异值分解；滑移时间序列；特征提取

0引言

目前，利用信号分析与处理技术发现机械设备的早期故障及发生故障的原因和部位显得尤为重要。由于机械设备所处工作环境、结构和组成的复杂，采集到的原始信号噪声干扰较多，能够反映机械设备故障信息的有用信号一般都很微弱，被强噪声所淹没，如何对原始信号进行有效降噪、提取微弱特征信号，是能否进行准确诊断的前提。随着小波理论的完善与发展，基于小波变换的微弱特征提取[1-2]和小波阈值降噪法[3-4]被广泛应用，但不同的阈值选取形式直接关系到降噪的优劣[5-6]，而且，经小波分解后不同频段内的信号仍存在着频率混叠现象。近年来，因奇异值分解(singular value decomposition，SVD)降噪法具有零相移、波形失真小、信噪比高等特点，SVD、奇异值差分谱及奇异值与经验模态分解、小波变换和多重分形等融合方法在信号降噪与微弱特征提取领域同样获得了广泛的应用[7-11]。但在进行奇异值分解之前，需要重构吸引子轨迹矩阵A，当信号采样点较多时，吸引子轨迹矩阵A维数较大，使得计算量加大、造成对计算时间长、计算机无法计算等问题。

因此，提出一种基于小波分析与滑移时间序列SVD的机械设备故障诊断方法。首先，通过离散正交小波对原始采样信号进行小波分解并根据小波分解系数对各频段信号进行重构。然后，对不同频段内存在频率混叠的信号进行滑移时间序列奇异值分解处理。经该方法处理后的信号避免了不同频段内存在信号混叠的现象，同时，避免了在奇异值分解过程中因点数太多造成计算机无法计算等问题。

1小波分析

通过对信号采样，可得到一个有限频带的离散信号，分析频率范围为0到fs/2(fs为采样频率)。对信号进行多尺度分解，就是将其分解为两个信号，低频部分和高频部分，根据实际需求，可对低频部分做进一步分解，得到更低频率部分和频率相对较高的部分。如果对信号进行K层分解，则可得到K+1个频段的信号，分解层数K需根据实际情况而定。

设{Xt，t=0，1，…N-1}为取样后的信号，{gl,l=0,1,…L-1}是低通滤波器，{hl,l=0,1,…L-1}是高通滤波器，L表示为滤波器长度。其中，gl与hl满足如下关系：

hl= (-1)lgL-l-1

(1)

或者：

gl= (-1)l+1hL-l-1

(2)

(3)

其中，mod表示两数相除取余，t=0，1，…Nj-1。

信号重构过程是分解的逆过程，其与分解主要不同在于“二抽取”变成了“二插值”，而且是先插值后滤波。但经小波变换后不同频段内的信号仍存在着频率混叠问题。

2奇异值分解

利用采样后的离散时间信号{Xt，t=0，1，…N-1}，构造m ×n维(m≥n)吸引子轨迹矩阵A，则Am×n可表示为：

其中：m+n-1=N；对m×n维矩阵A进行奇异值分解，可得：

A=UΛVT

(4)

式中：U和V分别是m×m和n×n的正交阵，分别是左右奇异值矢量矩阵，Λ为m×n的奇异值矩阵，表示为：

其中，∑=diag[σ1σ2…σr]，r=rankA。σi为矩阵A的奇异值(i=1,2…r)，并满足σ1≥σ2≥…≥σr≥0。

当n越大时，混合信号中各分量奇异值独立分离效果越好[12]，因此，当信号长度N固定时，n的取值为：

(5)

通过正交矩阵U和V的列矢量和奇异值σi，吸引子轨迹矩阵A可表示为：

A=σ1u1v1T+σ2u2v2T+…+σrurvrT

(6)

因此，根据选取不同正交矩阵U和V的列矢量和奇异值σi，便可构造出不同的特性信号。但当采样后的信号点数较多时，构造出的吸引子轨迹矩阵A维数较大，给计算带来困难，为使计算方便，提出滑移时间序列方式进行奇异值分解。

3小波-滑移时间序列SVD算法

小波-滑移时间序列SVD算法如图1所示。

图1　小波-滑移时间序列SVD算法

首先通过小波变换将原始信号分解成等长度低频近似信号和高频细节信号后，但经小波变换后的信号存在着相邻频段内频率混叠现象，为消除该现象，以提高故障诊断的准确性，需对各信号进行奇异值分解，但因原始信号点数过多，导致计算量较大，对所需频段内信号进行了等间隔划分，划分所需步长依实际情况、硬件设备所决定。对划分后各子时间序列进行奇异值分解，通过选择各子时间序列分解结果获得的不同奇异值和左、右正交矩阵的列矢量提取不同的特征信号，该特征信号认为时域信号，其长度与原划分子时间序列长度相等。考虑到频域分析内频率分辨率等因素，将各子时间序列奇异值分解后提取出的特征信号进行重新拼接，得到与原始信号等采样点数的时域信号，通过对其作进一步分析，提高机械设备故障诊断的准确性。

4工程应用

利用声学传感器采集圆柱滚子轴承(N1004)运行过程中的声音信号，采样频率51.2kHz，采样时间2s。测量时，外圈不动，通过螺栓径向加载，内圈转速为493r/min。其时域信号如图2所示。

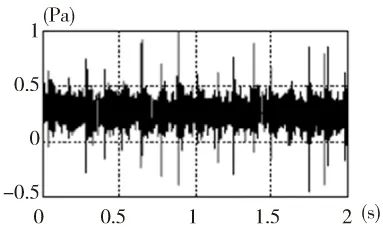
图2　原始采样信号

当滚动轴承内圈、外圈或滚动体存在故障时，其时域信号往往会产生周期性的脉冲冲击、调制等现象。根据图2所示的原始时域信号可知，时域信号中存在着明显的脉冲冲击信号，由此推断该轴承可能存在着故障，为进一步判断其是否存在故障及存在故障的类型采用了小波-滑移时间序列SVD算法。

采用db5小波对原始采样信号进行4个尺度的小波分解与重构，得到不同频带的时域信号，如图3所示。

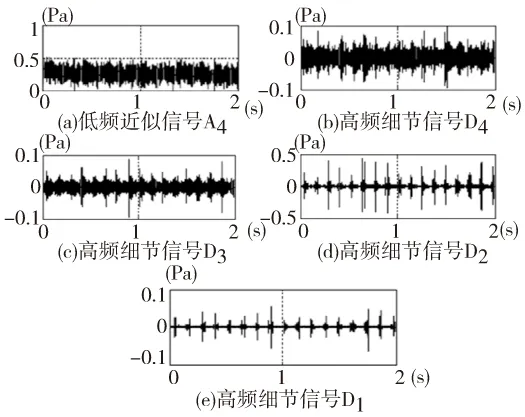
图3　小波变换后各频段时域信号

其中，图3a为低频近似信号，图3b为第4个尺度下的高频细节信号，图3c为第3个尺度下的高频细节信号，图3d为第2个尺度下的高频细节信号，图3e为第1个尺度下的高频细节信号。对不同尺度下时域信号进行频谱分析，其谱图如图4所示。

图4　小波变换后各频段时域信号频谱图

由图4可知，经小波变换后原始信号虽然分解到了各不同频段内，但相邻两个频段内信号仍存在着频率混叠现象，其中，除高频细节信号D3能量较分散外，其他频段能量较为集中。由图4d可知，高频细节信号D2的能量主要集中在约11kHz处，对其进行包络解调处理。其包络谱如图5所示。

图5　高频细节信号D2包络谱

其中，标有“*”处对应的频率分别是43、51.5、58.5、68和117Hz。该滚动轴承(N1004)内圈故障特征频率为7.06fr，fr为转频。因此，内圈故障特征频率为58.05Hz。因包络谱特征频率为58.5Hz，与内圈故障特征频率接近，由此可断定该轴承内圈出现了故障。该判断结果与实际情况相符，在实验前，人为对该轴承的内圈进行了破坏。但是，在约14kHz频率处，明显出现了与下一频段频率混叠的现象，对高频细节信号D2进行奇异值分解。将该段信号划分成10段时间序列，每段10240个采样点，对每段时间序列进行奇异值分解，取前6阶奇异值。根据分解后的奇异值进行信号重构，然后拼接成具有等采样点的信号。对其进行傅里叶变换和包络解调，其频谱图和包络谱图分别如图6、图7所示。

图6　奇异值处理后信号的频谱

图7　奇异值处理后信号的包络谱

由图6可知，利用滑移时间序列奇异值分解对高频细节信号D2进行特征提取以后，其频率成分与小波分解后相邻频段的频率混叠现象有了明显改善。由图7可知，经特征提取后信号的包络谱中优势频率依然为58.5Hz，二倍频能量相对较大，由此，可以判断出滚动轴承内圈存在故障。通过与图5进行比较，可发现图7所示包络谱中优势频率58.5Hz更为明显。

5结束语

小波-滑移时间序列奇异值分解法主要解决以下两个问题：①小波变换后相邻频带信号频率混叠问题；②因采样点数过多计算机无法进行奇异值分解或计算时间过长问题。该方法首先通过小波变换将原始采样信号分解到不同频段内，然后将其分解成若干子序列，对每个子序列进行奇异值分解，根据奇异值提取所需特征信息。最后，将每段子序列按采样先后顺序进行拼接，获得理想信号。利用该方法，对滚动轴承运行过程中的声音信号进行了处理，验证了方法的可行性。

[参考文献]

[1] 马伦,康建设,孟妍,等. 基于Morlet小波变换的滚动轴承早期故障特征提取研究[J]. 仪器仪表学报,2013,34(4):920-926.

[2] 张丹,侯力,曾颖峰,等. 基于小波消噪的主轴回转精度动态测量法[J].组合机床与自动化加工技术,2015(5):73-75,79.

[3] 郑思莉,桂预风,陈先桥,等. 小波阈值法在机械信号降噪研究中的应用[J]. 机械设计与制造,2014(1):222-225.

[4] 吕飞飞,崔凤奎,王晓强,等. 航空滚动轴承振动信号的小波降噪研究[J]. 机械研究与应用,2014(2):89-91.

[5] 周大志,钟功祥,吴英. 非线性小波阈值选取形式对小波降噪效果的影响分析[J]. 四川理工学院学报(自然科学版),2014,27(3):50-54.

[6] 蔡敏. 小波阈值法降噪分析与改进[J]. 信息与电子工程,2011,9(2):211-214.

[7] 赵学智,叶邦彦,林颖. 奇异值分解对轴承振动信号中调幅特征信息的提取[J]. 北京理工大学学报,2011,31(5):572-577.

[8] 李国宾,关德林,李廷举. 基于小波包变换和奇异值分解的柴油机振动信号特征提取研究[J]. 振动与冲击,2011(8):149-152.

[9] 赵学智,叶邦彦,陈统坚. 奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J]. 机械工程学报,2010,46(1):100-108.

[10] 汤宝平,蒋永华,张详春. 基于形态奇异值分解和经验模态分解的滚动轴承故障特征提取方法[J]. 机械工程学报,2010,46(5):37-42,48.

[11] 冯广斌,朱云博,孙华刚,等. 一种有效奇异值选择方法在微弱信号特征提取中的应用[J]. 机械科学与技术,2012,31(9):1449-1453.

[12] 赵学智,叶邦彦,陈统坚. 基于小波—奇异值分解差分谱的弱故障特征提取方法[J]. 机械工程学报,2012,48(7):37-48.

(编辑赵蓉)

Mechanical Fault Diagnosis Using Wavelet Analysis and SVD

LI Hong-liang,HUANG Min,GAO Hong,MA Chao

(School of Eleclromechanical Engineering, Beijing Information Science &Technology University, Beijing 1000192, China)

Abstract：To solve frequency mixing problem of the adjacent two frequency band signal after wavelet transform and unable to calculating or calculate time too long because of the excessive number of sampling points in singular value decomposition process, wavelet transform- sliding time series of singular value decomposition method was proposed. The original sample signal is decomposed into different frequency by wavelet transform, processing the required frequency band signal by sliding time series of singular value. Then, the signal is divided into a number of equal length sub time series by using the signal in the desired frequency band, extracting feature information according to the singular values. Operation the sound signal of inner ring fault of rolling bearing by this method and proved to be feasible.

Key words：wavelet transform; SVD; slip time series; feature extraction

文章编号：1001-2265(2016)06-0081-03

DOI:10.13462/j.cnki.mmtamt.2016.06.021

收稿日期：2015-07-12;修回日期：2015-08-08

*基金项目：国家科技重大专项资助项目(2013ZX04011012)

作者简介：李宏亮(1989—)，男，北京市人，北京信息科技大学硕士研究生，研究方向为机电系统故障诊断，(E-mail)shjshlhl@126.com。

中图分类号：TH17;TG506

文献标识码：A