基于拓扑优化的龙门加工中心横梁轻量化设计*

孙　芹，张进生，刘伟虔，刘　洋，于　慧，李作丽

(1. 山东英才学院，济南　250104；2.山东大学 a.机械工程学院;b.高效洁净机械制造教育部重点实验室，济南　250061)

基于拓扑优化的龙门加工中心横梁轻量化设计*

孙芹1,2a,2b，张进生1,2a,2b，刘伟虔2a,2b，刘洋2a,2b，于慧1，李作丽1,2a,2b

(1. 山东英才学院，济南250104；2.山东大学 a.机械工程学院;b.高效洁净机械制造教育部重点实验室，济南250061)

摘要：以大型铝材构件高速高效龙门加工中心的焊接横梁为研究对象，确定其结构原始方案，并对该方案进行静动态特性分析，获取主轴组件沿机床Y/Z向移动时刀头的位移情况以及横梁的前六阶固有频率和振型。基于变密度法对连续体结构横梁进行了拓扑优化设计,建立了最大刚度设计的拓扑优化模型和特征值问题的结构动力学拓扑优化模型。在Hypermesh/Optisruct中建立了不同优化模型的目标函数、约束条件、优化变量，对横梁的板筋布置、后壁板分别进行的优化。与优化前的结构相比较横梁的重量减轻11.5%，实现了横梁的轻量化设计，同时横梁的综合性能得到了明显的改善。

关键词：焊接横梁；Optistruct；静动态；拓扑优化；轻量化设计

0引言

机床轻量化技术是指在确保机床刚度和加工精度的前提下，减轻机床重量，降低机床使用时能量的消耗。横梁作为定梁动柱龙门式机床的主要移动部件，更是机床轻量化设计的重点。国内外横梁的轻量化研究主要集中在两个方面[1]：一是通过改变结构材料降低自重，如以焊接结构代替铸造结构、采用铝合金、新型复合材料等代替钢和铸铁；二是改变结构形式，寻求最合理的截面形状、筋板布置、减重孔形状。近年来兴起的结构优化设计是根据算法合理分配优化对象(比如尺寸等设计参数、形状、材料)以保证横梁整体的刚度、模态等特性，从而让横梁结构设计摆脱了对经验的盲目依赖[2-3]。拓扑优化是结构优化的一种，通过将单元离散，并赋予伪密度值，在设计空间内，寻求最佳材料分布，实现结构减重、动静态性能提高的目标[4-6]。

本文拟从结构上对横梁进行轻量化研究，并基于拓扑优化模型，调整横梁筋板布置，完成最大刚度的设计，同时需要降低横梁自重。通过对机床横梁结构进行拓扑优化设计，提出一种降低自重、提高综合性能的设计方法，对于推进结构优化在工程实际中的应用具有重要研究意义。

1加工中心整体布局及焊接横梁初始模型设计

1.1加工中心整体布局

大型铝材构件高速高效加工中心主要应用于轨道交通、船舶、航空航天用大型铝材构件加工领域，该加工中心采用床身、工作台固定，横梁、滑座、滑枕移动的定梁动柱龙门式结构，主要结构包括横梁、滑箱、滑柱、床身、工作台及两种刀库，总体布局如图1所示。

1.横梁 2.滑箱 3.立柱 4.滑柱 5.床身 6.圆盘式刀库 7.圆锯片立式刀库 8.工作台

图1大型铝构件高速高效加工中心总体结构布局图

1.2焊接横梁初始方案设计

初始横梁模型建立过程中，基于传统设计理念，考虑以下因素进行方案设计。

(1)壁厚。对于大型和超大型机床，壁厚一般不超过30mm。本文选取横梁截面尺寸为500×800mm，横梁壁厚取15mm。

(2)筋板布置。在考虑横梁承受空间载的情况下，内部筋板采用V型板与方板间隔布置，方板间隔为滑箱长度的1/2。

(3)焊接。钢板材料采用Q235，前壁板采用整体折弯件构成C型结构。焊接时V型板与方板顺序焊接，即方板绕C型板焊接，上下焊缝对称于中心避免出现收缩变形，V型开口处靠紧C型板，侧面靠紧方板进行焊接，采用断续焊增加焊缝阻尼能力，如图2所示。

图2　初始横梁结构CAD模型

2焊接横梁初始模型有限元分析

2.1静力学分析

对横梁的静态性能进行分析时主要获取滑座沿Y向左右移动和滑枕沿Z向上下移动时，刀头处的位移变化情况，分析示意图如图3所示。其中，研究滑枕沿Z向移时刀头变形时，考虑横梁受力最恶劣的工况，即滑箱位于横梁中部位置。主轴组件沿横梁左右移动、滑枕沿Z向上下移动时，刀头处位移分别如表1，表2所示。

图3　刀头位移变形检测示意图

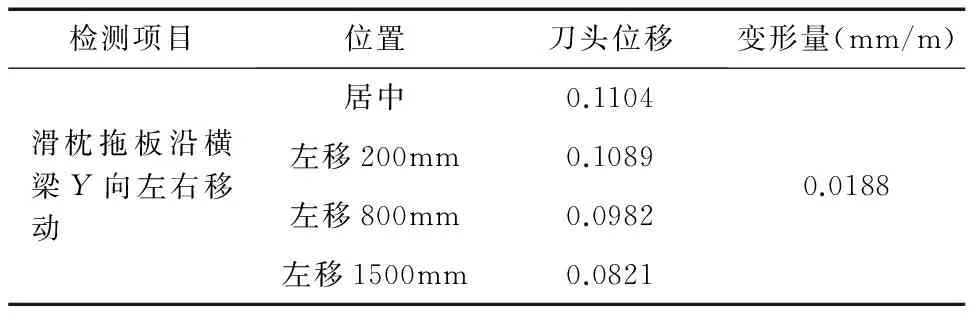
检测项目位置刀头位移变形量(mm/m)滑枕拖板沿横梁Y向左右移动居中0.1104左移200mm0.1089左移800mm0.0982左移1500mm0.08210.0188

表2　主轴组件沿Z向运动时刀头位移分析结果

一般情况下，龙门式加工中心参考标准全长0.04/1000，局部0.02/1000,Z向移动参考标准为0.03/500。从标准来看横梁结构抗弯度满足设计标准，静刚度良好。

2.2模态分析

横梁属于连续体，质量和弹性是连续分布的，理论上有无穷多阶模态，因结构的振动特性一般是有其低阶振动特性决定的[7]，故分析时只取其前6阶固有频率进行分析。对横梁三维模型进行简化并定义材料属性及结合面参数；采用8节点的Solid45单元结构，运用自由网格划分类型对横梁进行划分网格，获得横梁有限元模型，共生成314423个节点，67372个单元；对有限元模型施加边界条件并完成Frequency Finder设置后求解，获得横梁前6阶振型云图如图4所示。

前6阶模态分析固有频率分别为103Hz、164Hz、184Hz、238Hz、313Hz、387Hz，固有频率均在100Hz以上，且以整体振型为主。从上述云图还可以看出在前几阶振型尤其是一、二阶振型，最大振幅出现在横梁中间位置，说明在现有筋板布置情况下此位置振动较大。在5、6阶频段，横梁出现局部较大变形，集中在横梁的两端，此处在313Hz、387Hz频率共振频率下较为薄弱。

图4　横梁结构的前6阶固有频率及振型

3横梁结构的拓扑优化

从上述对横梁的静动态特性分析来看，横梁结构的整体刚性较好，固有频率均高于100Hz。拓扑优化主要进行以下工作：在删除冗余材料的同时，针对局部薄弱环节进行内部筋板的调整，并实现固有频率及刚度的最大化。前期的模型准备包括网格离散化、连接单元定义、网格质量检查、属性定义、工况设置、定义约束条件、目标函数以及载荷步设置等[8]。

3.1横梁内部筋板布局优化

在原有结构基础上对横梁内部筋板布置进行优化。以单阶固有频率最高为优化目标，以体积分数volfrac(优化后的体积/原有体积)作为约束函数，volfrac=0.8。选取Optistuct为Hypermesh求解器设定为Optistuct；空间中每个单元的密度(和相应单元的刚度)为变量，求解前六阶固有频率。

本次分析，选取MINDIM=30，ISCRETE=2.0。以第1阶、第2阶固有频率最高为目标函数，拓扑优化后的密度分布云图如图5所示。

(a)一阶固有频率优化伪密度云图

(b)二阶固有频率优化伪密度云图

对图5优化伪密度云图进行分析，其中红色区域部位需要添加加强筋，蓝色区域材料可以去除。根据图5a，左右两侧红色区域需要两块斜筋板加强前端壁板，而顶部壁板不需要加强筋。据图5b，前壁板和顶部壁板红色区域均需要加强，因此加强筋应同时连接前壁板和顶部，由于待加强区域纵向较宽，应密集布置间隔板。筋板布置简图如图6所示。

图6　横梁板筋布置简图

3.2筋板及后壁板拓扑优化

横梁内部筋板布局优化后，需对筋板及后壁板进行减重设计。在进行横梁的拓扑优化时，一方面要实现固有频率最大化，另一方面还要保证刚性足够、质量降低等要求，实际上属于多目标优化的范畴。在拓扑优化理论中实现多目标优化常采用的线性加权法，将多目标问题转化为单一目标，但对于非凸优化问题而言，不能确保得到所有的Pareto最优解[9]，且加权系数的选取具有较强的主观性。

(a)中间筋板密度分布云图

(b)侧筋板密度分布云图

(c)后壁板密度分布云图

以柔度值最小(compliance=min)为优化目标，一阶固有频率freq1≥112，二阶固有频率freq2≥150，volfrac=0.8，变量同前。

随着惩罚因子DISCRETE的增大，结构的柔度逐渐降低，即结构的刚性增大[10]。取DISRETE=2，MINDIM=30，控制精度OBJTOL=0.001。分别设置内部筋板单元、后壁板单元为设计变量得到密度分布云图如图7所示。

从图7a和7b可以看出，拓扑结构较好，过渡的密度单元少，边界清晰。而图7c中，后壁板密度分布云图出现部分过渡密度单元，说明设置的参数不合适，可通过调节惩罚因子、最小成员尺寸等参数使密度单元向0，1离散。对优化后的横梁结构进行可制造化处理，最终得到的三维结构如图8所示。

(a)优化后的筋板实体模型

(b)优化后的后壁板实体模型

4优化结果对比分析

对优化后的横梁结构进行静力学分析和模态分析，并将分析结果与初始方案分析结果进行对比将优化后的横梁模型导入Ansys Workbench中进行网格划分，分析内容同本文第2部分，包括横梁在自重作用下刀头位移及前六阶模态分析。优化前后的数据对比如表3、表4及表5所示。

表3　主轴组件沿横梁Y向移动刀头位移比对

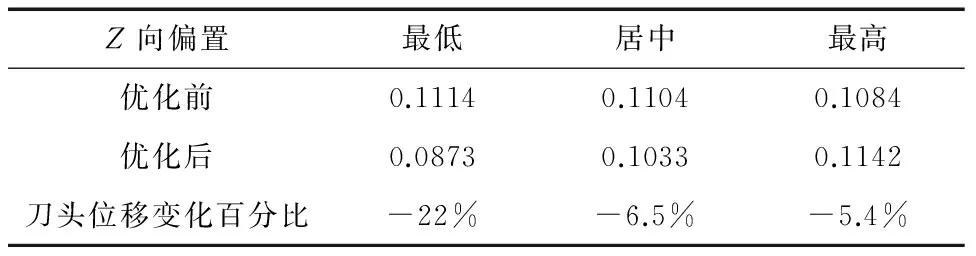
表4　滑枕Z向移动刀头位移比对

表5　优化后的模态频率比对

从表3和表4可以看出，优化后刀头变形均有所降低。表4中，在滑枕处于最高位置时，刀头变形优化后为0.1142，优化前为0.1084，变形量有所增加，原因可能为优化时仅考虑特定工况且施加载荷为静态力，可能导致某一位置的变形比预期要大一些。

图9为横梁优化后振型云图，从表5及图9可以看出，优化后横梁中部动态性能得到了明显改善，且振动幅值降低。从表5可以看出，优化后，固有频率尤其是一阶固有频率得到了明显提升。第6阶固有频率由387变为335，相对于初始值有所降低，即所谓的目标(约束)函数振荡问题。6阶频率属较高频率段，因此优化结果仍然符合目标。

图9　模态分析云图

借助于Solidworks软件查看重力属性，质量m优化前后分别为2204kg和1950kg，优化后减重11.5%。

5结论

(1)对焊接横梁的初始模型进行了静力学分析。讨论了在自重作用下，滑座沿Y向左右移动和滑枕沿Z向上下移动时，刀头的变形情况；模态分析过程中，获取了前6阶固有频率。静力学分析结果作为拓扑优化的依据

(2)在调整内部筋板时，基于动力优化以提高固有频率为目标，获取了影响低阶固有频率的区域，并通过筋板对横梁进行了加强；在结构减重时，以最小柔度为目标、同时约束了体积分数和前几阶固有频率的下限值，实现了最大刚度的拓扑优化设计。

(3)对横梁进行了轻量化设计。基于拓扑优化模型，调整横梁筋板布置，完成最大刚度的设计，同时降低了横梁自重。优化后，横梁重量减轻11.5%，综合性能得到了明显的改善。

[参考文献]

[1] 董惠敏,丁尚,王海云,等. 床鞍的轻量化设计数据库研究[J]. 组合机床与自动化加工技术,2014(3):33-36.

[2] 钟群鹏,有移亮,张峥,等.机械装备构件轻量化主要技术途径的探讨[J].机械工程学报. 2012, 48(18):2-6.

[3] 孙守林,刘建栋,董惠敏,等. 机床主轴箱轻量化设计流程研究[J]. 组合机床与自动化加工技术,2014(12):14-18.

[4] Stolpe M, Svanberg K.An alternative interpolation scheme for minimum compliance topology optimization[J].Structural and Multidisciplinary Optimization.2001,22(2):116-124.

[5] Rozvany G I N. Aims, scope, methods, history and unified terminology of computer-aided topology optimization in structural mechanics[J]. Structural and Multidisciplinary Optimization, 2001, 21(2):90-108.

[6] Bendsøe M P, Sigmund O. Material interpolation schemes in topology optimization[J].Archive of Applied Mechanics,1999,69(9-10):635-654.

[7] 季彬彬, 张森, 杨玉萍, 等. GMF3022 龙门加工中心横梁的模态及谐响应分析[J]. 组合机床与自动化加工技术, 2013 (10): 36-38.

[8] 李珊珊,丛明,王贵飞,等. 基于变密度法的床鞍结构拓扑优化设计[J]. 组合机床与自动化加工技术,2014(4):19-21,25.

[9] 杨彩芳, 殷国富, 苏龙. 龙门加工中心立柱性能分析与拓扑优化设计[J]. 组合机床与自动化加工技术, 2013 (2): 50-53.

[10] 刘甚宏, 关英俊, 张力锋, 等. XK2423 数控铣床立柱的有限元分析与拓扑优化[J]. 组合机床与自动化加工技术, 2014(8): 22-25.

(编辑赵蓉)

Lightweight Design of the Gantry Machining Center Beam Based on Topology Optimization

SUN Qin1,2a,2b, ZHANG Jin-sheng1,2a,2b,LIU Wei-qian2a,2b, LIU Yang2a,2b, YU Hui1, LI Zuo-li2a,2b

(1. ShanDong Ying Cai College, Jinan 250104, China;2 a.School of Mechanical Engineering;b.Key Laboratory of High-Efficiency and Clean Mechanical Manufacture,Ministry of Education,Shandong University, Jinan 250061, China)

Abstract：Static and dynamic characteristics of the welded beam original program for large aluminum components high speed and high efficient gantry machining center were analyzed in the paper. The displacement of the tip,the first six natural frequencies and mode shapes of the beam were obtained when spindle assembly moving along the Y/Z direction. Topology optimization design of the continuous beam structure was conducted based on the variable density method, and the topology optimization model of maximum stiffness design and eigenvalue problem structural dynamics was established at last. The objective function, constraints and optimization variables of the different optimization model were established in Hypermesh/Optistruct, and the rib arrangement and weight of the beam were optimized respectively. Compared with the structure before optimization, the weight of the beam was reduced about 11.5%, so it can be said that the lightweight design of the welded beam was achieved and the comprehensive performance of the beam was significantly improved.

Key words：the welded beam; Optistruct; static and dynamic; topology optimization; lightweight design

文章编号：1001-2265(2016)06-0008-04

DOI:10.13462/j.cnki.mmtamt.2016.06.003

收稿日期：2015-07-29；修回日期：2015-08-28

*基金项目：山东省高等学校科技计划项目(J13LB63)；山东省重点研发计划(2015GGB01179)

作者简介：孙芹(1979—)，女，山东乳山人，山东英才学院副教授，研究方向为机械产品设计和制造自动化，(E-mail)sunqin1998@163.com； 通讯作者：张进生(1962—)，男，山东高青人，山东大学教授，博士研究生导师，研究方向为脆硬材料(石材)高效加工技术研究及装备研发，(E-mail)zhangjs@sdu.edu.cn。

中图分类号：TH16; TG502

文献标识码：A