在小学数学教学中发展学生合情推理能力

李玉月

【关键词】小学数学 课堂教学 推理能力

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2016）06A-0037-02

推理一般包括合情推理和演绎推理，合情推理是从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果。合情推理的应用非常广泛：在日常生活中，人们经常运用“由此可见……”“想必……”“如果……那么……”等句式阐述自己的看法，这是人们在运用合情推理进行思维的表现。在数学学习上，合情推理是探索解决问题的思路和发现数学结论的重要手段。那么，如何在数学教学中有效地发展学生的合情推理能力，培养学生的理性思维和创新能力呢？

一、在解决问题中渗透大胆猜想的意识

猜想是合情推理不可缺少的因素，也是数学学习活动中最活泼的因素之一。在学习过程中，学生一旦形成自己的猜想，就会自发地投身于各种探究活动中，积极地对猜想进行相对合理的证实或判断，主动去经历知识形成的全过程，从而获得真正的体验。

在数学学习中的猜想不是凭空想象，更不能随意杜撰，必须是根据事实情境理性思考后进行的猜测或假设。因此，教师在解决问题过程中鼓励学生猜想时，必须先引导学生认真阅读、观察问题情境，在事实的基础上进行有序思维，提出猜想。如人教版数学一年级上册第79页例6的解决问题：

例题以图文结合的形式出示了两条信息，提出了这样一个问题：小丽和小宇之间有几人？在教学中，教师除了要重视教给学生解决问题的基本方法，还要抓住契机培养学生的猜想意识。教师可以这样安排教学环节：让学生认真阅读主题图，用自己的话说说“排第10”和“排第15”的意思，在学生深入理解“小丽排第10”和“小宇排第15”的意思后，提出小组活动要求：猜一猜小丽和小宇之间有几人？在小组内说一说，你是怎么想的。活动要求一提出来，学生的思维顿时被激活了，他们非常热烈地讨论起来。性急的学生随意说了一个比较大的数字，同组的同学马上反驳：“不可能！小宇排第15，不可能比15大！”该生的话引发大家根据从图中获取的信息去猜想到底小丽和小宇之间有几人，并根据自己已有的认知经验说出猜想的理由。随着讨论的深入，学生们猜想的结果越来越接近，甚至就是正确的答案。最后，在教师的引导下，学生们用数数、画图等策略验证了自己的猜想。在本案例教学中，学生们经过猜想、争论、验证等过程，不但深化了对数的大小、基数、序数的有关知识，更丰富了他们解决问题的经验，培养了他们大胆猜想的意识，合情推理能力得以提高和发展。

二、在图形与几何教学中培养小心求证的能力

在教学中渗透猜想的意识，只是发展学生合情推理能力的一小步。“大胆猜想，小心求证。”（胡适语）是科学研究的基本要求。对于正确的数学结论的形成，光凭直觉或经验进行猜想、判断是不够的，还必须有小心求证的过程。唯有如此，才是一个完整的、科学严谨的学习探究过程。

如，人教版数学五年级上册《多边形的面积》第一课时《平行四边形的面积》的教学，在学习此课之前，学生已掌握了平行四边形的特征并能够灵活运用长方形、正方形的面积计算公式解决相关问题。上课伊始，笔者先安排一个数格子活动，引导学生对比大小相同的长方形与平行四边形的底与长、高与宽、面积之间的关系。学生们在观察、联想、猜测后得出两个不同的结论：平行四边形的面积=底×高，或平行四边形的面积=底边×斜边。到底哪个结论正确呢？大部分学生不相信平行四边形的面积=底边×斜边是正确的，但为什么不正确却很难用语言说明清楚。此时正是引导学生通过动手实验，进行小心求证的最佳时机。第一步：根据观察的结果猜想，能不能把平行四边形转化成熟悉的图形来计算它的面积。第二步：想办法实现两个图形的转化。第三步，认真观察原来的平行四边形和转化后的图形，你有什么发现？学生在以前的数学学习中已经接触过转化的思想，积累了一定的活动经验，因此他们很快想出办法，利用不同的割补方法将平行四边形转化成长方形。再通过观察，发现了转化前后图形之间的等量关系，推导出正确的平行四边形面积公式。“观察猜想—割补转化—推导结论”是本课学习的重难点，因此，要留给学生充足的时间让他们反复边操作边叙述推导的过程。在本活动环节结束后，“平行四边形的面积=底边×斜边”是不正确的就不言而喻了。在这个推导平行四边形面积公式的活动中，遵循了“大胆猜想、小心求证”的科学探索原则，使学生在猜想和求证中，完成了新知的建构，进一步发展了合情推理的能力。

三、在概念教学中学习归纳、类比的方法

数学概念是数学知识体系的重要组成部分，也是小学数学教学的重要内容。而数学概念较为抽象，学生不易理解和掌握。因此，教师在教学时必须想方设法组织趣味性强的学习活动，为学生创造积极参与、交往互动、共同发展的学习平台，让学生亲身经历概念的形成过程。

如人教版数学五年级下册有关“因数和倍数”的知识，属于初等数论基础知识的范畴。这部分内容对学生来说，既具有很强的魅力，也因其具有的抽象性而存在很大的挑战。以本册第8页的思考题为例：

14、21都是7的倍数，14和21的和是7的倍数吗？18、27都是9的倍数，18和27的和是9的倍数吗？

这道思考题的结论是：如果任意两个数是一个数的倍数，那么，这两个数的和也是这个数的倍数。若直接把这一结论呈现给学生，再让学生通过练习来巩固记忆，学生可以清楚地复述结论，并运用结论对一些数的特点进行判断。但很显然，这样的学习，学生只能依葫芦画瓢，知其然而不知其所以然。如何让学生发现、理解并掌握这个规律呢？教师可以这样设计小组活动：①判一判，14和21的和、18和27的和分别是7、9的倍数吗？②想一想，你还能举出类似的例子吗？③分别观察每组式子，你发现了什么？④你能用自己喜欢的方式来描述你的发现吗？学生按活动要求，根据已有的四则运算的知识和经验，很快可以列出以下等式：

14=2×7，21=3×7

14+21=2×7+3×7=（2+3）×7

66=6×11，99=9×11

66+99=6×11+9×11=（6+9）×11

……

18=2×9，27=3×9

18+27=2×9+3×9=（2+3）×9

48=6×8，72=9×8

48+72=6×8+9×8=（6+9）×8

……

写着写着，有学生率先说：“老师，要写多少个？写不完的！永远也写不完！”他的话引起大家的共鸣。此时教师问：为什么呢？每组等式之间有什么共同点？能不能用一组式子把这些无数的式子表示出来？于是，抽象思维能力强的学生用字母表示数，列式如下：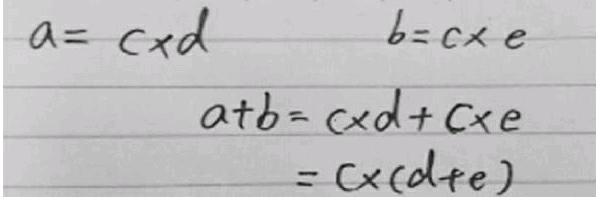

也有学生用图形表示数，列出如下式子：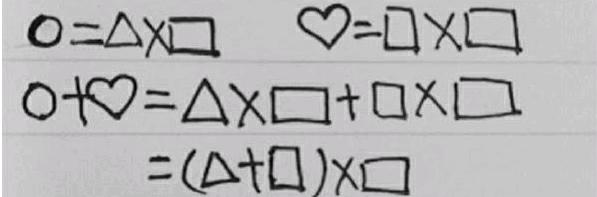

还有学生直接描述为：

教师在肯定学生的想法，要求学生根据式子组织好语言叙述结论后，又提出一个问题：如果3个数、4个数或者更多都是同一个数的倍数，这些数的和是不是这个数的倍数呢？这次，学生们没有花太多时间，就讨论出肯定的结果，将结论推广为：如果有n个数都是一个数的倍数，那么这n个数的和也是这个数的倍数。这样，学生通过观察实例、枚举类比，发现了例举的等式的共性，自觉运用了不完全归纳法归纳总结出结论，经历了由特殊到一般的推理过程，合情推理能力在润物无声中得到了发展。

总之，促进学生合情推理能力的发展和提高需要一个长期、循序渐进的过程。在教学中，教师不但要使学生理解和掌握基本的数学知识与技能，还要有意识地捕捉教学契机，培养学生思考的条理性，促进学生合情推理能力的形成，养成良好的数学素养，使数学学习成为促进学生全面发展的重要组成部分。

（责编 林 剑）