一类扭形变Schrödinger-Virasoro李代数的自同构群

徐　坤，高寿兰

（1.同济大学数学系，上海200092；2.湖州师范学院理学院，浙江湖州313000）

一类扭形变Schrödinger-Virasoro李代数的自同构群

徐坤1，高寿兰2

（1.同济大学数学系，上海200092；2.湖州师范学院理学院，浙江湖州313000）

摘要：对一类带有两个参数的扭形变Schrödinger-Virasoro李代数Lλ,μ进行了研究.计算了当的一维中心扩张的自同构，并讨论了某些特殊的自同构生成的子群之间的关系，最后确定了�λ,μ的自同构群Autλ,μ）的结构.

关键词：Virasoro李代数；扭形变Schrödinger-Virasoro李代数；自同构

1　引言

无限维李代数的结构理论与表示理论在数学物理上具有非常重要的作用.在统计物理的背景下文献［1-2］分别引入了Schrödinger-Virasoro李代数及其形变.随后出现了一系列与之相关的研究工作.例如，文献［3］确定了Schrödinger-Virasoro李代数的自同构群；文献［4］给出了扩张情形下的Schrödinger-Virasoro李代数的导子代数，中心扩张和自同构群；文献［5］讨论了扭形变Schrödinger-Virasoro李代数的导子代数和自同构群.

特别地，文献［6］讨论了扭形变Schrödinger-Virasoro李代数Lλ,μ的二上同调群. Lλ,μ是复数域C上的线性空间，有一组基，对任意的m,n∈Z,满足下列李运算：

其余为零.文献［6］得到了下列结论：

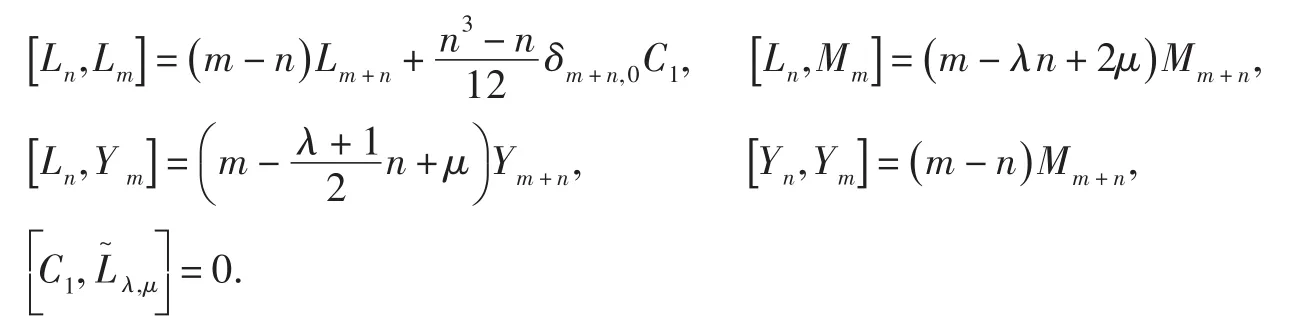
本文中，用Z，C和C∗分别表示整数集、复数集和非零复数集，所有的向量空间都是在复数域C上.

2　λ,μ的自同构

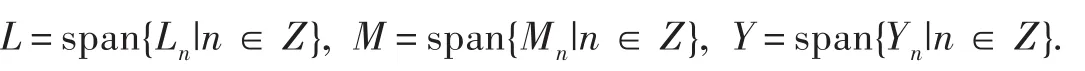
参考文献：

［1］HENKEL M. Schrödinger invariance and strongly anisotropic critical systems［J］. J Stat phys, 1994, 75：1023-1029.

［2］ROGER C, UNTERBERGER J. The Schrödinger-Virasoro Lie Group and Algebra：Representation Theory and Cohomological Study ［J］. Annales Henri Poincaré, 2006, 7（7-8）：1477-1529.

［3］GAO S L. The Automorphism Group of the Schrödinger-Virasoro Lie Algebra［J］. Journal of Huzhou Teachers College, 2010, 32 （1）：6-10.

［4］GAO S L, JIANG C P, PEI Y F. Structure of the Extended Schrödinger-Virasoro Lie Algebra［J］. Algebra Colloq, 2009, 16（4）：549-566.

［5］WANG W, LI J, XU Y. Derivations and automorphisms of twisted deformative Schrödinger-Virasoro Lie algebras［J］. Communication in algebra, 2012, 40：3365-3388.

［6］LI J B. 2-Cocyles of Twisted Deformative Schrödinger-Virasoro Algebras［J］. Communications in Algebra, 2012, 40（6）：1933-1950.

［7］GAO S. The structure and representations of Schrödinger-Virasoro algebra and non-graded Virasoro-like Lie algebras［D］. Shanghai：Shanghai Jiaotong University, 2008.

The Automorphism Group of a Class of Twisted Deformative Schrödinger-Virasoro Lie Algebra

XU Kun1, GAO Shoulan2
（1. Department of Mathematics, Tongji University, Shanghai 200092, China；2. School of Science, Huzhou University, Huzhou 313000, China）

Abstract：In this paper，the authors mainly study the twisted deformative Schrodinger-Virasoro Lie algebra Lλ,μwith two parameters. The automorphisms of one dimensional center extension offor λ∈C,μis calculated and the relationships between certain subgroups generated by several special automorphisms are discussed. Finally, the structure of the automorphism groupis characterized.

Key words：Virasoro algebra；twisted deformative Schrödinger-Virasoro algebra；automorphism

中图分类号：O152.5

文献标识码：A

文章编号：1008-2794（2016）02-0079-07

收稿日期：2015-09-20

基金项目：国家自然科学基金“共型流李代数的结构与表示”（11201141）；国家自然科学基金“几类无限维李代数与超共形代数的研究”（11371134）；浙江省自然科学基金“无限维李代数与顶点算子（超）代数的结构与表示”（LQ12A01005）；浙江省自然科学基金“无限维李代数、李伪代数与共形代数的研究”（LZ14A010001）

通信作者：徐坤，硕士研究生，研究方向：李代数，E-mail：1531948@tongji.edu.cn.