Heisenberg Jordan-Lie代数的自同构群

周 佳

(吉林农业大学 信息技术学院,长春 130118)

HeisenbergJordan-Lie代数的自同构群

周 佳

(吉林农业大学 信息技术学院,长春 130118)

通过给出Heisenberg Jordan-Lie代数的定义,得到Heisenberg Jordan-Lie代数H的自同构群Aut(H)的一些子群,并在H为低维的情形下,讨论了自同构群Aut(H)的基本结构.

Heisenberg Jordan-Lie代数; 自同构群; 子群

0 引 言

基于对Lie代数和Lie超代数的研究[1-5],Okubo等[6]提出了Jordan Lie超代数的概念,其与Lie代数密切相关.目前,关于Heisenberg Lie代数的研究已有许多成果[7-8].本文在Heisenberg Lie代数自同构群[9]的基础上,得到了Heisenberg Jordan-Lie代数的自同构群及其相关性质.

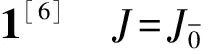
1) [a,b]∈Jα+β;

2) [a,b]=-δ(-1)αβ[b,a](阶化反对称);

3) [a,[b,c]]=[[a,b],c]+(-1)αβ[b,[a,c]](阶化Jacobi等式).

定义3令

做运算：

易知H关于该运算构成一个δ-Jordan超代数,称为δ-Jordan Heisenberg代数.当δ=1时,H称为Heisenberg超代数.当δ=-1时,H称为Heisenberg Jordan-Lie代数.

本文仅讨论δ=-1情形下的Heisenberg Jordan-Lie代数H.

1 主要结果

1.1H自同构群Aut(H)的一些子群

1.1.1 内自同构群

定理1对h0∈H,d=diag(d1,d2,…,dn+2)可逆,取a=d+h0,定义φa(h)=aha-1,∀h∈H,则φa是H的一个自同构.

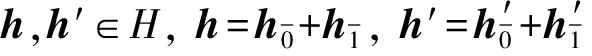
而

从而φa[h,h′]=[φa(h),φa(h′)].则φa是H的一个自同构.

定理2令G1为H所有内自同构构成的集合,则G1是Aut(H)的子群.

证明: 对∀φa,φb∈G1,h∈H有φaφb(h)=φab(h).令a=d1+h1,b=d2+h2,则

ab=d1d2+(d1h2+h1d2+h1h2)=d3+h3,

从而φab∈G1.

定义5称G1为H的内自同构群.

1.1.2 中心自同构群

在竞争日趋激烈并且增速逐渐放缓的SUV市场，想要获得消费者的青睐必须要有独到之处。东风雷诺新科雷嘉在智能互联和安全性上的优势还是值得称赞的，考虑到它13.98万元至19.48万元的售价，对于它在市场上的表现还是值得一番期待的。

定理3对α=(a1,b1,a2,b2,…,an,bn)∈C2n,定义φα:H→H,使得

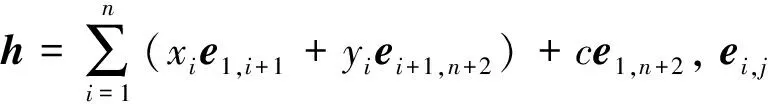
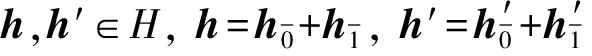
而

从而φα[h,h′]=[φα(h),φa(h′)].则φα是H的一个自同构.

定义6称φa是H的中心自同构.

定理4令G2为H所有中心自同构构成的集合,则G2是Aut(H)的子群.

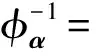
定义7称G2为H的中心自同构群.

1.1.3 对合自同构群

定理5令r=(e1,n+2+e2,n+1+…+en+2,1),定义ω0:H→H,使得ω0(h)=-rhTr,∀h∈H,则ω0是H的一个自同构.

所以ω0是映射.由r=rT,且r2=e(单位矩阵),易知ω0是双射.

而

从而ω0[h,h′]=[ω0(h),ω0(h′)].则ω0是H的一个自同构.

定义8称ω0是H的对合自同构.

定理6令G3={1,ω0},这里1为恒等变换,则G3是Aut(H)的子群.

定义9称G3为H的对合自同构群.

1.1.4 第一类外自同构群

定理7令S是由{2,3,…,n+1}n个文字的置换生成的对称群,

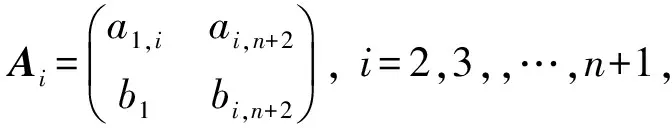
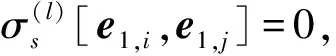
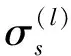
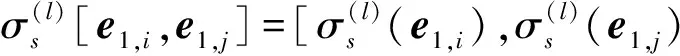
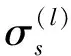
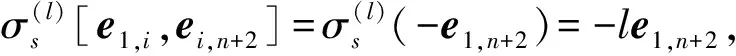
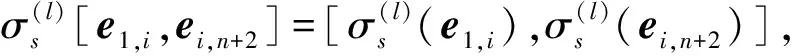
1.1.5 第二类外自同构群

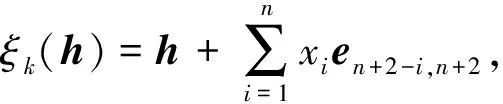
则ξk是H的一个自同构.

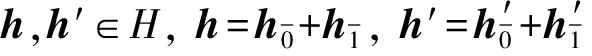
从而ξk[h,h′]=[ξk(h),ξk(h′)],则ξk是H的一个自同构.

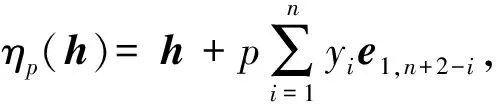
则ηp是H的一个自同构.

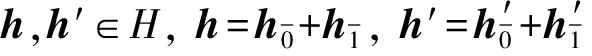
从而ηp[h,h′]=[ηp(h),ηp(h′)],则ηp是H的一个自同构.

定理10对q∈C,定义φq:H→H,使得

φq(h)=h+qxie1,n+1-qyne2,n+2,

则φq是H的一个自同构.

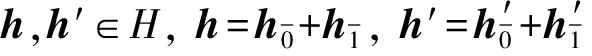
从而φq[h,h′]=[φq(h),φq(h′)],则φq是H的一个自同构.

定理11对r∈C,定义ψr:H→H,使得

ψr(h)=h+rxne1,2-ry1en+1,n+2,

则ψr是H的一个自同构.

证明同前.

定义11ξk,ηp,φq,ψr统称为H的第二外自同构,由所有ξk,ηp,φq,ψr生成的Aut(H)的子群G5称为H的第二类外自同构群.

注2易验证： {ξk|k|∈C},{ηp|p|∈C},{φq|q|∈C},{ψr|r|∈C}全是Aut(H)的子群.

1.2低阶Heisenberg-Jordan-Lie代数自同构群的确定

1.2.1n=0时H的自同构群

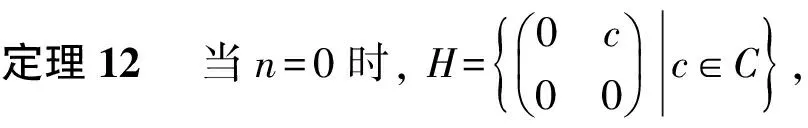
1.2.2n=1时H的自同构群

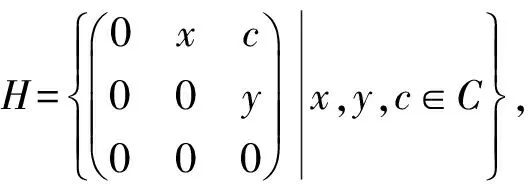
证明: 对∀φ∈Aut(H),令

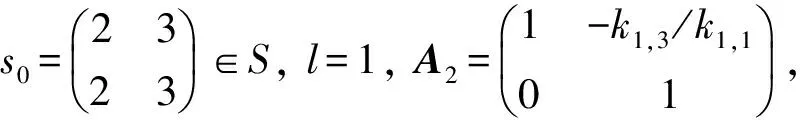
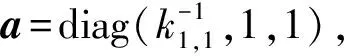
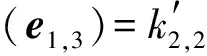
从而φ是有限个内自同构、 中心自同构、 对合自同构和第一类外自同构的乘积.

1.2.3n=2时H的自同构群

引理1设φ是H的一个自同构,且

则

定理14当n=2时,Aut(H)中的每个元素都是有限个内自同构、 中心自同构、 对合自同构、 第一类外自同构和第二类外自同构的乘积.

证明: 因为φ∈Aut(H),且H的中心C(H)={ke1,4|k∈C}|,所以φ(e1,4)=ke1,4,k≠0.令

不妨设a1,a2中至少有一个非零,事实上,若a1=a2=0,则a3,a4至少有一个非零.若a3≠0,则用ωφ代替φ即可保证a2≠0.若a1≠0,则用ωφ代替φ即可保证a1≠0.进而不妨设a1≠0.事实上,若a1=0,则a2≠0,取0≠r∈C,得第二类外自同构ψr,用ψφ代替φ可保证a1≠0.

于是,取a=diag(1,a1,1,1),可得内自同构φα,用φαφ代替φ,则有φe1,2=a1e1,2.令

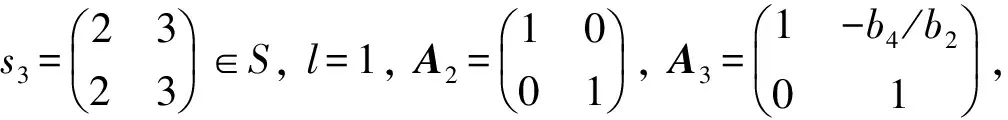
由引理1易得

从而d3=0,c3=k,c4=0,d4=k.所以有

其中k≠0.取α=(0,-c0/k,0,-d0/k)∈C4,得到中心自同构φα,用φαφ代替φ,则有

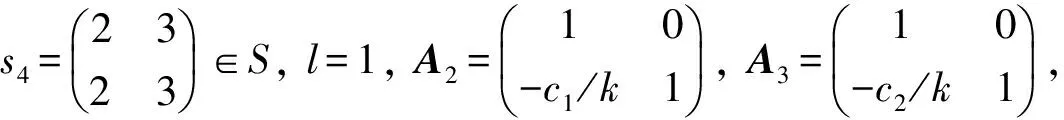
其中k≠0.

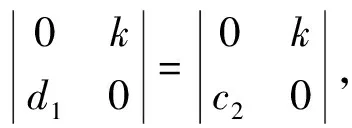
其中k≠0.取a=diag(1,1,1,k),得到内自同构φα,用φαφ代替φ,有

从而φ是有限个内自同构、 中心自同构、 对合自同构、 第一类外自同构和第二类外自同构的乘积.

[1]Jacobson N.Lie Algebras [M].New York: Wiley,1962: 23-24.

[2]Kac V G.Lie Superalgebras [J].Advances in Mathematics,1977,26(1): 8-96.

[3]孟道骥,朱林生,姜翠波.完备李代数 [M].北京: 科学出版社,2001: 23-25.(MENG Daoji,ZHU Linsheng,JIANG Cuibo.Complete Lie Algebras [M].Beijing: Science Press,2001: 23-25.)

[4]苏美,马瑶,陈良云.第一类李拟代数的基本性质 [J].东北师大学报: 自然科学版,2011,43(1): 1-5.(SU Mei,MA Yao,CHEN Liangyun.Elementary Properties of Lie-Like Algebra1-st[J].Journal of Northeast Normal University: Natural Science Edition,2011,43(1): 1-5.)

[5]Scheunert M.The Theory of Lie Superalgebra [M].Berlin: Springer-Verlag,1979: 270.

[6]Okubo S,Kamiya N.Jordan-Lie Super Algebra and Jordan-Lie Triple System [J].Journal of Algebra,1997,198(2): 388-411.

[7]孟道骥,朱林生.完备Lie代数的若干进展 [J].数学进展,1998,27(3): 193-201.(MENG Daoji,ZHU Linsheng.Some Advances on Complete Lie Algebras [J].Advances in Mathematics,1998,27(3): 193-201.)

[8]白瑞蒲,张蒙,刘丽丽.一类特殊的Heisenberg 3-李代数的结构 [J].应用数学,2011,24(2): 372-376.(BAI Ruipu,ZHANG Meng,LIU Lili.Structures of a Class of Heisenberg 3-Lie Algebra [J].Mathematica Applicata,2011,24(2): 372-376.)

[9]张海山,邵文武,卢才辉.Heisenberg李代数的自同构群 [J].首都师范大学学报: 自然科学版,2007,28(1): 1-7.(ZHANG Haishan,SHAO Wenwu,LU Caihui.The Automorphism Group of Heisenberg Lie Algebra [J].Journal of Captial Normal University: Natural Science Edition,2007,28(1): 1-7.)

(责任编辑： 赵立芹)

AutomorphismGroupofHeisenbergJordan-LieAlgebra

ZHOU Jia
(SchoolofInformationTechnology,JilinAgriculturalUniversity,Changchun130118,China)

We introduced the notion of Heisenberg Jordan-Lie algebra so as to investigate some subgroups of the automorphism group Aut(H) of Heisenberg Jordan-Lie algebraH.Moreover,we discussed some basic structure of the automorphism group Aut(H) in the case ofHbeing low-dimensional.

Heisenberg Jordan-Lie algebra; automorphism group; subgroup

2013-12-17.

周 佳(1982—),女,汉族,硕士,讲师,从事Lie代数的研究,E-mail: 1316023705@qq.com.

吉林省自然科学基金(批准号: 201215184)和吉林农业大学青年科研基金(批准号: 201329).

O152.5

A

1671-5489(2014)05-0873-08