极大加代数的对称代数S上互补基本矩阵
2016-06-30袁跃爽张子龙
袁跃爽,张子龙,2
(1.河北师范大学数学与信息科学学院,河北石家庄050024;2.河北省计算数学与应用重点实验室,河北石家庄050024)
极大加代数的对称代数S上互补基本矩阵
袁跃爽1,张子龙1,2
(1.河北师范大学数学与信息科学学院,河北石家庄050024;
2.河北省计算数学与应用重点实验室,河北石家庄050024)
主要研究了极大加代数的对称代数S上互补基本矩阵,给出本征积的概念,证明了S上的Laplace定理,由此推出所有互补基本矩阵的行列式相等,且任意两个互补基本矩阵的行列式中的非零项均一一对应相等.在一个互补基本矩阵的行列式中,对于确定非零项的任一置换,给出了在另一个互补基本矩阵的行列式中找到置换使其确定相同非零项的方法.
极大加代数;对称代数;互补基本矩阵;Laplace定理;行列式
§1 引 言
2014年,Fiedler和Hall给出了极大加代数上的互补基本矩阵[1]的概念,发现这些互补基本矩阵与传统代数中的互补基本矩阵[2]有些相似的代数性质,例如,互补基本矩阵的(极大)不变量等于各个矩阵(极大)不变量的乘积.极大加代数的对称代数S是一种重要的代数结构[3].文献[3]中引入了S上矩阵的行列式与行列式按照一行展开的概念. 2008年,Fiedler提出了多个矩阵的本征积[4]的概念,并得到互补基本矩阵是完全本征的.
本文引入S上互补基本矩阵,给出S上互补基本矩阵的完全本征性的证明,并提出S上k级子式的概念,证明了在S上的Laplace定理.
设A是n×n矩阵,A的行列式det(A)中共有n!项,则每项是由某个置换确定的矩阵中n个位置的元素作⊗积得到.根据Laplace定理,得到所有互补基本矩阵(相同的矩阵因子作积)的行列式相等,而且其中任意两个互补基本矩阵的行列式中的非零项均一一对应相等.
如果存在两个行列式中的项是一一对应的,那么也必定存在一一对应的置换.在一个互补基本矩阵的行列式中,对于确定非零项的任意置换,本文给出了定位法,根据定位法可以在另一个互补基本矩阵(相同的矩阵因子作积)的行列式中找到置换使其确定相同非零项.为了具体说明定位法,给出一个例子.
§2 预备知识
Rmax= R∪{-∞}为具有二元运算⊕和⊗的幂等交换半域,其中二元运算⊕和⊗分别是“取极大”和“加法”运算. Rmax的零元是ε= -∞,单位元是e = 0.是{(x,y)|x,y∈Rmax}上具有运算⊕和⊗的幂等半域,其中二元运算⊕和⊗定义如下:的零元是(ε,ε),单位元是(e,ε).
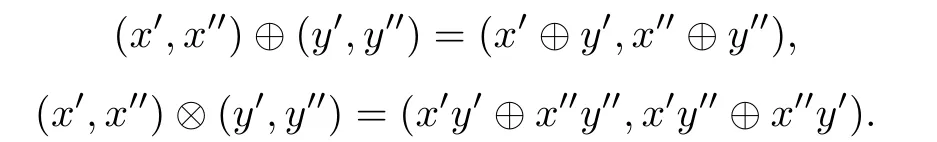
设x =(x′,x′′),规定⊖x =(x′′,x′)为x的负元,x•= x⊖x为x的平衡算子.
设x =(x′,x′′),y =(y′,y′′),如果x′⊕y′′= x′′⊕y′,那么称x与y平衡,记为x▽y.
在R2max上引入关系R:
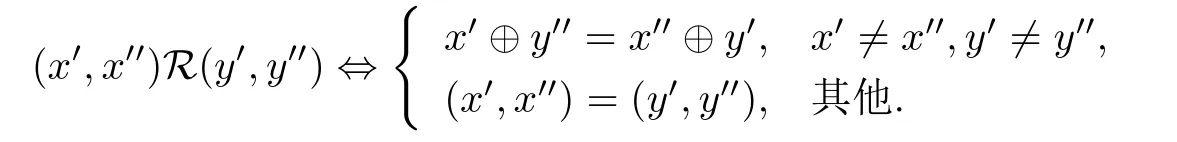
在S中,对任意t∈Rmax,称(t,-∞)=为正元素,(-∞,t)={(x′,t)|x′<t}为负元素,(t,t)={(t,t)}为平衡元素.记为所有正元素和零元的集合,是半域;记为所有负元素和零元的集合,由于对运算⊗不封闭,所以不是半域;记S•为所有平衡元素的集合具有吸收性.由此可知S⊕,S⊖和S•唯一公共的元素是零元(ε,ε).

对任意t∈Rmax,记S中的正元素(t,-∞)= t,负元素(-∞,t)=⊖t,平衡元素(t,t)= t•,则可用3⊖2代替(3,-∞)⊕(-∞,2),这样就有3⊖2 =(3,2)=(3,-∞)= 3.
设σ为{1,···,n}的任意置换,定义置换σ的符号为:
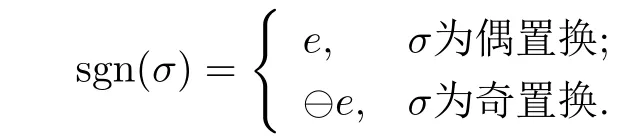
在S中,n×n矩阵A =(aij)的行列式为:

记为|A|或det(A).
在文献[3]中,设AT为矩阵A的转置矩阵,则det(A)= det(AT).元素aij的代数余子式记为cofij(A).以cofij(A)为元素作成的矩阵记为A♮,称A♮为矩阵A的伴随矩阵,其中(A♮)ij= cofji(A).行列式det(A)按照一行展开(出自文献[5])为

设A =(aij)n×m和B =(bij)m×n为S上的矩阵,矩阵之间的运算⊗定义为:
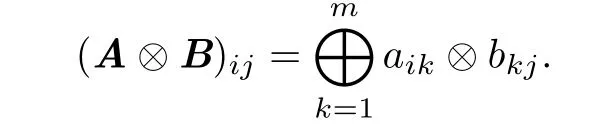
矩阵的乘法满足结合律.
n维行向量α=(a11,a12,···,a1n)与n维列向量β=(b11,b21,···,bn1)T作积,如果α⊗β= ⊕nj=1(a1j⊗bj1)最多只有一个非零积,则称它们的积是本征的.接下来,看一个向量本征积的例子:
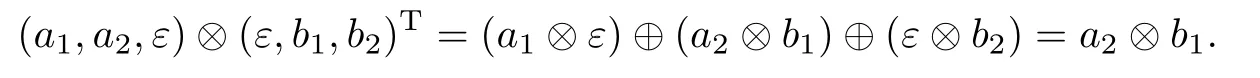
一般地,本征积不满足结合律.但是,如果矩阵A,B,C的积A⊗B⊗C中的每个元素(A⊗B⊗C)il=j,k(aij⊗bjk⊗ckl)最多只有一个非零元,则称矩阵的积A⊗B⊗C是本征的.如果其中矩阵的积A⊗B和B⊗C都是本征的,那么称矩阵的积A⊗B⊗C是完全本征的,并且对于多个(多于3个)矩阵的积同样适用.接下来,看一个矩阵本征积的例子:
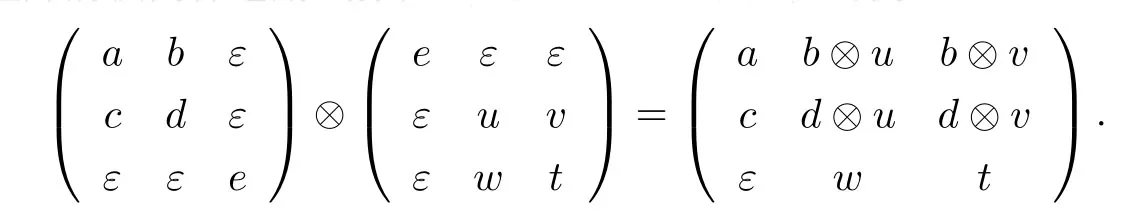
设C1,C2,···,Ct是S上级数分别为l1,l2,···,lt(li≥2;1≤i≤t)的方阵,满足n =- t + 1.定义n×n矩阵Gk(1≤k≤t)为

这里的I•是单位矩阵,pk= l1+ l2+···+ lk-1- k + 1,qk= n - pk- lk.
定义2.1对于{1,2,···,t}的任意置换(i1i2···it),称矩阵的乘积
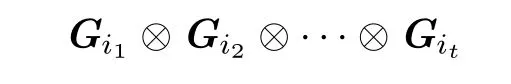
为S上互补基本矩阵.
引理2.1设Ck(1≤k≤t)是级数分别为li(li≥2;1≤i≤t)的方阵,定义n×n矩阵Gk(1≤k≤t)形如(1),则对于{1,2,···,t}的任意置换(i1i2···it),矩阵的乘积
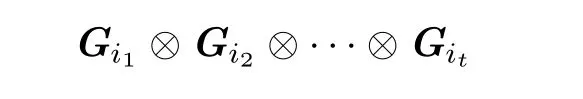
是完全本征的.
证用归纳法证明.
对于{1,2,···,t}的任意置换(i1i2···it),当t = 3时,结论显然成立.假设当t - 1(t>4)时结论成立,下面证明当t时结论也成立.
设1<it<t,矩阵Cit为

矩阵Cit去掉第1,lit行和第1,lit列后,剩下的元素按原来的次序所组成的(lit- 2)×(lit- 2)级矩
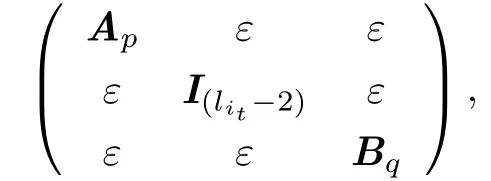
其中p +(lit- 2)+ q = n,lit- 2≥0.由归纳假设可知,Gi1⊗Gi2⊗···⊗Git-1是完全本征的. 设A =(aij),B =(bij),则Gi1⊗Gi2⊗···⊗Git-1⊗Git为
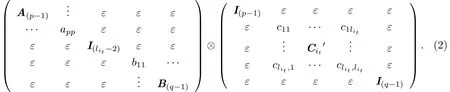
按照矩阵的乘法规则计算(2)式,可知(2)式左侧矩阵的任意行向量与右侧矩阵的任意列向量的乘积最多只有一个非零积,因此互补基本矩阵Gi1⊗Gi2⊗···⊗Git是完全本征的.
同理,当it= 1,t时结论仍然成立.定理得证.
定义2.2设A是n×n的矩阵,对N ={1,2,···,n}的子集S ={j1,···,js}来说,在矩阵A中选定j1,···,js行和j1,···,js列,位于这些选定行和列的交点上的s2个元素按原来的次序排列成的s级矩阵,称为矩阵A的一个主子矩阵,记为A[S].
§3 S上的Laplace定理
这一部分,给出了矩阵的余子式、代数余子式与k级子式的概念.并将证明S上的Laplace定理.
在文献[3]中,设矩阵A =(aij)为S上n×n矩阵,矩阵A的正行列式与负行列式分别定义为
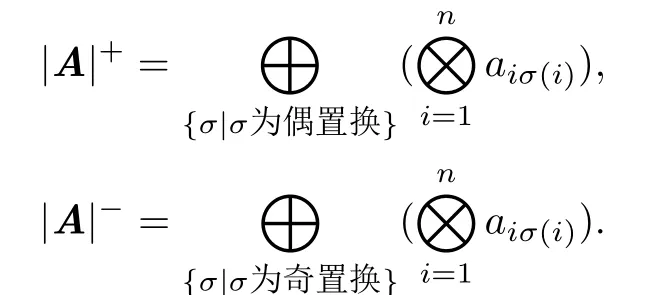
则|A| = |A|+⊖|A|-.
设Aij表示矩阵A去掉i行j列所得的矩阵,矩阵Aij的正代数余子式与负代数余子式分别定义为
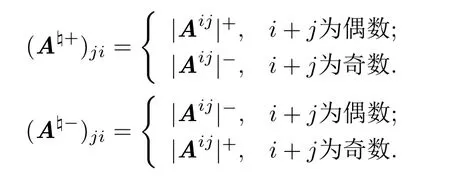
根据上述概念容易得到以下结论.
推论3.1设矩阵A =(aij)为S上n?×n矩阵,则
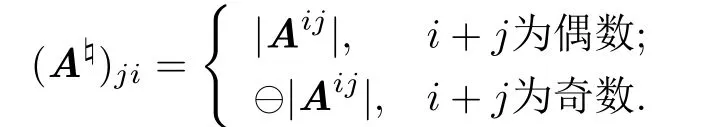
定义3.1设A =(aij)为S上n×n矩阵,称元素aij的余子式为|Aij|. |Aij|的前面加上符号

后称为元素aij的代数余子式cofij(A),即cofij(A)= N(i + j)|Aij|.
引理3.1设σ1,σ2为{1,···,n}的互不相交的两个循环置换,令τ=σ1σ2,则
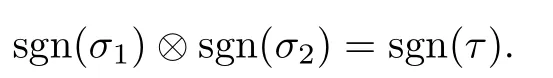
证不失一般性,假设σ1=(i1i2···ik),σ2=(j1j2···js)(k + s≤n)均为循环置换.由于每个置换都可以表示成若干个对换的乘积,则

因此sgn(σ1)= N(k - 1),sgn(σ2)= N(s - 1),然而,
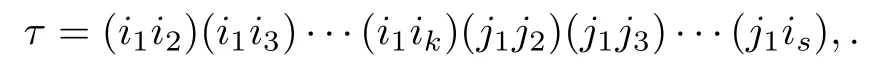
则sgn(τ)= N[(k - 1)+(s - 1)].所以不论k与s的奇偶性,均有sgn(σ1)⊗sgn(σ1)= sgn(τ).
引理3.2[3]设σ为{1,2,···,n}的任意置换,则|(uσ(1),···,uσ(n))| = sgn(σ)|(u1,···,un)|.
引理3.3[3]设矩阵A的转置矩阵为AT,则|A| = |AT|.
根据引理3.2和引理3.3可以直接得到如下结论.
推论3.2设A是S上的n×n矩阵,对换行列式|A|中两行(列)的位置得到行列式为|A′|,则|A| =⊖|A′|,即行列式的符号改变.
一般地,在矩阵A中任取k行和k列,位于这些选定的行和列的交点上的k2个元素按原来的次序所组成的行列式M,称为A的k级子式,记|AM|为M的余子式.
定义3.2设D的k级子式M在D中所在的行和列指标分别是i1,i2,···,ik;j1,j2,···,jk,则M的余子式|DM|前面加上符号N[(i1+ i2+···+ ik)+(j1+ j2+···+ jk)]后称为M的代数余子式,记为cofM(D).
引理3.4行列式|D|的任一子式M与它的代数余子式cofM(D)的乘积中的每一项都是行列式D的展开式中的一项,而且符号也一致.
证首先讨论k级子式M位于行列式|D|的左上方的情况.

这时M的代数余子式cofM(D)为
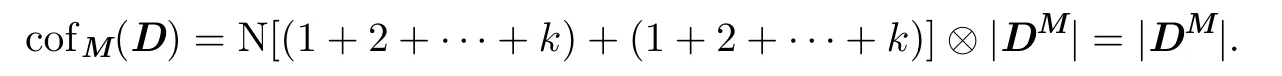
M的每一项可以表示为a1σ(1)⊗a2σ(2)⊗···⊗akσ(k),其中σ为{1,2,···,k}的一个置换,这一项前面所带的符号为sgn(σ). |DM|中每一项可以表示为ak+1,τ(k+1)⊗ak+2,τ(k+2)⊗···⊗anτ(n),其中τ为{k + 1,k + 2,···,n}的一个置换,这一项前面所带的符号为sgn(τ).而这两项的乘积是
a1σ(1)⊗a2σ(2)⊗···⊗akσ(k)⊗ak+1,τ(k+1)⊗ak+2,τ(k+2)⊗···⊗anτ(n),(3)
(3)式由置换στ确定,前面的符号是sgn(στ),因为置换σ与τ是互不相交的两个循环置换,根据引理3.1可知

因此(3)式是行列式|D|中的一项且符号相同.
接下来证明一般情况.设子式M在行列式|D|中所在的行和列指标分别为i1,i2,···,ik;j1,j2,···,jk,其中
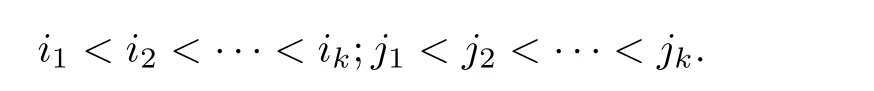
变化|D|中行和列的次序使M位于|D|的左上角.因此,先把第i1行依次与第i1-1,i1-2,···,2,1行对换,共经过i1- 1次对换将第i1行换到第一行.如此继续进行,则共经过了
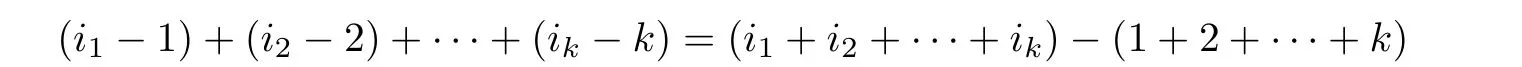
次行对换把第i1,i2,···,ik行依次换到第1,2,···,k行.
类似地,利用列变换将M的列换到第1,2,···,k列,则共经过
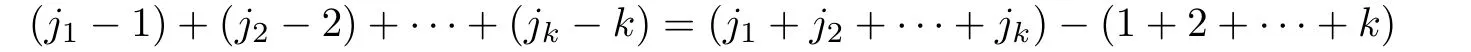
次变换.
用|D1|表示这样变换后得到的新行列式,根据推论3.2,可得
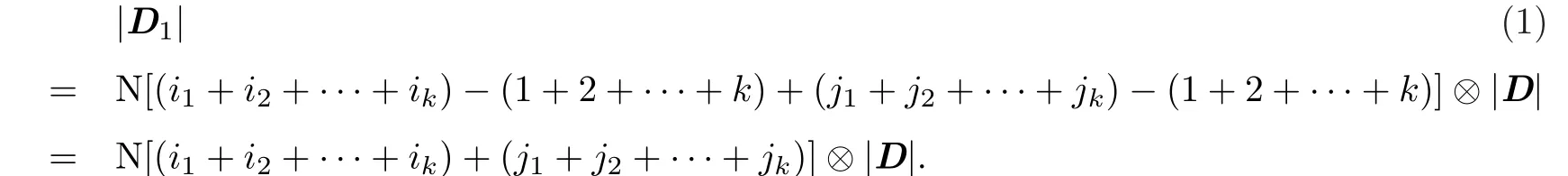
可以得出,|D1|和|D|的展开式中出现的项是一样的,只是每一项都差符号N[(i1+i2+···+ik)+ (j1+ j2+···+ jk)].
此时M已经位于|D1|的左上角,所以M⊗|DM1|中每一项都是|D1|中的一项且符号一致.但是
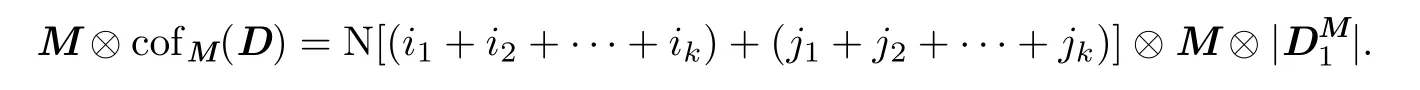
所以M⊗cofM(D)中每一项都与|D|中一项相等且符号一致.
定理3.1设在行列式|D|中任意取定k(1≤k≤n - 1)行.由这k行元素所组成的一切k级子式与它们的代数余子式的乘积的和等于行列式|D|.
证设在|D|中取定k行后得到的子式为M1,M2,···,Mt,其代数余子式分别为cofM1(D),cofM2(D),···,cofMt(D),只需证明
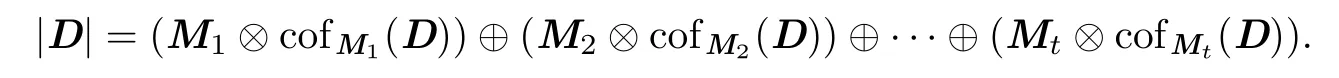
根据引理3.4,Mi⊗cofMi(D)中每一项都是|D|中一项且符号相同,并且Mi⊗cofMi(D)和Mj⊗cofMj(D)(i /= j)无公共项,所以只需证明等式两边项数相等.显然等式左边有n!项,而t = Ckn,则右边的项数为
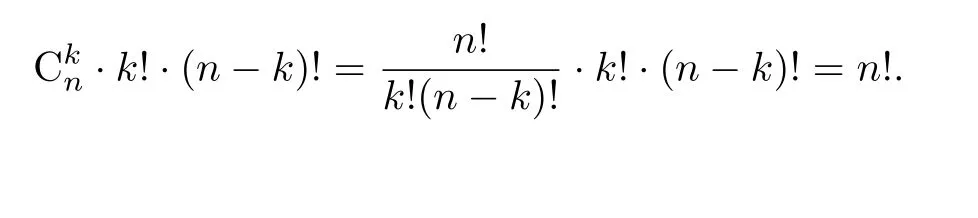
§4 互补基本矩阵的行列式
定理4.1设A0,B0是S上分别为k级,n - k + 1级方阵,且
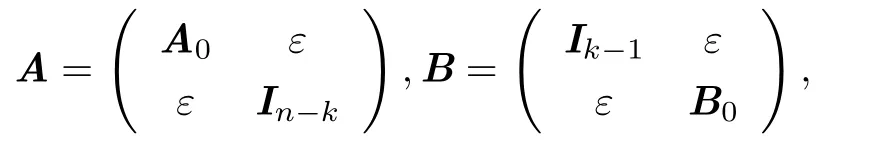
则det(A⊗B)= det(A)⊗det(B).
证设

则
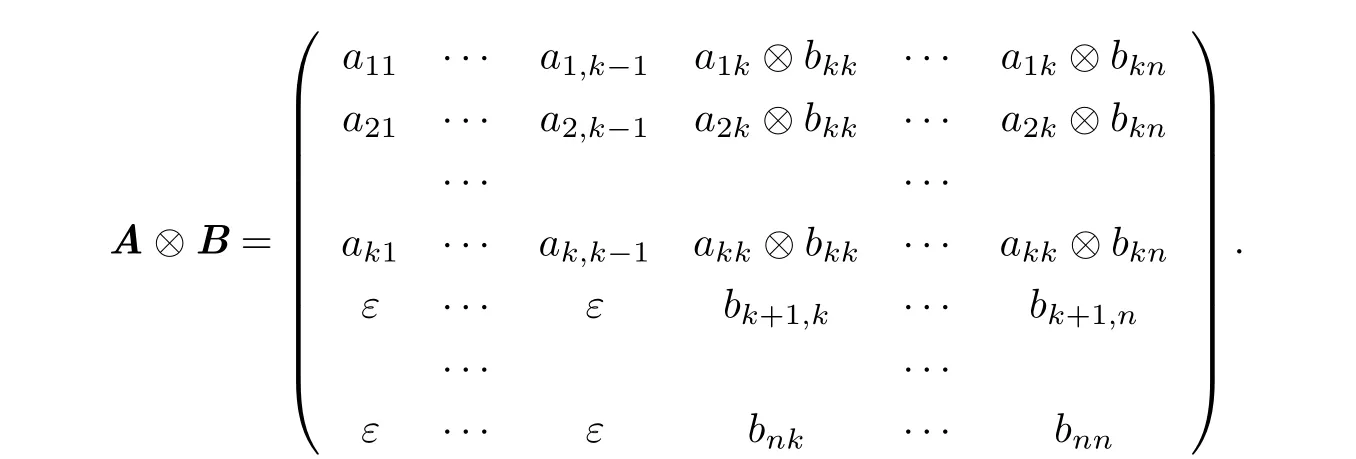
取det(A⊗B)的前k行,根据定理3.1

推论4.1设Ck(1≤k≤t)是级数分别为li(li≥2;1≤i≤t)的方阵,Gk(1≤k≤t)是形如(1)的n×n矩阵,则对于{1,2,···,t}的任意置换(i1i2···it)来说,
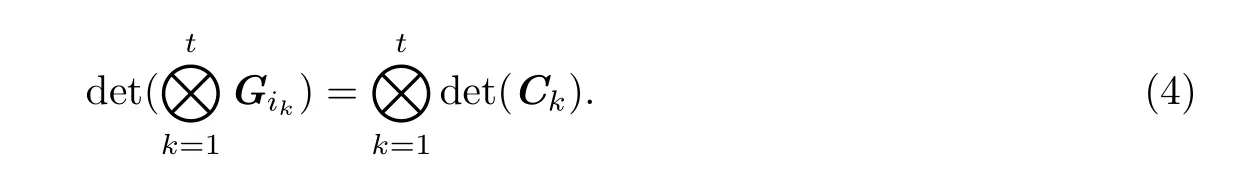
证用归纳法证明.
对于{1,2,···,t}的任意置换(i1i2···it),当t = 2时,由定理4.1可知,结论显然成立.假设当t - 1(t>3)时结论成立,下面证明当t时结论也成立.
事实上,当|i - k|>1时,有Gi⊗Gk= Gk⊗Gi.这意味着,在置换(i1i2···it)中,当1≺2(i≺j表示在置换中i位于j前)时,可以将G1移到第一个位置.设此时的互补基本矩阵由置换(j1j2···jt)(其中j1= 1)确定,则其余的t - 1个矩阵Gjk(k = 2,···,t)的乘积有如下形式
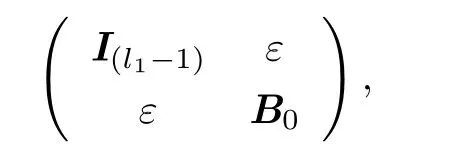
其中B0= Hj2⊗···⊗Hjt(Hjk= Gjk[{l1,···,n}]).由归纳假设可知,
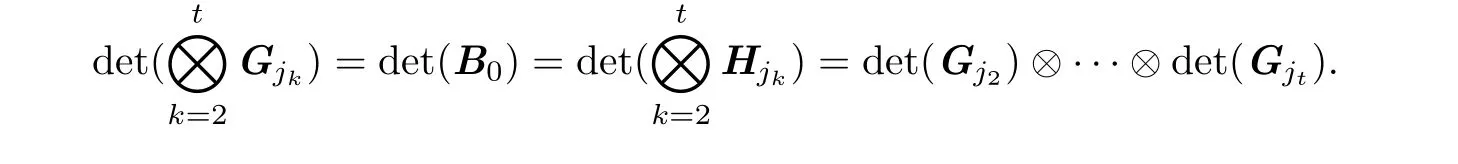
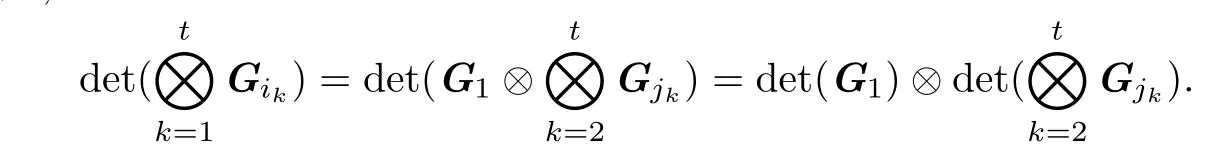
由定理4.1可知,由于det(Gk)= det(Ck),且S中的元素对运算⊗满足交换律,所以(4)式成立.
若2≺1时,可以将G1移到最后位置,再利用矩阵转置的性质,同理可以证明(4)式成立.
推论4.2设n≥2,Gk(1≤k≤t)是S上形如(1)的n×n矩阵,则对于{1,2,···,t}的任意两个置换(i1i2···it)和(j1j2···jt)来说,行列式det)的非零项与det的非零项一一对应,且相对应的项相等.
证由推论4.1可知,
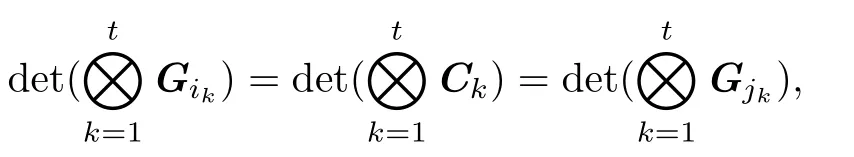
引理4.1设Gk(1≤k≤t)是S上形如(1)的n×n矩阵,若Gi1⊗Gi2⊗···⊗Git=(Aij),则

此结论根据Gk的构造方式和互补基本矩阵的完全本征性可以直接得到.
n≥2,Gk(1≤k≤t)是S上形如(1)的n×n阵,则对于{1,2,···,t}的任意置换(i1i2···it)来说,令Gi1⊗Gi2⊗···⊗Git= A =(Aij),G1⊗G2⊗···⊗Gt= B,则对于det(A)中确定非零项的任意置换σ来说,以下给出“定位法”,确定置换τ使在det(B)中确定相同的非零项.
注4.1
·设A是n×n矩阵,A的行列式det(A)中共有n!项,则每项都是由某个置换确定的矩阵中n
个位置的元素作⊗积所得,称det(A)中每一个不包括符号的非零项为基础项.
·定位法需要满足:对det(A)中确定非零基础项的任意置换σ,存在置换τ使在det(B)中确定相同的基础项,且sgn(σ)= sgn(τ).而确定非零基础项的置换要么是k阶循环置换(1≤k≤n),要么是由若干个互相没有共同数字的循环置换作乘积得到的循环分解(定位法中提到的置换均为{1,2,···,n}的某个置换).
定位法(不妨假设确定非零基础项的置换为k阶循环置换)
取确定det(A)中非零基础项的一个k阶循环置换σ=(j1j2···jk)(1≤k≤n),由此置换确定的det(A)中基础项是设为

且该基础项的符号为sgn(σ).
第1步将取定的基础项列表(注:第k(1≤k≤t)列的元素均属于Gik)
换句话说,基础项(5)式是表1中所有因子作⊗积.
第2步存在置换τ也为{j1,j2,···,jk}的某个k阶循环置换(原因如下).
在det(B)中,由引理4.1可知,置换τ确定的基础项一定包括Ajk+1jk+1,···,Ajnjn这n -k个元素,且一定不包括Aj1j1,Aj2j2,···,Ajkjk这k个元素.否则,若包括元素Ajsjs(1≤s≤k),则(5)式中也一定包括元素Ajsjs,这与置换σ为k阶循环置换矛盾.可知,在det(B)中存在置换τ为{j1,j2,···,jk}的某个k阶循环置换,从而sgn(σ)= sgn(τ).
第3步确定k阶循环置换τ.
由置换τ为{j1,j2,···,jk}的某个k阶循环置换,可知只需在主子阵B[{j1,···,jk}]中找到与表1的前k行完全相同的因子.由互补基本矩阵的完全本征性可知,表1的前k行因子确实出现在主子阵B[{j1,···,jk}]中.
按照以下步骤进行确定:
1.在主子阵B[{j1,···,jk}]中定出第i1个因子是ox1,ox2,···,oxk的元素,这样就可以找
到与表1的第一列的前k行完全相同的因子.假设定出了w1个元素,有k≤w1;为找到与(5)式相同的非零项,需要继续缩小范围.
2.在1中所找到的w1个元素中定出第i2个因子是py1,py2,···,pyk的元素,这样就可以找
到与表1的第二列前k行完全相同的因子.假设定出了w2个元素,有k≤w2≤w1;
3.以此类推,再根据第i3个因子,第i4个因子,···,第it个因子依次定位,由推论4.1和矩阵Gi(1≤i≤t)中元素位置的唯一性可知,最终可在主子阵B[{j1,···,jk}]中找到唯一属于不同行不同列的k个元素;
4.再加上n - k个元素Ajk+1jk+1,···,Ajnjn.

表1
根据以上步骤所找到的n个元素可以确定k阶循环置换τ使在det(B)中确定相同的非零项.
若确定det(A)中非零基础项的一个置换σ是由若干个互相没有共同数字的循环置换作乘积得到的循环分解,对于循环分解中的每一个循环按照以上的步骤进行确定后再作循环的乘积.
看一个例子.
例4.1令n = 4,l1= 2,l2= 2,l3= 2.对于

有
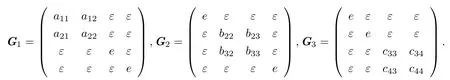
于是
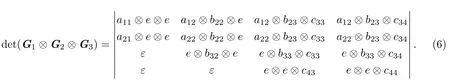
而

不妨假设(7)式中由置换(132)确定的项为非零项,可知该非零项为

且该项的符号为sgn(132)= e.为方便起见,可列表为

表2
设G1⊗G2⊗G3= A =(Aij).由引理4.1可知,置换σ确定的det(A)中基础项一定包括元素A44,且一定不包括元素A11,A22,A33.可知置换σ也为3阶循环置换,从而sgn(132)= sgn(σ)= e.
为找到3阶循环置换σ使在(6)式中确定相同的基础项,可按照以下四步进行: 1.在(6)式的主子阵A[{1,2,3}]的元素中定位出第1个因子是a12,a21,e的元素,定出四个元素A12,A13,A21,A32;
2.在1中所找到的四个元素中继续定位出第3个因子是e,e,c33的元素,定出四个元素

3.在2中所找到的四个元素中继续定位出第2个因子是b23,e,b32的元素,定出三个元素
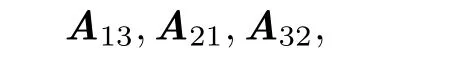
显然,它们是取自不同行不同列的三个元素;
4.再加上元素A44.
根据定出的四个元素A13,A21,A32,A44可以唯一确定置换σ=(132),使置换σ=(132)与行列式det(G1⊗G3⊗G2)中的置换(132)确定相同的非零项.
根据定位法的第2步可以直接得到如下结论.
推论4.3对于所有行列式det(Gi1⊗Gi2⊗···⊗Git)中某个相同的非零项来说,则确定该项的所有置换的区别为每个置换的循环中元素的排列顺序不同.
[1]Fiedler M,Hall F J. Max algebraic complementary basic matrices[J]. Linear Algebra Appl,2014,457: 287-292.
[2]Fiedler M,Hall F J. A note on permanents and generalized complementary basic matrices[J]. Linear Algebra Appl,2012,436: 3553-3561.
[3]Baccelli F,Cohen G,Olsder G J,et al. Synchronization and Linearity: an Algebra for Discrete Event System[M]. New York: John Wiley and Sons,1992.
[4]Fiedler M,Intrinsic products and factorizations of matrices,Linear Algebra Appl,2008,428: 5-13.
[5]Max Plus. Linear systems in(max,+)algebra[A]. In: Proceedings of the 29-th Conference on Decision and Control IEEE[C]. 1990,151-156.
MR Subject Classification: 15A15;15A57
Complementary basic matrices of the symmetrized algebra of max algebra
YUAN Yue-shuang1,ZHANG Zi-long1,2
(1. College of Mathematics and Information Science,Hebei Normal University,Shijiazhuang 050024,China;
2. Key Lab of Computational Mathematics and Applications of Hebei Province,Shijiazhuang 050024,China)
The paper mainly studies the complementary basic matrices in S. It first introduces the concepts of the intrinsic products and proves the Laplace's Theorem in S. Accordingly,the determinants of CB-matrices are the same and for any nonzero term in the determinant of one CB-matrix,there exists an equal term in the determinant of the other CB-matrix and vice versa. By the same time,for a given permutation which determines the nonzero term of the determinant of one CB-matrix,a method is given to find a permutation who determines the same nonzero term in the determinant of the other CB-matrix.
max algebra;symmetrized algebra;complementary basic matrices;Laplace's Theorem;determinant
O151.21;O151.22
A
1000-4424(2016)01-0116-11
投稿日期:2015-04-292016-01-27
国家自然科学基金(11271109)
