基于抽样的不确定性及敏感性分析的方法在核电厂水膜蒸发试验误差分析中的应用
2016-06-29扈本学王国栋王章立倪陈宵张今朝上海核工程研究设计院上海200233
扈本学,王 喆,王国栋,王章立,倪陈宵,张今朝,杨 萍(上海核工程研究设计院,上海 200233)
基于抽样的不确定性及敏感性分析的方法在核电厂水膜蒸发试验误差分析中的应用
扈本学*,王喆,王国栋,王章立,倪陈宵,张今朝,杨萍
(上海核工程研究设计院,上海200233)
摘要:与传统的误差分析方法相比,基于抽样的不确定性及敏感性分析具有较大的优势。本工作通过耦合DAKOTA程序和水膜蒸发试验数据分析程序,开发了水膜热态试验误差分析方法,计算得到了试验目标参数水膜蒸发换热乘子的不确定性范围,并且分析了试验测量参数的不确定性对蒸发换热乘子不确定性的影响。计算结果表明,水膜入口流量、入口风速以及平板表面温度是主要的不确定性来源。这为优化试验测量系统,减小试验误差提供了定量支持。该方法可以用于其他试验误差分析以及参数重要性分析。
关键词:sobol方法;试验误差分析;敏感性分析;水膜蒸发试验
试验误差分析是试验数据分析中的重要一环,试验的误差范围反映了试验结果的精度,直接影响试验的成败与质量。传统的试验误差分析主要应用误差传递的方法,根据直接参量、参数的误差范围,通过误差传递公式推导,获得试验目标值的误差。当试验目标值的计算公式比较复杂时,采用该方法推导目标值的误差较为困难。
不确定性分析和敏感性分析是分析复杂系统的重要工具[1]。不确定性分析研究输入参数的不确定性通过模型传播到模型输出;而敏感性分析研究模型输入的不确定性对模型输出不确定性的贡献率。主要分析思路:根据输入参数的不确定性分布进行随机抽样,获得输入参数的不同组合(一个参数组合称为一个抽样工况),然后对每一个抽样工况进行计算,获得输出参数,最后进行统计分析,获得输出参数的不确定性分布以及相关的敏感性度量参数。
该方法目前已经在核电厂事故安全分析方面得到应用,主要用于验收准则参数的不确定性分析及参数重要性评价。Gertman等人应用RELAP-3D程序,计算获得了大破口失水事故峰值包壳温度与各输入参数之间的相关系数,定量评价了各个输入参数的重要性[2-3]。基于不确定分析的方法,AREVA公司开展了大破口失水事故后核电厂安全壳压力响应的不确定性分析,并利用计算得到的相关系数,分析了影响安全壳压力的各输入参数的重要程度[4]。近年来,在反应堆工程领域,我国业内人士也陆续开展了基于抽样的不确定性及敏感性分析的工作,包括:熔盐堆参数的不确定性分析[5]、大破口失水事故后质能释放参数敏感性分析[6]、设计基准事故后安全壳压力响应的敏感性分析[7]以及钠冷快堆事故不确定性分析等[8]。
本工作将基于随机抽样不确定性分析及敏感性分析的方法引入试验的误差分析中,以水膜蒸发换热乘子为试验目标值,通过对试验的直接测量参数进行抽样,计算获得试验目标值,然后进行统计分析,获得试验目标值的误差带,并利用计算的Sobol敏感度系数来判断试验目标值的主要误差来源。
1 基本理论
1.1容许区间与Wilks公式
应用随机抽样方法进行不确定性分析时,往往需要确定抽样次数,使得输出参数满足特定置信度和特定概率的要求。
假设输出参数为一系列输入参数的函数:y=f(x1,x2,…,xN),其概率分布函数为g(y)。进行N次抽样,可以计算得到因变量y的一个样本{y1,y2,…,yN}。则可以确定两个函数L=L(y1,y2,…,yN),U=U(y1,y2,…,yN),使得:
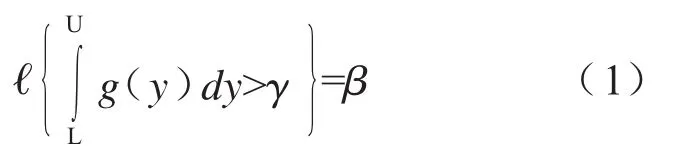
其中,β为置信水平,γ为概率比率,[L,U]为容许区间。公式(1)表示的意义如下:随机变量y的m次计算结果有一定分布,即在置信度为β时,计算结果落入区间[L,U]的次数占总计算次数m的概率比率大于γ,对于安全分析,希望β和γ的值尽可能高。对于给定的β和γ,确定随机抽样的次数m后,便可以确定满足式(1)的容许区间[L,U]。
对于函数y=f(x1,x2,…,xN),用Wilks公式[9],即采用随机抽样加排序统计方法来确定相应的容许区间。假设y1,y2,…,yN为N次独立的随机函数y的输出,其概率密度分布函数g(y)是连续的。将y1,y2,…,yN按升序排列,定义y(k)为序列中的第k个值,可以得出:y(1)= min(yk),y(N)=max(yk)。
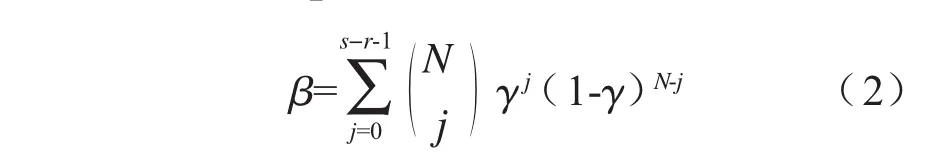
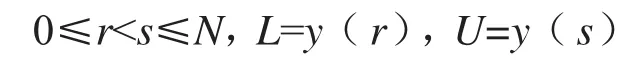
若取最大值和最小值作为双侧容许区间,其置信水平为:
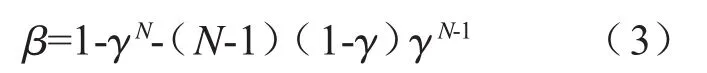
若取最大值作为单侧容许区间,则其置信水平为

对于自变量与因变量的任意函数关系,Wilks公式都可以保证容许区间满足相应的β 和γ。
根据Wilks公式,根据输入参数的概率密度分布,通过随机抽样可以确定93组状态点,通过函数关系式可以计算得到输出函数y=f(x1,x2,…,xN)的样本(y1,y2,…,y93)。假设样本的最大值为ymax,最小值为ymin,则满足两个95%的双侧容许区间为[ymin,ymax]。其物理意义为在置信度为95%时,输出函数y所有计算结果中落入区间[ymin,ymax]的概率大于95%。因此,对于水膜热态试验误差分析,应用93次随机抽样,可以获得满足两个95%的试验目标参数的上下限。
1.2Sobol方法
Sobol[10,11]方法是最代表性的全局参数敏感性分析方法,基于模型分解思想,得到输入参数一、二次甚至更高次的敏感度。国内学者已开始将Sobol方法用于参数的重要性分析。文献[12]通过比较各因素对换热网络的一阶灵敏度及总灵敏度,甄别出对换热网络系统运行影响较大的因素以及影响较小但存在交互影响的因素。文献[13]用Sobol方法开展了水文模型参数敏感性分析。
Sobol方法一共包含两个指数,主要敏感度系数Si和总敏感度系数Ti。其主要理论依据如下[14]:
假定y=f(x)(x1,x2,…,xn),并且xi服从[0,1]均匀分布,且f2(x)可积,则函数f(x)(可以分解为:
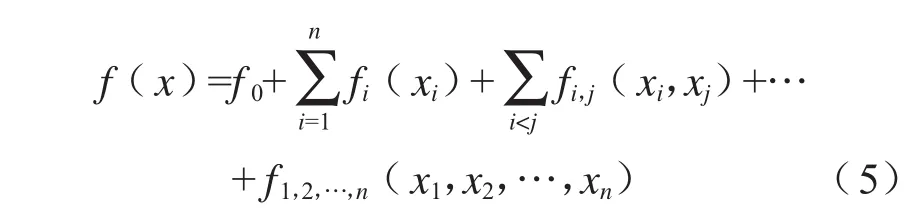
则模型的方差D也可以分解为单个参数和每个参数的影响:

对上式归一化,令:
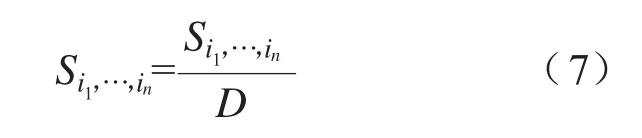
称为Sobol敏感度系数。Si称为一阶敏感度系数,又称为主要敏感度系数;S1,2,…,n称为n阶敏感度系数。总敏感度系数的计算公式为:

其中,主要敏感度系数Si体现了单个输入参数的不确定性对输出参数方差的贡献程度,全部敏感度系数Si体现了单个输入参数不确定度以及该参数与其他参数的相互作用对输出参数方差的贡献程度。当Si与Ti的值差距较大时,说明因素的交互作用明显。
2 水膜热态试验
2.1试验简介
由于CAP1400安全壳尺寸较AP1000有所增大,反应堆核功率和设计基准事故(Design Basis Accident,简称DBA)后安全壳的峰值压力也有所增大,为了在更大范围内充分验证CAP1400安全壳分析程序水膜蒸发关系式的适用性,设立了重大专项非能动安全壳冷却系统(Passive Containment Cooling System,简称PCCS)水膜热态试验。非能动安全壳冷却系统水膜热态试验的核心目标是在CAP1400非能动安全壳冷却系统系统运行参数范围内验证目标经验关系式,并且通过试验验证水膜蒸发传热传质关系式包络因子的保守性。
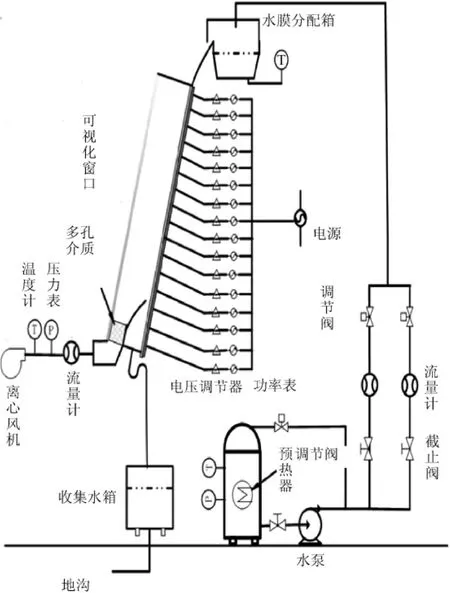
图1 水膜热态试验示意图Fig.1 Sketch of heated flat plate test
试验台架如图1所示。试验本体由加热平板、两个侧壁以及透明的有机玻璃罩组成。加热平板采用不锈钢平板,并安装玻璃罩形成矩形风道和水道。矩形通道的宽度为1.183 m,高度为0.285 m,总长度为7.3 m。板后铺设了加热铜管,通入流动的导热油为试验提供所需热源,被加热铜管覆盖的平板长度为5 m。试验本体的表面粘有热流密度计,用以测量平板表面温度以及热流密度。试验中需要测量的参数有:入口冷却水和空气的流量及温度,不同位置处水膜的流速、温度、宽度(覆盖率)、厚度,不同位置处空气的流速、温度、湿度,不同位置处的平板温度、表面热流密度,平板倾斜角度等。
2.2目标关系式验证
平板水膜蒸发试验的目的是验证水膜与空气之间的传质关系式符合相关目标经验关系式。对于目前应用的WGOTHIC分析程序,应用以下的方法来预测水膜蒸发传质系数。
当主流气体中的蒸汽浓度和液体表面的蒸汽浓度不相等时,它们之间就会发生质量传递。蒸汽的浓度梯度指的是主流气体中和液体表面的蒸汽分压的差值。如果主流气体中的蒸汽浓度高于液体表面的蒸汽浓度,就会发生冷凝;如果液体表面的蒸汽浓度高于主流气体中的蒸汽浓度,就会发生蒸发。
类似于对流换热过程,可以引出以下公式:

式中,Gevap.是蒸发/冷凝质量流量,kg是传质系数,Mv是蒸汽的分子量,Pv,surf.是液体表面的蒸汽分压,Pv,bulk是主流气体中的蒸汽分压。
舍伍德数(Sh)是反映传质系数的无量纲数,类似对流换热的努赛尔数(Nu)定义为:
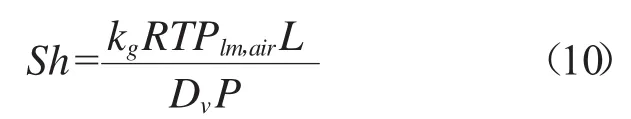
式中,R是摩尔气体常数;T是边界层温度,取主流体温度和液膜温度的平均值;L是特征长度;P是总压;Plm,air是空气对数平均分压;Dv是蒸汽在空气中的扩散系数。Plm,air、Dv分别由式(11)和(12)计算:
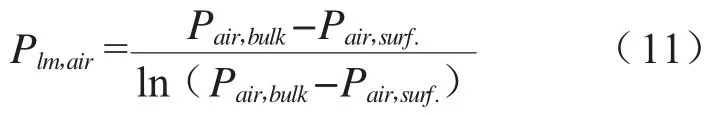
式中,Pair,bulk是主流气体中空气分压,Pair,surf.是液膜表面处空气分压。
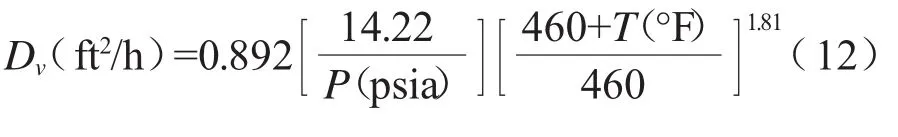
式中,T(°F)为主流温度和液膜温度的平均值,P(psia)为主流气体的总压。对于传热关系式,用Sh代替Nu、用施密特数(Sc)代替普朗特数(Pr)可以转换成传质关系式,得到以下关系式:
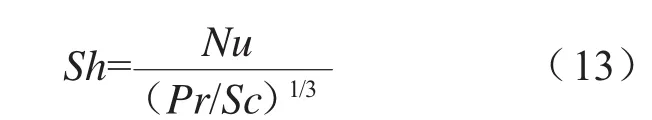
式中,Sc=v/Dv,v为运动粘性系数;Nu数采用以下公式计算:
逆浮升力方向对流换热关系式:

顺浮升力方向对流换热关系式:

式中,
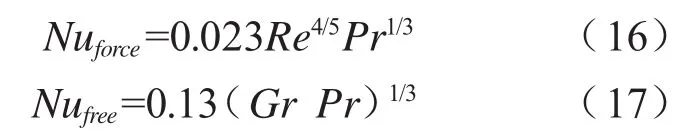
式中,Re为雷诺数,Gr为表征自然对流强度的格拉晓夫数。
对于本试验,浮升力方向与空气运动方向相同,属于顺浮升力方向混合对流换热,因此,选取顺浮升力方向对流换热关系式。
应用试验测量的水膜蒸发率,并应用公式(8)~公式(12),可以得到试验的传质舍伍德数Shmeas。而应用试验的Sc、Pr、Re数值,应用公式(13)可以获得预测得到一个舍伍德数Shpred。
定义蒸发因子为:Shmeas/Shpred。对于本试验,核心的目标是获得每个试验工况的蒸发因子。进行误差分析即获得蒸发因子的不确定性范围,因此进行不确定性分析和敏感性分析时目标值(输出参数)为蒸发因子。
3 分析方法
DAKOTA程序是美国圣迪亚国家实验室开发的最优化、参数估计、不确定性分析及敏感性分析程序。该程序拥有强大的接口能力,可与其它计算程序耦合连接[12]。对于水膜热态试验的误差分析,应用DAKOTA程序耦合水膜热试验数据分析程序实现蒸发因子的不确定性及敏感性分析。
应用DAKOTA程序耦合水膜蒸发因子计算程序,开发了水膜热态试验不确定性分析及敏感性分析的工具。如图2所示:DAKOTA程序根据单个试验工况的试验测量参数(抽样参数)及其不确定性分布进行随机抽样,获得了N个输入参数的组合,每个参数组合代表一个计算工况;然后DAKOTA程序调用水膜热态试验数据程序分别计算获得每一个抽样工况的蒸发因子,并将其返回DAKOTA程序;最终应用DAKOTA程序统计分析计算结果。
应用抽样方法进行敏感性分析及不确定分析时,首先需要确定抽样变量及其不确定性分析,根据试验测量结果,一共选取13个测量参数作为抽样参数,其测量误差见表1。表1中最后一列给出了误差类型,“绝对”表示给出是参数的实际误差,而“相对”表示给出的是参数的实际误差/名义值。通过抽样获得各个参数误差,然后根据误差类型,将该值或该值与名义值的乘积与名义值相加即可得到该抽样工况的参数值。
根据Wilks公式,对于不确定性分析,对每个试验工况应用蒙特卡罗抽样93次,计算结果获取的蒸发因子的最大值和最小值就是获得满足两个95%的试验目标参数的上下限值。而对于蒸发因子的敏感性分析,根据要求[15],抽样次数应为N×(M+2),N至少为几百乃至上千,M为抽样变量的数目。分析中应用蒙特卡罗抽样,抽样次数为5 000×15,统计获得输入参数(试验测量参数)的总的Sobol敏感度系数Ti。
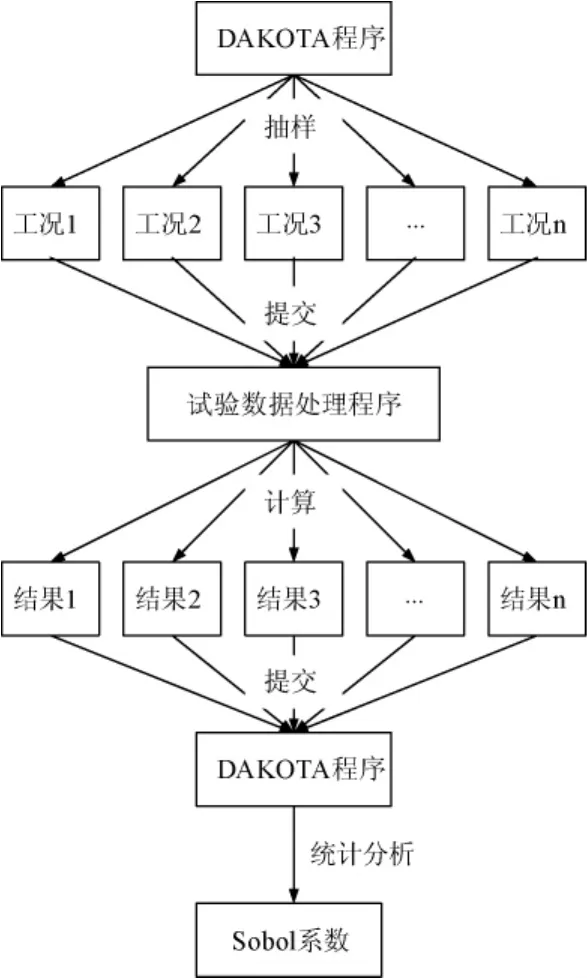
图2 程序耦合流程Fig.2 Flow Chart of code coupling
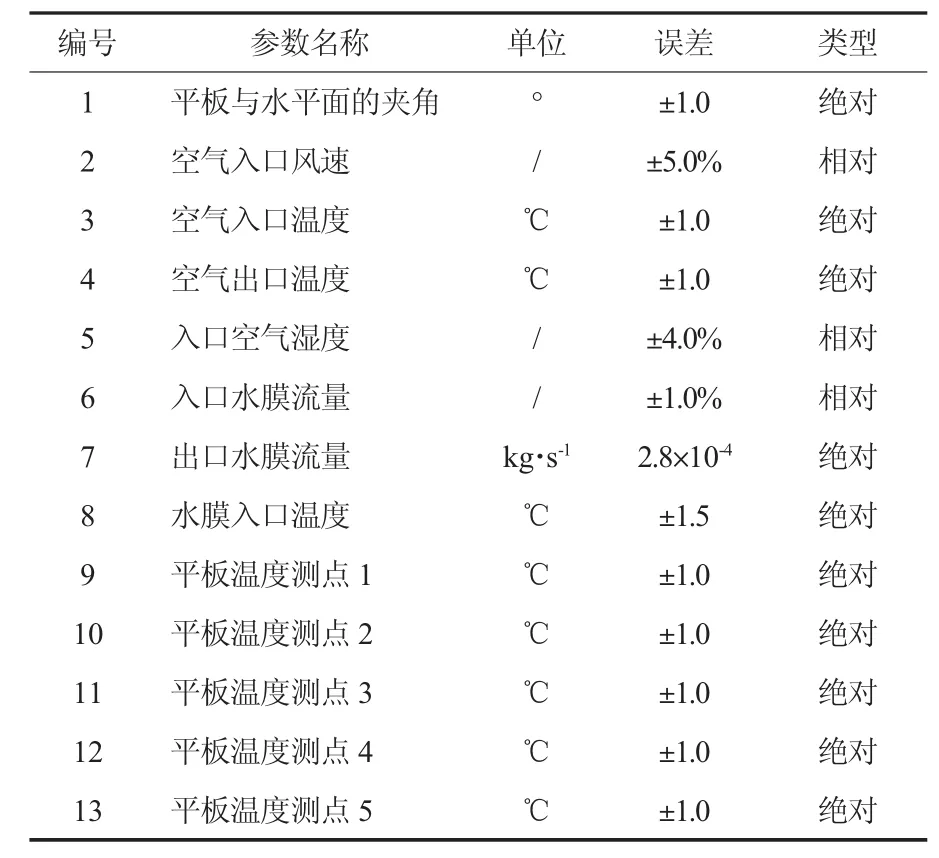
表1 测量参数的测量不确定性Table 1 Uncertainty of measured parameters
4 计算结果
图3给出了水膜热态试验5个试验工况的蒸发因子的不确定性分析结果。图中最大值、最小值对应该工况下93个抽样计算蒸发因子的最大值和最小值,而名义值代表的是应用试验各测量参数的名义值进行计算获得的蒸发因子。可以得出:
(1)各个试验工况蒸发因子的名义值偏离1.0很小,最大偏差大约为0.2,说明目标关系式可以较好的模拟水膜蒸发换热。
(2)考虑各工况测量参数的不确定性以后获得的蒸发因子的上下限值与名义值的最大相对偏差低于10%,说明试验目标值的不确定性较小,试验精度较高。
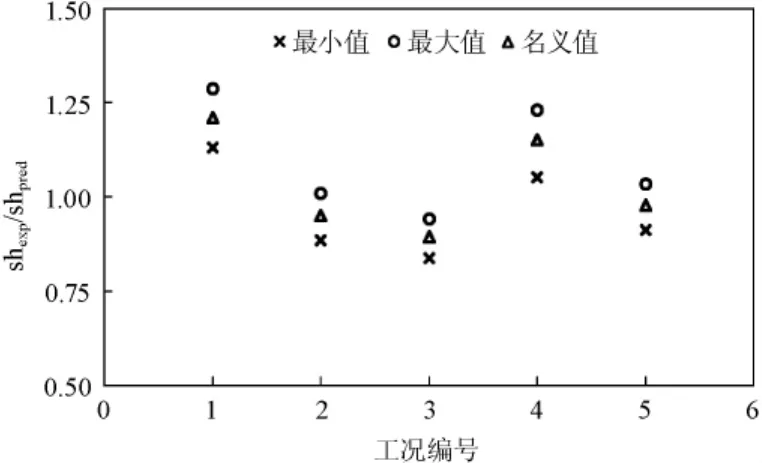
图3 蒸发因子的不确定性上下限值Fig.3 Upper and lower limits of evaporation ratio uncertainty
图4~图8分别给出了5个试验工况中各测量参数的总的Sobol敏感度系数Ti的值,可以得出:虽然影响各个工况的Ti值不尽相同,但综合评价Ti较大的参数为:水膜进、出口流量、5个平板温度测点以及入口风速。工况2中入口风速的不确定性对蒸发因子影响很小的原因是该工况风速的名义值大约为1.9 m·s-1,位于自然对流区,风速对程序预测的蒸发量没有影响,因此对蒸发因子的值影响很小。
图9给出了5个工况各测量参数的总的Sobol敏感度系数Ti的平均值。根据图8的结果,评价水膜热态试验误差中最重要的来源(超过1%)是:水膜入口流量、入口风速以及平板温度测点1~5。
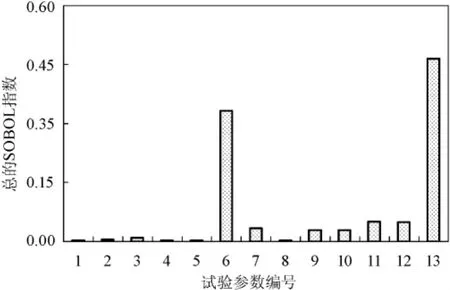
图4 试验工况1的总敏感度系数Fig.4 Total sensitivity coefficients of Test 1
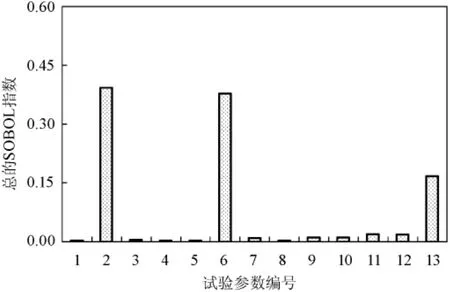
图5 试验工况2的总敏感度系数Fig.5 Total sensitivity coefficients of Test 2
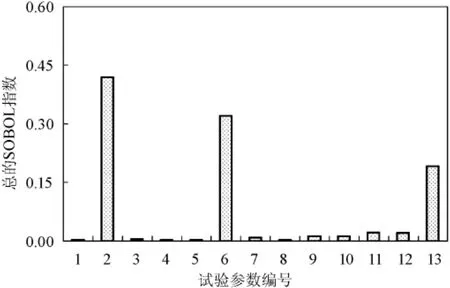
图6 试验工况3的总敏感度系数Fig.6 Total sensitivity coefficients of Test 3
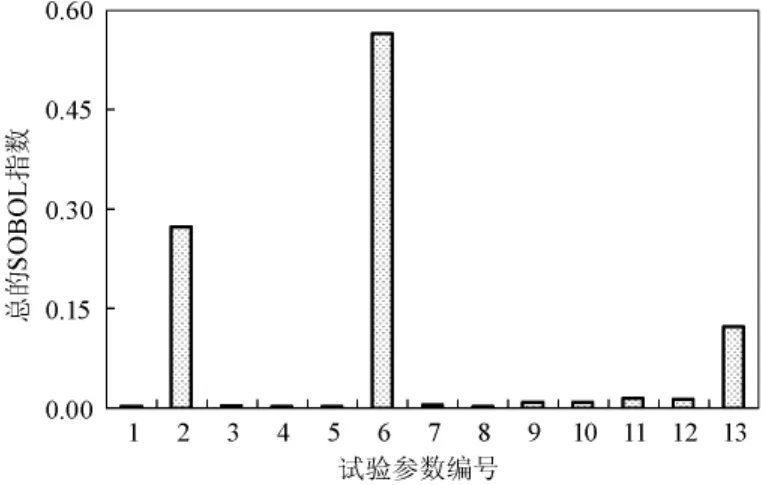
图7 试验工况4的总敏感度系数Fig.7 Total sensitivity coefficients of Test 4
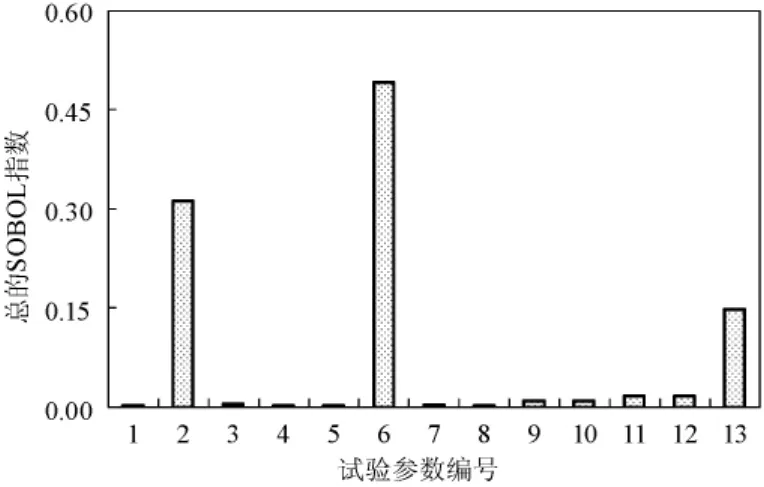
图8 试验工况5的总敏感度系数Fig.8 Total sensitivity coefficients of Test 5

图9 5个试验工况的总敏感度系数平均值Fig.9 Average total sensitivity coefficients of 5 tests
5 结论
本工作应用DAKOTA程序耦合水膜热态试验处理程序,开展了基于抽样的水膜热态试验蒸发因子的不确定性及敏感性统计分析。分析结果表明:水膜热态试验的误差控制较好,水膜热态试验获得蒸发换热因子的不确定性较小,试验精度较高;水膜热态试验的误差主要来源为水膜入口流量、入口风速以及平板温度测量。该方法提供了一种用于确定试验数据的不确定性及不确定性来源的方法,分析结果可以为试验测量系统的优化提供支撑。
参考文献
[1]J. C. Helton and F. J. Davis. Illustration of Sampling-Based Methods for Uncertainty and Sensitivity Analysis[J]. Risk Analysis,2002,22(3):591-622.
[2]Idaho National Laboratory. Uncertainty Analysis for RELAP5-3D[R]. Idaho:Idaho National Laboratory,2011.
[3]Idaho National Laboratory. Uncertainty Analysis of RELAP5-3D[R]. Idaho:Idaho National Laboratory,2012.
[4]Jamal M. Abdelghany,Robert P. Martin. Uncertainty Analysis for Containment Response of U.S. EPR?Reactor to Large Break Loss-of-Coolant Accidents[C]. Sanhigeo:Proceedings of ICAPP '10,2010:1395-1409.
[5]王成龙,Lin-wen Hu,秋穗正,等.可移动式熔盐冷却高温堆(TFHR)热工水力特性不确定性分析[C].北京:第十四届热工流体会议论文集,2015.
[6]扈本学,王喆,王国栋,等.应用DAKOTA程序耦合WCOBRA/TRAC程序进行大破口失水事故质能释放参数敏感性分析[C].北京:第十四届热工流体会议论文集,2015.
[7]王国栋,王喆,扈本学,等.应用DAKOTA程序耦合WGOTHIC程序进行安全壳压力响应敏感性分析[C].北京:第十四届热工流体会议论文集,2015.
[8]岳倪娜,马在勇,蔡容,等.钠冷快堆事故不确定性分析[C].北京:第十四届热工流体会议论文集,2015.
[9]Wilks S S. Determination of sample sizes for setting tolerance limits[J]. The Annals of Mathematical Statistics,1941,12 (1):91-96.
[10]Sobol IM. Sensitivity analysis for non-linear mathematical models[J]. Math Modeling Comput Exp,1993(1):407-414.
[11]Homma T,Saltelli A. Importance measures in global sensitivity analysis of nonlinear models[J]. Reliability Engineering and System Safety,1996,52(1):1-17.
[12]张红晶,吉海涛,谭世语,等.基于Sobol'法的换热网络全局灵敏度分析[J].世界科技研究与发展,2012,34(6):916-919.
[13]任启伟,陈洋波,周浩澜,等.基于Sobol法的TOPMODEL模型全局敏感性分析[J].人民长江,2010,41(19):91-107.
[14]V. Gregory Weirs,James R. Kamm,Laura P. Swiler,et al. Sensitivity analysis techniques applied to a system of hyperbolic conservation laws[J]. Reliability Engineering and System Safety,2012,107(12):157-170.
[15]Dakota,a multilevel parallel object-oriented framework for design optimization,parameter estimation,uncertainty quantification,and sensitivity analysis,akota user's manual[M]. Sandia National Laboratories,Version 5.3.1,2013.
Aplication of the Sampling-Based Uncertainty and Sensitivity
Analysis Method in Error Analysis of Heated Flat Plate Test at NPP
HUBenxue,WANGZhe,WANGGuodong,WANGZhangli,NIChenxiao,ZHANGJinzhao,YANGPing
(Shanghai Nuclear Researchand Design Institute,Shanghai200233,China)
Abstract:Compared with traditional error analysis methods,uncertainty and sensitivity analysis based on sampling has great advantages. Method for error analysis of heated flat plate test has been developed by coupling DAKOTA code and data evaluation program. Uncertainty of evaporation ratio has been calculated and effects of measured parameters uncertainty on evaporation ratio have been analyzed. The calculated results show that inlet film flow rate,inlet air flow velocity and plate surface temperatures are the main sources of the uncertainty,which provide support for measure system optimization to reduce the error range. This method could be applied to the error analysis for other tests and parameters importance analysis.
Keywords:Sobol method;test error analysis;sensitivity analysis;heated flat plate test
中图分类号:TL364
文章标志码:A
文章编号:1672-5360(2016)01-0084-06
收稿日期:2015-10-08修回日期:2015-11-23
基金项目:国家科技重大专项,项目编号2011ZX06002-0056
作者简介:扈本学(1986—),男,山东潍坊人,工程师/博士,反应堆热工,现主要从事反应堆安全分析及非能动安全壳分析工作
*通讯作者:扈本学,E-mail:hubenxue@snerdi.com.cn
