嵌入背景 自主建构——“等量关系”教学实录与评析

执教/李培芳 评析/陈梅开

嵌入背景 自主建构
——“等量关系”教学实录与评析

执教/李培芳 评析/陈梅开

【教学内容】

北师大版教材四年级下册第五单元“认识方程”中的“等量关系”。

【教学过程】

一、制造冲突，聚焦“数量关系”

（课件出示问题：鸡的质量是2千克，鹅的质量是6千克，求鸭的质量）

师：请同学们在练习本上解决这个问题。

（学生独立解答）

师：算出结果的举手，（约10多个学生）说说你的想法。

生：我是用6+2=8（千克）。

生：鸭没有那么重，我是用6-2=4（千克）。

生：这个问题没办法解决，因为鸭的质量与鸡和鹅的质量有什么关系没有告诉我们。

（大部分同学附和：没法算）

生：还要给我们一些提示。

评析：学生对这个问题的思考是有积极意义的：其一，让学生感受到条件有时未必是恰好的；其二，将学生的思考聚焦到数量的“关系”上。

二、辨别比较，引入“等量关系”

师：需要给一些什么提示呢？

生：已知鸡的质量、鹅的质量，它们和鸭的质量有什么关系？

师：我们一起来看看下图，是否提供了它们的关系呢？

（课件出示下图）

师：这个关系谁看懂了？

生：鹅的质量比鸭的质量重。

师：是的，静静地思考，现在能算吗？

生：不能，这样的关系只能知道鸭的质量小于6千克，小于6的数还有好多个呢。

师：这个关系呢？

（课件出示下图）

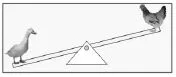
生：这个也不行。

师：（结合手势）这样的关系不行，那样的关系也不行，你们到底想要什么样的关系？能用手比画一下吗？

生：（众说纷纭比画着）要平衡，要平等的关系，要相等的关系。

师：我们来看看有没有这样的关系。

（课件出示下图）

师：看来电脑碰到难题了，同学们帮电脑写一个相等关系吧。

（教师提供如上图的学习卡片让学生创造等量关系）

评析：学生对数量关系的感知经历了从数量间“没有关系”到“有关系”，从数量间“不等关系”到数量间的“相等关系”。经由这样的学习过程，一方面学生通过比较建构起“等量关系”的概念，另一方面通过辨别感受了“数量相等关系”对于解决问题的价值。

三、自由创造，感知“等量关系”

（学生展示汇报如下）

生 1：左边放 1只鸭，右边放2只鸡。这样鸭的质量就是4千克。

生 2：左边放 2只鸭，右边放1只鹅。这样鸭的质量就是3千克。

生3：左边放1只鸭和1只鸡，右边放1只鹅。这样鸭的质量就是4千克。

......

师：真好，同学们找到了很多不同的关系。看来，这样的关系在解决数学问题时是很重要的。

生：对，是必不可少的。

师：是啊，在解决问题时，我们不仅要知道已知的数量和要求的数量，同时还要知道未知量和已知量的相等关系。像这种数量之间相等的关系在数学上称为“等量关系”。

评析：本环节设计了“创造等量关系”的活动，在创造活动中学生自然而然地将已知量与未知量放在一个相等的关系中。尤为可贵的是生3创造的等量关系，将未知量与已知量同时放在左边，这已然是代数思维了。通过自由创造活动，学生对等量关系的本质意义有了较为深刻的理解。

四、自主尝试，表示“等量关系”

师：既然等量关系这么重要，那么，我们就要学会在问题解决中找出等量关系。请同学们找一找，哪一句话反映出了数量间相等的关系。

（课件出示下面3道题）

（1）妈妈的体重是50千克，爸爸的体重是妈妈的2倍，求爸爸的体重。

（2）妈妈35岁，爸爸的年龄比妈妈大3岁，爸爸几岁？

（3）爸爸的收入比妈妈的2倍多 500元，妈妈的收入是3000元，爸爸的收入是多少元？

生：第（1）题“爸爸的体重是妈妈的2倍”反映出数量间相等的关系。

生：第（2）题“爸爸的年龄比妈妈大3岁”反映出数量间相等的关系。

生：第（3）题的等量关系是“爸爸的收入比妈妈的2倍多500元”。

师：第（3）题的等量关系，你是怎么理解的？能不能把你对这个等量关系的理解用图或者式子表示出来？

（学生自主尝试后，展示交流）

生1：妈妈的收入×2+500=爸爸的收入。

生2：我是画线段图，如下图。

生 3：我是用天平图，天平一边表示妈妈的收入×2+500，另一边表示爸爸的收入。（图略）

生4：爸爸的收入÷2－500=妈妈的收入。

生5：我觉得生4的说法不对，从线段图上可以看出，妈妈的收入应该是（爸爸的收入-500）÷2。

（其他学生点头表示同意）

师：比较一下，我们会发现线段图能很清楚地反映出数量之间相等的关系，相比于式子，线段图——

生：直观。

师：说得好！那么，直观是什么意思呢？

生：直观就是可以“直接地看出来”。

评析：在表示等量关系的探索中，学生自主尝试，想出了用等式、线段图、天平图等多种方式进行数学表达。在不同的数学表达中，学生加深了对概念的理解，同时通过进一步的对比体验了线段图直观的价值。

五、数形结合，感悟“等量关系”

师：同学们，请注意观察，你能发现其中的等量关系吗？

（课件动态演示：两条长度相等的线段，一条围成长方形，一条围成正方形。如下图）

生：围成长方形线段的长度=围成正方形线段的长度。

生：长方形的周长=正方形的周长。

生：（长+宽）×2=长方形的周长。

生：边长×4=正方形的周长。

生：（长+宽）×2=边长×4。

师：仔细观察下图，你能找出题中的等量关系吗？能找出几个？试着在本子上写一写。

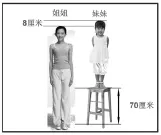
（学生自主完成后汇报）

生：姐姐的身高+8=妹妹的身高+椅子的高度。

生：姐姐的身高-70=妹妹的身高-8。

评析：史宁中教授认为：方程的本质是“在讲两个故事，这两个故事在数量上相等”。等量关系的数学本质正在于此。本环节通过数形结合的例子让学生形象地感悟等量关系的本质含义，鼓励学生从不同的角度观察、分析、把握数量间的相等关系，提升学生思维的灵活性和深刻性。

六、走进生活，寻找“等量关系”

（1）广告中的等量关系。（略）

（2）生活中的等量关系。（略）

【总评】

一、数学概念的教学不是孤立的数学概念的教学

将数学概念“嵌入”数学背景与结构之中，让学生感受所学的概念位于数学背景中的“哪个位置”，“镶嵌”在数学结构中的“哪个地方”，这对于学生建立完整的知识系统是极其重要的。

就本课而言，等量关系的教学按照以下的逻辑顺序展开：等量关系是一种关系，是一种数量关系，是数量上的一种相等关系。这样的顺序与线索巧妙地将等量关系“镶嵌”在数量关系中，让学生对等量关系的理解建立在对数量关系的把握上，这对于学生形成结构化的知识网络是很有帮助的。

二、数学概念的教学是概念数学本质的教学

数学概念的教学是概念数学本质的教学，这有两重含义：其一，重点在于引导学生理解数学概念的数学本质；其二，活动的目标应当指向对数学概念的理解。在本课的教学中，教师通过制造冲突的问题情境，让学生感知了等量关系就是数量间相等的关系，进而让学生在数学问题中寻找等量关系，用不同方式表达对等量关系的理解，而后借助数形结合，让学生感悟等量关系的本质是“在讲两个故事，这两个故事在数量上相等”，让学生对等量关系有更进一步的体悟与理解。

在整个学习过程中，教师始终围绕“等量关系的数学本质”展开教学，在学习过程中涉及“怎么找等量关系”“怎么表示等量关系”等学习内容，这些学习内容表面上看似是技能目标的学习，实际上是借助寻找、表达等活动深化对概念本质意义的理解。显然，只有聚焦目标才能实现目标。

三、数学概念的建立是个体自主建构的过程

数学概念的建立离不开数学活动的经历。纵观本课的教学过程，教师从“无法解答的数学问题”入手，让学生分析其原因，以此引入数量关系；接着，教师设计了在“天平图”上创造等量关系的数学活动，让学生在创造中初步感知等量关系的意义；而后通过寻找等量关系、表示等量关系等一系列数学活动，促进学生理解等量关系的数学本质，从而完成数学概念的建构过程。

教师借助巧妙的数学活动，将学生对等量关系的学习，顺应到数量关系这一上位的数学概念之中，这一顺应的过程使学生对数学概念的理解与建构达到了结构化的水平。这对于概念的理解、巩固与应用是很有意义的。

（作者单位：福建厦门市华昌小学，福建惠安县山霞中心小学）