追寻历史足迹,让启发自然
——以“圆的面积”一课为例
2016-06-28仲爱云
◇仲爱云
追寻历史足迹,让启发自然
——以“圆的面积”一课为例
◇仲爱云
一 问题的提出:启发在哪里?
听罢实习生执教的“圆的面积”一课,教学过程顺畅,可又感觉生硬、别扭;教学环节丝丝入扣,可又觉得少了许多。我想说老师提问太多,没有留给学生任何机会,实习生说是为了“启发”。究竟启发在哪里呢?不妨回顾教学过程中的几个片段。
片段一:揭示课题,初步估算
(教师把圆形图片置于方格纸内,如图1)

图1
师:怎样数?
生:不足1格按半格算。
师:如果非常接近1格时,怎么办?
生:可以按1格算。
师:这么大的圆形,都要数吗?
生:是的。
师:有更简单的方法吗?
生1:只要数出其中的四分之一。
生2:只要数出那个小正方形中的空白处,就可以求出它的四分之一了。
片段二:进一步验证
过渡语:圆的面积大约是其半径平方的3倍多一点,但具体是多少我们还不太清楚,我们需要更加精确的数据来表示。
师:请同学们回忆一下,在求平行四边形、三角形、梯形等图形的面积时,我们是用什么方法进行推导的?
(生答,略)
师:那我们能否用剪拼的转化方法推导出圆的面积呢?请大家讨论一下。
(生讨论)
师:怎么剪呀?
生:可以沿半径剪,也可以沿直径剪。
师:假设把它剪成了4等份,怎么拼呢?
(师在课件上示范剪成8等份时剪、拼的转化方法。以16等份为例,让学生小组合作拼,拼成一个近似的平行四边形)
师:像长方形吗?近似长方形的长与圆有什么关系呢?近似长方形的宽呢?长方形的面积你能求出来吗?在转化的过程中,圆的面积变了吗?那此时你能得出圆的面积应该怎么求吗?
(生一一回答,略)
启发,源于孔子的“不愤不启,不悱不发”。百度百科释义为:开导指点或阐明事例,引起对方联想并有所领悟。启发式教学,主要就是教会学生质疑,积极思考。看片段一和片段二,师问生答,教学过程顺畅,学生没有“疑”,没有自我“思”,当然也没有“悟”,启发在哪里呢?没有波澜起伏,更缺少教学深度。随着课程改革的推进,课堂摒弃了满堂灌,启发式教学成为人们的共识。但是满堂问替代了满堂灌,而满堂问并不意味着就是启发,只是冠名“启发”,实为“代发”。
二 诊断问题:如何变“代发”为“启发”?
1.启发需要等待:从曹冲称象的故事说起。
在猜想圆面积公式前,老师由曹冲称象的故事引出了“转化”的思想。
讲故事的目的是什么?显然是为了启发学生获取推导圆面积公式的思路。既然如此,就应该留出时间供学生思考。无论学生是否有思路,都必须耐心等,给学生机会,不怕没有惊喜,就怕老师缺少发现。在课堂上,有这么一个环节:
生1:老师,我有办法了——称。
(大家都纳闷:面积也能称?)
生1:(继续)可以用沙子铺成一个圆(一层),然后再铺一个边长等于直径的正方形。面积的比就是它们对应沙子的质量的比。
可惜,老师以沉默和不搭理“攻击”了学生。
探寻圆面积推导的历史足迹:
有一天,卡瓦利里的目光落在自己的衣服上时,他忽然灵机一动:咦,布不是可以看成面积吗?布是由棉线织成的,要是把布拆开的话,拆到棉线就为止了。我们要是把面积像布一样拆开,拆到哪儿为止呢?应该拆到线段为止……几何学规定平面是没有厚薄的,这样也是有道理的。卡瓦利里紧紧抓住自己的想法,反复琢磨,提出了求圆面积的新方法。
沙子间也许还有缝隙,学生的思考不会达到卡瓦利里那么缜密、那么深入,不过有几分历史相似性。老师不妨说,沙子未必铺得均匀,可以把沙子换成布。沿着历史的足迹,学生在这样的历史文化氛围中,受到鼓舞,更容易产生猜想。充分利用学生把圆放在正方形内,利用“化圆为方”的雏形,因势利导,形成启发。学生的回答也许不是老师心中所想的,也不是老师所预料到的,课堂教学显得不那么“风平浪静”,可这样正是真实、自然的,耐心等待,让学生充分思考后,启发才有用武之地。
2.启发要有主旨:从曹冲称象到数方格。
也许很多老师会说:不是面对每个班级,讲完曹冲称象的故事,等待后都有学生回答;即使学生的回答“百花齐放”,但往往偏离正题很远。
学生听了故事而没有回答,说明故事本身未能引起学生足够的兴趣。曹冲称象是个好故事,但对于六年级的学生,已耳熟能详了,这可能导致启而一言不“发”。如果学生很配合老师,但回答“跑题”,那我们就不得不反思:故事本身“启点”在哪里?曹冲称象的“转化”能撬开我们圆面积公式推导的思路吗?学生的表现说明“启点”不够突出,不足以让学生产生类比或联想。我们进一步看教学片段,发现故事与数方格衔接不紧密,与后面的验证猜想、推导公式中的数学思想“铆合”不紧密。因此,这个故事不太容易让大多数学生形成有效的启发,可谓远水解不了近渴。
片段三:
师:很好。下面请大家根据这些方法,打开书本,数一数、算一算每个图形的面积有多大。第一组数图2,第二组数图3,第三组数图4。
师:数的过程中可能会产生一些误差,只要结果在这个范围内,就算正确,并从中选出任意一个数据进行研究,看看圆的面积与半径有什么关系。

图2:49~51cm2 图3:29~31cm2 图4:77~79cm2
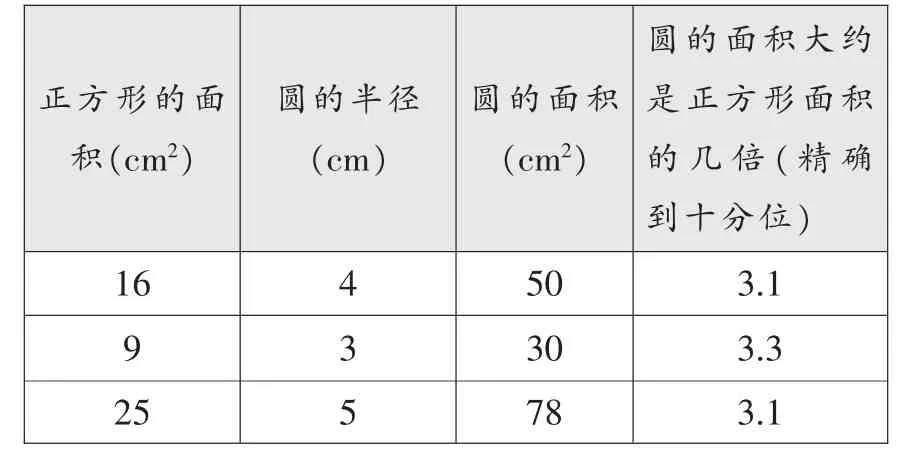
正方形的面积(cm2)圆的半径(cm)圆的面积(cm2)圆的面积大约是正方形面积的几倍(精确到十分位)164503.1 9 3 303.3 255783.1
老师给出了三个面积不等的圆,让学生由三组数据找出规律,猜想出圆的面积与半径的关系。这一步做得不错,但差一点火候,学生的思维完全可以进一步发展。我们不妨把方格细分,边长由1cm到1mm,会得出表格中第四列的数据(精确到百分位)约为3.14;再进一步细分,利用计算机演示,步步细分,逐步逼近……在由粗略到逐步精确的过程中,学生能更自然地猜想出圆面积与半径平方的关系和圆周率有关。
考察圆面积公式的历史足迹:
在古希腊,求圆面积问题是当时三大数学难题之一。公元前5世纪,哲学家阿拉克萨克放弃财产,研究圆面积。辩士、诗人安提丰首次提出用圆内接正多边形解决圆面积问题的设想,但要得出公式还是空中楼阁。阿基米德、卡瓦利里、开普勒以及中国的刘徽等是在前人的基础上突破了“从有限到无限”,实现了“以直代曲”,用不同的方法提出了圆面积公式。
历史是一面镜子,它启示我们:渗透以直代曲、极限的数学思想是启发的重点与难点。在小学中,我们当然不会去讲以直代曲和极限,但我们可以带领学生往这个方向去想。正如安提丰一样,哪怕是先设想一个空中楼阁也行。进一步,数方格至少可以让学生在从近似往精确的路上往前迈一步。这样数方格就不是止于“数”,而是启发学生有了思考。接着,将圆与方格的一个个交点顺次连接,学生感悟:方格越细小,越精确,圆内接多边形的面积越接近圆的面积。学生自然有了疑虑:再怎么精确,总还是近似,该怎么办?
概念的形成是个缓慢的内化过程,具有“不可见”性,启发的方向尤为重要。我们要用长远的眼光来对待教学,不能只为了表面上“得出”公式。对小学生不能讲以直代曲,不能讲极限,但这节课承载着渗透以直代曲、极限思想的使命,最起码要让小学生知道“随着方格越来越细小,圆内接多边形的面积越来越接近圆的面积”。
3.启发应拒绝“过度分析”。
《学会生存》一书曾做出论述:“教师的职责在于越来越少地传授知识,越来越多地激励思考,除他的正式职能外,他越来越成为一位顾问,一位意见交换者,一位帮助发现矛盾论点而不是拿出现成真理的人。”
考察片段一和片段二,比如在数方格(片段一)的时候,就应放手让学生去数,信任学生,很少有学生那么傻,数多的或数全部。即便如此,有个别学生数的方法不够好,通过小组合作观察别人的方法,自己也能够“纠正”,这正好可提高学生自身的“免疫能力”。片段二中,老师详细分析如何剪、如何拼,牵着学生把圆剪拼成长方形。过度的分析等于扼杀了学生丰富的想象力。因为圆的面积公式的推导不是靠直观经验就能获得的,它必须借助想象和理性思维。太着眼于细节和局部的分析,学生就会失去独立思维与判断的机会,反而起不到启发的效果。
对比改进:
预先让学生用一张正方形的纸和一把剪刀(不用圆规)剪出一个“圆”,看谁剪得够圆。让学生充分交流后,问学生发现了什么。
生:有的同学剪得很圆,有的剪得不怎么圆。
师:为什么?
生:折得越多越接近圆。
生:折得越多,圆的每个小扇形就越接近三角形。
生:只要折得够多(分得越多,直至无穷多)圆的面积就可以转化分割成很多小三角形的面积。
……
然后,让学生交流,讨论如何求这些小三角形面积的和。可以剪拼成三角形、梯形、长方形,让学生自己去决定拼成什么图形,培养他们独立思考、做出判断的能力。
接着,可以向学生介绍17世纪开普勒在结婚时,思考葡萄酒桶体积算法时想出圆面积计算方法的小故事。不去拼,而是把“小三角形”转化成等底等高的三角形。(如图5)

图5
4.启发要从大处着眼、小处着手。
启发拒绝过度分析,要有自由度与开放度,但不是不注重细节,放手不是放任和随意。正因为从大处着眼了,启发有了主旨,每个环节、每个细节都要为之服务,甚至每句话都得仔细推敲。例如在片段三中,“师:在数的过程中会产生一些误差,只要结果在这个范围内,就算正确,并从中选出任意一个数据进行研究。”数的过程中怎么会产生误差?数就不应该有误差。如果不准确,不是数的原因。“只要结果在这个范围内,就算正确”,既然老师都算正确,学生哪有动力去追求更精确或者准确的呢?这不是和“从近似走向准确”矛盾吗?这也使得学生缺少了去思维的动机。看来老师“少讲,少些言语”不一定不是启发,你不说,学生还有疑问呢!正好留给学生思考的机会,再怎么数,再怎么细化方格,只要是有限次的,总还是近似的,不是准确的。看来启发的语言要推敲,甚至语气等都别有一番讲究。讲得多,问得多,甚至满堂问未必就是启发,不是有问题就是启发,要看怎么问,由谁来问。启发有技巧,每个细节都必须关注,真所谓“细节决定成败”。
[1]弗赖登塔尔.作为教育任务的数学[M].上海:上海教育出版社,1999.
[2]高燕,胡媛.圆的面积:从历史到课堂[J].上海中学数学,2014,(5):1—3.
(作者单位:江苏南通师范高等专科学校如皋校区)
