在问题提出中拓展数学的理解——以“100以内数的整理与复习”一课为例

执教/杨薪意 评析/蔡金法

在问题提出中拓展数学的理解
——以“100以内数的整理与复习”一课为例

执教/杨薪意 评析/蔡金法

随着课堂教学的不断改进，在课堂教学中，利用问题提出促进学生对相关概念的数学学习与数学理解越来越被老师认可和接受。于是，在课堂教学中，教师应该如何以问题提出为核心，通过问题提出来帮助学生理解数学就成为学术界和一线教师共同探讨的话题。在本文中，我们将以一节小学一年级 “100以内数的整理与复习”为例，来探讨在第一学段如何帮助学生在问题提出中拓展对数学的理解，成为更好的问题提出者。

镜头一:交流同一个数的多种表达方式

师：上课前，请同学们先悄悄地在卡片上任意写一个今天你喜欢的两位数，不要告诉其他同学哦。

【设计意图：以神秘的活动开课，既能沟通师生关系，更能激发学生的学习兴趣，诱发学生的好奇心，让学生对新课充满期待，自主地为投入新课的学习做好充分的精神准备。】

师：谁愿意用数学的表达方式，让大家猜一猜你喜欢的数是几？

【设计意图：通过“猜一猜”，引发学生主动思考 “如何用数学的表达方式描述自己的这个数”。以此帮助学生自主回顾、梳理对100以内数的认识，并在全班互动交流中达到多角度认识数的组成，感受理解同一个数表达方法的多样化，培养数感的目的。】

生1：我喜欢的数比40少1。你们知道我喜欢的数是几吗？

生2：你喜欢的数是39。

生1：恭喜你答对了。请说说你喜欢的数吧。

（师板书39）

生2：我喜欢的数在26和28中间。

生3：你喜欢的数是27。

生2：恭喜你答对了。

（师板书27）

师追问：这个数还可以怎么表达？

生4：比30少3的数是27。

生5：比25多2的数是27。

生6：比20多7的数是27。

生7：比100少73的数是27。

生8：2个十和7个一组成的数是27。

生9：7个一和2个十组成的数是27。

生10：摆2捆小棒和7根小棒就是27。

生11：在计数器上，个位上拨2个珠子，十位上拨7个珠子就是27。

生12：不对。应该是在十位上拨2个珠子，个位上拨7个珠子才是27。

生11：不好意思，我说错了。谢谢纠正。

生12：（生画图，如下）这样也是27。

图1

师追问：谁看懂生12的意思了？

生13：1颗大的爱心表示1个十，2颗表示2个十；1颗小的爱心表示1个一，7颗表示7个一。合起来就是27。

生14：十位上是2，个位上的数比十位上的数多5的数是27。

……

显然，在这个镜头中，我们看到教师把有关数的组成的内容全权下放，交给学生，在貌似“猜数”的游戏交流过程中，由学生自己采用个性化的方式，通过问题提出完成对一个数的描述和说理，并在生生互动中，进一步理解可以用多种方法表达同一个数。

镜头二：讨论数与数之间的关系

师：根据39、27这两个数，你能联想到哪些和它们相关的数？

【设计意图：通过“联想相关数”，拓展学生数感，理解位值制，认识同一个数字在不同的数位上表示不同的意义。】

生1：我联想到72和93。

师指导生1：很好！建议你最好再问问大家，有没有人知道你是怎么联想到的。

生1：同学们，你们知道我是怎么想到这两个数的吗？

生2：我想你是把27和39十位上的数字和个位上的数字交换位置得到的。

生1：很聪明！我就是这样想的。

师：像这样把一个数十位上的数字和个位上的数字交换位置得到的新数，和原来的数表示的意义一样吗？

生3：不一样。27的“2”在十位上，表示2个十；72中的“2”在个位上，表示2个一。

生4：72比27多得多，27比72少得多。

生5：我想到了比27大、比39小的数有：28、29、30、31、32、33、34、35、36、37、38。

生6：我又联想到了比27大、比39小的双数有：28、30、32、34、36、38。

生7：我还联想到了比27大、比39小的单数有：29、31、33、35、37。

生8：我想到27前面的数有26、25、24……

生9：我想到39后面的数是40。

生10：我想到66。你们知道我是怎么想到的吗？

生11：你是把27和39加起来得到的。

师：太好了！生10想到了这两个数的和。

（师板书“和”，并写出算式27＋39＝66）

生12：按生10的想法，我又联想到了它们的差是12。

（师板书“差”，并写出算式39－27＝12）

师追问：他们都算对了吗？你能想办法验证一下吗？

（鼓励学生用自己的算法验证）

【设计意图：通过检验同伴是不是算对了，帮助学生对算理进行自我梳理，一方面巩固自己喜欢的算法，另一方面理顺自己尚不熟悉的算法，体会算法的多样化，理解不同算法的思维路径，感受不同算法之间的联系。】

图2：学生检验27＋39＝66的不同算法

图3：学生检验39－27＝12的不同算法

通过镜头一和镜头二，我们感受到通过问题提出展开教学，学生能主动参与学习，对一个数能从不同的角度观察、解释，对两个数能从不同的角度建立联系、沟通关系，进而理解数与数之间的运算，体会“位值”的作用。

镜头三：提出加法问题

师：运用27＋39＝66这个加法算式，你能解决生活中的哪些问题？

【设计意图：借助将算式还原成生活原型的活动，引导学生回归生活，在提出不同的实际问题的过程中感受数学与生活的密切联系，体会加法、减法的数学意义。】

这个环节在实际教学时，不论是在城区学校还是在农村学校，学生的课堂表现都相当精彩。大部分学生都能围绕自己现实的学习环境、生活背景，提出各种鲜活而富有生活味儿的数学问题。

①红花有27朵，黄花有39朵，一共有多少朵花？

②上午挖了27个土豆，下午挖了39个土豆，一天挖了多少个土豆？

③树上有39只小鸟，又飞来27只小鸟，现在树上有多少只小鸟？

④笑笑拍了27下球，淘气比笑笑多拍39下，淘气拍了多少下？

⑤一盒饼干，我吃了27块，还有39块。饼干盒里原来有多少块饼干？

师质疑：问题①是求“一共有多少”，“一共”这个词很好理解，就是“把红花和黄花两个部分合起来”，（师手势配合）老师明白用加法计算。可是问题②、③、④、⑤里没有问“一共”，为什么你们也用加法计算呢？

师求助：谁能帮帮我，要怎么理解呢？

生1：问题②“一天挖了多少个土豆？”“一天”就是要把上午挖的和下午挖的合起来，（生模仿教师手势表示）所以，也是用加法。

生2：问题③“现在树上有多少只小鸟？”“现在”就是把原来的小鸟和又飞来的小鸟合起来，（生手势表示）所以，也是用加法。

生3：问题④虽然没有用“一共”，但是，因为淘气要比笑笑多拍39下，（生特别重读“多”）所以，就要在笑笑“27下”的基础上再加39下，才是淘气的。淘气很厉害。

师：你能结合这幅图解释一下吗？

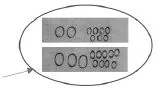
图4

生3：我还没想好。

生4：我可以帮他。上面的是笑笑拍的下数，下面的是淘气比笑笑多拍的下数，上面的和下面的合起来（边说边画集合圈）就是淘气拍的下数。

生5：问题⑤“原来”的意思就是没有吃之前的饼干数量。所以，要把吃了的和剩下的合起来，也是用加法。

在镜头三中，通过师生互动，学生达成共识：这些问题虽然问法不同，但是算理一样，都是要把两个部分的数合起来，求和，所以都可以用加法解决。

镜头四：提出减法问题

在完成对加法算式意义的整理后，用39－27＝12这个减法算式，又能帮助我们解决生活中的哪些问题？在教师的引领下，学生生成了以下这样的问题：

①停车场原来有39辆车，开走27辆车，还剩下多少辆？

②老师有39本书，发给学生27本，还剩下多少本？

③有 27张凳子，来了39个人，还差几张凳子？

④笑笑得了39颗星星，淘气得了27颗星星。笑笑比淘气多多少颗星星？

⑤笑笑收了27个废电池，淘气收了39个废电池，笑笑比淘气少收多少个？

⑥苹果有39个，菠萝比苹果少27个，菠萝有多少个？

⑦女生有39人，男生比女生少27人。男生有多少人？

⑧小白兔有39个萝卜，小灰兔有27个萝卜。小灰兔再拔几个就和小白兔的一样多了？

⑨大盒子里有39块积木，小盒子里有27块积木。大盒子里要拿走几块积木就和小盒子里的积木同样多了？

……

在镜头四中，我们看到学生通过问题提出，既能提出用减法解决部分数的生活问题（如问题①～②），也能提出用减法解决相差数的问题（如问题③～⑤，⑧～⑨），还能提出用减法解决比一个数多（或少）几的数是多少的逆问题（如问题⑥～⑦）。

在解释为什么能用减法解决这些问题时，学生也能用自己的语言、手势或画图来说明数量关系，最终达成共识：这些问题虽然场景不同，问法不同，但是算理是一样的，都是求相差数（或部分数）。因此，都可以用减法来解决。

如果说教育的目的是培养学生未来生活所需要的思考能力的话，通过本课例，我们可以看到用“问题提出”来帮助学生认识数，有助于学生数感的培养；用“问题提出”来帮助学生理解题意，有助于学生对加法、减法意义的理解。

评析

在过去的十几年中，我一直从事有关数学问题提出的研究，有足够的证据说明，中小学学生是有能力提出有意义且在数学上较为复杂的问题的。同时，一些小型研究表明，从事问题提出的活动，学生参与的思维活动更加活跃，并且学生能够根据自己的生活经验和学习经验提出问题。也有一些研究表明，从事问题提出的活动不仅能促使学生对数学学习产生美好的情感，更能促进学生问题解决能力的提高。既然问题提出的好处那么多，为什么我们不在课堂上多提供机会让学生参与从事数学问题提出的活动呢？

为此，我一直在探索如何在课堂上提供机会让学生参与问题提出活动。在大学授课时，我用问题提出教数学；在教师培训时，我用问题提出让教师思考、研究教学问题。同时，我留心收集有关问题提出的教学案例。在一个偶然的机会我知道了杨薪意老师的这节课，观课后很兴奋。这是一节典型的通过提出问题让学生学习数学的好课。

这节课的一大特点是新颖的设计。从猜数开始，学生在不知不觉的游戏中加深对数的特性的理解。此课的精彩之处在于让学生提出不同类型的加减法问题。与传统的通过“关键词”来帮助学生判断到底是加法问题还是减法问题相比，用“问题提出”的教学能帮助学生深刻体会“两个数为什么相加”“两个数为什么相减”，这样的教学更有实效。教育研究表明，用“关键词”来判断到底是加法问题还是减法问题的教学往往是基于死记硬背的，是不利于学生从数学本质上理解加减法意义的，也是有碍于学生用数学思维灵活解决问题的。在这节课中，杨老师的设计是“逆向”的，让学生根据课堂生成的算式设计现实问题，而这些问题还能用这个算式解答。在这个基础上，杨老师引导学生解释不同问题串的现实意义，帮助学生从数学层面理解并领会加减法意义，最后确定用加法还是减法解决问题。从认知的角度来说，这样的逆向思维是更高的思维层次。

这节课的第二大特点是其生成性。似乎一切活动都来自于学生。有的老师也许会担心，万一学生没有提到某类问题怎么办？确实，这样的教学是需要经验的。从我观课以及和杨老师的交流中，我感受到，只要注重两大关键，这样的教法所有老师都能掌握。第一是学习目标。这是一节复习课，尽管整节课的练习题都是当堂生成的，但一切都是围绕着学习目标进行的。第二是教师充分的准备。这节课杨老师是做了充分准备的，她预设了学生可能给出的问题。如果学生在课堂上没有提出某类比较重要的问题，杨老师会以参与交流的伙伴这一角色巧妙地提出来。

这节课的第三大特点是把提出问题作为教学手段来进行实施。也许有的老师会担心：学生没有太多问题提出的经验和训练，他们提不出问题怎么办？其实不用担心，学生提出问题的能力比我们想象的要高得多(Caietal.，2015)[1]。尽管这是一节复习课，但是，通过这节课，我知道在新授课时，杨老师同样也是用问题提出来帮助学生学数学，加深理解的。

本课例，从一个侧面告诉我们，课堂上问题提出的宽度和深度决定了学生数学学习的宽度和深度，进而决定了数学学习目标的达成情况。另外，教师也可以运用问题提出的任务帮助我们了解学生的数学理解水平。我们有理由相信，问题提出应成为学校课程的一个重要组成部分。教师不仅需要给学生提出问题创造条件，还需要帮助学生成为更好的问题提出者，为学生提供经历探究、猜想和提出问题的机会。希望杨老师的这个课例能给广大教师带来一点启发，希望在今后能看到更多的问题提出的精彩课例。

[1]CaiJ.， HwangS.， JiangC.， SilberS. (2015).Problem posing research in mathematics: Someansweredandunansweredquestions[M].InF. M.Singer，N.Ellerton，J.Cai（Eds.），Mathematical problem posing： From research to effective practice（p.3-34）.NewYork，NY：Springer.

（作者单位：四川成都市行知小学，美国特拉华大学）