QVIP的广义间隙函数和误差界

赵张超，胡艳红，徐延新

（哈尔滨师范大学数学科学学院，黑龙江哈尔滨150025）



QVIP的广义间隙函数和误差界

赵张超，胡艳红，徐延新

（哈尔滨师范大学数学科学学院，黑龙江哈尔滨150025）

摘 要：对拟变分不等式，定义广义间隙函数并研究其性质。通过使用广义间隙函数，在所研究拟变分不等式问题的目标函数关于解是强单调、Lipschitz连续的条件时，得到误差界。

关键词：拟变分不等式；间隙函数；误差界

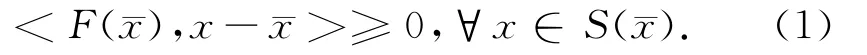
这里F：Rn→Rn是连续映射代表Rn中的内积。是集值映射，且S（x）是一个闭凸集，∀x∈Rn。当S是常值映射时，（QVIP）就退化成文献［1］中研究的（VIP）问题：

用H=｛x∈Rn|x∈S（x）｝表示（QVIP）的可行集。拟变分不等式问题在经济、社会和其他领域有着广泛的应用，经济问题中的广义均衡问题可以等价地转换成拟变分不等式问题，可见文献［2］。利用间隙函数是目前研究变分不等式问题较常用的方法，但拟变分不等式问题由于其自身的复杂性，这方面的结果并不多见。

2007年，Fukushima在文献［3］中作为VIP间给出了QVIP的间隙函数。2008年，Taji在文献［4］中，推广了文献［3］的结果，他利用满足某些条件的φ（x，y）给出了QVIP的广义正则间隙函数和D-间隙函数，但遗憾的是文献［3-4］都没有给出误差界结果。2012年，Rachana Guptha等在文献［5］中继续研究了拟变分不等式的间隙函数和误差界，但是他们在建立间隙函数时使用的仍然是隙函数的直接推广，利用

受到文献［3-5］的启发，利用φ（x，y）给出了QVIP的广义正则间隙函数和D-间隙函数，并且得到了全局误差界结果。

1　预备知识

首先回忆一些相关知识。

定义2.1 映射F：Rn→Rn在Rn上强单调，模μ＞0，是指

定义2.2 映射F：Rn→Rn在Rn上Lipschitz连续，模L＞0，是指〈F（x）-F（y），x-y〉≤L‖x-y‖，∀x，y∈Rn.

本文要求函数φ：Rn×Rn→Rn满足：

1）φ在Rn×Rn上连续可微；

2）φ在Rn×Rn上非负；

3）φ（x，·）关于x是一致强凸的：存在常数λ＞0，∀x∈Rn，满足

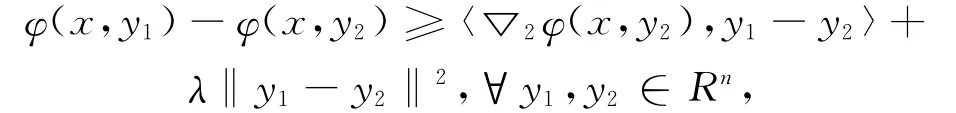
这里▽2φ是函数φ关于第二个变量的偏导。

4）φ（x，y）=0当且仅当x=y；

5）▽2φ（x，·）是一致Lipshcitz连续的，即∃L′＞0，使得∀x∈Rn有

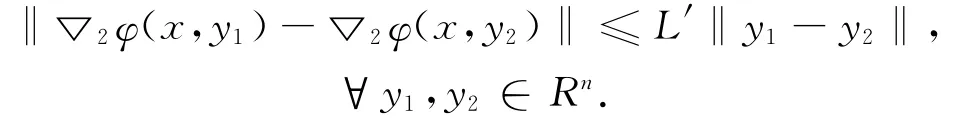
引理2.1［6］设函数φ满足条件1）～4），那么▽2φ（x，y）=0当且仅当x=y，∀x，y∈Rn。

引理2.2［7］设函数φ满足条件3），那么∀y1，y2∈Rn，有

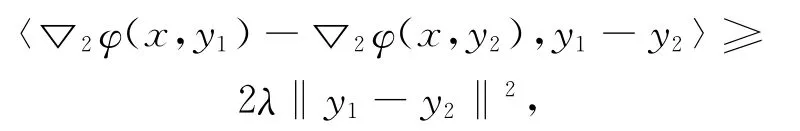
即▽2φ（x，·）在Rn上是强单调的，模2λ，这里λ是3）中给定的。

引理2.3［8］设函数φ满足条件1）～5），λ，L′是相对应的系数，那么

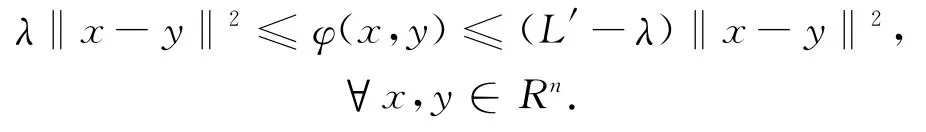
2　QVIP的广义间隙函数和误差界

由于φ（x，·）是一致强凸的，-ψα（x，·）在S（x）上也是一致强凸的，因而在S（x）上存在唯一最小点πα（x）。进而Gα（x）也可以表示为

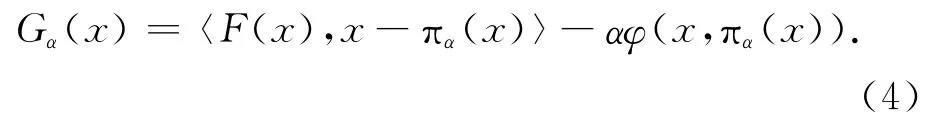
这里，给出一个重要引理，它刻画了QVIP解的充分必要条件。

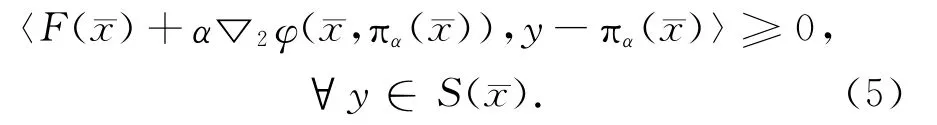
本节研究拟变分不等式（1）。首先，∀x∈Rn，定义广义正则间隙函数如下：若，则有，所以是QVIP的解。

引理3.2 设函数φ满足条件1）～4），那么，如下事实成立

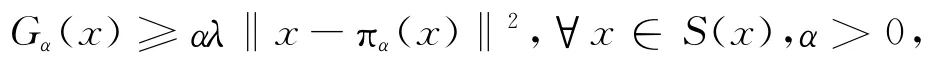
证明：∀x∈S（x），由式（4）知Gα（x）=〈F（x），x-πα（x）〉-αφ（x，πα（x）），由πα（x）是-ψα（x，·）在S（x）上的最小点，有〈F（x）+α▽2φ（x，πα（x）），y-πα（x）〉≥0，∀y∈S（x），

取y=x，则有〈F（x）+α▽2φ（x，πα（x）），xπα（x）〉≥0，

即〈F（x），x-πα（x）〉≥-α〈▽2φ（x，πα（x）），x-πα（x）〉，∀y∈S（x），

所以

后两个不等式分别由条件3）、4）得来。由引理3.1第二个结论显然成立。

下面的定理给出了自然剩余x-πα（x）提供全局误差界的条件。

定理3.1 设函数φ满足条件1）～4），假定

②∃k＞0，使得‖πα（x）-πα（y）‖≤k‖x-y‖，∀x，y∈Rn。

证明：由πα（x）是-ψα（x，·）在S（x）上的最小点，

有〈F（x）+α▽2φ（x，πα（x）），y-πα（x）〉≥0，∀y∈S（x），

由引理2.1可变形为〈F（x），x-πα（x）〉≥α

现在，给出Gα为QVIP提供全局误差界的条件。

定理3.2 设函数φ满足条件1）～4），假定

②∃k＞0，使得‖πα（x）-πα（y）‖≤k‖x-y‖，∀x，y∈Rn。

③∃M＞0，使得‖F（x）‖≤M，∀x∈H，

证明：首先由引理3.2知Gα（x）≥αλ‖xπα（x）‖2，∀x∈H。而定理3.1说明

现在，考虑QVIP的广义D-间隙函数。定义如下：

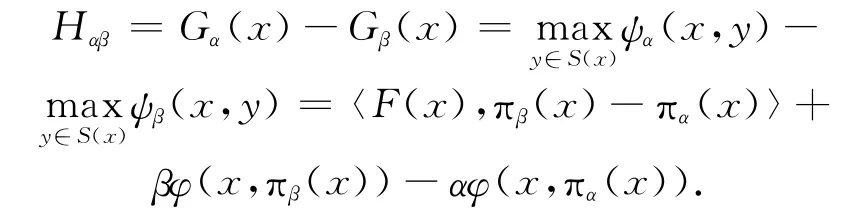
这里β＞α＞0，πα（x）和πβ（x）分别代表-ψα（x，·）和-ψβ（x，·）在S（x）上的唯一最小点。

接下来证明广义D-间隙函数在可行集上是非负的，并且它的零解就是QVIP的解。

命题3.1 设函数φ满足条件3），那么有

证明：

同样的方法可得不等式的另外一部分。

命题3.2 设函数φ满足条件1）～4），那么Hαβ在H上是非负的，特别地，当Hαβ=0时，x是QVIP的解。

证明：由命题3.1知，

由条件2）立刻知Hαβ在H上是非负的。接下来证明第二个结论。

假定Hαβ=0，那么由式（6），条件2）和4）可知x=πβ（x）。因此，由引理3.1知x=πα（x），由条件4）可得，φ（x，πα（x））=0，由Hαβ在H上是非负的，再根据命题3.1就有Hαβ=0。

基于上述结论，通过广义D-间隙函数来建立QVIP的全局误差界。

定理3.3 设函数φ满足条件1）～4），假定

②∃k＞0，使得‖πα（x）-πα（y）‖≤k‖x-y‖，∀x，y∈Rn。

③∃M＞0，使得‖F（x）‖≤M，∀x∈H，

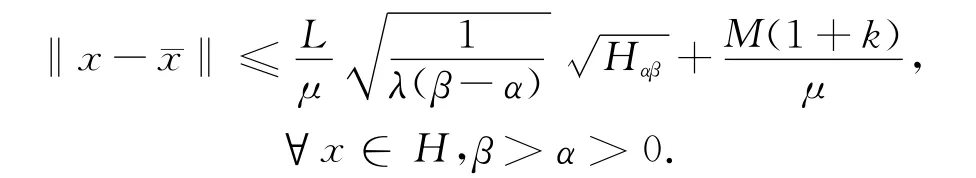
证明：由命题3.1，引理2.3和定理3.1，有

参考文献

［1］ FACCHINEI F，PANG J S.Finite dimensional variational inequalities and complementary problems［M］. Vol.I，Springer Series in Operations Research，Apringer，New york，NY，USA，2003.

［2］ HARKER P T.Generalized nash games and quasi-variational inequalities［J］.European Journal of Operational Research，1991，54（1）：81-94.

［3］ FUKUSHIMA M.A class of gap functions for quasivariational inequality problems［J］.Journal of industrial and Management Optimization，2007，3（2）：165-171.

［4］ KOUICHI Taji.On gap functions for quasi-variational inequalities［M］.Hindawi Pubblishing Corporation Abstract and Applies Analysis，2008，Art：ID531361，7PP.

［5］ GUPTA R，MEHRA A.Gap functions and error bounds for quasi-variational inequalities［J］.J Glob Optim，2012，53：737-748.

［6］ YAMASHITA N，TAJI K，FUKUSHIMA M.Unconstrained optimazation reformulations of variational inequality problems［J］.Journal of Optimization Theory and Applications，1997，92：439-456.

［7］ QU B，WANG C Y，ZHANG J Z.Convergence and error bound of a method for solving variational inequality problems via the generalized D-Gap function［J］.Journal of Optimization Theory and Applications，2003，119：535-552.

［8］ HUANG L R，NG K F.Equivalent optimization formulations and error bounds for variational inequality problem［J］.Journal of Optimization Theory and Applications，2005，125：299-314.

［责任编辑：郝丽英］

Generalized gap functions and error bounds for quasi variational inequalities

ZHAO Zhangchao，HU Yanhong，XU Yanxin
（School of Mathematical Science，Harbin Normal University，Harbin 150025，China）

Abstract：In this paper，it presents the generalized gap functions for quasi variational inequality and studies their properties.The error bounds are obtained when objective function for quasi variational inequality problem is strongly monotones and Lipschitz continuous on solution of quasi variational inequality problem.

Key words：quasi variational inequality；gap function；error bound

中图分类号：O174

文献标识码：A

文章编号：1671-4679（2016）02-0046-03

收稿日期：2015-12-31

基金项目：黑龙江省教育厅资助项目（12521147）；哈师大青年学术骨干资助计划项目（KGB201004）；黑龙江省自然科学基金资助项目（A201410）

作者简介：赵张超（1985-），男，硕士研究生，研究方向：最优化理论.