基于Matlab的七参数坐标转换研究与实现

李志伟，李克昭，2，赵磊杰

（1.河南理工大学测绘与国土信息工程学院，河南焦作454000；2.北斗导航应用技术协同创新中心，河南郑州450052）



基于Matlab的七参数坐标转换研究与实现

李志伟1，李克昭1，2，赵磊杰1

（1.河南理工大学测绘与国土信息工程学院，河南焦作454000；2.北斗导航应用技术协同创新中心，河南郑州450052）

摘 要：工程测量中，为了降低投影带来的变形过大问题，一般选择建立自己的独立坐标系统，不同坐标系之间的坐标转换成为迫切需要解决的问题。利用Matlab7.0软件中线性最小二乘拟合函数求取布尔莎坐标转换模型中的七参数，通过设计软件计算得到转换后的坐标和若干点间距离，并与相似模拟实验中钢尺测量的实际距离进行比较，得出基于布尔莎七参数坐标转换满足实际工程应用要求。

关键词：坐标转换；Matlab7.0；布尔莎七参数；相似模拟实验

目前，我国有1954北京坐标系、新1954北京坐标系、1980年国家大地坐标系、2000中国大地坐标系及GPS系统采用的WGS-84坐标系，还有一些地区由于工程建设的急需（如矿山开发、新城市建设等）而建立的局部独立坐标系等［1-2］。由于多种坐标系统的存在，在保存测量成果的过程中占用内存较大，资料管理混乱。为保证测量成果统一和使用方便，必须进行相应的坐标转换。参考文献［3-4］利用最小二乘原理实现二维平面坐标之间的转换；参考文献［5-6］从理论上分析了高精度空间直角坐标系之间的转换问题，并通过数学计算实现控制点之间的转换坐标。但对于工程测量而言，需要一种快速、简单并方便实现各种坐标系统之间的转换，同时要求转换结果准确、精度高的坐标转换模型。

坐标转换是一个复杂的数值计算过程，如果采用人工计算，不仅费时费力而且不能保证计算的精度。Matlab7.0软件为矩阵计算提供了平台，方便各种坐标转换模型的实现。文中选择理论上最成熟的布尔莎七参数坐标转换模型［7-10］，利用Matlab7.0软件中线性最小二乘拟合函数求取布尔莎坐标转换模型中的七参数，并通过设计软件计算得到转换后的坐标和若干点间距离，同时与设计的相似模拟实验中钢尺测量的实际距离进行比较。

1　布尔莎七参数坐标转换模型

布尔莎七参数模型又被称为七参数转换模型（7-Parameter Transformation），设有两三维空间直角坐标系OC-xCyCzC和OS-xSySzS，如图1所示。

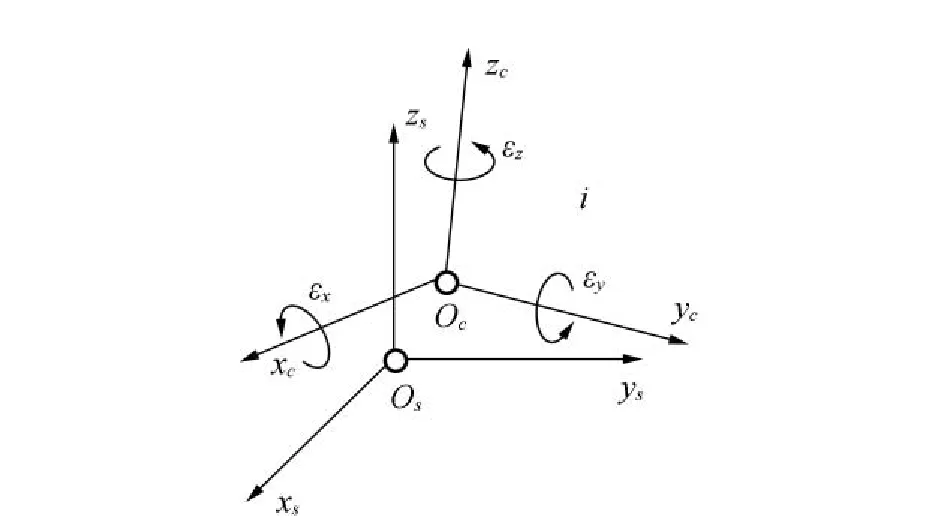
图1　两空间直角坐标系关系

由图1知，任意点i在两坐标系中的坐标之间有如下关系

转换参数的确定：以地心坐标系GNSS测量坐标转换成其他参心坐标系坐标为例进行七参数求解过程的论述。由式（1）知，如果参心坐标系至地心坐标系间的转换参数精确已知，则可将参心坐标系的坐标转换为地心坐标系的坐标；反之，亦可由地心坐标系的坐标求得参心坐标系的坐标。因此，上述转换模型在进行坐标相互转换的过程中具有至关重要的作用。在实际工作中，通常面对的问题是需要将GNSS观测、初算成果转换到当地的国家或地方独立坐标系中。若本地区没有相关的坐标转换参数，就涉及到坐标转换参数的确定问题。设地面网参心坐标系为OC-xCyCzC，地面网单独平差的点i的坐标向量中的坐标卫星测量的地面网的地心坐标系为OS-xSySzS，GNSS网单独平差的点i的坐标向量其中i=1，2，3，…。将和代入转换模型反求两个坐标系间的转换参数，然后利用所求得的转换参数再回代到模型中对GNSS测量的其它点进行坐标转换。将式（1）的布尔莎转换模型写成如下形式

式中：xiS，yiS，ziS为点i在坐标系OS-xSySzS中的坐标。

式（2）也可表示为

要确定7个参数，至少需要同时知道3个公共点在两坐标系的坐标值，利用最小二乘法对参数USC进行求解。由于这两个坐标系分别属于卫星网的地心坐标系（S）和地面网的参心坐标系（C），所以将这个求解过程称为卫星网与地面网的联合平差。

将式（5）代入式（4），得

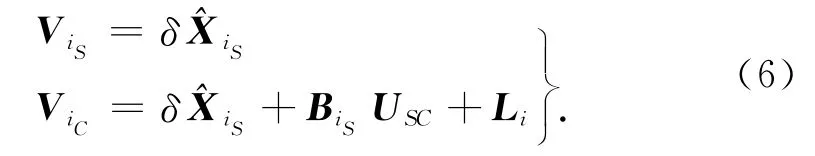
将式（6）写成一般形式为

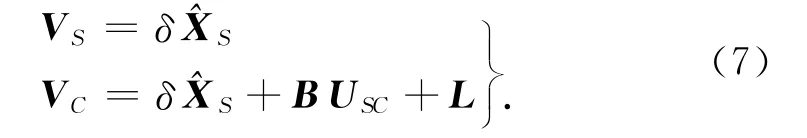
由此组成法方程式

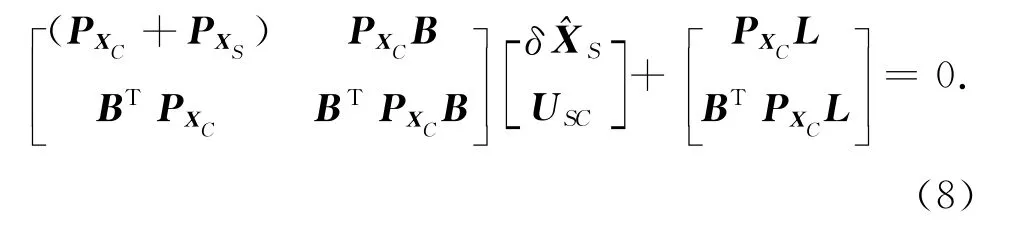
可求得其解为

2　相似理论模拟实验

模型模拟试验是现代科学研究的一种有效的研究方法，相似理论模拟实验是模型模拟试验的基础。本文运用相似第一理论对坐标转换的成果进行评定。

2.1几何相似

几何相似模拟实验要求模型与原型相似，必须将原型尺寸，包括长度、宽度、高度等都按一定比例缩小（或放大）做成模型，即

式中：ai为长度相似常数，也称为模型比例尺；LM为模型的长度；LH为原型的长度。一般来说，模型比例尺越大越能反映原型的实际情况，但由于各方面的条件限制，模型不能做得太大。

2.2模型架的选择

根据模型的比例尺和研究目的，结合工程实际，为了方便全站仪观测以及钢尺能够精确量测点与点之间的距离，模型中布设测点的观测标志是大头针，观测时瞄准大头针的尾部中心位置。测点点号设置如下：全站仪观测控制点布设在模型架两侧的钢架上，每边布设2个控制点，左边钢架两控制点从上至下编号为C，D，右边钢架两控制点从上至下编号为F，E。布设控制点时应注意：4个控制点应完全框住控制区域，而且点C和点F应该利用全站仪使其严格控制在一条水平线上；同样，点D和点E也是如此。同时，还应保证点C和点D严格控制在一条竖直线上，点E和点F亦是如此。这样的设置在使用全站仪进行监测时是必要的，有助于观测结果的计算。测点编号按照行列式的编排方式，第一行第一列的测点编号为1-1，第一行第二列的编号为1-2，第一行第三列的编号为1-3，以此类推。布设测点的模型如图2所示，点C，D，E，F分别设在模型架左右两侧的固定架上，这些点相当于控制点。在地面的点A安设全站仪，以点C垂直于模型的平面为基准平面来观测点C，D，E，F的水平角和垂直角，并精密测量出点C，D，E，F之间的距离。其方法是在C-D（C-F、D-E、E-F）边上拉一钢尺用全站仪的横丝（或竖丝）瞄准点C（D，E，F），然后进行水平微调读取钢尺读数，以同样的方法读取点D的读数，点C，D的读数差即为C-D边的长度。用同样的方法量测其他各边，这些数据作为观测任一点的起算数据。当建筑场地的施工控制网为矩形格网时，设计的建筑物轴线往往与控制网相平行或垂直，采用直角坐标法测设建筑物的轴线点位比较方便。

图2　模型架

3　实验数据分析

选用点C，D，E，F4个公共控制点进行布尔莎七参数转换模型中七参数求解，C，D，E，F4个公共控制点坐标如表1所示。

通过Matlab7.0编写的程序利用C，D，E，F 4个公共控制点进行布尔莎七参数转换模型中七参数求解，得到的布尔莎七参数如表2所示。

通过Matlab7.0软件，编程实现布尔莎七参数坐标转换模型，并进行相应的坐标转换。从转换后的坐标中挑选12个有代表性的测点，将计算得到的两点之间距离与钢尺实际测量数据进行比较分析，结果如表3所示。

表1　控制点坐标

表2　布尔莎七参数

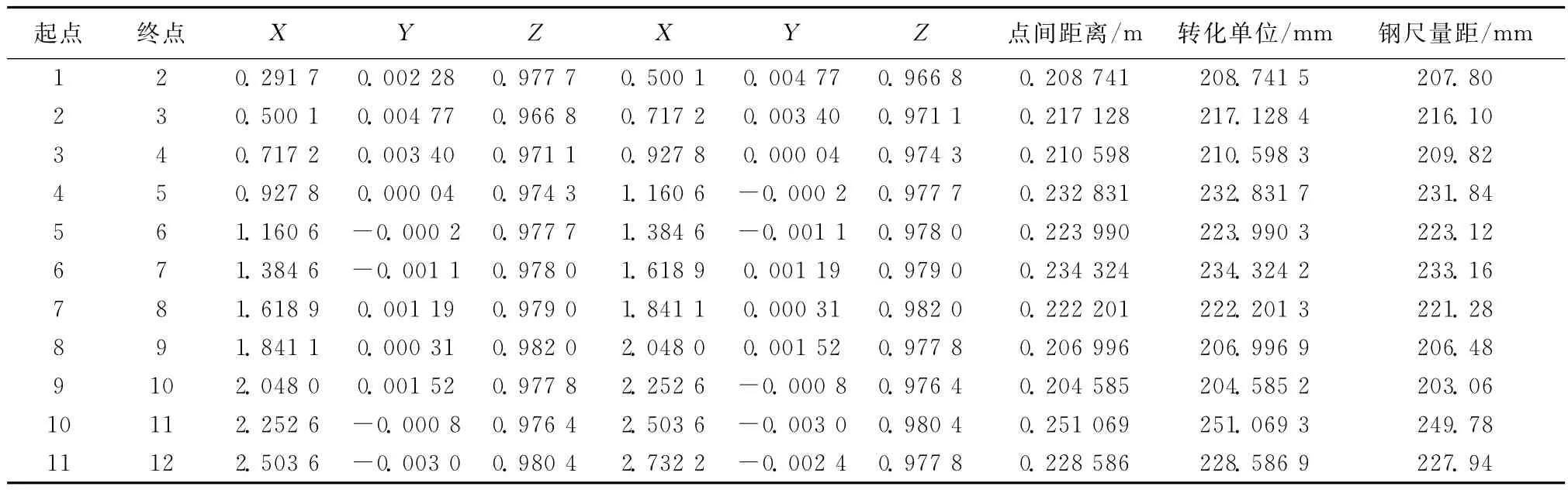
表3　坐标转换结果和实际量测距离对比

从表3得到的结果可以看出，由布尔莎七参数转换模型转换得到的坐标点之间的距离与钢尺实际量测的距离的差值满足工程测量限差的要求。因此，布尔莎七参数转换模型在空间直角坐标转换模型中是可行的。间接地证明了在不同坐标系统中进行坐标转换，布尔莎七参数模型是一种行之有效的方法。在工程测量中，拥有布尔莎七参数坐标转换模型的程序，在具有较高转换精度的前提下，可以快速解算工程所需要的独立坐标系的坐标，满足施工过程中的需求。

4　结束语

随着GNSS技术的不断发展和应用，全球定位信息需要结合转换技术和电子地图来完成，采用适当的坐标转换算法可以有效地提高我国监控和导航系统定位的精度。本文实现了任意坐标系与局部坐标系的空间直角坐标之间相互转换，采用最小二乘法计算布尔莎七参数转换模型的参数，编程实现了不同坐标系之间的坐标转换，所得到的转换结果满足工程测量的精度要求，对于工程测量过程中出现的新的坐标转换方法和数学模型都可以及时地更新到该坐标转换系统中。

参考文献

［1］ 周朝宪，董少波，和志军，等.自定义坐标系的建立及其坐标转换实现［J］.地质与勘探，2015，51（4）：699-704.

［2］ 韦钺，马文双，李明君，等.工程测量中平面坐标转换软件设计及应用［J］.测绘工程，2013，22（4）：76-79.

［3］ 赵景堂，杜国明，李秀海.基于总体最小二乘法的二维坐标转换方法［J］.黑龙江工程学院学报，2015，29 （1）：21-22，26.

［4］ 韩军生，顾和和.基于2维转换原理的实时坐标转换设计［J］.测绘与空间地理信息，2012，35（1）：164-166.

［5］ 王仲锋，杨凤宝.空间直角坐标转换大地坐标的直接接法［J］.测绘工程，2010，19（2）：7-12.

［6］ 郭英起，唐彬，张秋江，等.基于空间直角坐标系的高精度坐标转换方法研究［J］.大地测量与地球动力学，2012，32（3）：125-128.

［7］ 鲍建宽，李永利，李秀海.大地坐标转换模型及其应用［J］.测绘工程，2013，22（3）：56-60.

［8］ 王文利，程传录，陈俊英.常用坐标转换模型及其实用性研究［J］.测绘信息与工程，2010，35（5）：37-39.

［9］ 马家琼，杨晓英，崔文刚，等.WGS-84与西安80坐标转换研究［J］.测绘与空间地理信息，2013，36（4）：158-160.

［10］许磊，胡圣武.大地坐标与高斯坐标的转换程序研究和精度分析［J］.地理空间信息，2011，9（2）：60-65.

［责任编辑：郝丽英］

Implementation of seven parameters coordinate conversion based on Matlab

LI Zhiwei1，LI Kezhao1，2，ZHAO Leijie1
（1.School of Surveying and Landing Information Engineering，Henan Polytechnic University，Jiaozuo 454000，China；2.Collaborative Innovation Center of BDS Research Application，Zhengzhou 450052，China）

Abstract：The engineering survey，in order to reduce the projection of the problems of large deformation，generally chooses to build its own independent coordinate system.The coordinate conversion between different coordinate system becomes a problem urgently to be solved.In this paper，Matlab 7.0software is used to calculate Boolean Sally seven parameters by the linear least squares fitting function，and the distance between the transformed coordinates and the actual distance measured values of a number of points.Comparing with actual distance measured value in the similar simulation experiment by the steel rule，it can meet the requirements of practical engineering application based on coordinate conversion of Boolean Sally seven parameters.

Key words：ordinate transformation；Matlab7.0；Boolean Sally seven parameters；similar simulation experiment

中图分类号：P226

文献标识码：A

文章编号：1671-4679（2016）02-0001-04

收稿日期：2015-12-07

基金项目：国家自然科学基金资助项目（41202245，41272373）

作者简介：李志伟（1991-），男，硕士研究生，研究方向：大地测量理论与方法.