多连杆式后悬架系统整体强度分析

倪晋挺

（安徽机电职业技术学院汽车工程系，安徽芜湖241002）



多连杆式后悬架系统整体强度分析

倪晋挺

（安徽机电职业技术学院汽车工程系，安徽芜湖241002）

摘 要：有限元法在汽车悬架系统结构件的强度分析中应用广泛，但大多仅针对单个零件进行强度校核，由于系统各部件间是运动关系，载荷及边界条件难以精确确定，对计算结果的准确性造成影响。以某轿车多连杆式后悬系统为例，提出悬架系统整体结构有限元强度分析方法，并以后轴焊接总成在悬架系统中的分析结果与单件分析的结果进行对比，比较其结果的差异性。研究结果表明，由于单件分析连接位置采用固定约束，受到的载荷为集中载荷，导致单件分析的应力水平过高；而系统整体强度分析考虑到各部件间的运动关系，其准确度相对较高。

关键词：多连杆；后悬架；强度分析

多连杆式悬架是应用广泛的一种汽车悬架。汽车悬架的主要作用之一是车轮与车架或车身之间的各种力和力矩的传递，其结构强度的好坏直接影响到车辆的行驶可靠性和安全寿命。多连杆式后悬架系统一般是由后轴焊接总成、控制臂、转向节、拖曳臂、前束拉杆、下横臂、横向稳定杆、弹簧及减震器等组成。长期以来，有限元法对悬架的结构强度分析主要集中于零部件的强度分析，由于悬架系统相邻零部件间存在运动关系，载荷及边界条件难以确定，影响计算结果的准确性［1-3］。

针对上述问题，本文以某轿车多连杆式后悬架为例，提出悬架系统整体结构有限元强度分析方法，建模过程中，不仅要模拟悬架系统相邻部件间的相互运动关系，还要考虑弹簧、减震器、衬套和限位块刚度对悬架系统的影响，完成悬架系统整体结构的强度分析。为了研究整体分析结果与单件分析结果的差异性，以后轴焊接总成在悬架系统中的分析结果与其单件分析时的结果进行了对比，总结出差异的原因［4-9］。

1　有限元建模与载荷工况确定

1.1有限元建模

某轿车多连杆式后悬系统主要由后轴焊接总成、控制臂、转向节、拖曳臂、前束拉杆、下横臂、横向稳定杆、弹簧及减震器等组成，在三维软件CATIA中，根据设计图纸建立其几何模型，如图1所示。在有限元前处理软件HYPERMESH中，完成几何模型各零部件的网格划分，定义材料属性，设置相邻部件间的连接属性和边界条件，生成有限元模型，在有限元软件ABAQUS中进行数值计算。模型中的焊缝处按照连续处理，所用材料属性和母材相同［10-11］。

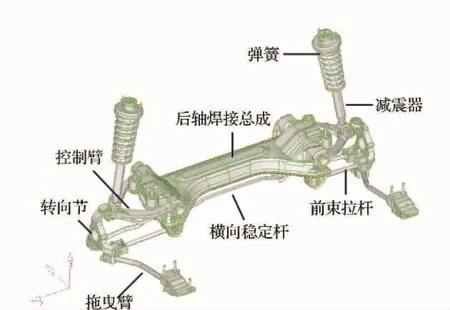
图1　某轿车多连杆式后悬架三维几何模型

为准确反映应力集中情况，建立有限元模型时后轴焊接总成（薄壁板件焊接而成）采用S4（壳单元）模拟，焊点采用BEAM（刚性单元）模拟，而焊缝采用同厚度的壳单元模拟；控制臂和转向节用C3D8（实体单元）建模；拖曳臂、前束拉杆、下横臂、横向稳定杆用B31（梁单元）模拟；弹簧及减震器采用connector（连接单元）模拟；各部件的连接部分均采用不同类型的connector（连接单元）模拟［12-14］。离散化后模型如图2所示，其中全局坐标系为整车坐标系，模型信息如表1所示。

表1　有限元模型信息

1.2载荷工况

行驶的汽车，车轮上承受的载荷大多是随机的，状况非常复杂，且载荷随发动机输出转矩、路面不平度、地面附着系数、行驶速度、车辆载重及驾驶员的操纵等不同而变化，因此，确定典型工况为悬架进行强度校核非常重要。

图2　多连杆式后悬架系统有限元模型

为便于对多连杆式后悬架进行强度校核，依据参考文献［15］，将路面与车轮接触点处的受力状况简化为4种典型的计算工况，即：1）车辆满载行驶于不平路面，受冲击载荷，即最大垂直力工况；2）车辆满载紧急制动，即最大制动力工况；3）车辆满载加速，即最大驱动力工况；4）车辆满载转弯，即车转弯工况。只要这4种典型工况下悬架的强度都能得到保证，就可认为该悬架在汽车的各种行驶条件下都是安全可靠的，计算如下：

1）最大垂直力工况，路面与单侧后车轮接触处的最大垂直载荷FVm可表示为

式中：k2为静强度动载荷系数，如图3所示；FVor为后轮满载的静载荷。

2）最大制动力工况，后轮载荷可表示为

式中：FVor为满载后轮静负荷；FBr为后侧车轮制动力；FVBr为后侧车轮垂直力。

图3　垂直动载荷特性曲线

3）最大驱动力工况，后轮垂直载荷增加，后侧车轮的载荷可表述如下

式中：FA2r为后轮所受纵向力；k1为耐久性垂直动载荷系数，如图3所示；FVA2r为加速时后轮承受的垂直载荷。

4）汽车满载转弯时，其后轮所受载荷如图4所示。左右侧后轮的垂直载荷FZrl，FZrr分别为

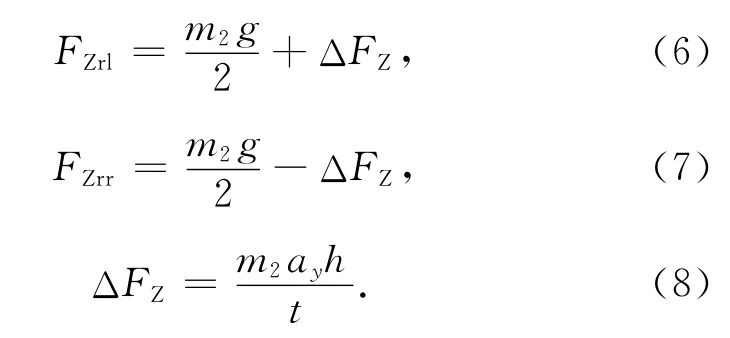
式中：m2为后轴载荷；ay为转弯加速度；h为质心高度；t为轮距。

故左右侧车轮承受的侧向载荷Fyrl，Fyrf分别为

2　整体结构有限元强度分析

某轿车的基本参数：轴距2 700mm、轮距1 550mm；满载时质量为2 075kg（前轴、后轴分别为：1 017kg、1 058kg），质心的高度490mm；轮胎的有效半径370mm；制动盘的有效半径128mm。材料参数：左/右后轴支架、后横拉杆支架、后摆臂左/右连接板、前摆臂连接板和前/后控制臂左/右前连接板的材料均为SPHC，料厚2.5mm；后轴上/下体材料为SAPH370，料厚2.5mm；其它部件材料为QT450-10。材料力学参数如表2所示。

图4　汽车转弯受力

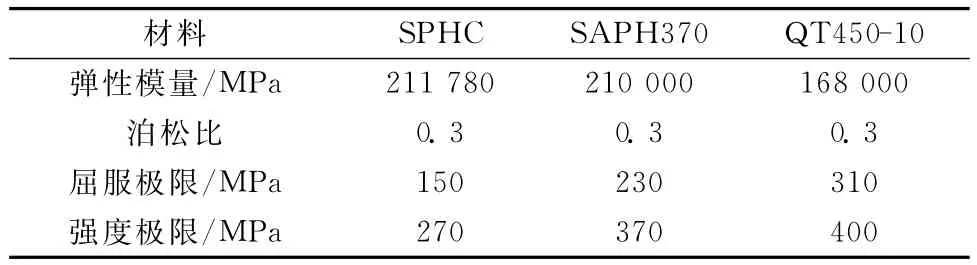
表2　材料力学参数

因轮胎受力比较复杂，大变形、非线性短时间内难以完成，本模型不考虑轮胎的作用，将轮胎接地点的力等效变换到转向节与轮辋的装配点。将副车架与车身连接点的6个自由度全部约束，减震器与车身的连接点约束6个自由度，拖曳臂与车身连接点处约束X，Y，Z3个方向平动自由度，在转向节与轮辋装配硬点施加各工况下车轮的作用力。根据上述工况算得轮辋的装配硬点在各工况下的载荷如表3所示。

表3　轮辋装配硬点在各工况下的载荷

最大垂直力工况，车轮承受冲击载荷，依据图3的垂直动载荷曲线，k2取2.5，由式（1）算得作用于后轮上的垂直载荷为12 287N，如表3所示。其整体结构有限元分析应力云图如图5所示，最大应力为388.5MPa，出现在控制臂与减震器的连接处；后轴焊接总成的应力分布如图6所示，最大应力为332.0MPa，高应力区域集中在控制臂与副车架连接处；控制臂与转向节总成的应力分布如图7、图8所示。最大应力为226.9MPa。满足静强度要求。

图5　多连杆式后悬架系统整体结构应力云图

同理，根据最大垂直载荷工况的计算方法，得到其他3种工况下，后悬系统各主要部件的最大应力值及分布位置。典型工况下后悬架系统各部件最大应力值汇总如表4所示。

表4　主要部件在典型工况下最大应力值

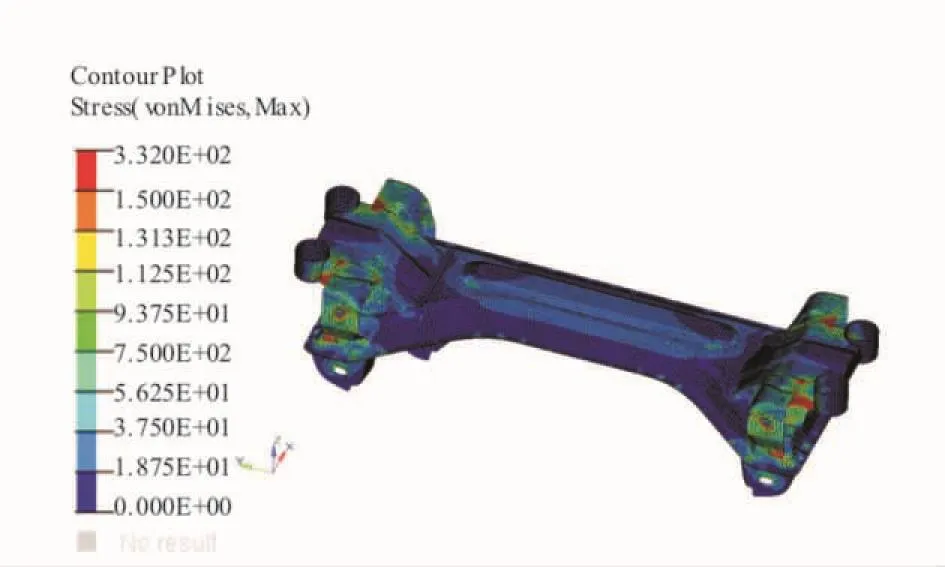
图6　后轴焊接总成在悬架系统中的应力云图

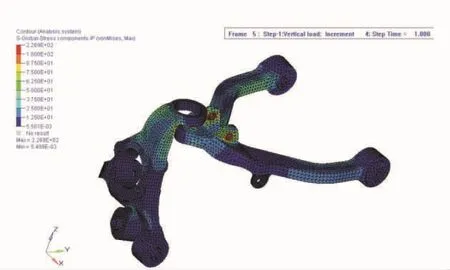
图7　左控制臂与转向节在悬架系统中的应力云图

图8　右控制臂与转向节在悬架系统中的应力云图

通过4种典型工况的计算，在转弯工况下后轴焊接总成及控制臂转向节出现最大应力，都满足静强度要求。

3　对比分析

下面将针对后轴焊接总成在悬架系统中的分析结果与单件分析的结果进行对比，讨论其结果的差异性。图9为后轴焊接总成在工况1下单件分析的应力云图。表5为两种模型的最大应力对比。

由此可以看出，单件分析的应力普遍高于整体分析，工况2和工况3差值较大，其他两种工况差值相对误差达到10%左右。单件分析时部件与车身的连接部位采用全约束，其他连接部件的连接处采用集中力加载的方式，都可能导致单件分析时的应力水平过高。由于悬架整体模型没有考虑轮辋和轮胎的影响，影响了制动力矩的传递，制动力矩对工况2和工况3存在影响，导致这两种工况应力值差别较大。

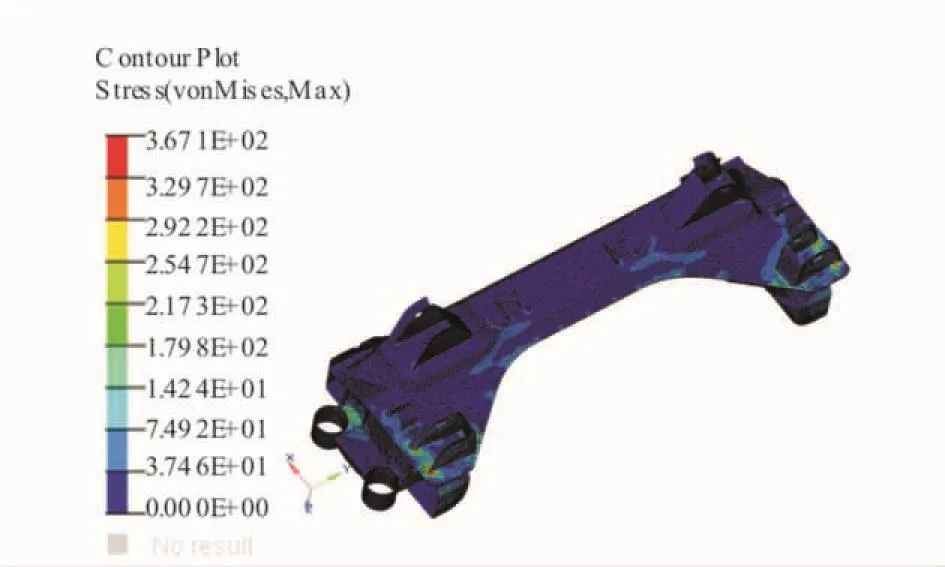
图9　后轴焊接总成单件分析的应力云图

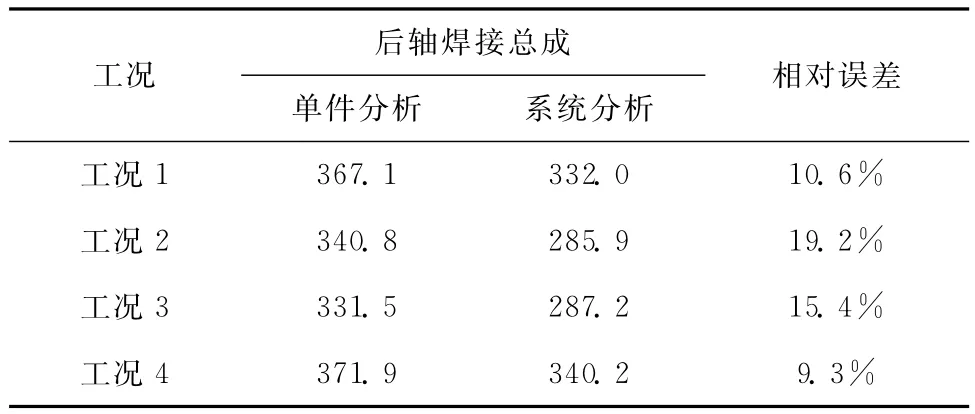
表5　后轴焊接总成两种方案下最大应力值对比

4　结 论

该车型多连杆后悬架系统的后轴焊接总成、转向节及控制臂，在典型工况下均满足静强度要求。后轴的部分区域（焊点和焊缝的应力集中区域）的应力水平高于材料屈服极限，这些区域将出现塑性变形，应给予重视并采取有效措施。后轴焊接总成的焊接部位较多，整个后轴在典型工况下的应力水平较高，建议进行疲劳试验考察结构的疲劳品质。该系统模型中没有考虑轮胎和衬套的影响，计算结果可能存在偏差。

通过对比分析，单件分析的应力水平普遍高于整体分析的应力水平，原因可能是单件分析时没有考虑构件间的运动关系、单件分析的集中力加载方式，都会导致单件分析应力水平较高。悬架整体模型没有考虑轮辋和轮胎，影响了制动力矩的传递，导致工况2和工况3的应力值差别较大。本文对于悬架系统结构件的强度设计具有一定的现实意义。

参考文献

［1］ 李国华，但世群.一种C级车多连杆前悬架的定位参数分析［J］.农业装备与车辆工程，2011，12：26-28.

［2］ 姜欣，唐晓峰，俞斌，等.多连杆后副车架结构及衬套优化设计［J］.计算机辅助工程，2013，22（S2）：226-231.

［3］ 陈家瑞.汽车构造［M］.北京：人民交通出版社，2000.

［4］ 王望予.汽车设计［M］.北京：机械工业出版社，2011.

［5］ 牛礼民，张杰坤，刘超.FSAE赛车双横臂悬架系统机构设计［J］.汽车工程师，2012（9）：31-34.

［6］ 赵雨旸，王春良，杜宏磊.汽车鼓式制动器制动蹄的模态分析［J］.黑龙江工程学院学报（自然科学版），2011 （3）：17-22.

［7］ 齐鹏，崔宏耀，王强.基于UG与ANSYS的节油赛车车架结构分析［J］.黑龙江工程学院学报（自然科学版），2012（1）：32-35.

［8］ 马景军，叶宇天，桂浩，等.大学生方程式赛车（FSAE）悬架优化设计［J］.黑龙江工程学院学报，2015（4）：27-31.

［9］ 吴健瑜，罗玉涛，黄向东.FSAE赛车双横臂悬架优化设计［J］.机械设计与制造，2011（10）：120-122.

［10］胡玉梅，邓兆祥，王欣，等.汽车后悬架的非线性有限元分析［J］.重庆大学学报，2003，26（4）：38-41.

［11］高卫民，王宏雁.汽车结构分析有限元法［J］.汽车研究与开发，2000（6）.

［12］石亦平，周玉蓉.ABAQUS有限元分析实例详解［M］.北京：机械工业出版社，2013：226-276.

［13］黄向东.汽车悬架系统的有限元分析法及其应用［J］.中国机械工程，1994，5（1）：44-45.

［14］王勖成.有限单元法［M］.北京：清华大学出版社，2004：468-518.

［15］王霄锋.汽车底盘设计［M］.北京：清华大学出版社，2010：50-54.

［责任编辑：郝丽英］

Strength analysis of integrated multi-link rear suspension system

NI Jinting
（Department of Automotive Engineering，Anhui Technical College of Mechanical and Electrical Engineering，Wuhu 241002，China）

Abstract：Finite element method is widely used in the structural analysis of vehicle suspension，but the vast majority of applications are limited to individual parts analysis.Boundary conditions and loading are difficult to define because of mutual movement between each component，affecting the accuracy of the calculation results.The paper，taking an automobile multi-link rear suspension as an example，presents a strength analysis method of integrated suspension system.Compared with the result of rear axle welding assemble in the suspension system，it analyzes the single unit and studies the differences.The results show that the stress level of a single piece is too high because of connection position with fixed constrains and by mostly concentrated load.The overall analysis system can fully consider the movement of each component，so the accuracy of the results is relatively high.This method is important for the design and development of suspension system.

Key words：multi-link；rear suspension；strength analysis

中图分类号：U463.51

文献标识码：A

文章编号：1671-4679（2016）02-0016-04

收稿日期：2015-12-03

基金项目：2015院级青年教师发展支持计划教科研项目（2015yjzr027）

作者简介：倪晋挺（1983-），男，讲师，研究方向：汽车悬架.