不等厚板对接焊缝的超声波探伤

钱政平 陈士华 章文显 杨雯青

(中车戚墅堰机车车辆工艺研究所有限公司 江苏 常州 213011)



不等厚板对接焊缝的超声波探伤

钱政平 陈士华 章文显 杨雯青

(中车戚墅堰机车车辆工艺研究所有限公司 江苏 常州 213011)

针对不等厚板对接焊缝的缺陷定位首先采用理论推导方式，分别对斜面、平面入射方式的一次、二次波进行论述，得到定位公式，再通过试块对比和实际检测加以验证，最终证明了公式的正确性和实用性，能够快速定位缺陷。

不等厚；焊板；超声波；缺陷；定位

在焊缝结构中，两侧母材厚度不一致的不等厚焊缝是超声波检测的一个难点。而重要受力部位和过渡区域的特殊部位常采用不等厚板进行对接。由于两侧结构不等厚，焊接时受热不均匀等原因，焊缝更容易产生各种危害性缺陷，并且由于两侧钢板不等厚，探头在斜面上扫查或声束在斜面上反射时，声束的角度会产生变化，确定缺陷的大小和位置就比较困难，特别是不能准确地反映缺陷的位置，造成了很大的返修不便。

在某钢结构桥梁检测中，钢箱梁的两侧均采用了不等厚对接焊缝，按照TB 10212—2009 《铁路钢桥制造规范》中要求，Ⅰ类和Ⅱ类对接焊缝需要进行100%超声波探伤。因此，通过理论计算和实物验证，以得到更为有效的方法，从而实现在不等厚焊缝实际超声波检测中快速定位缺陷。

1 理论分析

由于焊缝较长、结构形状较为复杂等原因，采用单面双侧扫查是比较合理的检测方式。不等厚板材在加工时多将厚板单面加工成斜面，如图1所示，所以在实际检测过程中，也需要考虑到这种情形。为此，对以斜面作为扫查面或者作为反射面2种情况分别进行了理论推导。

1.1 斜面作为扫查面

假定超声波探伤仪按声程定位，探头折射角为β，斜面倾角为α，图1中A点为探头入射点，B点靠近斜面的焊趾位置，F点为焊缝中缺陷反射点位置，T1为薄壁厚度，T2为厚壁厚度。

(1)当采用一次波检验时

图1中AH为斜面法线，AG为平面法线；作BC和FH线，使BC∥FH⊥AG。

由图1可知α=β-β＇

H1=AG-AC=S×cosβ＇-l×sinα

L1=FG-BC=S×sinβ＇-l×cosα

移动探头，即可通过一次波对焊缝进行扫查。

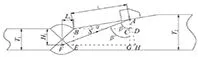
图1 斜面作为扫查面时一次波

(2) 当采用二次波检验时

对于某些类型的缺陷，因为形状、位置等原因，一次波无法扫查时，需采用二次波。如图2所示，AH为斜面法线，AG为平面法线；延长AJ至F点，使FJ=IJ；作BC和FH线，使BC∥FH⊥AG。

图2 斜面作为扫查面时二次波

H2=2T1-(AG-AC)

=2T1-(S×cosβ＇-l×sinα)

L2=FG-BC=S×sinβ＇-l×cosα

式中：H1、L1为一次波检验时，修正后的缺陷深度和水平距离；H2、L2为二次波检验时，修正后的缺陷深度和水平距离；l为超声探头入射点至焊趾B点的距离(即图1、2中AB的距离)；S为超声仪上显出缺陷的声程(即图1、2中AF的距离)。

需要注意的是，以斜面作为扫查面进行二次波扫查时，如果斜面过短，小于1倍跨距时，将无法在斜面上扫查覆盖整个焊缝，这时必须添加在右侧厚板平面上扫查的方式。其理论计算和常规的焊缝检测是相同的，这里不赘述。

1.2 斜面作为反射面

假定超声波探伤仪按声程定位，探头折射角为β，斜面倾角为α，图1中A点为探头入射点，G点为焊缝中缺陷反射点位置，T1为薄壁厚度，T2为厚壁厚度，W为焊缝宽度，l1为探头入射点至焊缝中心的距离。

当采用一次波检验时，与常规对接焊缝的探伤方法一致。二次波检验具体如图3、图4所示。

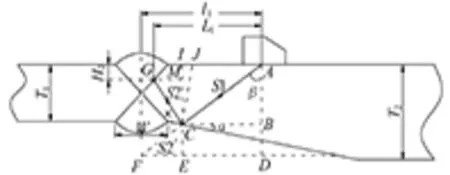
图3 斜面作为反射面时二次波

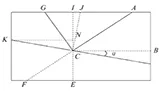
图4 C点局部放大

图3中AD为平面法线，CJ为斜面法线；延长AC至F点，使CG=CF；作EI线，使EI∥AD；作BC和DF线，使AI∥BC∥DF。

由图3、4可知，∠FCE=β, ∠GCM=β-2α；已知现场的斜面倾斜度为1∶4，即tgα=1/4，α=14°。

在△ABC和△KNC中：

BC=AB×tgβ

KN=l1-W/2-AB×tgβ

AB=T1+KN×tgβ

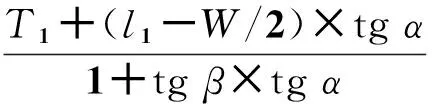
在△EFC和△GMC中：

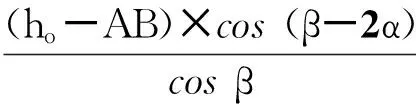
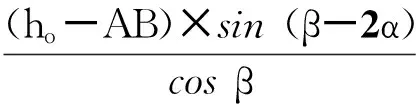
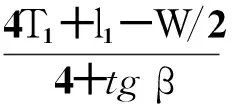
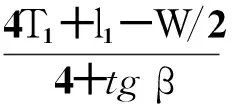
式中：H2为二次波检验时修正后的缺陷深度距离；L2为二次波检验时修正后的缺陷水平距离；ho为超声仪上显出的缺陷深度，即图3中的AD。

由上述公式可以看出，斜面无论是作为扫查面还是作为反射面，超声仪上显示的缺陷深度都小于缺陷的实际深度，而显示的缺陷水平距离要大于缺陷的实际水平距离，即仪器上显示的深度偏小、水平距离偏大，偏差程度将随着斜面倾角α的增大而增大。因此，实际检测前要考虑到这个问题。

2 试验验证

2.1 公式应用

在实际超声波检测过程中可将板厚和斜面长度等已知参数代入公式中，进行简化。例如：已知条件不等厚焊缝的两侧板厚为T1=24mm，T2=40mm，α=14°，W=30mm，选用K2.5探头，即探头折射角β=68.2°，将这些已知数据代入上述公式中。

(1)以斜面作为扫查面时的一次波检验则图1中的参数为：

α=β-β′ 即β′=β-α=68.2-14=54.2

H1=S×cosβ′-l×sinα=0.58S-0.24l

L1= S×sinβ′-l×cosα=0.81S-0.97l

(2)以斜面作为扫查面时的二次波检验则图2中的参数为：

H2=2T1-(S×cosβ′-l×sinα)

=2T1-(0.58S-0.24l)

L2= S×sinβ′-l×cosα=0.81S-0.97l

(3)以斜面作为反射面时的二次波检验则图3中的参数为：

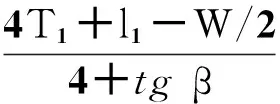
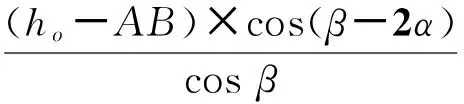
=0.46(81+l1)-5.4ho

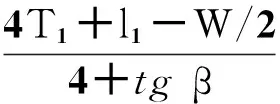
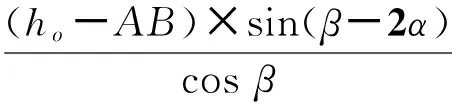
=0.64(81+l1)+4.6ho

这时可以发现，在已知参数的前提下，公式得到了大幅度简化，在实际检测过程中能够立即进行计算或者直接口算，对缺陷进行准确定位。

2.2 试块验证

理论计算和试块法是超声波检测的常见的2种方法[1]。为了更方便地调整不等厚焊缝超声波探伤的灵敏度，对缺陷进行定位，还可以设计、制作不等厚焊缝超声波检测灵敏度试块，如图5所示。

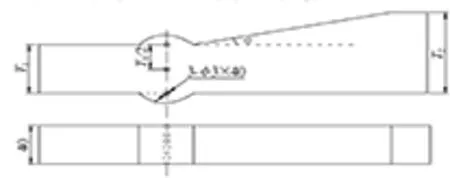
图5 试块

在上述试块上，以斜坡面作为扫查面为例，采用不同角度的探头对人工缺陷进行检测，然后将计算出来的深度、水平距离与试块进行比较，结果如表1所示，误差±1.5mm。这对于定位精度相对较低的超声波检测而言，是一个合理的数据。

表1 ø3 mm 横通孔检测数据 /mm

注：H1、L1为一次波检验时，修正后的缺陷深度和水平距离；H2、L2为二次波检验时，修正后的缺陷深度和水平距离。

3 结论

通过推导公式并简化，结合现场实际操作，证明了以斜面作为扫查面或作为反射面时，一、二次波探伤理论结果的正确性，具有较好的实用性和可操作性，在工程实践中取得了良好的应用效果。

[1] 邓凯斌. 二次波探伤中反射面为斜面时的缺陷定位计算[J].无损检测，2003(6)：311-312.□

(编辑：林素珍)

2095-5251(2016)04-0036-03

2015-12-03

钱政平(1981-)，男，大专学历，高级技师，从事铁路零部件无损检测工作。

TG115.28+5

B