基于相位一致性的冕环识别方法∗

李洪波 赵明宇 刘煜1

(1中国科学院云南天文台 昆明 650011) (2中国科学院大学 北京 100049)

基于相位一致性的冕环识别方法∗

李洪波1,2†赵明宇1‡刘煜1

(1中国科学院云南天文台 昆明 650011) (2中国科学院大学 北京 100049)

尝试将相位一致性方法增强的图像用于冕环结构的识别.针对相位一致性方法增强图像,提出一个新的冕环识别方法(简称PCB),该方法依据冕环形态变化比较平缓的形态学特性,将冕环识别方向限制在一个较小的范围之内,并且首次同时将识别过程中推进方向的变化情况和识别点的相位一致性大小作为终止识别的判据.对多组数据的识别和分析则表明相位一致性方法增强的图像的确适合用于冕环识别,而PCB方法所识别的冕环结构则同时具有很好的完整性和准确性,是一套现实可行的冕环自动识别方法.

太阳:日冕,技术:图像处理,方法：观测

1 引言

冕环作为日冕中主要的X射线发射源,被认为是由磁场束缚的热等离子体形成的亮环状结构[1].因此冕环的结构很好地反映了日冕的磁场结构,同时也是光球层和日冕之间的能量通道.冕环普遍存在于日冕层,可被大量的空间卫星探测到,对冕环的研究有利于我们更好地理解日冕中等离子体的特性[2-3].关于冕环的基本性质和其演化规律却一直未被很好地理解[4].首先各种冕环的分类标准还没有很好地建立起来.初期Vaiana等[5]依据冕环的形态学特性为标准,将冕环分为亮点冕环、活动区冕环和大尺度冕环.随着多波段观测数据的日益丰富,更详细的温度和密度研究得以展开.由于不同温度冕环的温度和密度性质明显不同,例如暖冕上不同位置的温度大致相同,而热冕环则不同,另一种新的基于温度的分类方法被提出,依据温度的不同将冕环分为冷冕环[6]、暖冕环、热冕环[7]3种.不同温度冕环温度和密度特性的不同也暗示着这些冕环可能产生于不同的物理机制[8].至于不同种类的冕环产生的具体物理机制以及它们是否可以相互转化等基本问题,都未被很好地解决[9].另外,由于目前直接测量日冕磁场非常困难,对冕环几何形状的研究在探索日冕磁场结构和日冕中磁重联方面也有着很重要的参考意义.大体上看,冕环呈现出对称的环状结构[10],比较特别的是冕环的横截面沿着冕环有着很小的变化[11],这与我们通常使用的日冕中的无力场假设所预期的结果有些不同,无力场外推结果预测磁场结构的截面将会有几倍的扩展.基于这个问题,有不同的冕环模型被提出,但是还没有任何一个模型可以解释所有的问题.值得注意的是,由于我们的观测结果是一个投影效果,所以冕环的真实形状的研究也有一定的难度,而“日地关系观测台”(Solar Terrestrial Relations Observatory,STEREO)[12]的发射为我们提供了多角度太阳观测数据,这使得我们可以更好地重构出三维冕环结构[13].除此之外,冕环内部的等离子体流动[14–16],以及磁流体波动在冕环中的传播等问题[17–19],都没有被很好地理解.更加详细的研究,以及更加深入的学习,毫无疑问都需要大量的样本,这就需要我们对冕环进行大量准确的识别和提取.

自从冕环结构被发现以来,已经有多个团组对冕环结构的提取以及自动识别方法展开研究,并提出了几种不同的冕环识别方法.主要的冕环自动识别方法基本上包括两个主要的过程:首先要对原始图像进行处理从而使冕环结构更加突出,或者对属于冕环结构的点进行标记;第2步就要通过一些边缘连接或者边缘检测程序对处理过的图像中的冕环结构进行提取和识别.早在2006年Lee等[20]就首先提出了一种基于方向连通性(oriented connectivity)的自动冕环识别方法(简称OCM).这种方法首先将原始图像进行锐化,然后用Strous提出的边缘检测方法1h ttp://www.lm sal.com/aschw and/stereo/2000easton/cdaw.h tm l对锐化图像中的冕环结构进行标记,而接下来对标记的冕环结构进行识别连通时,作者建设性考虑了磁场的物理特性,并用一个磁场模型来指导接下来的识别过程.测试结果则表明OCM方法识别的冕环有着很好的完整性,识别的冕环也比较光滑.但是可能由于磁场模型本身和冕环实际情况之间的差别,以及第1步边缘检测的结果连续性较差而且噪点较多等因素的影响,尽管识别过程中两次使用样条拟合(sp line fitting),该程序所识别的冕环数目还是偏少.另外由于两次人为拟合,也导致OCM方法的灵敏度变得很低,有时候甚至会将相邻的冕环识别为一个冕环.之后Aschwanden等[21]也提出一种冕环识别方法(简称ODM),该方法直接用冕环结构提升处理之后的图像作为参考进行第2步的冕环结构识别,之后在沿着预测方向一定距离(假设5像素)附近一个较大的盒子(假设10 pixel×10 pixel)里面进行搜索,该预测方向是通过对每一个搜索盒子里最大值的位置进行线性回归拟合(linear regression fitting)得到,将该窗口内最大亮度值以及窗口内最大亮度位置到该方向的距离两个参数用作停止识别的判据.由于采用更直接的冕环增强图像作为参考和新的识别方法,使得Aschwanden等的ODM冕环识别方法可以识别较多的冕环结构,但是测试结果也表明该方法也存在一定的不足,即抗噪声能力较差,识别过程很容易受到噪声影响.这使得其识别的冕环完整性较差,此外其结果也存在一些错误识别的小结构.

目前已经有多种针对边缘结构提取的方法被开发出来,但是多数方法是针对一个更加广泛的范围,而专门针对冕环结构提取的方法则相对较少.因此在2008年Aschwanden等[21]将现有的5种对边缘结构进行自动识别的方法进行了对比.除了前文介绍的两个方法以外,他们还介绍了3种不同的结构识别方法.其中包括Lee等[20]开发的Dynam ic Aperture-based Loop Segmentation(简称DAM)方法,这种方法主要的特点是通过沿冕环的强度曲面是连续的高斯曲面这样的假设来进行冕环的检测和识别.该方法首先搜索图像中符合高斯曲面的结构视为冕环结构,接着将结果中相邻的结构依据拟合参数的相似情况进行连接,最后还要对不是冕环的结构进行剔除.这种DAM方法的结果则同前面介绍的OCM的结果类似,由于有连接的过程,所以识别的冕环会比较完整,但是其同样存在灵敏度较低的问题,识别的冕环数目也比较少.文中另外介绍的一个冕环识别方法是Steger等2Steger L H.Techn ica l Rep ort FGBV-96-03,Forschungsgruppe B ildverstehen(FG BV),In form atik IX, Techn ische Un iversit¨at M¨unchen,G erm any,1996提出的一种边缘探测方法(简称UDM),该方法已经被成功地用于遥感、医学等多个领域.在这种方法中曲线结构的识别是基于该结构垂直方向的二阶导数来实现的,这样可以减小结构宽度以及不对称性的影响,这种方法的结果则同Aschwanden的ODM方法类似,有着较好的灵敏度,可以识别出更多种类的冕环,但是识别冕环的完整性则较差,其识别结果同样存在一些奇怪的小尺度结构.除此以外Aschwanden等[21]还介绍了一种自动探测的方法(简称RAS)[22],这种方法是Inhester等人通过改进Parent等[23]的边缘探测方法得到的,其主要是用图像的泰勒级数(Taylor coefficient)来确定冕环点的位置、方向等参数.测试表明该方法不但可以识别不同种类的冕环结构,而且识别的冕环也比较完整,但是RAS的识别暗条的末端有时会存在一些错误弯曲,同时也会错误地识别一些小尺度的非冕环结构.Aschwanden的研究将这5种现存的不同冕环结构识别方法应用于“过渡区和日冕探测器”(Transition Region and Coronal Exp lorer,TRACE)[24]的171˚A波段观测图像中,对提取的结果进行了详细的比较.结果表明尽管5种算法都可以得到大致相同的结果,但同人工识别的结果相比,这些结果间还是存在着不可忽略的差异.因此如果想得到更好的结果,仍然需要更加详细的研究[21].

值得注意的是,前面我们介绍的大量关于冕环自动识别的工作主要是优化冕环自动识别工作的第2个步骤,针对冕环标记、边缘连接和识别方法进行研究优化,而对原图像进行处理从而提高冕环结构对比度方面则没有太多的方法改进.在这方面M cAteer等[25]测试了一种基于小波变换的冕环探测方法(简称W TMM),他们尝试利用小波变换方法对冕环结构进行增强,并且针对TRACE在171˚A波段的观测图像进行了研究.结果表明利用多尺度频域信息增强后的冕环结构具有很好的方向连通性,可直接提取感兴趣尺度信息等天然优势,但这种方法也存在着对较暗结构的提升效果较差、识别准确性较低等问题.类似于M cAteer等[25]的小波变换的方法,相位一致性同样是基于图像多尺度频域信息的结构增强方法,不同的是该方法主要利用图像的相位一致性反映图像的结构信息、受到结构对比度影响小等特点来提取图像的结构特征. Feng等[26]在2014年关于相位一致性方法在探测低对比度太阳结构方面的研究则很好地表明相位一致性方法在增强日冕边缘冕环结构方面有着很大的优势.基于相位一致性方法的这些特性,我们发现相位一致性方法在冕环图像处理方面的应用非常值得进一步研究,因此我们对相位一致性方法在冕环结构提取方面的应用进行了进一步的研究,并且提出了一个新的基于相位一致性的冕环识别方法.

2 相位一致性方法

研究表明图像的结构特征更多地包含在图像的相位谱之中,早在1981年Oppenheim和Lim[27]就做过相关的实验.试验中作者首先将两幅图像进行傅里叶变换分别计算出相位和振幅谱,然后将两幅图的功率谱进行交换并且反变换之后发现得到新的图像与为其提供相位谱的图像非常相似,而与为其提供功率谱的图像有很少相似之处.

在结构识别的研究中,Morrone和Owens[28]将相位一致性定义为:

其中PC(x)代表x点的相位一致性,An(x)为x点第n个傅里叶分量的振幅,E(x)是x点上各个傅里叶分量的矢量和.它的几何描述如图1所示,一维信号F(x)在x处每一个傅里叶分量都有一个振幅An(x)和相位ϕn(x),这些傅里叶分量作为复矢量按照平行四边形法则加起来,得到从原点到终点的复矢量振幅|E(x)|,相位一致性就是这个总振幅与各个傅里叶分量振幅之和的比值.显然如果所有傅里叶分量相位角都相等,则PC(x)=1,而各个傅里叶分量相位完全不相干,则PC(x)趋近于0.

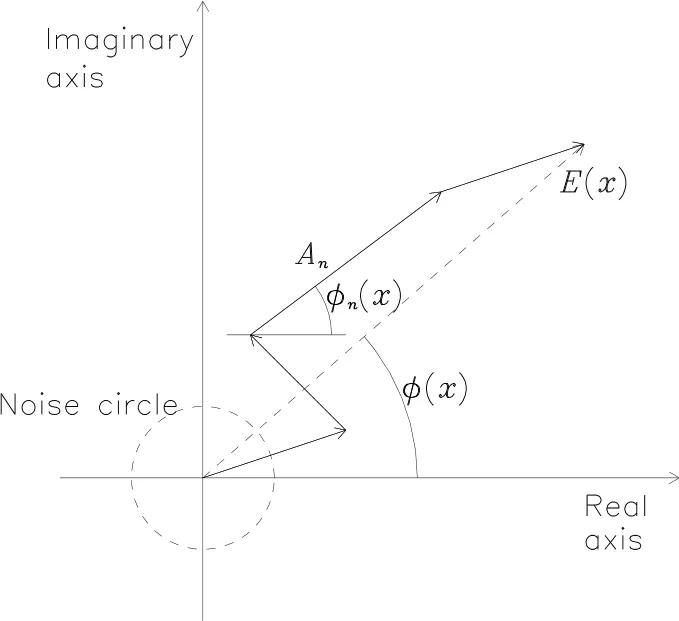
图1 相位一致性的几何描述[29]Fig.1 Geom etric descrip tion of the phase congruency[29]

值得注意的是,这里的相位一致性仅仅在一个较宽的频域范围内才有意义,如果某一个振幅分量远远大于其他振幅分量,则相位一致性结果总是趋近于1.因此Kovesi在相位一致性的计算公式中乘入了一个权重函数,从而得到了相位一致性新的表达式[29-30]:

这里∆ϕn(x)=cos(ϕn(x)−ϕ(x))−|sin[ϕn(x)−ϕ(x)]|,而T是估计的噪声,ε为一个小量,为了防止分母为零的情况出现,w(x)即新加入的权重因子,它的表达式为:

其中γ为增益因子,用来控制截止函数的陡峭程度,c则是一个截止参量,如果f(x)小于c则PC的值将被限制变小.N是滤波函数尺度的总个数,Amax(x)是各阶傅里叶分量振幅的最大值.

上面主要描述的是一维信号的处理方式,而对于二维图像的相位一致性,目前有两种方法可以计算:一个就是方向滤波方法[29-30],另外一个则是单演滤波方法(Monogenic Filter)[31].这里我们采用的是Felsberg和Sommer提出的单演滤波方法[31].该方法在频域中引入滤波函数:

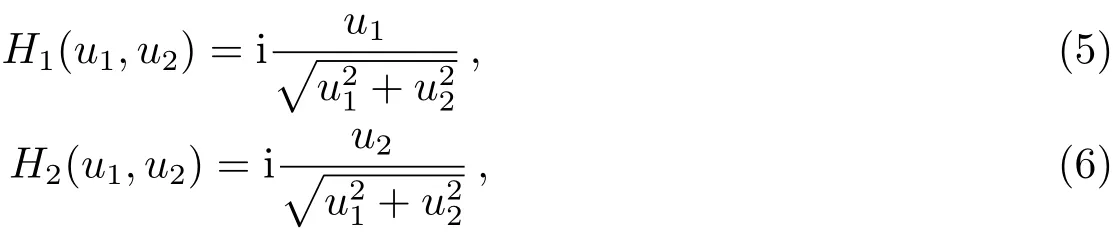
式中i为虚数单位.为了减少计算量,这里引入滤波函数H,使H满足

这里采用频域中Log-Garbor作为基础函数对图像进行滤波,Log-garbor函数如下:

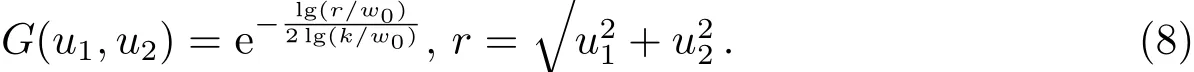
单演滤波方法是首先利用Log-Garbor对图像进行滤波得到滤波后的信号f(x,y),之后利用滤波函数H对f(x,y)进行滤波得到滤波后的信号f h(x,y).将f(x,y)的实部fr(x,y),和f h(x,y)的实部f hr(x,y)和虚部f hi(x,y)组合到一起,我们就得到了一组二维的“解析信号”:

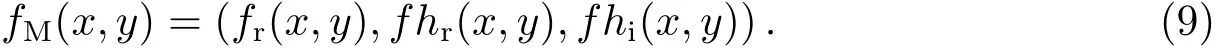
我们称之为单演信号,在球坐标系下ϕ∈[0,2π),θ∈[0,π),则有

因此单演信号的局部振频(Local Amplitude)为:

局部相位(Local Phase)为:

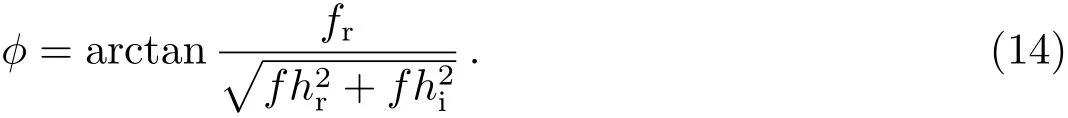
局部方位(Local Orientation)为:

图像总的振频|E|、相位角ϕ、方位角θ分别为:

这里n代表不同的尺度,这样单演滤波的相位一致性就可以根据(2)式得到,图像特征结构越明显,它的相位一致性和总相位角也就越大,而方位角则分别反映图像中这些特征结构的方向性.

图2展示了一幅冕环图像,该图显示的是搭载在“太阳动力学天文台”(Solar Dynamics Observatory,SDO,2010)[32]上的“大气成像组件”(Atmospheric Imaging Assembly, AIA)[33]在2015年6月18日00:00:11 UT 171˚A波段观测数据.该图的空间分辨率为0.6′′,图中数据已经经过了标准的AIA PREP校准过程.从图2中我们可以发现多数冕环结构的亮度从足点到拱顶逐渐下降,导致冕环结构的清晰度从足点向上逐渐降低,最终在接近冕环顶部附近的冕环变得模糊难辨;另外我们也可以注意到大部分冕环结构有着一定的透明度,导致冕环的亮度变化更加复杂;还有部分冕环结构互相交叉,在它们交叉部分冕环的走向变得难以分辨,这都为冕环结构的识别带来了巨大挑战.接下来我们分别利用高通滤波(high pass filtered)、巴特沃思带通滤波(band pass filtered)、高斯带通滤波、基于单演滤波的二维相位一致性方法对图2中的测试图像进行处理,结果如图3所示.其中(a)、(b)、(c)分别是高通滤波、巴特沃思带通滤波、高斯带通滤波的结果,这里高通滤波是利用原图减去它的16×16 boxcar平滑结果所得,巴特沃思带通滤波、高斯带通滤波使用IDL函数库里面的BANDPASS FILTER程序实现,其中巴特沃思带通滤波的阶数为20,巴特沃思和高斯带通滤波的频带范围为最高频率的0.05–0.25倍.图3的(d)、(e)、(f)为相位一致性方法所得到的相位一致性PC、相位角、方位角,计算过程中我们应用了单演滤波的方法,利用(8)式所给出的Log-Garbor函数作为基函数进行滤波,不同尺度滤波函数中的中心波长的取值为λ0=3×2.1n(这里中心波长的单位是像素),式中不同的n代表不同尺度的滤波函数,这里我们取n=0,1,2,3 4个尺度滤波函数.从结果我们可以看出相位一致性方法的确可以很好地对复杂环境下的冕环结构进行增强,尤其是相位角(如图3(e)所示)可以很好地突出测试图中的冕环结构.进一步对比表明在相位角图像中整条冕环对比度明显有着较大提高,尤其是冕环顶部较暗的部分对比度得到了很好的提升.

图2 SDO卫星171˚A波段的冕环图像.为了更加清晰地显示图像细节,图中颜色越黑代表辐射越强.虚线S0展示了图4中的亮度变化曲线所在的位置.Fig.2 The coronal loop im ages observed by SDO 171˚A.B lack m eans h igh fluxes in th is im age to show the details.T he dashed line S0 ind icates the location of the p rofiles in Fig.4.

为进一步对比不同图像增强方法的效果,我们把几种不同方法得到的S0(如图2中黑色虚线所示)上的亮度变化曲线展示在图4之中.如图4所示S0中明显有3个峰值分别代表3个冕环结构.从原图亮度曲线(黑色实线)上我们可以看出,3个冕环中中间冕环有着较好的对比度,而两边的冕环则比较暗;从相位一致性相位角结果(绿色点线)我们可以看出,相位一致性方法对于S0两边的暗冕环结构的提取结果同中间亮冕环结构达到同一水平,而其他方法对暗结构的提取结果则明显差于相位一致性的结果.总体而言,相位一致性相位角图像不但可以很好地提取亮冕环结构,同时也可以很好地提取较暗冕环结构.最后我们注意到相位一致性方法也存在着一定的问题:它在增强了冕环结构的同时,也对其他的一些非冕环结构和噪声进行了增强.

3 冕环识别算法

从我们的测试图像可以看出,冕环结构有着亮度变化大,以及相互交叠等特点,这都对冕环识别提出了很大的挑战.但是通过大量的观测分析我们也发现冕环结构基本上都是较光滑的大尺度结构,它们多数是从活动区磁极发出并且有着很好的连续性,尽管随着高度增加亮度会有明显降低,但是形态变化却很平滑,主要由椭圆形的闭合冕环和放射状的开放冕环构成,这些特征则对冕环的识别非常有利.

图3 利用高通滤波、带通滤波以及相位一致性算法进行冕环结构增强所得到的结果图像Fig.3 T he coronal loop structu res strengthened by h igh pass filtered,band pass filtered,and phase congruency detective m ethods,resp ectively

为了更好地识别冕环结构,我们在ODM方法的基础上发展了一个专门针对极紫外波段观测到的冕环图像进行优化的算法.该算法主要是依据冕环形态变化比较平滑的特性对冕环识别过程进行优化得到的.改进后的算法是通过冕环的方向性来指引识别过程,而冕环的方向则是通过计算以初始点为中心的上下两个180°扇面上各方向亮度平均值的分布确定.这个扇面的半径即我们的搜索半径(简称rs),rs的取值应该大于冕环的宽度,依据不同的情况可取冕环宽度的几倍,我们在计算过程中取35像素.基本的计算过程为,首先计算预期方向周围180°扇面上各个方向的亮度平均值,将亮度大于最大亮度95%的方向进行平均从而得到该点的推进方向,并将识别结果沿该推进方向推进一段较小的距离(该距离就是推进步长,默认为2像素),之后循环这个过程从而对图像中的冕环结构逐步识别.直接使用这个算法则会遇到与ODM相同的问题,使得识别过程很容易被噪声打断,从而导致识别的结构不完整.针对这个问题,我们对上述算法进行了一些改进,其详细过程如图5所示.图中两个交叉的黑色弧形环代表我们要识别的冕环结构,其中一条环上的白色星线为我们已经识别的部分冕环结构,已经识别的冕环的切线方向为该点的预期方向(如图5中绿色箭头所示).这样如果计算过程进行到冕环交叉的地方,或者冕环外面有一些亮度较大的噪声点时,我们的算法将会识别出两处或多处亮度较大的方向,图中红色扇面就标出了两处不连续的亮度较大方向.如果将这两处方向共同进行平均就很容易得到一个错误的方向,使推进点脱离冕环结构,最终导致识别提前结束.这种情况下由于冕环的形态变化比较平缓,因此下一点上冕环方向不会有太大的变化,所以这里我们只取预期方向周围较小范围(计算过程中默认为±10°)内的亮度满足条件的方向进行平均.如果我们预期的结果可能出现的范围内没有满足条件的方向或者整个搜索范围内找到的亮度满足大于最大亮度95%的方向总的个数超过一定范围(我们计算过程中默认为方向总个数的1/3),则按照预期方向进行推进并且将该次识别记为一次异常识别.

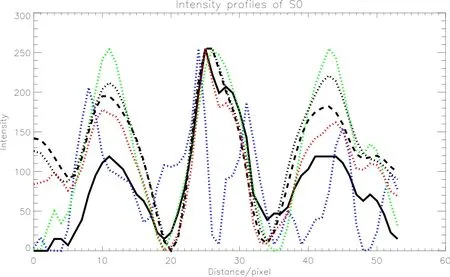
图4 S0上的亮度变化曲线,其中黑色实线为原始数据,蓝、绿、红色3条点线分别为利用单演滤波得到的相位一致性PC、相位角图像以及高通滤波所得图像的结果,而黑色点线以及虚线则是巴特沃思带通滤波和高斯带通滤波所得到图像的结果,这里所有结果都被等比例归一化到0–255.F ig.4 The in tensity p rofiles of S0.The b lack so lid line ind icates the origina l data.T he b lue,green,and red dotted lines show the data got from PC im age,im age,and high pass filtered im age,respectively. The Bu tterw orth and G ausssian band pass filtered resu lts are show n by the b lack dotted line and the b lack dashed line,resp ectively.Notew orthily,all the resu lts are norm alized to 0–255.

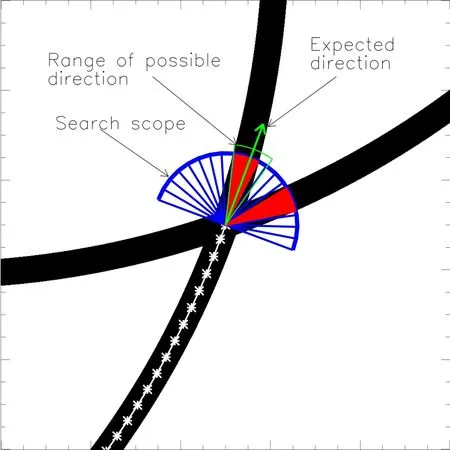
图5 冕环识别算法示意图.其中绿色箭头为预期的冕环方向,其周围较小的绿色扇面为我们程序所允许的结果方向的范围,蓝色180°扇面则是我们的搜索范围,红色扇面则是具有较大平均亮度的两个方向范围.Fig.5 The schem atic of ou r loop-tracing m ethod.The green arrow ind icates the expected d irection. A round th is green arrow,the sm aller green sector and 180°b lue sector are the range of p ossib le resu lt a llow ed by ou r p rogram and the search ing scop e,resp ectively.T he red sectors ind icate the tw o ranges of d irection along w h ich p ixels have a larger m ean intensity.

4 冕环自动识别方法

基于相位一致性所得到的冕环增强图像和经过改进的冕环识别算法,我们提出了一个新的冕环自动识别方法(Phase-congruency-based method,简称PCB方法).这个方法主要通过两个步骤进行冕环自动识别.首先我们通过一个程序对原始日冕观测图像进行预处理,该过程要先对原始图像进行分块,每一块子图的平均值要大于一定的阈值mi(我们的计算中默认取值为0.05,代表图像最大值的0.05倍),则认为该块图像中可能存在冕环结构.如果存在冕环结构则将该块子图中的最大值所在的位置标记为一个初始点,这些点将被用作下一步冕环结构识别的初始点,接下来该程序则会应用相位一致性方法对原始图像进行冕环结构增强.经过实验,我们发现针对AIA和TRACE望远镜171˚A波段的观测数据,取λ0=3×2.1n(n=0,1,2,3)像素的4个不同尺度的滤波函数进行计算所得到的相位角图像,即可使绝大部分的冕环结构得到很好的增强,因此我们将以该图为参考进行第2步的冕环识别.第2步,我们将依据第1步所得到的冕环增强图像和初始点进行冕环识别,识别过程中主要用到我们改进过的冕环识别算法对每一个初始点进行冕环的识别.这里我们首次将识别方向的改变情况以及识别结果点的亮度共同用于判断识别结果的正确性,如果连续zn次识别结果(默认zn=2)均为异常识别或者识别结果点的亮度低于我们提前设定的截止阈值toff(默认为0.3,代表图像最大亮度的0.3倍),则认为识别已经超出真正的冕环结构并且终止本次识别.最后我们的程序将识别的长度大于30像素的结构进行记录,而更短的结构则认为是其他结构,不进行任何记录.

另外,我们也注意到前面的程序将可能在同一个冕环结构上产生多个初始点,这样将会导致同一冕环被重复识别多次,在我们识别方法中提供了两个办法解决这个问题.第1种方法(简称为PCB1)是每次识别开始时我们就判断该初始点与前面所识别出来的冕环上所有点的距离的最小值,如果小于我们设定的阈值(简称mw,默认为25像素),我们就将该初始点剔除,不再进行识别.考虑到第1种方法中如果阈值mw设定得太小,则还是会有少量重复识别结果,设定得太大时,可能错误地剔除部分靠得较近的相平行的冕环,因此我们提出了第2种方法(简称PCB2).该方法是将每一个新识别的点同前面所有结果的距离的最小值都计算出来,如果小于我们设定的另一个阈值(简称md,默认为6像素)的点数超过3个则终止识别.这里以图3中的测试图像为例,以默认的参数进行识别,第1种方法中的mw取值为25,第2种方法中的md则取为6,它们的结果如图6所示.图中星状点代表我们所得到的初始点,粗线代表程序识别的冕环结构,两种方法在相同电脑上所用时间分别为3.463 s和8.502 s.经过对比我们可以发现这两种方法基本上都可以有效地去除重复识别的结果,但是从图6中上图的效果看第1种方法的结果中还有少量重复识别发生,因此剔除效果可能稍微差于第2种方法,但是从计算速度上看其比第2种方法要快.

值得注意的是,终止识别的条件的选取一直是一个复杂的问题,如果取得过于苛刻则不能很好地识别较暗的冕环和一些冕环中较暗的部分,如果取得过于宽松则亮结构冕环的识别容易超出其边界,得到错误的识别结果,这导致准确性和完整性很难同时都获得.但是由于超出冕环后的错误识别结果不再具有很好的连续性,所以超出后的识别方向会有剧烈的波动.根据这些特点我们首次将识别方向的变化情况用于判断是否停止识别,这样我们就可以进一步将原来的条件放宽松.试验表明较小的亮度截止阈值toff加上较小的方向改变阈值zn可以很好地弥补之前较宽松的截止亮度阈值产生的错误识别结果,而且可以得到更加完整平滑的冕环结构,这些都使得我们的识别结果更加接近真实情况.

5 识别结果的比较和分析

针对冕环的特性和相位一致性方法所得到的冕环增强图像的特点,我们提出了一个新的PCB冕环识别方法.为了更好地同其他方法进行对比,这里我们采用Aschwanden等[21]和M cAteer等[25]所用的测试数据对我们的方法进行测试,测试中所用的参数均采用前文给出的默认值.TRACE的这组数据如图7所示,该数据是TRACE卫星在1998年5月19日22:21 UT 171˚A波段的观测结果.利用PCB2方法所得到的识别结果展示在图8之中,图中我们可以看到PCB2识别的冕环整体上都比较完整,而且识别的冕环结构都比较光滑,尤其是对图像两边的开放冕环的识别有着很大的优势,接下来我们通过一些定量参数以及局部区域结果对PCB2的具体特性进行详细分析.

图6 两种不同的避免重复方法的识别结果.上下两图分别显示PCB 1和PCB 2所识别的结果.Fig.6 T he iden tified resu lts of tw o m ethods that are used to avoid rep eating iden tifications.Top (bottom)panel is the resu lt of PCB 1(PCB 2).

5.1 完整性分析

冕环识别结果的完整性可以分为两个方面:首先是识别的冕环种类完整,其次就是识别出来的冕环的长度完整.由于各个不同方法的识别结果都含有大量的冕环,而且识别结果的位置也各有不同,所以很难对其完整性进行直接对比.根据Aschwanden等[21]所采用的一种方法,我们可以通过识别的长度大于L的冕环总数随L的分布(简称冕环累积分布)来大致反映冕环识别结果的完整度.该参数既反映了识别冕环的长度,又反映了冕环的数量.为了对比PCB2方法识别结果的完整性,我们也计算出了我们的PCB2方法识别结果的冕环累积分布,分布结果展示在图9之中.图像表明我们的方法识别出了96条长度大于70像素的冕环,与Aschwanden等[21]探测到大于70像素冕环最多的RAS方法所得到的结果91条水平相当.除此之外,为了更全面地反映我们的方法识别冕环的完整性,我们也将识别结果同Aschwanden等[21]的结果(图3、图4、图5)进行详细对比.一方面从识别的种类上看,PCB2方法所识别的图像中间部分的闭合冕环和两侧的开放冕环几乎同Aschwanden等[21]所提到的OCM、DAM、UDM、ODM 4种方法的总和相当;另一方面在识别冕环的长度上,我们的识别结果在闭合冕环的顶部并没有像UDM和ODM那样发生中断,而在两边开放冕环的顶端,我们的方法则可以将大多数开放冕环识别到接近图像边缘,这方面PCB2方法对开放冕环的探测结果甚至比Aschwanden等[21]所提到的5种方法都要好.

图7 TRACE 171˚A波段于1998年5月19日22:21 UT观测数据.与前面A IA的图像相同,图中颜色越黑代表辐射越强.Fig.7 T he corona l im age observed by the TRACE 171˚A at 22:21 UT on 1998 M ay 19.Notew orthily, b lack m eans h igh fluxes in th is im age.

图8 TRACE数据的冕环自动识别结果Fig.8 The coronal loops autom atically ex tracted from the tested TRACE im ages

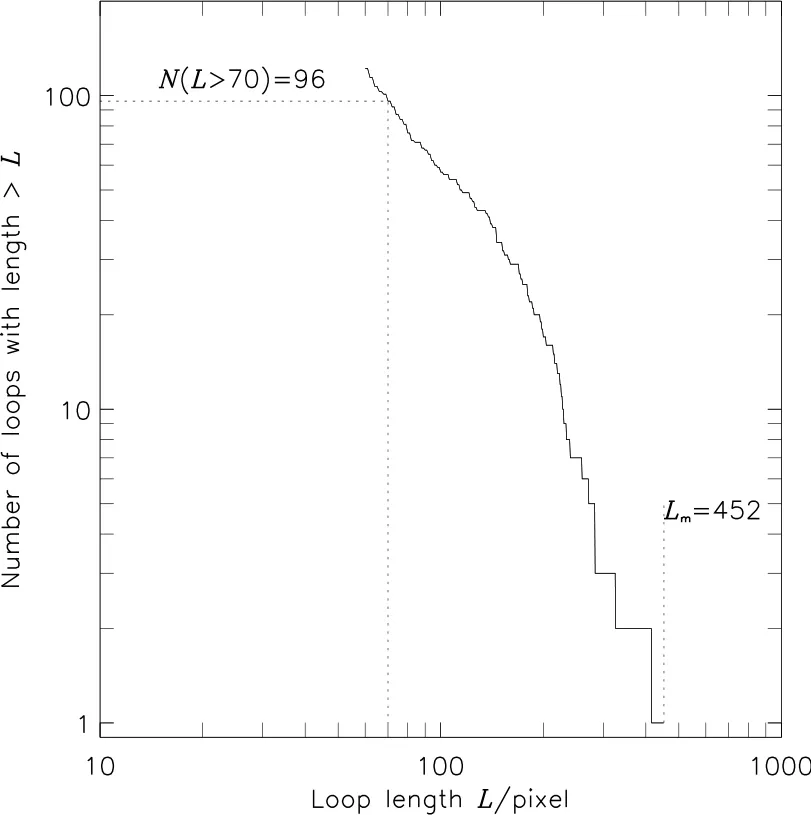
图9 TRACE数据识别中冕环长度大于L的累计分布图Fig.9 T he cum u lative d istribu tion of loops iden tified from the tested TRACE im age with a length larger than L

5.2 准确性和灵敏度分析

为了对冕环识别结果的准确性和灵敏度进行详细的比较分析,我们选取了图像中A、B两个小区域来进行详细对比,该区域同Aschwanden等[21]所选取的区域完全相同.图10和图11分别展示了我们选取的A、B两个区域,两幅图的背景是该区域高通滤波图像的等高线,里面的粗线即为PCB2方法的识别结果,图中等高线密集的地方就是冕环所在的位置.通过对比识别结果和等高线的位置关系,我们就可以知道识别结果是否准确,如果识别的冕环和背景等高线分布密集的地方符合得较好,则说明识别的结果比较准确.从图10和图11的结果我们可以看到,PCB2方法识别冕环结构与背景等高线很好地符合在一起.同文献[21]中的结果相比,可以看出我们的结果有以下特点:首先,PCB2的结果同OCM和DAM比较类似,比较光滑,不像UDM那样识别结果有着许多小的虚假振荡;其次,结果冕环末端也比较平滑,这一点要优于RAS的结果;最后,识别结果中错误识别水平也很低.通过对图像中子区域识别结果仔细对比分析,我们可以看出PCB2冕环识别方法的结果同OCM、DAM、UDM、ODM、RAS相比处于一个较准确的水平.而灵敏度方面,PCB2方法可以识别出两个区域中绝大多数的冕环结构,识别的数目和完整性同灵敏度较高的RAS处于同一水平,但是准确性方面却弥补了RAS识别的冕环末端存在少量错误的弯曲和错误识别一些小尺度的非冕环结构两方面的不足.由于PCB2方法在完整性以及准确性方面的优势,尤其是对开放冕环识别方面的良好结果,我们可以发现PCB2方法的确是一个有效可行的冕环识别方法.

图10 TRACE数据A区域的详细识别结果Fig.10 The detailed ex traction resu lt of the TRACE tested data in region A

图11 TRACE数据B区域的详细识别结果Fig.11 The detailed extraction resu lt of the TRACE tested data in region B

6 典型样例中的应用和分析

由于SDO卫星的发射,使得我们可以获得大量的日冕观测数据,这里我们也将PCB2方法用于更多的SDO/AIA 171˚A波段的观测数据之中.首先我们选取了4个典型的冕环观测数据用来测试和分析我们的方法,数据的详细信息如表1所示,测试之前几组数据已经经过标准的预处理过程.数据1–4在撒点过程中的阈值mi分别取为0.03、0.02、0.03、0.02(该阈值的选取既要保证识别较多的结果,又不能包含太多的虚假结构),冕环识别过程中所需要的搜索半径rs和推进步长,以及防止重复识别的阈值md,还有用于停止识别的阈值toff和zn分别取前面给出的默认值.对表1中数据进行冕环识别的结果如图12和图13所示,其中图12上下两图分别展示了测试数据1和数据2的结果,测试数据3和测试数据4的结果则分别展示在图13中的上下两图.在每一幅结果图像中,粗线就是PCB2方法的识别结果,图像的背景为原始观测数据,叠加在背景上的等高线与图10和图11相同,为高通滤波后图像的等高线.与本文第5章的方法相同,我们可以通过分析图像中闭合冕环和开放冕环顶端的识别情况来判断识别结果是否完整,对比结果图像中等高线的位置和识别冕环的对应情况来反映识别结果的准确性.首先我们可以发现PCB2方法的识别结果的确和图像等高线的分布有着很好的对应,因此可以确定PCB2方法的识别结果有着很好的准确性,其次从识别种类上看,不管是较直的开放冕环,还是有一定弧度的闭合冕环,都可以被PCB2方法所识别.通过对识别出的冕环结果进行分析,我们还可以看到不管是较亮的足点部分还是较暗的冕环顶部都可以被较好地识别.但是我们也注意到结果中存在少量将其他结构误识别为冕环的情况,这些误识别结构是位于冕环外围谱斑附近一些大尺度并且较狭窄的亮区域,这些区域同较暗的冕环结构很相似,因此比较容易被误识别.

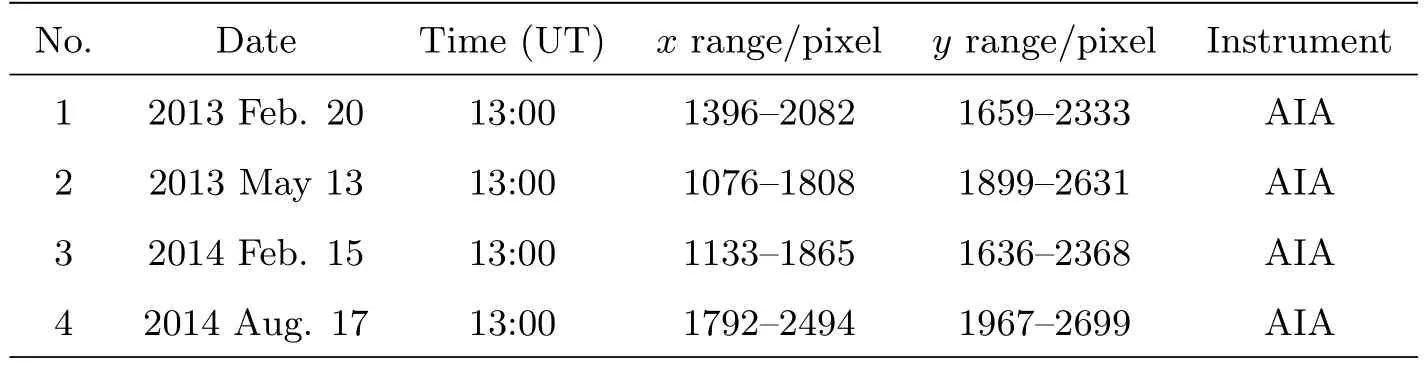
表1 测试图像的详细信息Tab le 1 The detailed in form ation of the test im ages

7 总结与讨论

冕环是日冕中普遍存在的由磁场束缚的热等离子组成的亮环状结构[1],它很好地反映了我们平时很难直接观测到的日冕中的磁场结构[34].大量的观测数据表明多数冕环都处在一个复杂的环境中,而且其本身的亮度也有着很大变化,这都为我们识别冕环结构带来了很大的挑战.针对冕环结构的自动识别,目前已经有一些办法被提出,这些方法都可以在一定程度上得到较好的结果,但是也存在着一些不足.这些冕环识别的方法一般包含对原图像中的冕环结构进行增强,以及对增强结果进行冕环标记识别两个过程.而在2014年Feng等[26]就对利用相位一致性方法来增强日冕中冕环结构的方法进行了详细研究,结果表明相位一致性的确对日冕中的冕环结构有着很好的增强作用,但是基于相位一致性冕环增强图像的冕环识别方法却一直没有被提出.本文我们将相位一致性中单演滤波方法所得到冕环增强图像用于冕环识别之中,提出了一种基于相位一致性的冕环自动识别方法.同时我们也将冕环结构识别算法依据冕环形态变化比较平滑的结构特性进行了改进,只取预期方向周围较小范围内的方向作为有效方向来计算真正的推进方向.最后我们对多组冕环的观测数据进行测试和分析,测试的结果表明我们的方法的识别结果不但具有很高的完整性,而且同时具有较高的准确性,这是大多数方法所不能同时具备的.而且测试结果也表明PCB2方法对大尺度冕环结构有着很好的识别效果,尤其在大尺度开放冕环结构的识别方面有着明显的优势.以上结果表明相位一致性方法增强的冕环图像的确可以被用于冕环结构识别,而我们针对相位一致性增强图像所开发的冕环自动识别方法也确实可以得到比较好的识别结果,是一套现实可行的冕环自动识别方法,对冕环的探索和研究都有一定的使用价值.

图12 PCB 2方法在A IA数据样本1(上)和2(下)中识别的冕环结果Fig.12 The loops detected by PCB 2 from the A IA sam p les 1(top)and 2(bottom)

图13 PCB 2方法在A IA数据样本3(上)和4(下)中识别的冕环结果Fig.13 The loops detected by PCB 2 from the A IA sam p les 3(top)and 4(bottom)

此外我们也注意到,相位一致性方法增强的日冕观测图像中的一些噪声和非冕环结构也同时被增强,针对这样的情况我们提出了一个综合的冕环自动识别方法来减少这些被增强的噪声和非冕环结构对识别过程的影响.在PCB算法中我们主要通过3个方面共同作用来避免识别图像中的非冕环结构.首先我们选取初始点时就对初始点周围一个小范围内的平均值有一定的要求,平均值要大于我们设定的阈值mi才有可能成为一个初始点,这是因为冕环观测图像中真正的冕环结构通常都比较亮,而其他一些亮斑或者非冕环结构周围都比较暗,所以阈值mi的设定可以帮助我们有效地排除多数的噪声以及非冕环结构.第2个方面就是我们将识别方向的改变情况以及识别结果点的亮度共同用做停止识别的判据,如果连续zn次方向识别结果均为异常或者识别点的亮度小于阈值toff则终止识别.这主要是相位一致性增强后的冕环结构有着很高的对比度和连续性,而其他的噪声或者非冕环结构则不同,相比冕环结构图像中的冕环结构,它们一般没有规则的形状,连续性较差,方向改变也较大.因此zn和toff两个判据的共同限制也可以帮助我们排除大部分的非冕环结构.最后我们还要将识别结果的长度做为一个标准来降低错误识别的可能性,这是因为真正的冕环结构属于较大尺度的结构,因此在长度上要远长于大部分的其他结构.值得注意的是,虽然经过这3个步骤的共同作用已经将错误识别的概率降到了很低的水平,但是依然可能有极少量的非冕环结构被识别,这些结构同活动区外边缘较暗的冕环结构很相似,因此很难被区分.

最后应该指出的是,虽然我们提出的冕环识别算法主要是针对相位一致性方法进行优化,但是这个算法也为其他方法的优化提供了参考.我们的结果表明,冕环结构本身的特性为我们进一步优化冕环识别方法提供了一个很好的参考.而且我们也注意到我们的方法也存在少量错误识别等一些问题,因此在这些方面还需要更深入的研究.

[1]Vaiana G S,Reidy W P,Zehnp fennig T,et al.Science,1968,161:564

[2]M oortel I,Nakariakov V M.RSPTA,2012,370:3193

[3]Parnell C E,De M oortel I.RSPTA,2012,370:3217

[4]Go lub L,Noci G,Poletto G,et a l.A p J,1982,259:359

[5]Vaiana G S,K rieger A S,T im othy A F.SoPh,1973,32:81

[6]Foukal P V.A p J,1976,210:575

[7]B rekke P,K jeldseth-M oe O,Harrison R A.SoPh,1997,175:511

[8]Huang Z,Frazin R A,Land i E,et a l.A p J,2012,755:86

[9]Rea le F.LRSP,2014,11:4

[10]A schw anden M J,N itta N V,W¨u lser J P.A p J,2008,680:1477

[11]Go lub L,Nystrom G,Heran t M,et al.Natu re,1990,344:842

[12]Kaiser M L,Kucera T A,Davila J M,et al.SSRv,2008,136:5

[13]张雪飞,刘煜,申远灯,等.天文学进展,2012,30:159

[14]U ritsky V M,Dav ila J M,V iall N M,et a l.A p J,2013,778:26

[15]李海东,赵丽,梁红飞,等.天文学报,2013,54:27

[16]Li H D,Zhao L,Liang H F,et a l.ChA&A,2013,37:266

[17]W ang T,ofm an L,Davila J M.Ap J,2013,775:L23

[18]张真,何馨,梁红飞.天文学报,2013,54:39

[19]Zhang Z,He X,Liang H F.ChA&A,2013,37:428

[20]Lee J K,Newm an T S,G ary G A.Pattern Recogn it,2006,39:246

[21]A schw anden M J,Lee J K,G ary G A,et a l.SoPh,2008,248:359

[22]Inhester B,Feng L,W iegelm ann T.SoPh,2008,248:379

[23]Parent P,Zucker S.IEEE Trans,1989,11:823

[24]Handy B N,A cton L W,K ankelborg C C,et a l.SoPh,1999,187:229

[25]M cA teer R T J,K estener P,A rneodo A,et a l.SoPh,2010,262:387

[26]Feng S,Xu Z,W ang F,et a l.SoPh,2014,289:3985

[27]Oppenheim A V,Lim J S.P roceed ings of the IEEE,1981,69:529

[28]M orrone M C,Ow ens R.Pattern Recogn ition Lett.,1987,6:303

[29]Kovesi P.V idere:Journal of Com pu ter V ision Research,1999,1:1

[30]K ovesi P.Psycho logica l Research,2000,64:136

[31]Felsberg M,Somm er G.M ustererkennung 2000,22.DAGM-Sym p osium.London:Sp ringer-Verlag, 2000:195-202

[32]Pesnell W D,T hom pson B J,Cham berlin P C.SoPh,2012,275:3

[33]Lem en J R,T itle A M,A k in D J,et a l.SoPh,2012,275:17

[34]Rosner R,Tucker W H,Vaiana G S.A p J,1978,220:643

A N ew Coronal Loop Identified Technology Based on the Phase Congruency Detective M ethod

LIHong-bo1,2ZHAO M ing-yu1LIU Yu1

(1 Yunnan O bserva to ries,Chinese A cadem y of Scien ces,K unm ing 650011) (2 Un iversity of Chinese A cadem y of Scien ces,Beijing 100049)

We test a phase congruency method for automatically extracting coronal loops from the coronal observation data,and propose a new coronal loop detective method.On account of smooth changes of the direction along coronal loops,the possib le direction of loops is restricted in a sm all range for im proving the detective result. Beyond that,inspired by the structural characteristics of coronal loops,we firstly suggest that both the change of result directions and the flux of resu lt points can be used to term inate the loop detection.Finally,several coronal images are detected by our loop extracting method,and the result indicates that the congruency enhanced im age is exactly suitable for coronal detection and extraction,and our new loop detective method can also extract most of loops in the test im ages com p letely and accurately. Besides that,our research also suggests that the characteristics of coronal loop should be a significant reference for im p roving other loop detectivemethods.

sun:corona,techniques:im age processing,methods:observational

P182;

A

10.15940/j.cnki.0001-5245.2016.04.003

2015-11-24收到原稿,2016-03-15收到修改稿

∗国家自然科学基金项目(11533009)资助

†hbli@ynao.ac.cn

‡m yzhao@ynao.ac.cn