多任务Sparse G roup Lasso特征提取与支持向量机回归在恒星大气物理参量估计中的应用∗

高伟 李乡儒

(华南师范大学数学科学学院 广州 510631)

多任务Sparse G roup Lasso特征提取与支持向量机回归在恒星大气物理参量估计中的应用∗

高伟 李乡儒†

(华南师范大学数学科学学院 广州 510631)

多任务学习(Mu lti-task Learning,M TL)就是把多个问题一起进行分析、计算,以发掘不同问题之间的相关性,提高分析结果的精度,该类方法已被广泛地应用于机器学习、模式识别、计算机视觉等领域.使用多任务学习方案研究了恒星大气物理参数中表面温度(Teff)、表面重力加速度(lg g)、化学丰度([Fe/H])的估计问题.首先使用多任务Sparse G roup Lasso算法提取对3个大气物理参数均有预测能力的光谱特征;然后使用支持向量机估计恒星大气物理参数.该方案在Sloan实测恒星光谱和理论光谱上均做了测试.在实测光谱上的平均绝对误差分别为:0.0064(lg(Teff/K)),0.1622(lg(g/(cm·s−2))), 0.1221 dex([Fe/H]).在由Kurucz的New Opacity Distribution Function(NEWODF)模型得到的理论光谱上也做了同样的特征提取和恒星大气物理参数估计测试,相应的平均绝对误差分别为:0.0006(lg(Teff/K))),0.0098(lg(g/(cm·s−2))),0.0082 dex([Fe/H]).通过与文献中的同类研究比较表明,多任务Sparse Group Lasso特征提取与支持向量机回归(support vector machine regression,SVR)两者结合的方案有较高的恒星大气物理参量估计精度.

恒星:基本参数,方法:数据分析,方法:统计,方法:其他诸多方面

1 引言

随着现代科技的飞速发展,美国的Sloan数字巡天望远镜[1]获得了大量的光谱数据,而我国的郭守敬望远镜——大天区面积多目标光纤光谱天文望远镜(LAMOST)[2]更是目前世界上光谱获取率最高的望远镜,一次观测可同时获得多达4000个天体的光谱,使人类观测天体光谱的数目提高到千万数量级.

海量恒星光谱数据的获得,使精确、快速地从中估计恒星的3个大气物理参数——表面温度(Teff)、表面重力加速度(lg g)与化学丰度([Fe/H])成为一个很值得探讨的研究课题.我们知道,来自遥远太空的天体光谱的数据量巨大,在传输的过程中会受到大量的噪声干扰,比如大气环境、杂散光、宇宙射线等,在接收时还会受到仪器的不稳定、系统误差等噪声干扰.这些因素会严重影响我们对恒星大气物理参数估计的精度和速度,所以应先对光谱数据进行预处理,降低数据量,提高速度,并减少噪声干扰,然后用提取出的光谱特征估计天体的大气物理参数.

前述数据预处理在模式识别、数据挖掘等领域称之为特征提取.典型的特征提取方法有基于神经网络的多层自编码、主成分分析(Principle Com ponent Analysis, PCA)[3−4]、Lasso[5−6](Least Absolute Shrinkage Selection and Operator)等.特别是, Tibshirani在1996年提出的Lasso算法,该方法是通过对未知的系数向量施加一个l1范数约束,使得绝对值较小的系数自动缩小到0,达到变量选择和特征提取目的.不过, Lasso方法有两个局限性:第一,同一个光谱数据中包含着所有的光谱物理参量的信息量,而不同的光谱物理参量之间又有潜在的关系,所以上述方法把3个恒星大气物理参量分开考虑,对光谱数据进行降维提取光谱特征,会造成各个不同物理参量之间的信息量的损失,进而导致预测精度降低;第二,分开处理3个物理参量的方式繁琐耗时、效率低.

实际上要把3个恒星大气物理参量一起考虑对光谱数据提取特征就是一个多任务学习的问题.多任务学习(M u lti-task learning,MTL)就是在多个任务一起学习中挖掘不同任务之间的关系信息量,同时又能区分不同任务之间的差别,进而能够提高预测模型的预测精度及泛化性能的一种方法.本文使用的多任务Sparse G roup Lasso[7–11],实际上也是改进于上述的Lasso方法及研究组变量选择的Group Lasso[12].它不仅继承了Lasso的优势,能够有效地剔除不重要的组,还克服了Group Lasso不具有组内稀疏性的弊端,可以灵活地选择组内变量,更重要的是还具备做多任务的特征提取的能力,也弥补了上述方法的两点不足,所以可以提高恒星大气物理参数的估计精度.

2 多任务Sparse G roup Lasso特征提取

在光谱数据的多任务学习中,假设有N条恒星光谱,每条光谱由P个流量描述,且有M个恒星大气物理参数需要估计(本文中M=3).记X为一个N×P维输入的光谱数据变量,xj=(,···,)T是X的第j列的流量变量.记Y为响应的N×M维的大气物理参量,ym=(,···,)T是Y的第m列的大气物理参量.对于每一列响应的大气物理参量,假设一个线性模型为

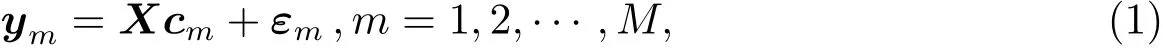
其中cm=(,···,)T是P维的回归系数,εm=(,···,)T是N维的对应误差.为了同时计算M个任务的回归系数向量,即C=(c1,···,cM),需要优化的多任务Sparse Group Lasso模型为

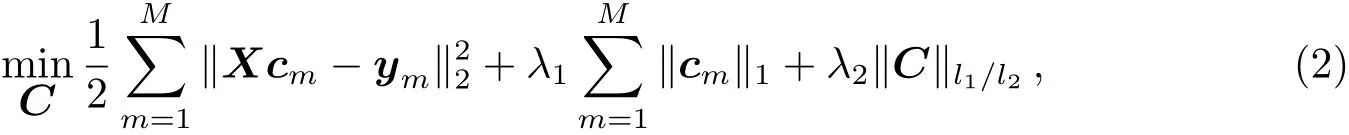
其中‖C‖l1/l2=∑‖(,···,)‖2,‖·‖1表示向量的1范数:求向量所有元素的绝对值和,‖·‖2表示向量的2范数:求向量所有元素的平方和,再开方.在这里C的每一行形成一个组.当M=1时,λ2=0,上式就是Lasso;λ1=0,上式就是Group Lasso.该方法的正则化参数λ1不仅控制整个模型的稀疏性,且控制着任务内的稀疏性,正则化参数λ2不仅控制着任务间的稀疏性,且控制着不同任务的信息保留程度.

3 支持向量机回归

支持向量机是一种典型的统计学习算法,广泛地应用在文本识别、人脸识别、语音识别、时间序列预测等领域.它是建立在Vapnik等人提出的统计学习理论、结构风险最小准则之上,最初是作为一个分类机器提出来的学习方法.支持向量机回归支持向量用于回归问题中的情况,其核心思想是通过核函数间接进行非线性变换来实现非线性的支持向量函数拟合.

由于高维度光谱数据的结构复杂性、非线性,本文中采用的是非线性支持向量机回归.假设待估计的恒星大气物理参数有效温度、表面重力或化学丰度用y表示,相应的多任务Sparse Group Lasso特征用x表示,则支持向量机回归模型为:

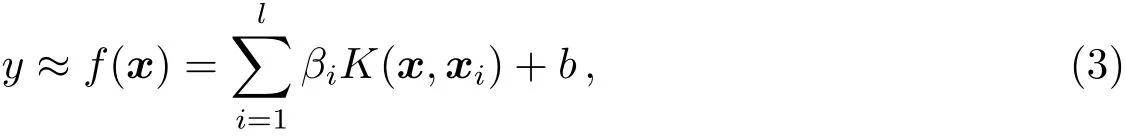
其中K(∗,∗)是非线性的高斯核函数,即

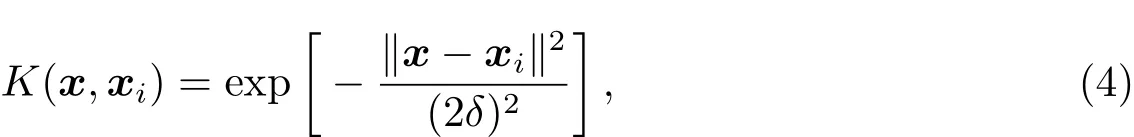
系数βi=−αi,i=1,···,l是以下优化问题的解:

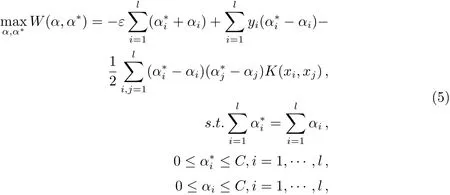
其中,ε是控制拟合误差的一个精度,即误差限,常数C控制着对超出误差限样本的惩罚与函数的平坦性之间的折中.

4 光谱数据与估计准则

本文在Sloan的实测数据和理论恒星光谱数据上均做了实验,验证了方案的可行性,共两个实验.

实验1:数据是美国大型巡天项目Sloan发布的SDSS实测光谱数据中的50000条光谱及每条光谱对应的3个光谱物理参量,分别是表面温度(Teff)、表面重力加速度(lg g)和化学丰度([Fe/H]).每条光谱具有3821个流量特征.3个物理参量的范围分别为:Teff:[4088, 9740]K,lg(g/(cm·s−2)):[1.015,4.998],[Fe/H]:[−3.497,0.268]dex.其中20000条光谱数据作为训练数据,剩下30000条光谱数据作为测试数据.

设训练集为

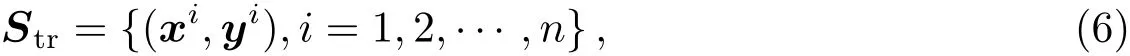
其中xi=(,···,)T∈Rp×1代表第i条光谱数据,yi=(,···,)T∈Rm×1代表第i条光谱数据所对应的m个光谱物理参量.令(Xtr,Ytr)代表训练光谱数据及每条光谱所对应的物理参量,其中

实验2:数据是由Kurucz的NEWODF模型得到的理论光谱中的18969条光谱数据.每条光谱具有3821个流量特征.3个物理参量的范围分别为:Teff:[4000,9750]K,lg (g/(cm·s−2)):[1,5],[Fe/H]:[−3.6,0.3]dex.其中8000条作训练数据,另外10969条作测试数据,对其也做同实验1数据的对应记法及下面的数据预处理.

4.1 数据预处理

(1)为了减小波动范围,精确地描述表面温度(Teff),实验中用温度参量的以10为底的对数lg Teff代替温度参量(Teff).记

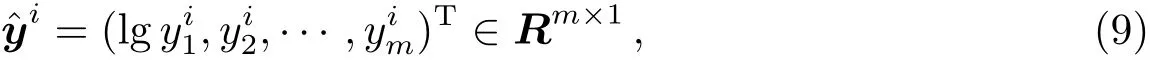
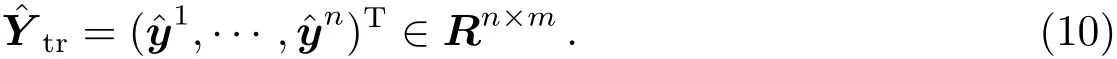
(2)对光谱数据Xtr的每列求均值和标准差,然后中心化,最后标准化.记

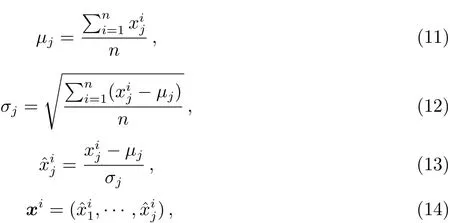
其中i=1,···,n,j=1,···,p.则(7)式转变为

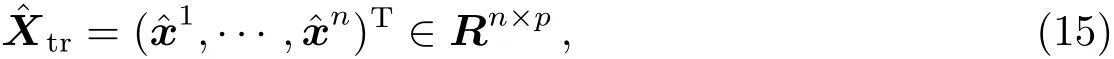
训练集(6)式转变为

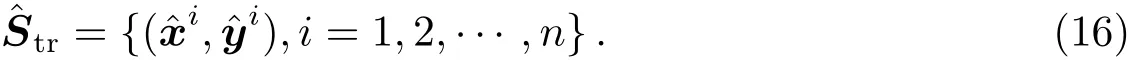
测试集Ste也做同上处理为te={(i,i),i=1,2,···,n},同时得到te,te.

4.2 估计准则

为了更好地评价恒星大气物理参量估计的效果,把估计值与观测值作平均绝对误差(Mean Absolute Error,MAE)、平均误差(Mean Error,ME)和标准偏差(Standard Deviation,SD):

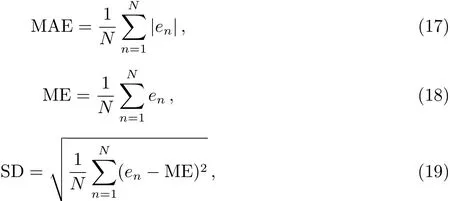
其中en是第n条光谱的物理参量的估计值与观测值之差.

5 实验结果与分析

5.1 实测光谱的结果与分析

在实验1中,主要有3个操作步骤:第1步对光谱数据进行预处理,第2步用多任务Sparse Group Lasso提取光谱流量特征,第3步用支持向量机回归(SVR)对表面温度(Teff)、表面重力加速度(lg g)与化学丰度([Fe/H])进行估计.

本实验不仅估计出3个主要物理参量的平均绝对误差(MAE)、平均误差(ME)与标准偏差(SD),而且列出一些相关文献方法的结果作比较,具体实验与相关文献的结果见表1.更重要的是分别检测出3个物理参量的特征:表面温度(Teff)36个、表面重力加速度(lg g)109个、化学丰度([Fe/H])136个,具体见图1及其具体位置见表2.另外,画出参量误差随Teff、lg g、[Fe/H]的变化情况,具体见图2.

在表1中,相关文献中的研究方法SVRG、ANN与MAχ都是非线性拟合方法, SVRl与OLS是线性拟合方法,明显非线性拟合的结果要比线性拟合的结果好,这也说明恒星光谱数据与3个物理参量之间的函数关系更可能是非线性关系,尤其是与表面重力加速度(lg g)、化学丰度([Fe/H])的函数关系.这也是本文采用非线性的支持向量机回归(SVR),核函数为高斯函数作估计的原因之一.在实验过程中,发现对表面温度(Teff)的预测是最容易的,化学丰度([Fe/H])次之,表面重力加速度(lg g)是最难预测的,表1中3个物理参量相应的预测结果刚好也印证了这一点.

从平均绝对误差(MAE)相较很小可以看出,本文采用的多任务Sparse Group Lasso特征提取与支持向量机回归(SVR)相结合的方案的预测结果要优于相关文献中的线性与非线性方法的预测结果,特别是对表面重力加速度(lg g)与化学丰度([Fe/H])的预测;从平均误差(ME)几乎趋于0能够看出本文方法的系统误差要比相关文献方法的小;实测光谱本身含有相当多的各种噪声,而本文方法预测结果的标准偏差(SD)却相对很小,说明预测结果波动很小,此方法抗噪能力不错,鲁棒性好.

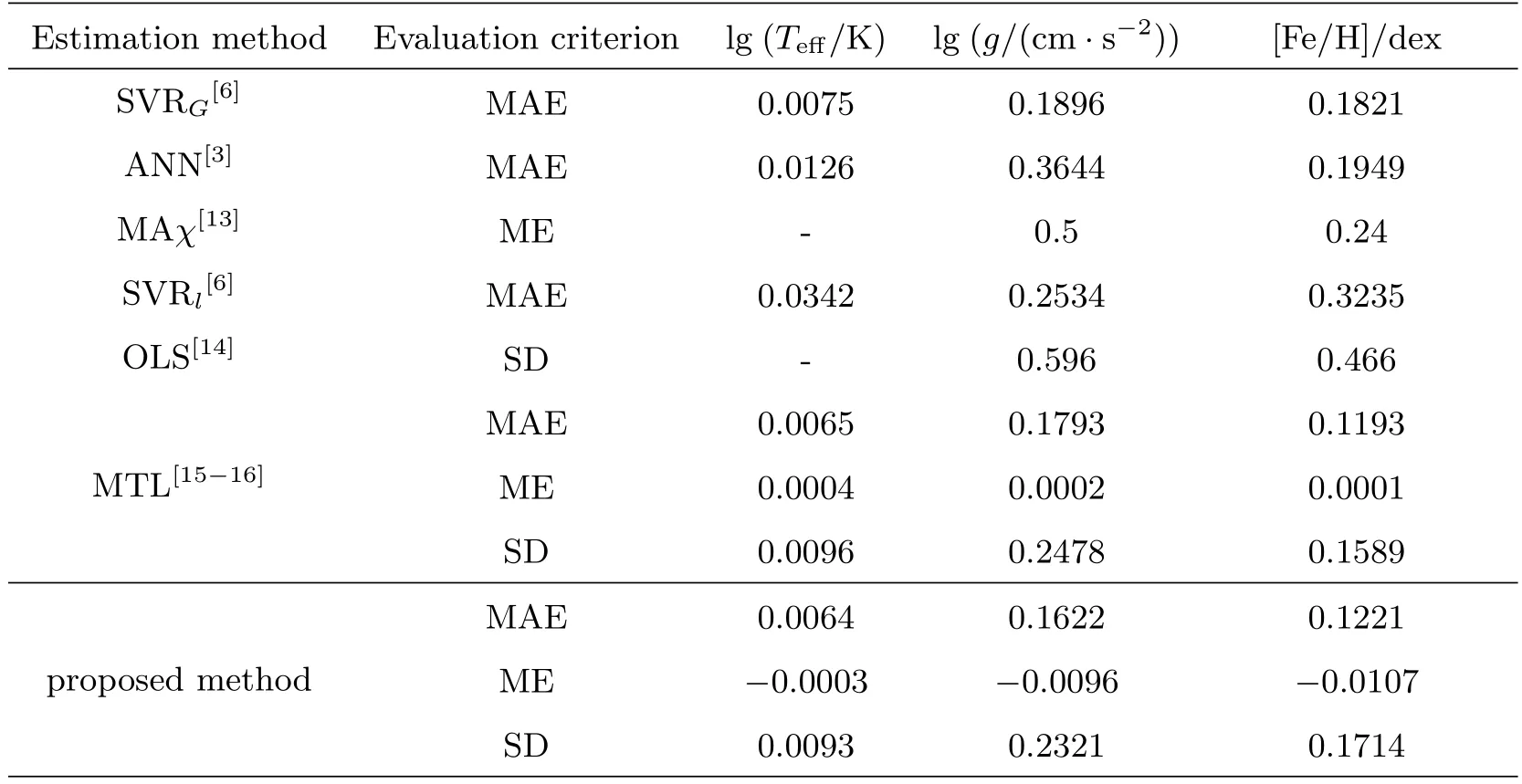
表1 本文方法和文献中典型方案在SDSS实测光谱数据上的实验结果Tab le 1 Ex p erim en tal resu lts of the p rop osed m ethod an d som e ty p ica l schem es in the literatu re on SDSS sp ectra

在文献[6]中SVRG方法与本文的拟合方法是一样的,而特征提取的方法不同.在文献[6]中采用系数压缩法Lasso,是把3个物理参量分开单独进行特征提取,而未对3个物理参量同时提取特征,这样导致不同的光谱物理参量之间潜在的关系信息量的损失,进而影响预测结果.本文使用的多任务Sparse G roup Lasso是系数压缩法Lasso的改进方法,克服了上述弊端,另外多任务方法同时作特征提取也节省了科研时间,提高了效率.从表1中的预测结果也可以看到,此法确实比系数压缩法Lasso适合光谱特征的提取.

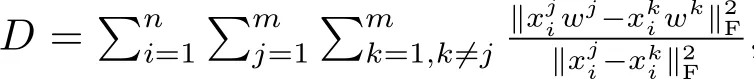
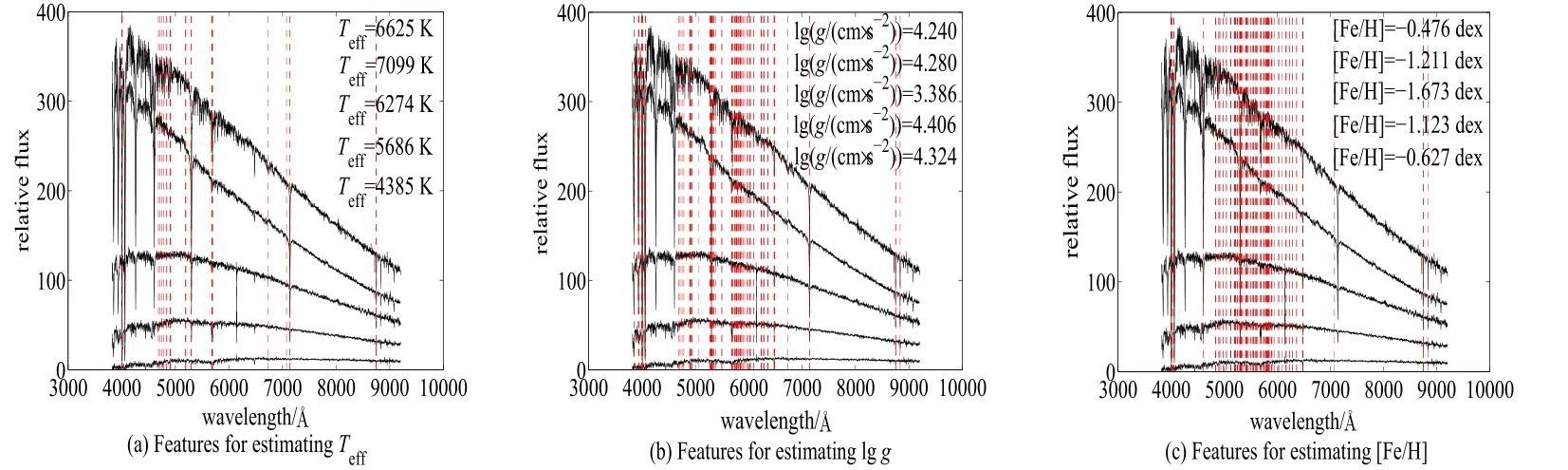
图1 为估计SDSS实测光谱的大气参数而检测到的特征.图中的曲线是具有不同参数的恒星光谱(右上角的参数与曲线从上到下依次对应).垂直虚线的横坐标就是特征的位置.Fig.1 Detected featu res for estim ating the atm ospheric param eters from SDSS stellar sp ectra.Cu rves are stellar spectra with d ifferen t param eters(the param eters in the upp er righ t corner correspond to the curves from top to bottom).The vertical dashed lines rep resent the w avelength positions of the detected featu res.

从表1中的多任务Lasso回归法的结果看,只是化学丰度([Fe/H])的结果相对好点,这可能是提取的特征数目多的缘故,而且其总共使用了4000条SDSS数据,其中75%的数据作为训练数据,而测试数据只用剩下的25%数据,有这样的结果也很正常,更不能表现出其方法的泛化能力强.而本实验使用了50000条SDSS数据,40%的数据作为训练集,60%的作为测试集,预测结果也很不错,足以说明本方案的泛化能力强,要比文献[15-16]的方法优越.

观察图1及表2,可以明显看出3个物理参量的被检测到的特征不仅数目不相同,而且波长位置不都一样,这充分体现出了多任务Sparse Group Lasso方法不仅可以提取到单个物理参量的光谱信息,还能够挖掘到不同物理参量之间的潜在关系信息.

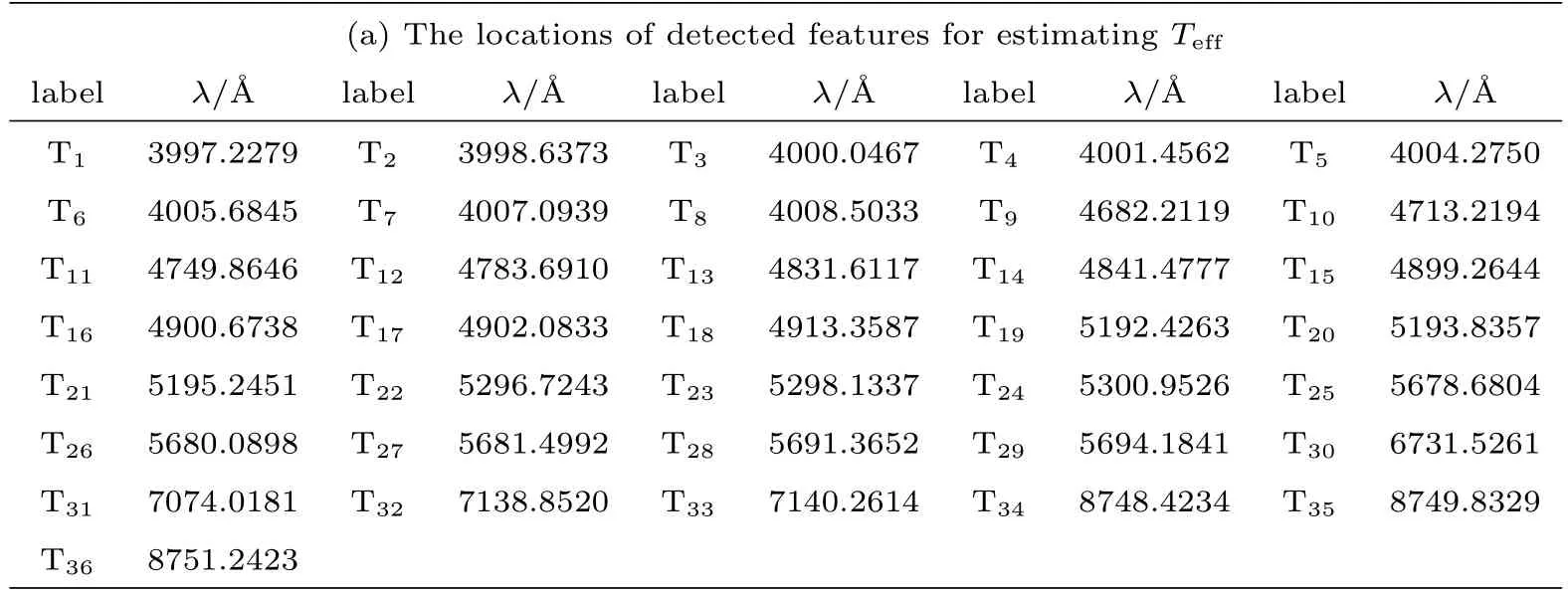
表2 SDSS实测光谱数据中检测到的特征及其波长位置Tab le 2 T he d etected featu res from SDSS sp ectra an d their w avelength p osition s

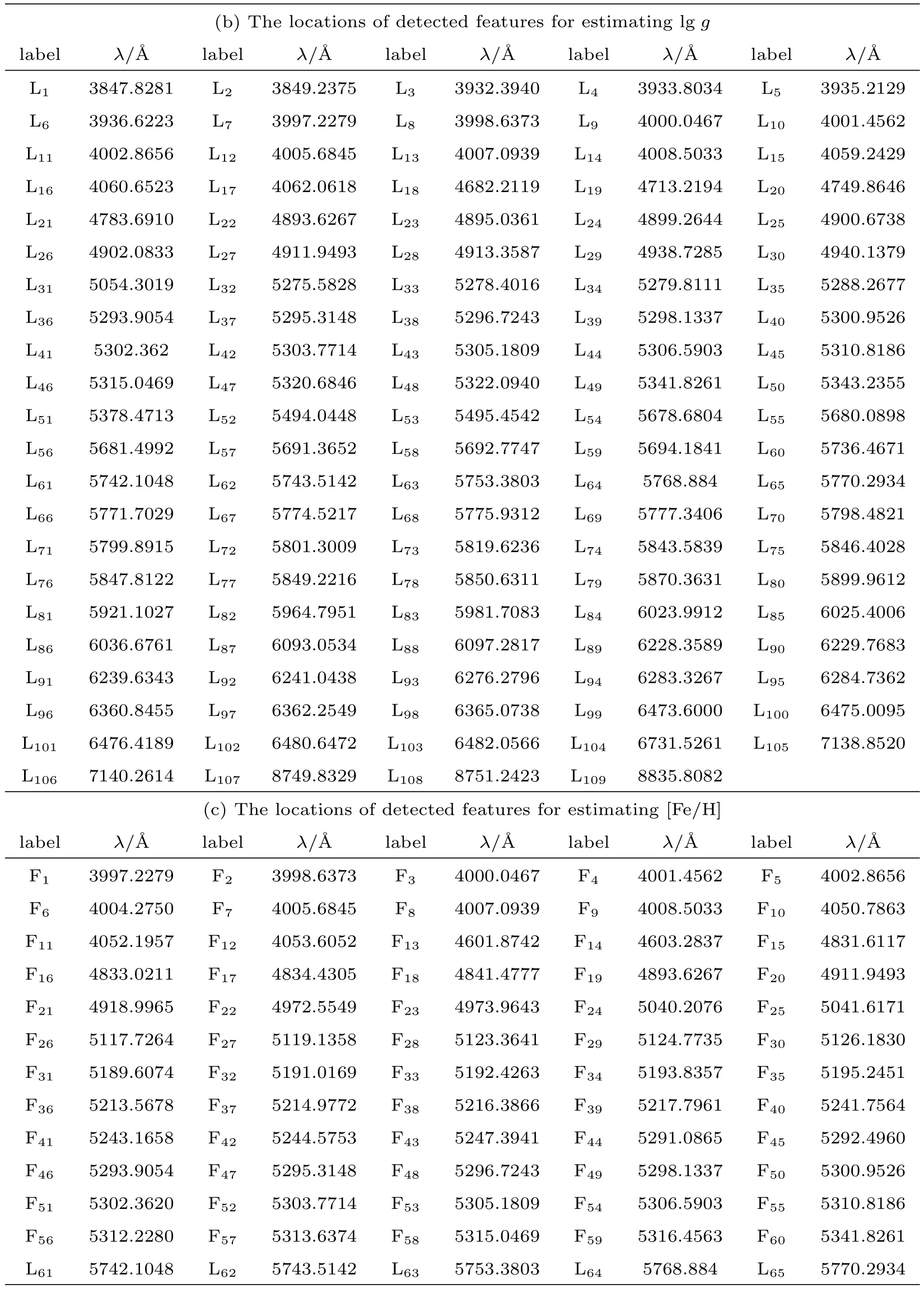
续表2Tab le 2 Con tinued

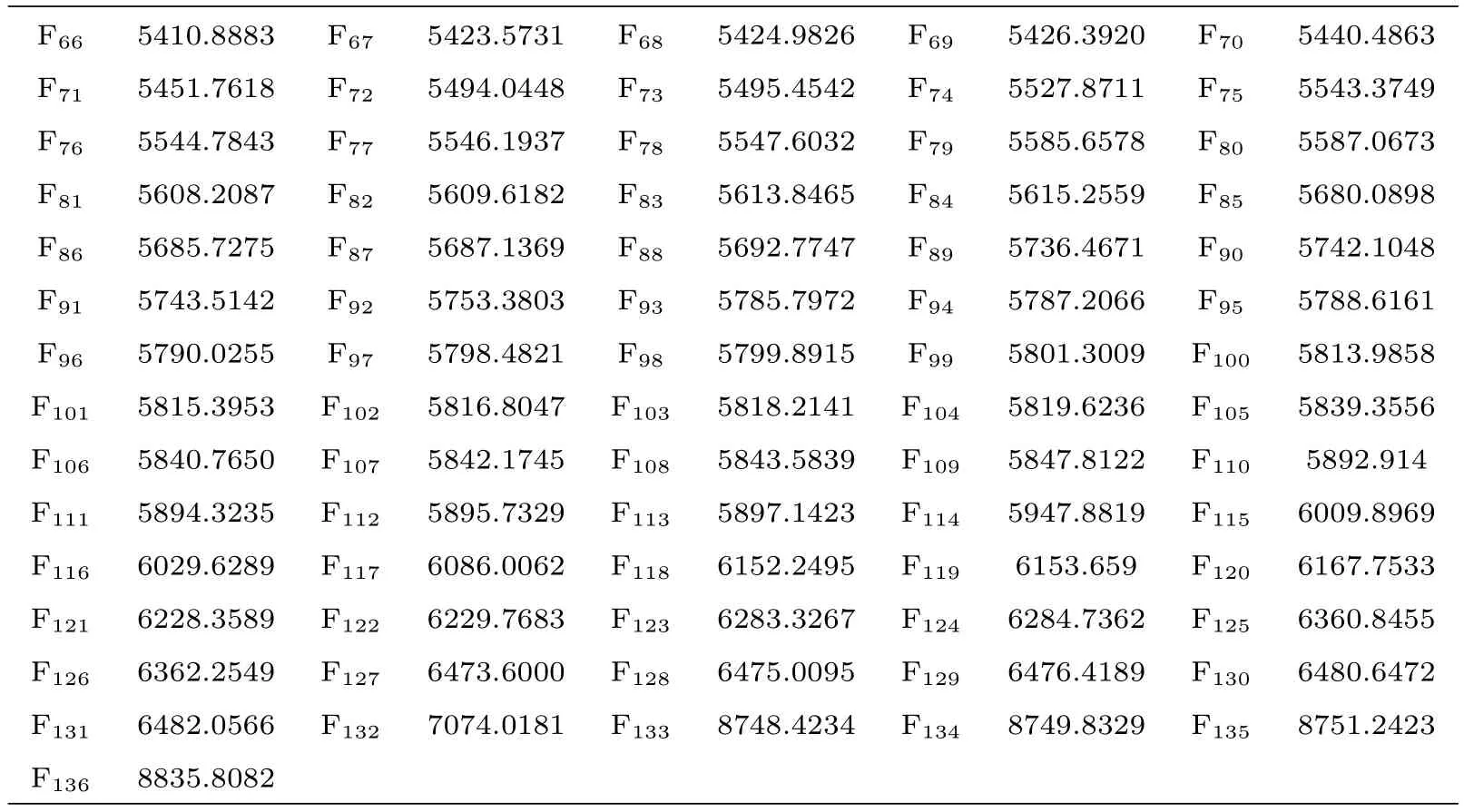
续表2Tab le 2 Con tinued

观察图2,可以看出3个参量误差的变化情况各不相同,但整体上误差都在0的附近变化,其中Teff的误差偏离最小,lg(g/(cm·s−2))的[1,2.8)、[Fe/H]的(−4,−2.2)dex区间误差偏离非常大,主要因为这些区间的光谱分布比较稀疏分散,其误差偏离度会随着训练数据的增多而改善[17].其次,Teff的整个区间误差精度都很高,而lg(g/(cm·s−2))的(3, 5)、[Fe/H]的(−2,1)dex区间误差精度稍高,其他区间的误差精度很低.另外,高估了巨星(lg(g/(cm·s−2))～2–3)的表面重力加速度,而低估了矮星(lg(g/(cm·s−2))～4)的表面重力加速度;高估了贫金属恒星([Fe/H]～−3–−2 dex)的化学丰度,而低估了太阳丰度恒星([Fe/H]～0 dex)的化学丰度.

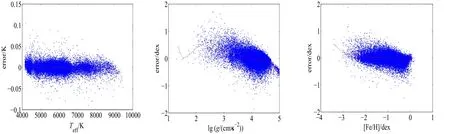
图2 在SDSS实测光谱上的估计误差对参数的相依性.横坐标是物理参量的真实值,纵坐标是参量的预测值与真实值的差.曲线是平均误差随参量变化的拟合曲线.Fig.2 The dep endency of estim ation error on the param eters to be estim ated on the SDSS sp ectra.T he horizontal axis is the true values of physical param eters,and the vertical axis is the d ifference between the estim ated va lues and the true values of the physica l param eters.T he cu rves are the fitting resu lts of the variation of the m ean error with the param eter.

5.2 理论光谱的结果与分析

在实验2中,同样有3个主要的操作步骤:首先对光谱数据进行预处理,然后用多任务Sparse Group Lasso提取光谱流量特征,最后用支持向量机回归(SVR)对光谱的3个物理参量进行估计.3个主要物理参量的平均绝对误差(MAE)、平均误差(ME)、标准偏差(SD),与一些相关文献方法的结果具体见表3.更重要的是分别检测出3个物理参量的特征:表面温度(Teff)21个、表面重力加速度(lg g)24个、化学丰度([Fe/H])24个,具体见图3及其具体位置见表4.另外,画出参量误差随Teff、lg g、[Fe/H]的变化情况,具体见图4.

表3 本文方法和文献中典型方案在理论光谱数据上的实验结果Tab le 3 Ex p erim en tal resu lts of the p rop osed m ethod an d som e ty p ica l schem es in the literatu re on the syn thetic sp ectra

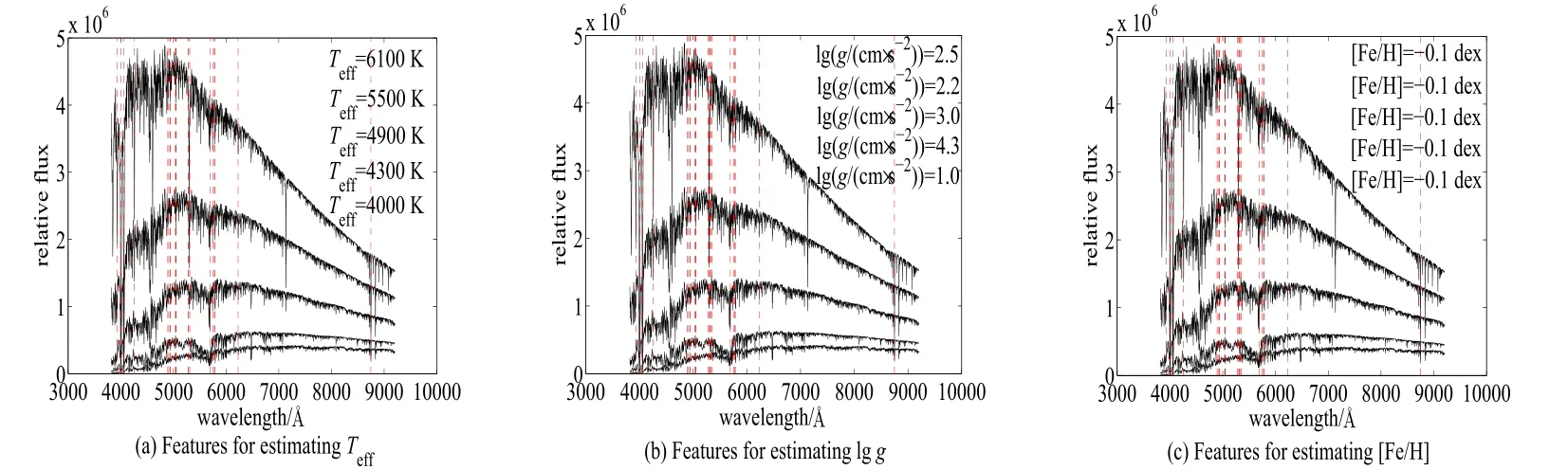
图3 为估计理论光谱的大气参数而检测到的特征.图中的曲线是具有不同参数的恒星光谱(右上角的参数与曲线从上到下依次对应).垂直虚线的横坐标就是特征的位置,与曲线交点的纵坐标就是被检测到的特征.Fig.3 Detected featu res for estim ating the atm ospheric param eters from syn thetic stellar sp ectra. Cu rves are stellar sp ectra with d ifferen t param eters(the param eters in the upp er right corner corresp ond to the cu rves from top to bottom).The horizon tal coord inates of vertical dashed lines rep resen t the w avelength positions of the detected featu res.The vertical coordinates of the intersections betw een the vertical dashed lines and the cu rves are the detected featu res.

观察表3,结合表1,可以看出本文采用的多任务Sparse Group Lasso特征提取与支持向量机回归(SVR)相结合的方案在理论光谱实验中预测效果比在实测光谱实验中预测效果更好.在表3中,不仅可以发现对表面温度(Teff)的预测最容易,化学丰度([Fe/H])次之,表面重力加速度(lg g)预测最难这个规律,还可以从平均绝对误差(MAE)看出本文方法预测结果的精度要比相关文献中非线性方法ANN及线性方法OLS高得多;平均误差(ME)都几乎为0也说明系统误差非常小;标准偏差(SD)很小也说明此方法对理论光谱物理参量的预测结果波动非常小.

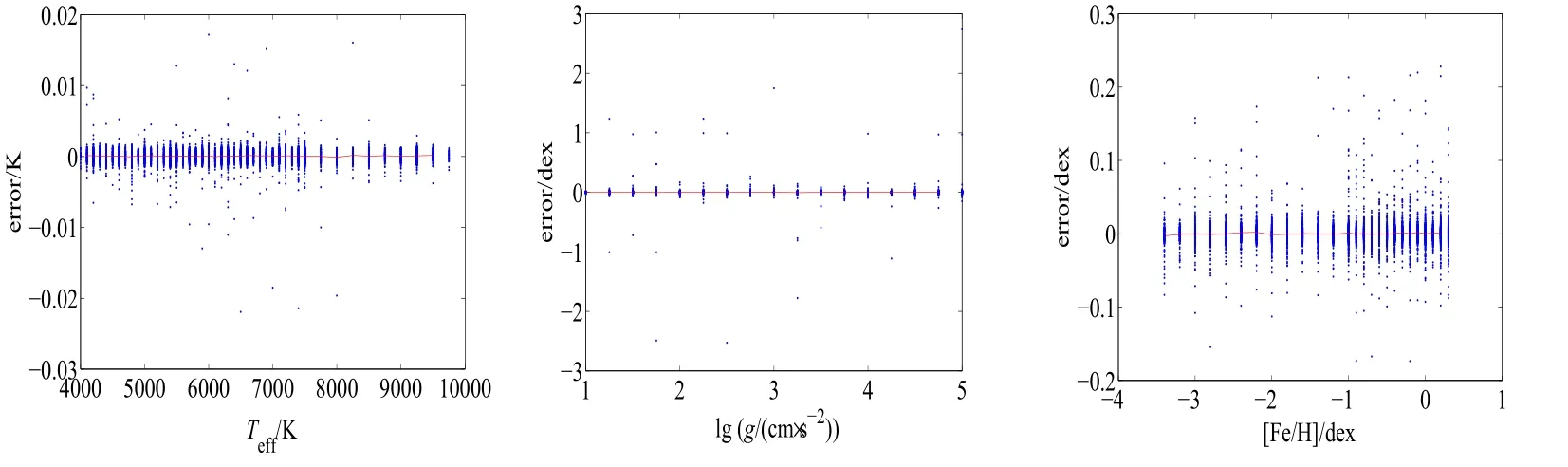
图4 在理论光谱上的估计误差对参数的相依性.横坐标是物理参量的真实值,纵坐标是参量的预测值与真实值的差.曲线是平均误差随参量变化的拟合曲线.Fig.4 The dependency of estim ation error on the param eters to be estim ated on the synthetic spectra. T he horizonta l ax is is the true va lues of physica l param eters,and the vertica l ax is is the error betw een the estim ated va lues and the true values of the physica l param eters.T he cu rves are the fitting resu lts of the variation of the m ean error with the param eter.

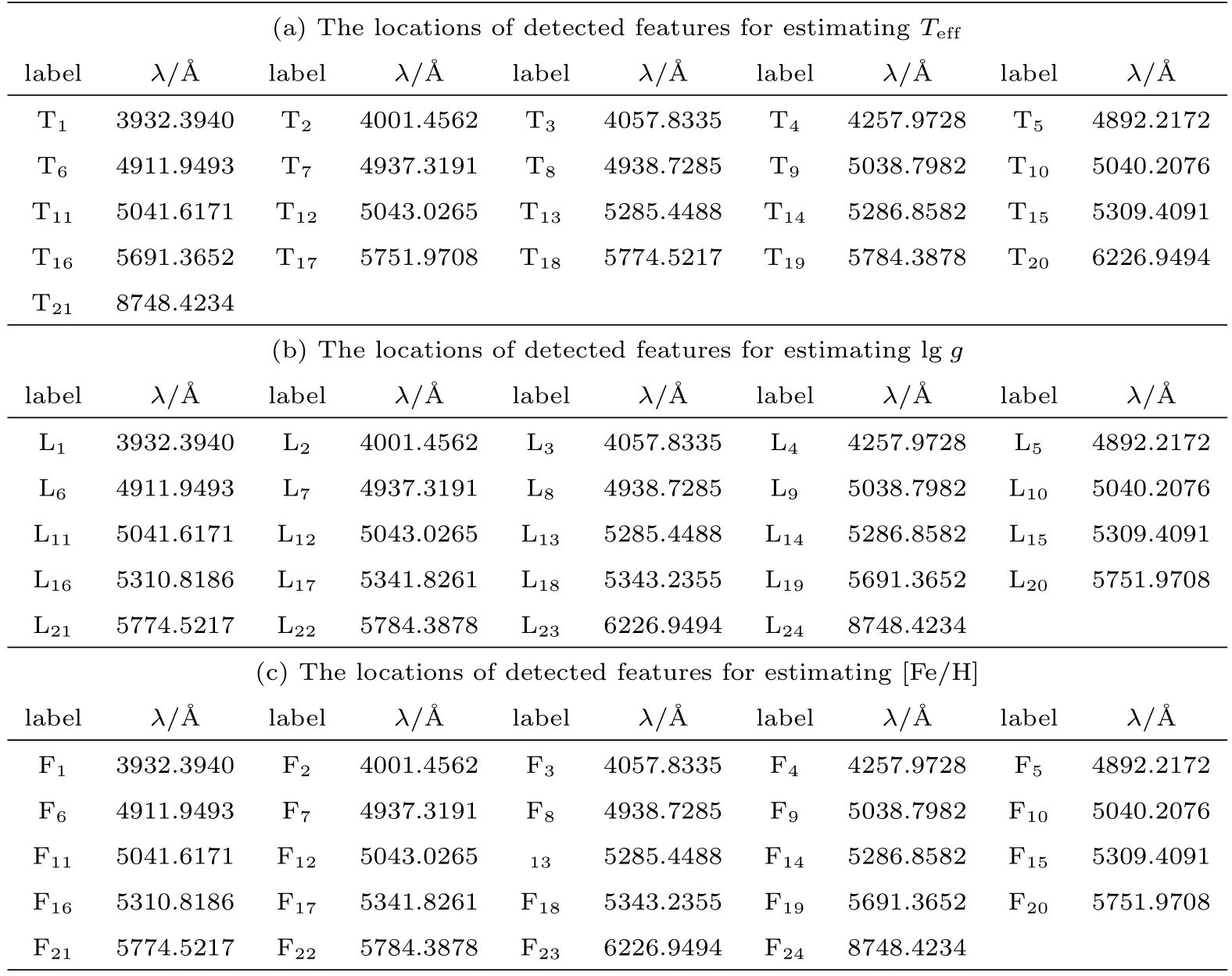
表4 从理论光谱数据中检测到的特征及其波长位置Tab le 4 T he detected featu res from syn thetic sp ectra and their w avelength p ositions

查看图3及表4,可以看到在理论光谱数据上检测到3个物理参量的特征数目不仅很接近而且明显要比实测光谱的少;表面温度(Teff)的特征与另外2个物理参量的特征位置很相近,甚至表面重力加速度(lg g)与化学丰度([Fe/H])的特征位置完全一样,这很可能是由Kurucz的NEWODF模型得到的理论光谱数据,没有各种噪声干扰的缘故.

观察图4,可以看出3个参量误差的变化情况大致相同,呈沿着纵轴0值的一条直线, Teff、lg g、[Fe/H]的区间误差偏离都非常小且误差精度都很高,这是由于理论光谱训练数据在整个参数范围内比较集中且分布均匀.

6 总结与展望

本文把对3个重要的光谱物理参量表面温度(Teff)、表面重力加速度(lg g)、化学丰度[Fe/H]的估计,作为3个任务,用多任务Sparse Group Lasso提取特征,然后再用支持向量机回归(SVR),不仅估计的结果精度高、鲁棒性好、泛化性能高,而且操作简单、计算速度快.同时,这种对大数据多任务学习的方式,不仅学习到了单个任务的信息,而且兼顾学习到了多个任务之间的关联信息.总的来说,本文采用的多任务Sparse Group Lasso特征提取与支持向量机回归(SVR)相结合的方案对恒星大气物理参量的估计结果要优于相关文献中方法的结果.另外此方案不仅适用于多任务光谱数据的处理,还适用于其他类型大数据的多任务学习,比如银行金融大数据,期货股票大数据,淘宝交易大数据等等.

当然,在SDSS实测光谱数据上,对于本文多任务Sparse Group Lasso所提取光谱特征的数目可以探讨进一步减少,同时保证估计的准确度.比如说可以做探索性实验,使用多任务Sparse Group Lasso提取特征之后,然后使用主成分分析(PCA)再次剔除冗余噪声或者采用对提取的每个光谱特征的邻近区域的一些特征求均值,以达到特征数目的减少,可以深入做实验以检验经过这些方式处理后的估计值精度是否有所提高等等.

致谢衷心感谢潘儒扬在论文修订、校对中提供的帮助.

[1]Ahn C P,A lexand roff R,A llende P rieto C A,et a l.A p JS,2012,203:21

[2]Cu i X Q,Zhao Y H,Chu Y Q,et a l.RAA,2012,12:1197

[3]Fioren tin P R,Bailer-Jones C A L,Lee Y S,et al.A&A,2007,467:1373

[4]李乡儒.天文学进展,2012,30:94

[5]T ibsh irani R.Jou rna l of the Roya l Statistica l Society Series B,1996,58:267

[6]Li X R,W u Q M J,Luo A L,et a l.A p J,2014,790:105

[7]Sim on N,Friedm an J,Hastie T,et a l.Jou rnal of Com pu tational&G raph ica l Statistics,2013,22:231

[8]Liu J,Ji S,Ye J.P roceed ings of the Tw enty-fifth Con ference on Uncertain ty in A rtificia l In telligence, 2009:339

[9]V incen t M,Hansen N R.Com pu tationa l Statistics&Data A nalysis,2014,71:771

[10]Liu J,Ye J.A dvances in Neu ral In form ation P rocessing System s,2010,23:1459

[11]张吐辉,张海.纯粹数学与应用数学,2014,30:178

[12]Yuan M,L in Y.Jou rna l of the Roya l Statistical Society Series B,2006,68:49

[13]Jofr´e P,Panter B,Hansen C J,et al.A&A,2010,517:57

[14]谭鑫,潘景昌,王杰,等.光谱学与光谱分析,2013,33:1397

[15]常丽娜,张培爱.天文学报,2015,56:26

[16]Chang L N,Zhang P A.ChA&A,2015,39:319

[17]Lu Y,Li X R.M NRAS,2015,452:1394

A pp lication of M u lti-task Sparse G roup Lassofeatu re Ex traction and Support Vector M achine Regression in the Stellar A tm ospheric Param etrization

GAO Wei LIXiang-ru

(Schoo l of M a them a tica l Scien ces,Sou th China Norm a l Un iversity,G uangzhou 510631)

Themulti-task learning puts themultiple tasks together to analyse and calculate for discovering the correlation between them,which can im prove the accuracy of analysis resu lts.This kind of methods have been w idely studied in machine learning,pattern recognition,com puter vision,and other related fields.This paper investigates the app lication ofmu lti-task learning in estimating the effective tem perature(Teff),surface gravity(lg g),and chem icalabundance([Fe/H]).Firstly,the spectral characteristics of the three atmospheric physical parameters are extracted by using the multi-task Sparse Group Lasso algorithm,and then the support vectormachine is used to estimate the atm ospheric physical param eters.The proposed schem e is evaluated on both Sloan stellar spectra and theoretical spectra computed from Kurucz’s New Opacity Distribution Function(NEWODF)model.Them ean absolute errors(MAEs) on the Sloan spectra are:0.0064 for lg(Teff/K),0.1622 for lg(g/(cm·s−2)),and 0.1221 dex for[Fe/H];The MAEs on synthetic spectra are 0.0006 for lg(Teff/K),0.0098 for lg (g/(cm·s−2)),and 0.0082 dex for[Fe/H].Experimental results show that the proposed schem e is excellent for atm ospheric parameter estim ation.

stars:fundamental parameters,methods:data analysis,methods:statistical,methods:m iscellaneous

P144;

A

10.15940/j.cnki.0001-5245.2016.04.002

2015-12-10收到原稿,2016-01-26收到修改稿

∗国家自然科学基金项目(61273248,61075033)、国家自然科学基金委员会-中国科学院天文联合基金项目(U1531242)和广东省自然科学基金项目(2014A030313425,S2011010003348)资助

†xiangru.li@gm ail.com