天体测量法探测系外行星∗

许伟维 廖新浩 周永宏 许雪晴

(1中国科学院上海天文台 上海 200030) (2上海科技大学物质学院 上海 201210) (3中国科学院行星科学重点实验室 上海 200030) (4中国科学院大学 北京 100049)

天体测量法探测系外行星∗

许伟维1,2,3,4†廖新浩1,3‡周永宏1,3许雪晴1,3

(1中国科学院上海天文台 上海 200030) (2上海科技大学物质学院 上海 201210) (3中国科学院行星科学重点实验室 上海 200030) (4中国科学院大学 北京 100049)

在目前已发现的系外行星中,绝大多数是由视向速度法和凌星法探测得到的,天体测量法仅发现了1颗.gaia卫星数据即将发布,天体测量法将逐步成为系外行星探测的重要方法之一.基于天体测量法给出的恒星位置参数序列,讨论了在求解行星质量和轨道参数时涉及的动力学条件方程计算问题,给出了具体微分改正公式,同时也进行了必要的仿真模拟计算.建立的方法可以较容易地推广到多行星系统.

系外行星,天体测量学,天体力学:轨道计算与定轨,方法:数据分析

1 引言

系外行星探测和研究是当今国际天文学研究的热点.1995年,M ayor和Queloz采用视向速度法在飞马座51附近发现了第1颗围绕着主序恒星运动的木星质量量级的系外行星飞马座51 b[1].近年来,随着天文探测技术的进步,特别是Kep ler空间望远镜的成功发射和观测,新的系外行星不断被发现,其数量明显增多.根据系外行星网站(exop lanets.eu)统计,截止2015年12月1日,已确认发现2004颗系外行星,隶属于1269个行星系统,包括498个多行星系统;此外,400多颗系外行星候选体需进一步认证.在这些已发现的系外行星中,绝大多数为气态巨行星和热木星(约占70%),部分为超级地球(20%)和地球质量大小的行星(2%),但尚未确认存在生命的类地行星系统.

系外行星的探测方法分为间接探测和直接成像,间接探测有视向速度法、天体测量法、脉冲星计时法、凌星法、微引力透镜法等[2],目前实际观测中采用最多的是视向速度法和凌星法.天体测量法至今只发现了一颗系外行星—HD 176051 b[3].2009年以前,由于HARPS(High Accuracy Radial velocity Planet Searcher)的应用[4],视向速度法为主要的探测方法;2009年美国国家航空航天局(National Aeronautics and Space Adm inistration,NASA)建造的开普勒太空望远镜发射升空,凌星法逐渐成为主流方法,目前该方法已发现超过1200颗系外行星(exop lanets.eu).2013年12月19日,欧洲空间局(European Space Agency,ESA)研制的gaia空间望远镜升空,其目的是以前所未有的精度对银河系内数以十亿计的恒星进行观测,测量他们的位置、距离和运动,其观测效率将比同样由ESA发射的依巴谷卫星高出数百万倍[5].因此,人们对于利用gaia开展太阳系与系外行星的探测寄予厚望.

天体测量法是通过测量恒星空间位置变化来反演其附近行星的质量和轨道参数的,相比于目前通常采用的视向速度法和凌星法,天体测量法有其独特的优势:(1)直接确定行星质量.视向速度法也是通过测量恒星空间位置变化来反演其附近行星的轨道参数的,但因其观测方程中仅包含了行星质量m与行星轨道倾角的正弦sin i的乘积项,所以只能推算出m sin i,不能直接确定行星的质量.天体测量法对应的观测方程不仅包含了m cos i项,而且包含m项,故可以通过观测资料同时直接推算出行星的质量与轨道倾角[6].(2)寻找长周期行星.根据开普勒第三定律可知,行星绕恒星运动的轨道半长径3次幂与行星轨道周期的平方成正比;同样质量的行星,行星轨道半长径越长,对于恒星绕系统质心运动的扰动就越大,因此越容易被天体测量法分辨出来.所以天体测量法对长周期行星探测较为敏感.(3)检测多星系统是否共面.在已知的系外行星中,大多数具有较大的轨道偏心率,其原因可能是由于受到一颗或多颗大质量天体的引力作用[7],该作用力使得行星的轨道面不与恒星的赤道面共面,若在多星系统中,该作用力将使得各行星轨道不共面[8].研究行星质量和相互夹角对于多星系统的动力学模型、动力学稳定以及轨道共振具有重要意义.(4)太阳系附近寻找类地行星.利用空间干涉的天体测量能达到亚微角秒级的精度,对于造成恒星扰动的行星质量检测可达到m⊕(地球质量)量级,满足在太阳系附近寻找类地行星的要求[9].

对于由1颗恒星和1颗行星组成的二体系外行星系统,W right和Howard于2009年建立了基于轨道根数的天体测量法对应的观测方程[10],其在赤道坐标系下,包含了视差、自行以及行星质量和轨道根数等参数.通过分析二体运动的解和参数估计理论,可以给出这些参数的最优解.稍加分析即可发现,基于轨道根数的天体测量方法,当行星轨道偏心率e=0时,因状态转移矩阵奇异而失效,特别是对于多行星系统,基于轨道根数的状态方程和状态转移矩阵计算都非常复杂,不便于实际应用,因此需要建立简洁可行的确定系外行星轨道的天体测量方法.本文针对多体系统动力学特性,提出采用坐标速度描述,不仅可以避免e=0对应的状态转移矩阵奇异问题,而且可以显著降低整个计算的复杂性.本文第2节对gaia测量数据用于系外行星的确定进行了必要的精度分析;第3节较全面地总结了基于轨道根数的天体测量方法涉及的理论基础;第4节给出了基于坐标速度的天体测量方法对应的观测方程、运动方程和状态转移方程;第5节列出了仿真模拟计算结果并作了一些分析;第6节推导了行星轨道确定时初始估计满足的约束条件,由此可以显著提高轨道确定微分改正的收敛效率;第7节推导了三体问题(1颗恒星2颗行星)的计算公式;最后1节给出本文的结论,同时也讨论存在的问题及其解决途径.

2 天体测量观测精度分析

当恒星附近存在行星时,由于引力作用,使得恒星与行星绕着它们的质心以相同的角速度作椭圆运动.假设恒星和行星围绕系统质心运动轨道半长径分别为as和ap,则在地面上观察恒星轨道半长径时,可产生一个角度2θ[11](如图1).

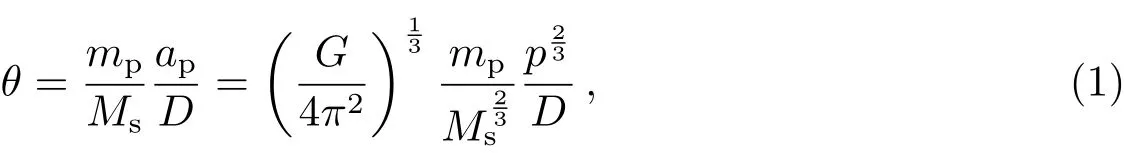
其中,Ms和mp分别为恒星和行星的质量,G为万有引力常数,D为恒星与观测者之间的距离,p为二体运动的轨道周期.角半径θ也称作恒星的天体测量特征角,表征了行星对恒星的扰动大小,除行星质量外,还与恒星的质量、轨道周期及观测距离有关.根据目前已发现的系外行星,表1列出了它们的质量与轨道周期分布范围,以及所绕恒星的质量和与观测距离的分布范围(参见网站exop lanets.eu),其中行星质量单位为MJ(木星质量),恒星质量单位为M⊙(太阳质量).针对上述参数分布范围,本文选取了5种模型,模型中恒星质量皆取为1 M⊙,行星质量、轨道周期以及观测距离不等,计算5种模型中恒星的天体测量特征角,见表2.

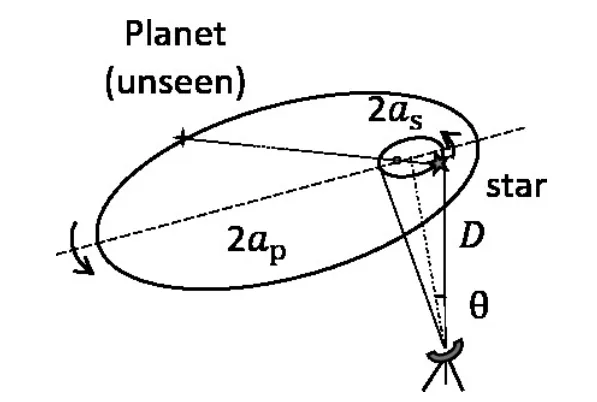
图1 二体运动的轨道示意图Fig.1 The orbita l sketch of the tw o-body m otion

表1 已知系外行星的部分参数范围Tab le 1 The partial param eters’range of the know n exop lanets

表2 几种模型下恒星天体测量特征角Tab le 2 The astrom etric signatu re of the star in d ifferen t m odels

由于gaia对于不同星等的恒星观测精度不同,所以还需分析gaia对于系外行星的可观测性.表3给出了对于太阳质量级的恒星,当其观测距离在1000 pc内时的星等及gaia对应的位置测量精度,由表可知:在1000 pc内,恒星的视星等mV=14.75mag,gaia的观测精度高于10µas,其值均小于表2中各模型的天体测量特征角,因此gaia可进行有效观测.

表3 太阳质量级恒星在不同距离的视星等及gaia对其的观测精度Tab le 3 The ap paren t m agn itude of the sun like stars at d ifferen t d istances and the accu racies of the gaia

3 基于轨道根数的观测方程

利用天体测量法间接探测系外行星时,通过观测恒星的周期性位置变化来判断其是否存在.对于1颗孤立的恒星,可通过5个天体测量观测值来描述其在天球上的角位置,分别是赤道坐标系下的赤经α0、赤纬δ0(在某一特定的坐标系下某一历元时的值,现在一般都取在国际天球参考系下J2000.0的值),恒星自行相应的正交分量µα、µδ,以及视差ϖ;绕着恒星作椭圆运动的行星轨道可由6个轨道根数描述,即轨道半长径a、倾角i、升交点经度Ω、近星点经度ω、偏心率e及平近点角M;行星质量m可由p和a通过Kep ler第三定律确定.因此,对一个含有n颗行星的系统进行轨道拟合时,需要5+7n个参数.

建立如图2所示观测示意图,恒星的运动轨道处于O-X YZ坐标系内,O-xyz系为观测面所在坐标系,z轴表示观测者视线方向,x轴指向北极,y方向由右手法则确定,i、Ω、ω为3个方位角.

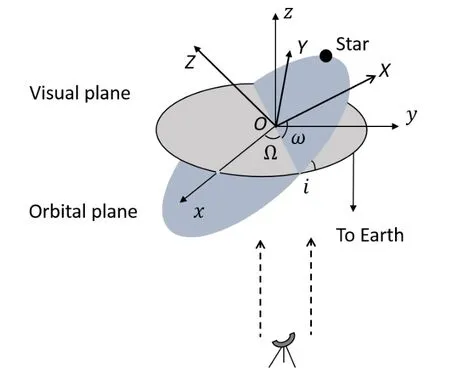
图2 二体运动的观测示意图Fig.2 T he sketch of the observation of the tw o-body m otion

恒星在空间位置的变化反映了其椭圆轨道运动在观测面上的投影,由赤经和赤纬两个位置参数决定,分别用ˆη(t)、ˆξ(t)表示,对应的观测方程为

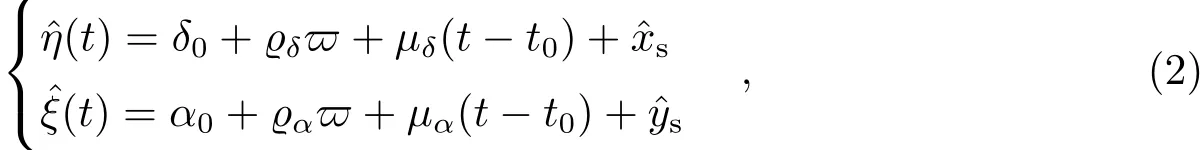
等式左边为观测值,右边各项依次为初始值、视差改正、自行改正以及天体扰动项,其中,ϱα、ϱδ表示视差改正参数;ˆxs、ˆys表示恒星运动在观测面上两个方向的投影,单位为角度;为了计算和公式表达的方便,选取适当的计算单位是必要的,本文分别采取太阳质量M⊙、太阳赤道半径A⊙作为基本质量和长度单位,取引力常数G=1,则相应的时间单位为

故可通过观测距离D将ˆxs、ˆys归算到系统长度单位下,分别用xs、ys表示

考虑恒星附近仅存在1颗行星情况,即n=1,由天体力学二体问题分析解可将xs、ys表示为

其中,

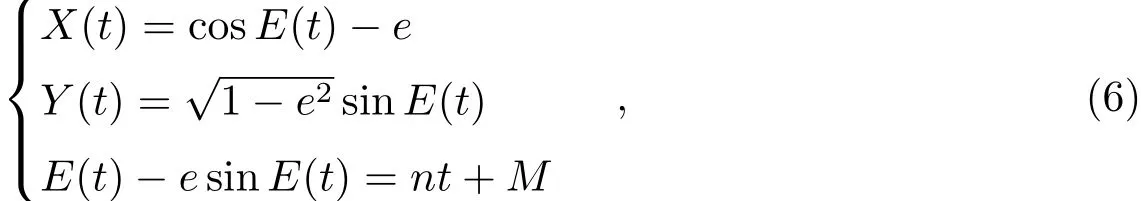
A、B、F、G称为Thiele-Innes常数[13],可由轨道根数描述,

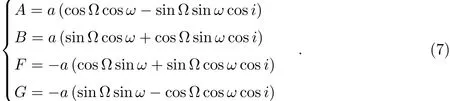
恒星视差与自行改正可通过一定量天体测量数据计算出来,故在后面的计算中将视差与自行视为已知量.至此,我们可将观测方程改写为

这里,η′(t)和ξ′(t)包含了自行和视差改正项,已归算为系统长度单位.假设初始时刻恒星轨道根数和行星质量的估计值为a∗、i∗、Ω∗、ω∗、e∗、M∗及m∗,为方便起见,用矢量将其表示为σ=(σ1,σ2,σ3,σ4,σ5,σ6,σ7).对上式在恒星初始运动位置处展开,有:

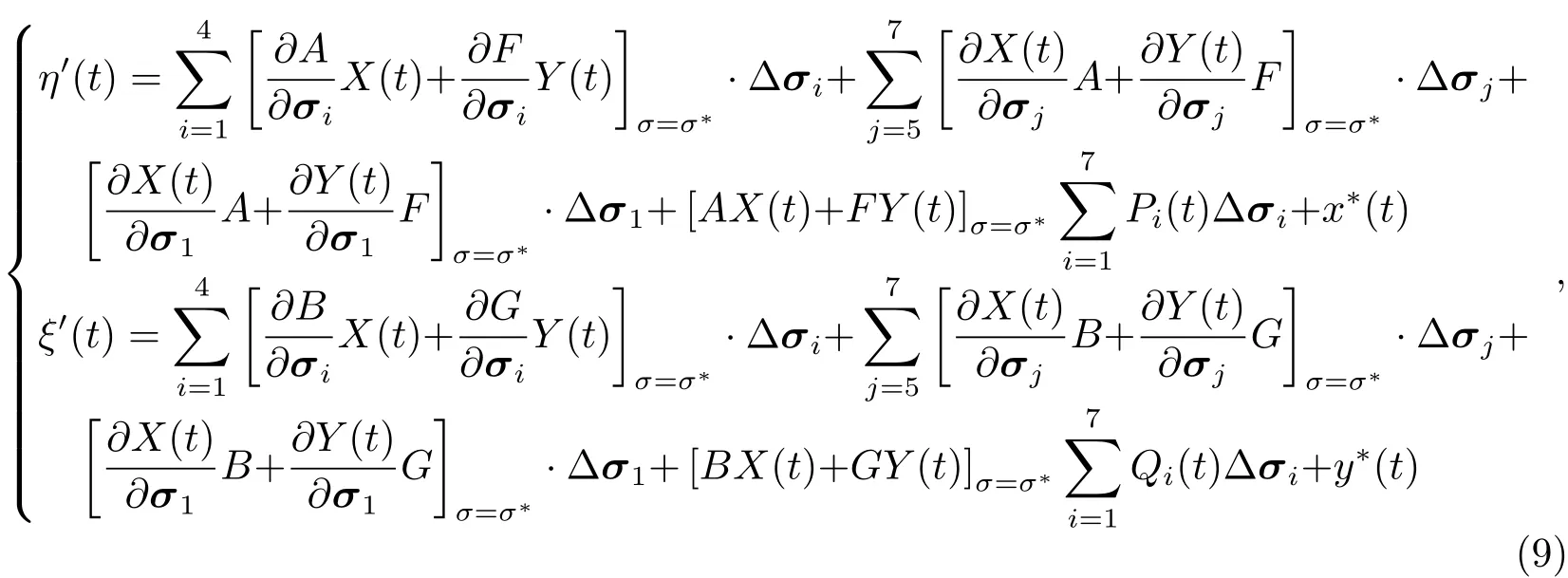
其中,Pi(t)、Qi(t)依次表示对7个参数的微分结果.如果有k次观测,那么2k个观测方程可以写成矩阵形式

其中,

上述方程(10)包含7个未知量,因此问题可解至少需要观测4次.

将由估计理论首次解得的∆σ(0)叠加到初始时刻近似轨道上,进行迭代计算,当第l次迭代给出的|∆σ(l)|小于设定的收敛标准ε时,求解完成.本文统一设定误差限ε= 10−6.

由上述获得的恒星轨道根数与行星质量的估计值,可以求出恒星初始时刻的坐标→rs与速度˙→rs,由此根据二体关系式,可以求出行星此时对应的坐标→rp与速度˙→rp,

对于多行星系统,即n≥2,对应的运动没有分析解,故上述方法不再适用.

4 基于坐标速度的观测方程

观测方程与轨道根数法对应的恒星观测方程相同,即(2)式.假定t=t0时刻恒星位置与速度和行星质量的估计值分别为(t0)、(t0)、mp,其近似值(即初始估计)为、、m∗,两者相差为∆、∆、∆m,将观测方程在、、m∗处展开有

当t=t0时,状态转移方程涉及的初始条件为

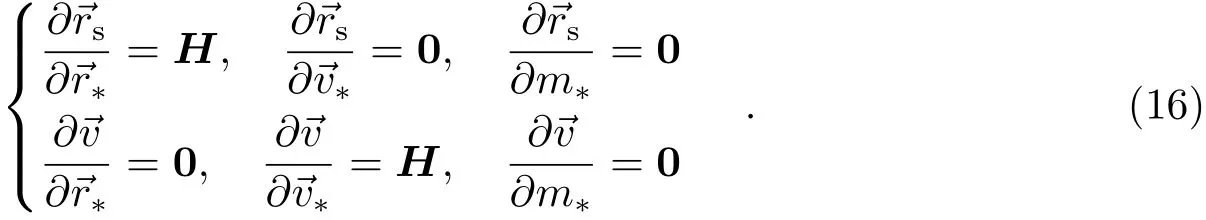
这里,H为3阶单位矩阵.

5 轨道特征分析与仿真计算

目前,gaia的巡天数据仍未释放,因此为了验证上述方法的有效性,只能进行仿真模拟计算.假定t0时刻1组恒星的轨道根数和行星质量σ(t0),由该组参数可模拟出1组恒星位置的观测数据,然后用其反解σ(t0),由此可以验证和分析评估轨道确定的方法和精度.

5.1 轨道特征的影响

5.1.1 小偏心率

对于小偏心率轨道,轨道根数法不能进行轨道确定,但坐标速度法仍有效,其原因是e=0时近星点经度不能确定所致.具体体现在当e=0时,xs、ys可表示为:

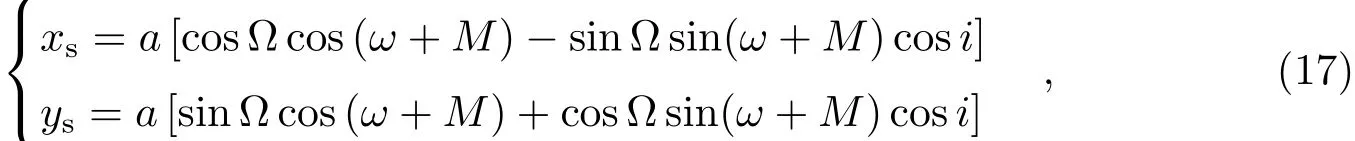
由上式可以看出

即状态转移矩阵中有关ω和M的两列相关,导致状态转移矩阵奇异,故对于小偏心率的情况,轨道根数法失效.

5.1.2 轨道倾角

对于倾角i=0°或180°的轨道,两种方法都不适用.

轨道根数法中,由于xs、ys中包含的i项都以cos i出现,故当i=0°或180°时,xs、ys对i的偏导数都为0,具体体现在

坐标速度法中,当i=0°时,中不显含z分量,即z∗和分量.故有

两种情况都导致线性方程组的系数矩阵奇异,无唯一解.

此外,天体测量法描述的是恒星X、Y方向的运动在观测面上的投影,对于Z方向没有直接约束,这就造成了当i↔π−i时,σ(t0)一样能满足观测方程.但此时除倾角项外,升交点的经度Ω和近地点的经度ω也存在相应的变化,这一点我们可从Thiele-Innes常数来理解.我们将其对应关系整理如下:

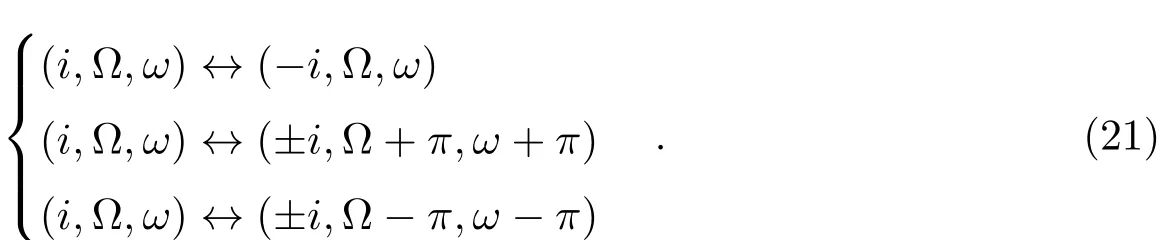
5.2 观测误差的影响

观测即有误差,因此不同的仿真模型应增加相应的观测误差.以第2节中模型A为例,mV=5.63mag＜10mag,此时gaia的观测精度∆θ=4µas,若将其视为天体测量观测误差,对于观测距离D=15 pc,该误差s的大小为

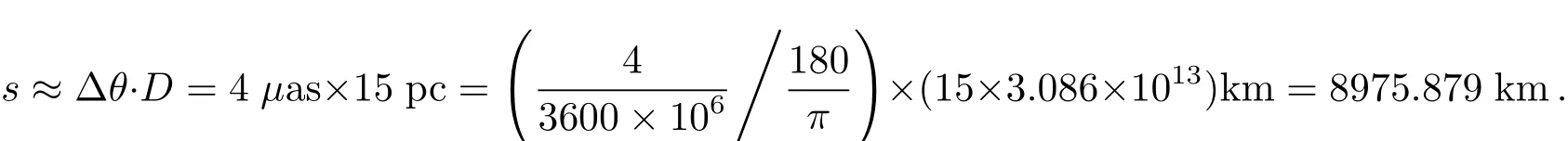
将其归算到系统长度单位A⊙,即得该模型的观测误差∆s为

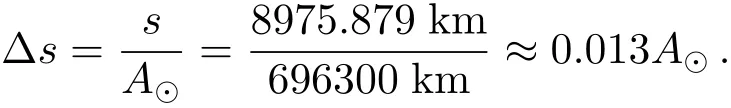
通过M atlab软件可计算出任意两组满足均值为0、方差为0.013的高斯白噪声,将其分别增加到恒星的x和y方向的观测数据上,则可获得含有观测误差的模拟观测数据.

由含有误差观测数据可确定初始根数σ(t0)的估计值¯σ(t0),两者之差为∆σ.表4列出了几种模型对于不同观测误差和不同观测次数时确定的初始轨道估计值误差情况.模型A表示一个轨道周期为2 yr的木星绕一个距离地球15 pc的太阳作椭圆运动(见表2),此太阳在天球上位置变化最大角度(特征角)为100µas,考虑不同观测误差与观测次数的组合,形成了3组模拟观测数据:A-1、A-2和A-3.模型A的初始轨道根数取为:a=1.587 au,e=0.4000,i=40.00°,Ω=80.00°,ω=50.00°,M=50.00°, m=9.552×10−4Ms;轨道确定误差统计分为x、y方向的残差及轨道根数的相对误差.以A模型为例,对于特征角为100µas的系外行星系统,考虑观测随机误差分别为2µas和4µas以及观测点数分别为20和40的情况.模型A-1对应观测误差2µas,观测点数20,由坐标速度法确定的轨道残差的x和y分量分别为23.75µas和24.20µas,由轨道根数法确定的轨道半长径和轨道偏心率的相对误差分别为1.65%和0.92%,其他根数的误差均小于10%,质量确定的精度较高,可好于千分之一;模型A-2对应观测误差2µas,观测点数40,相较于A-1各根数的相对误差均显著减小,即拟合结果更优;模型A-3对应观测误差4µas,观测点数40,相较于A-2大部分根数的相对误差有所增大.通过比较不同模型对应的计算结果表明,观测数据越多,相对误差越小,轨道确定的拟合结果越可靠.

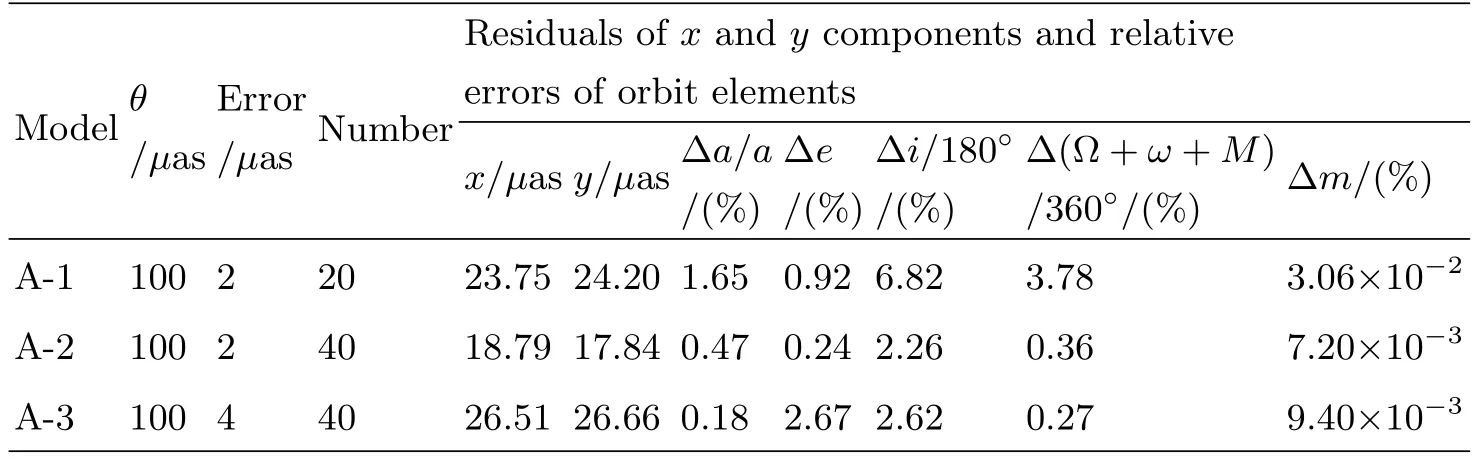
表4 模型A-1、A-2和A-3的计算结果Tab le 4 T he ca lcu lation s of the m od els A-1,A-2,an d A-3

5.3 初值的选取

由于观测方程(2)中关于恒星初始轨道根数或恒星初始坐标速度函数的表示均是非线性的,故在轨道确定中需要采用微分迭代方法求解轨道估计值,因此需要选定恰当的迭代初值,以使求解过程收敛.对于轨道初值的选取,最简单的方法是在一定区间内对每个待解参数进行扫描计算,当迭代初值被选取在参数收敛区间时,便可给出估计值.本文讨论的问题涉及的参数收敛区间是7维的,因此要获得收敛的估计值,需要较大的扫描计算量.为了方便计算,采用固定Ω、ω、M、m进行a、i、e 3维检索,再固定a、i、e、m进行Ω、ω、M 3维检索.计算结果列于表5,表中列出的是相对误差百分比值,需要说明的是其中角度量的误差相对量取180,偏心率的误差相对量取为1,主要是为了避免小偏心率作为相对量导致相对误差失真.模型A-1和A-3的轨道半长径收敛区间约为5%,其他根数的收敛区间相对较大,一般大于10%,有些甚至可达20%.从初步的扫描计算结果看,轨道半长径a的迭代初值选取是影响计算收敛与否的关键因素,需要尽量靠近估计值.

表5 模型A-1和A-3的收敛区间Tab le 5 The convergen ce in terval of the m od els A-1 and A-3

6 关于初始估计取值的约束

在上节讨论中,为减少计算时间,对7维参数空间仅进行了两个3维参数空间扫描,且行星质量均是固定的,没有参与扫描计算.事实上,可通过恒星空间位置观测资料时间序列对上述7维参数空间进行适当的约束,降低参数空间的维数.具体做法如下:已知由天体测量方法给出的某颗恒星的位置时间序列xs(tj),ys(tj),j=1,2,···,k,其包含了运动周期信息,通过对其傅里叶谱分析(FFT)可获得轨道周期p,再根据开普勒第三定律可以给出恒星轨道半长径a和行星质量mp之间的关系式,

一般认为Ms的值可由天体物理方法获得.

傅里叶谱分析通常针对等间距数据(均匀采样)进行,故需要先对恒星的观测数据进行插值,再利用插值数据进行谱分析.此外,还采用了另一种方法——LSQ(最小二乘拟合),将插值后的数据进行最小二乘,拟合成一条正弦曲线,该正弦曲线的周期即为恒星运动周期.

已知gaia的观测年限为5 yr,故进行傅里叶谱分析所选取的模型周期不应该大于5 yr,否则无法观测到一个完整周期的数据;又根据奈奎斯特取样定理,所选模型周期应限制在2.5 yr内.此处,我们选取5.2节中所建立的模型进行计算,图3给出了A-3模型(任意选取)x、y方向误差数据的分布及进行傅里叶分析的结果,并将计算结果列于表6中.

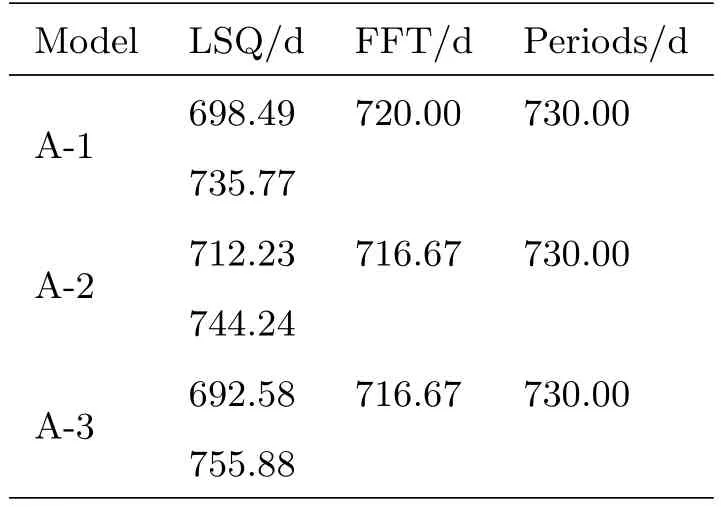
表6 模型A-1、A-2、A-3进行最小二乘拟合和傅里叶分析的结果Tab le 6 T he LSQ an d FFT resu lts of the m od els A-1,A-2,and A-3

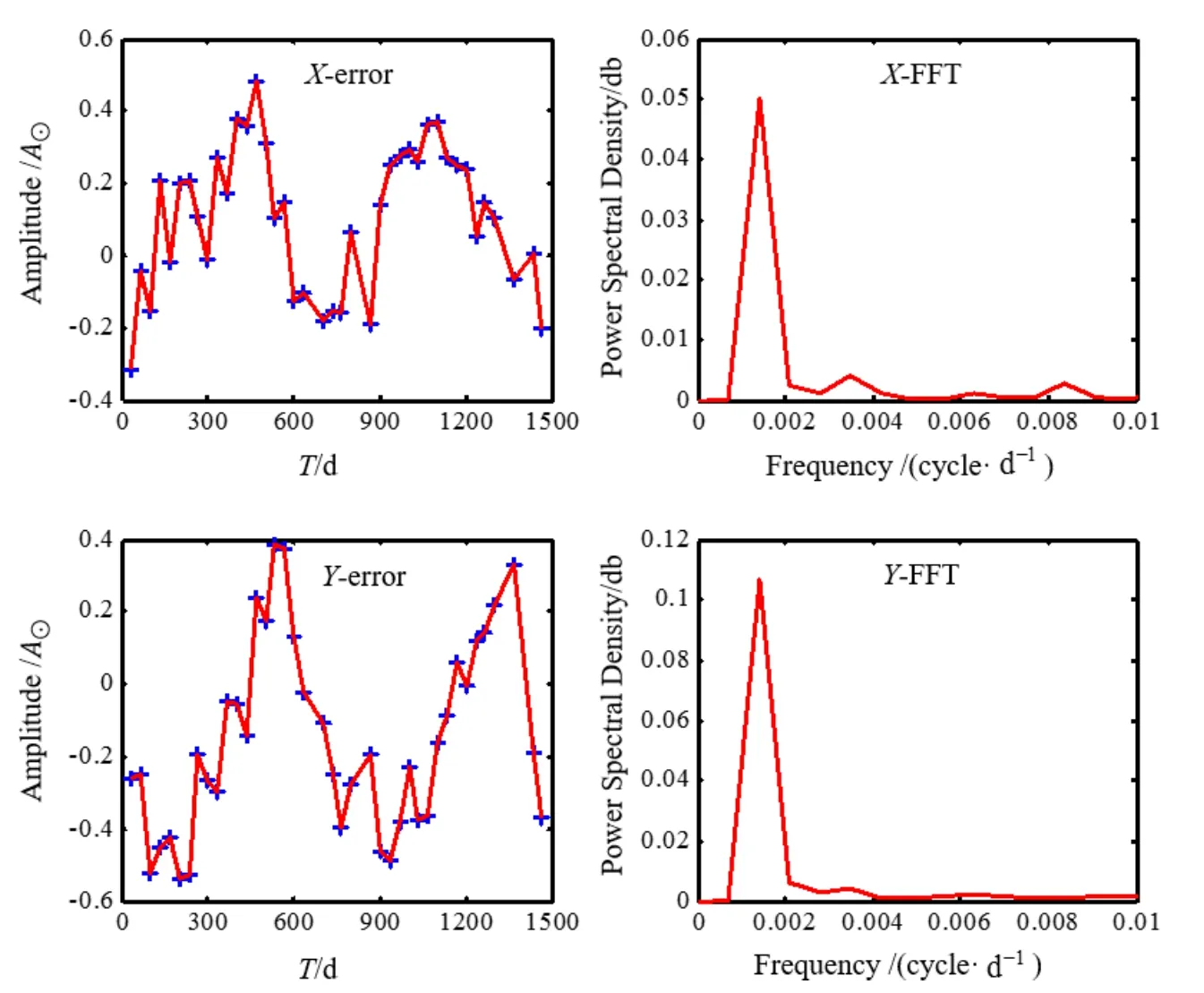
图3 模型A-3的x、y方向数据进行傅里叶分析的结果Fig.3 T he resu lts of x and y com p onen ts of the m odel A-3 with FFT

根据统计,LSQ和FFT均能实现观测数据的周期分析.模型A的精确周期为730 d,3个子模型进行FFT的结果分别为720 d、716.67 d和716.67 d,明显要好于LSQ的结果.

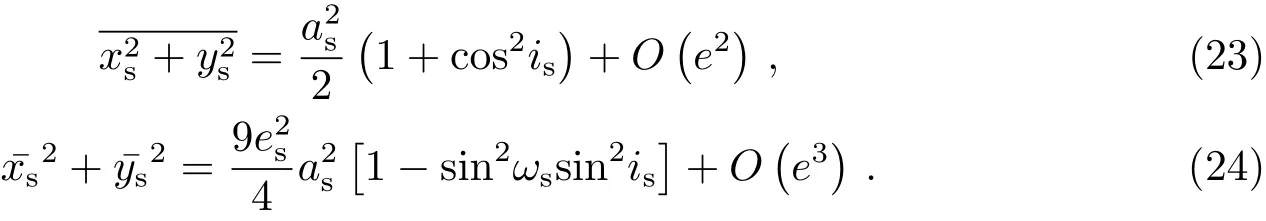
对序列{xs(tj),ys(tj),j=1,2,···,k}在时间域上作平均,可以获得如下关系式,假定已知行星质量mp、恒星的平近点角M、恒星的升交点经度Ω和恒星的近星点经度ω,可以由上述3个约束关系式(21)–(23)式,近似给出恒星的轨道半长径、偏心率和轨道倾角,这样将对7维参数空间扫描问题降低到4维参数空间扫描,可以显著提高计算效率.当然,在由观测时间序列计算上述平均值时,会产生计算误差,将会直接影响到上述约束条件的精度.

7 多行星系统的计算

坐标速度法可以作为天体测量法探测系外行星的基本方法,不仅是因为它可以用于小偏心率轨道计算,而且较容易将其推广到多行星系统,求解各个行星的参数(位置、速度及质量).下面仅推导由1颗恒星和2颗行星组成的三体系统中恒星观测方程计算具体关系式,n体问题的推导思路类似.

建立如图4所示惯性坐标系,恒星与两颗行星质量分别为Ms、m1和m2,O为系统的质量中心,空间位置矢量如图所示.

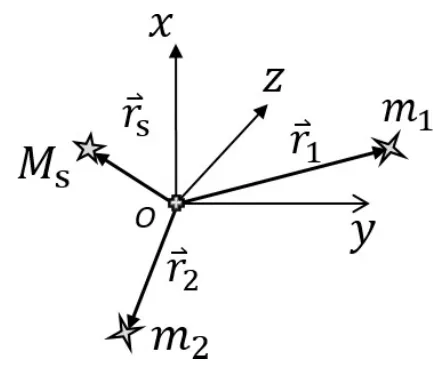
图4 三体运动坐标示意图Fig.4 T he coord inate’s sketch of the th ree-body m otion

3个天体对应的运动方程为

因系统质心为坐标原点,由质心运动定理知:

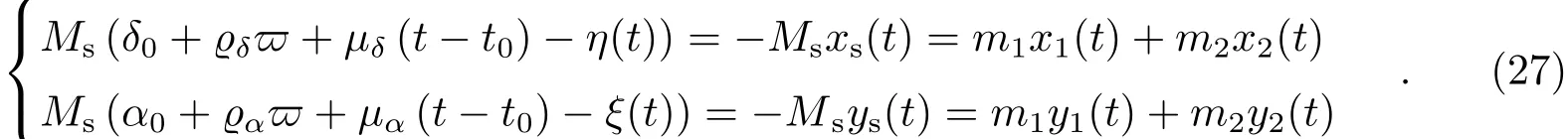
方程(25)左边分别用η′(t)、ξ′(t)表示,可将其改写为

由(24)–(25)式可求出行星运动方程为

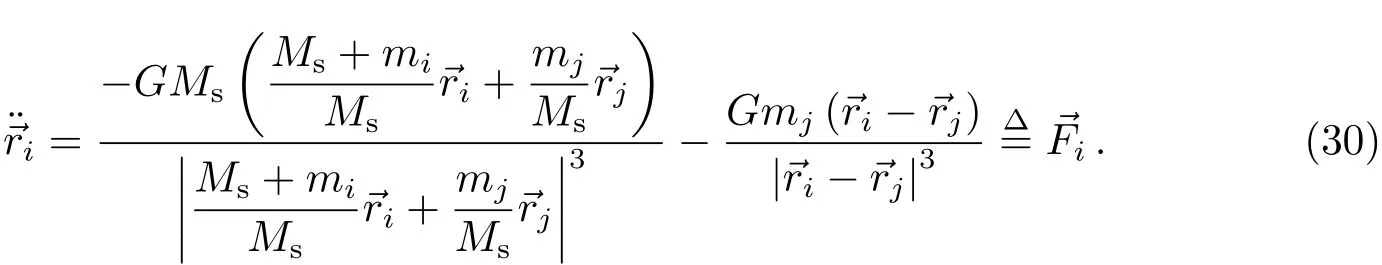
状态转移方程涉及到的初始条件为:当t=t0时,

这里,H为3阶单位矩阵.

8 结论与讨论

本文基于天体测量法给出的恒星空间位置参数序列,讨论了在求解行星质量和轨道参数时涉及的动力学条件方程计算问题;对于采用Kepler轨道根数和采用坐标速度描述形式分别给出了具体微分改正公式,同时也进行了初步必要的仿真模拟计算;通过天体力学二体问题运动关系式,对恒星空间位置时间序列做平均分析,推导出了待估参数间存在的3个约束条件关系式,可以显著提升计算效率.

本文没有对恒星自行和视差等天体测量参数做解算研究,以后若有实测数据,可根据实际情况作具体处理:或单独求解,或与行星轨道和质量一起求解.

[1]M ayor M,Q ueloz D.Natu re,1995,368:355

[2]M ichael P.T he Exop lanet Handbook.New York:Cam b ridge Un iversity P ress,2011:3-5

[3]Luisa G J,Lu is A,Barbara P.M NRAS,2014,443:260

[4]姜明达,肖东,朱永田.天文学进展,2012,30:214

[5]Dou J P,Zhu Y T,Ren D Q.Ch inese Jou rna l of Natu re,2014,36:124

[6]张牛,季江徽.天文学进展,2009,27:14

[7]Lin D N C,Ida S.A p J,1997,477:781

[8]Papaloizou J C B,Terquem C.M NRAS,2001,325:221

[9]金文敬.天文学进展,2013,31:375

[10]W right J T,How ard A W.Ap JS,2009,182:205

[11]Sara S.Exop lanets.A rizona:Un iversity of A rizona P ress,2010:327-329

[12]M ichael P,Joel H,G aspar B,et a l.A p J,2014,797:14

[13]Th iele T N.A stronom ische Nach rich ten,1883,104:245

Exop lanet Detection by A strom etric M ethod

XUWei-wei1,2,3,4LIAO Xin-hao1,3ZHOU Yong-hong1,3XU Xue-qing1,3

(1 Shanghai A stronom ica l O bserva to ry,Chinese A cadem y of Scien ces,Shanghai 200030) (2 Schoo l of Physica l Scien ce an d Techno logy,ShanghaiTech Un iversity,Shanghai 201210) (3 K ey Labo ra to ry of P laneta ry Scien ces,Chinese A cadem y of Scien ces,Shanghai 200030) (4 Un iversity of Chinese A cadem y of Scien ces,Beijing 100049)

Aswe known,the exoplanetsaremostly detected by themethodsof radial velocity and transit,only one is found by the astrometric method.As the data of the gaia to be released,astrom etry w ill becom e one of themost im portantmethod for detecting exoplanets gradually.Based on the position sequence of stars,this paper discusses the calculation of the equations of dynam ics conditions involved in solving themass and the orbit parameters of the planet.Due to the deficiency of the available theory(orbital elem ent m ethod),we put forward a new m ethod(coordinate velocity method).The differential correction formulae of the twomethodsare presented,aswell as the necessary simulation.In addition,themethod established in this paper can be app lied to themulti-planet system easily.

exoplanet,astrometry,celestialmechanics:orbit calculation and determ ination,m ethods:data analysis

P135;

A

10.15940/j.cnki.0001-5245.2016.04.004

2015-12-08收到原稿,2016-03-04收到修改稿

∗国家自然科学基金项目(11133004)和中国科学院先导B项目(XDBO9000000)资助

†1143880832@qq.com

‡xhliao@shao.ac.cn