基于深度学习技术的恒星大气物理参数自动估计∗

潘儒扬 李乡儒

(华南师范大学数学科学学院 广州 510631)

基于深度学习技术的恒星大气物理参数自动估计∗

潘儒扬 李乡儒†

(华南师范大学数学科学学院 广州 510631)

深度学习是当前机器学习、模式识别和人工智能领域中的一项热点研究技术,非常适用于处理复杂的大规模数据.基于深度学习理论构建了一个5层的栈式自编码深度神经网络,对恒星大气物理参数进行自动估计,网络各层的节点数分别为3821-500-100-50-1.使用美国大型巡天项目Sloan发布的Sloan D igital Sky Survey(SDSS)实测光谱以及由Kurucz的New Opacity D istribution Function(NEWODF)模型得到的理论光谱进行了实验验证,对有效温度(Teff)、表面重力加速度(lg g)和金属丰度([Fe/H])3个物理参数进行了自动估计.结果表明,栈式自编码深度神经网络的估计精度较好,其中在SDSS数据上的平均绝对误差分别为:79.95(Teff/K),0.0058(lg(Teff/K)),0.1706(lg(g/(cm·s−2))), 0.1294 dex([Fe/H]);在理论数据上的平均绝对误差分别是:15.34(Teff/K),0.0011(lg (Teff/K)),0.0214(lg(g/(cm·s−2))),0.0121 dex([Fe/H]).

恒星:基本参数,恒星:大气,恒星:丰度,方法:数据分析,方法:统计

1 引言

研究银河系中恒星性质是天体物理学的一个重要问题[1],LAMOST[2–4]和Sloan[5–7]等大规模巡天望远镜可以从银河系中观测到海量的恒星光谱数据,如何从这些海量光谱数据中自动估计出恒星大气物理参数对于研究恒星的性质具有重要意义.

深度学习[8]是机器学习、模式识别和人工智能领域中的一项热点研究技术.特别是,近年受到Google、百度、微软、Facebook等信息技术企业的大力推动,深度学习技术取得了长足的进展,并成功地应用在图像识别、视频分析、自然语言处理、电子商务数据分析和语音识别等领域.

深度学习在非线性关系探索和表示方面表现突出,适合处理复杂的大数据.恒星光谱与恒星大气物理参数之间存在着高度非线性关系,并且实测光谱是具有大量噪声的高维数据.因此,本文工作研究了深度学习技术在恒星大气物理参数估计中的应用.

2 深度学习

深度学习技术包括以下3种基本类型:栈式自编码、置信网和卷积神经网络.本文研究了栈式自编码在恒星大气物理参数估计中的应用,下文对该类型深度学习方法做进一步介绍.

栈式自编码学习方法又称为栈式自编码神经网络,实际上是一个多层前馈神经网络(Feedforward Neural Network).之所以称之为栈式自编码深度神经网络,是因为训练这个多层前馈神经网络,需要使用栈式自编码(Stacked Autoencoder)算法对它进行预学习(Pre-training),再结合线性回归网络做微调(Fine-tuning).下面分别介绍多层前馈神经网络、预学习以及微调.

2.1 多层前馈神经网络

2.1.1 多层前馈神经网络的网络结构

多层前馈神经网络的特点是数据从网络的输入层向输出层单向流动,一个共有p层(包含1个输入层,1个输出层和p−2个隐层)的多层前馈神经网结构如图1所示.

图1前馈神经网示意图.本图中未画出偏置项对应的节点.Fig.1 A sketch of a feed forw ard neu ral netw ork.T he b ias un its are not p resented in this sketch.

图1 中符号的上标(k)表示网络的层数标号,nk表示网络第k层的节点数.W(k)是一个nk×nk+1的矩阵,表示权重,b(k)是一个nk+1维的行向量,表示偏置.通常W(k)和b(k)也被统称为网络第k层和第k+1层之间的连接参数.fk是激活函数,常用的激活函数有sigmoid函数、恒等函数和双曲正切函数.a(k)表示第k层的输出,x和y分别表示网络的输入和输出.以上k=1,2,···,p−1.如无特殊说明,本文所述的向量均指行向量,且未将偏置项计入节点数中.

在一个前馈神经网络中,输入数据x=(x1,x2,x3,···,xn1)将沿着箭头的方向,由低层到高层逐步经过各层权重、偏置和激活函数的作用,转换为网络的输出y= (y1,y2,y3,···,ynp).这是一个迭代计算的过程,计算公式为

其中,a(1)=x,a(p)=y.(1)式是一种向量化表达,对于特定节点来说,(1)式可表示为

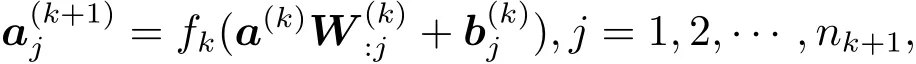
对于任意输入x,通过该前馈神经网络可得到一个输出y.因此,前馈神经网络实现了一个从输入空间到输出空间的函数映射关系,该映射关系可表示为y=hW,b(x),其中,下标W和b是神经网络的配置参数,分别表示神经网络的权重参数和偏置参数

参数W和b需要从训练数据中学习得到.

假设Str={(x(i),yi),i=1,···,N}是一个训练数据集,其中,N表示训练数据的数量,x(i)表示光谱,yi表示该光谱的参数,在本文研究中可以是有效温度、表面重力加速度或金属丰度三者之一.神经网络的配置参数W和b可通过以下目标函数学习得到

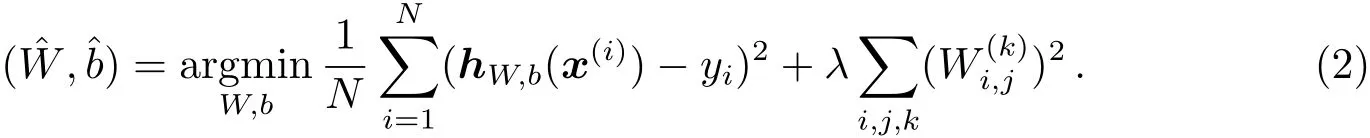
在目标函数(2)式中,等号右边的第1项度量了对经验数据的拟合误差(经验风险),第2项称为正则化项,抑制某些个别的参数过大,以提升所学习模型在未观测数据上的性能(相关文献中称之为泛化能力),λ为权重衰减系数,处理经验风险与泛化能力之间的折衷/平衡关系.

2.1.2 多层前馈神经网络的传统训练方法与不足

前馈神经网络的传统训练方法(即求解(2)式的方法)是BP(Back Propagation)算法[9].其基本思想是,首先根据经验随机生成一系列绝对值十分小的数作为前馈神经网络各层之间的初始连接参数(即(2)式中W和b的初始值),然后使用梯度下降法迭代求解连接参数最优值,每次迭代时连接参数的导数根据误差的反向传递得到.使用BP算法训练的多层前馈神经网络通常也被称为BP神经网络.

BP算法存在许多不足,其中较为严重的有:第一,(2)式是一个高度非凸的优化问题,当网络层数较多(网络层数大于4)时,单纯使用梯度下降法求解容易陷入较差的局部极小值;第二,当网络层数较多时,由于误差反向传播的特性,接近输入层的网络连接参数难以优化,致使结果较差,文献中将这种现象称之为“梯度弥散”.由于这两个典型的不足,直接使用BP算法训练层数较多的前馈神经网络,效果十分不理想.因此,传统的BP神经网络通常都是层数较少的浅层神经网络,很大程度上限制了神经网络的适用范围.

为了克服BP算法的不足,栈式自编码深度学习技术基于贪心算法的思想,将前馈神经网络的学习过程分为两个阶段:预学习和微调.在预学习阶段,从前到后依次使用自编码神经网络学习各个隐层与前一层之间的连接参数,该环节称之为栈式自编码.在微调阶段,首先用线性回归网络寻找到前馈神经网络最后一个隐层和输出层之间较优的连接参数;然后使用BP算法对所有较优的连接参数做整体上的优化和局部微调.下面分别介绍栈式自编码神经网络的预学习和微调.

2.2 预学习

栈式自编码算法的基础是自编码神经网络.下面首先介绍自编码神经网络,然后介绍栈式自编码算法.

2.2.1 自编码神经网络

自编码神经网络是一种特殊的3层前馈神经网络,结构如图2所示.其特殊性在于,网络输出层的节点数n3必须等于网络输入层的节点数n1,且网络的期望输出即是网络的输入x.

图2 自编码神经网络示意图.本图中未画出偏置项对应的节点.Fig.2 A sketch of an au toencoder neu ra l netw ork.T he bias un its are not p resen ted in th is sketch.

具体来说,当给定训练集Str后,学习模型(见(2)式)将尝试寻找适合的权重W和偏置b,使得网络的输出值hW,b(x)成为网络输入值x的一种近似重构.这样输入值x将沿着图中箭头的方向在W(1)、b(1)和f1的作用下被转换成a(2)(见(1)式),这称为网络的编码过程;而a(2)将沿着图中箭头的方向在W(2)、b(2)以及f2的作用下被转换为x的一种近似重构,这称为网络的解码过程.

一般使用传统的BP算法训练自编码神经网络,训练好一个自编码神经网络后,其网络的隐层激活值a(2)就是网络输入值的一种低维表达,所以通常使用自编码神经网络实现特征提取.

2.2.2 栈式自编码算法

在多层前馈神经网络中,所有隐层应当完成特征提取的过程,所以在预学习时,可以使用一系列自编码神经网络寻找前馈神经网络除输出层之外各层之间较优的连接参数.具体来说,当训练好一个自编码神经网络后,可以丢弃掉自编码神经网络隐层和输出层之间的连接参数W(2)和b(2),只保留输入层和隐层之间的连接参数W(1)和b(1)作为多层前馈神经网络第1层和第2层之间较优的连接参数.在此基础上,为了寻找前馈神经网络第2层和第3层之间较优的连接参数,可以将之前训练好的自编码神经网络的隐层激活值a(2)作为下一个自编码神经网络的输入值,训练下一个自编码神经网络.依此类推,可以使用一系列自编码神经网络寻找到前馈神经网络中除输出层以外各层之间较优的连接参数,这就是栈式自编码算法.

2.3 微调

本文的栈式自编码神经网络微调时需要使用到一个线性回归网络,线性回归网络是一种特殊的2层前馈神经网络,其特殊性体现在网络的激活函数是恒等函数.由于线性回归网络的结构十分简单,所以不详细介绍.

微调分为两个步骤:第一,以预学习中最后一个自编码神经网络的隐层激活值作为线性回归网络的输入值,以回归问题的因变量作为线性回归网络的期望输出(本文中回归问题的因变量就是一个恒星大气物理参数),使用传统的BP算法训练线性回归网络,并将训练所得的连接参数作为前馈神经网络最后一个隐层和输出层之间较优的连接参数;第二,联合所有自编码神经网络寻找到的较优连接参数和线性回归网络寻找到的较优连接参数作为整个前馈神经网络的初始连接参数(见图3),并使用梯度下降算法进一步训练整个前馈神经网络,这一步和BP算法是类似的,只是网络的初始连接参数不再是随机得到的,而是上文提到的较优的连接参数.

图3大致描绘了使用深度学习理论训练一个多层前馈神经网络成为栈式自编码神经网络的过程,图中每个直角矩形代表一个神经网络,直角矩形中每个圆角矩形代表神经网络中的一层节点,圆角矩形之间的实线箭头代表网络两层之间的连接参数,图的上半部分有一系列自编码神经网络和一个线性回归网络,下半部分则是一个多层前馈神经网络(也是栈式自编码神经网络).图中的虚线箭头代表英文标注的某个具体操作,3个小黑点是省略号.

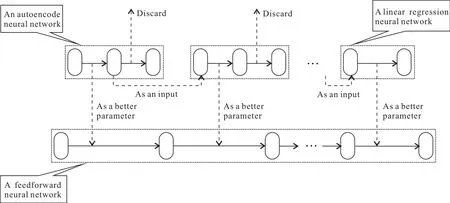
图3 深度学习过程示意图Fig.3 A sketch of deep learn ing

2.4 栈式自编码神经网络与BP神经网络的对比

栈式自编码神经网络与BP神经网络都是多层前馈神经网络,但是,栈式自编码神经网络通常层数较多,学习和泛化能力更强.同时,它们的训练方法也不同,BP神经网络直接使用随机数做为前馈神经网络的初始连接参数,然后用梯度下降算法训练网络;而栈式自编码神经网络将训练过程分为预学习和微调两个阶段,寻找到前馈神经网络各层之间较优的连接参数作为初始连接参数后,再使用梯度下降算法训练网络.

栈式自编码神经网络的训练方法可以有效克服本文2.1.2小节第2自然段所提到的“局部极小值”和“梯度弥散”等问题,使得栈式自编码神经网络表现出远超BP神经网络的学习效果,并在恒星大气物理参数估计问题上获得较好的结果.下文分别在美国大型巡天项目Sloan发布的SDSS实测光谱以及由Kurucz的NEWODF模型得到的理论光谱上进行了实验验证.

3 实验

本文使用各层节点数分别为3821-500-100-50-1的5层栈式自编码神经网络进行了两个实验,分别是在Sloan发布的SDSS实测光谱数据集上进行的实验,以及在由Kurucz的NEWODF模型得到的理论光谱数据集上进行的实验.

为了训练栈式自编码神经网络,并对网络的回归效果进行评价,需要将各实验的数据集都分成两个子集:训练集,测试集.令Str={(x(i),yi),i=1,···,N}表示训练集,(x(i),yi)是一个训练样本.其中,x(i)=(x,x,···,x)是一个向量,表示第i条恒星光谱数据,表示观测到的光谱流量值;yi是一个数,表示与x(i)对应的恒星大气物理参数(文中yi可以在适当的时候表示有效温度(Teff),表面重力加速度(lg g)和金属丰度([Fe/H])的三者之一).N表示训练集所包含的样本数.类似地可以用Ste表示测试集.

3.1 实验的评价标准

为了便于与文献中的相关研究结果进行比较,本文使用平均绝对误差(Mean Absolute Error,MAE),平均误差(Mean Error,ME)和误差的标准差(Standard Deviation, SD)这3种误差评价标准对所建议方案做了评估研究.

在测试集Ste上,3个误差评价标准MAE、ME和SD分别定义如下:

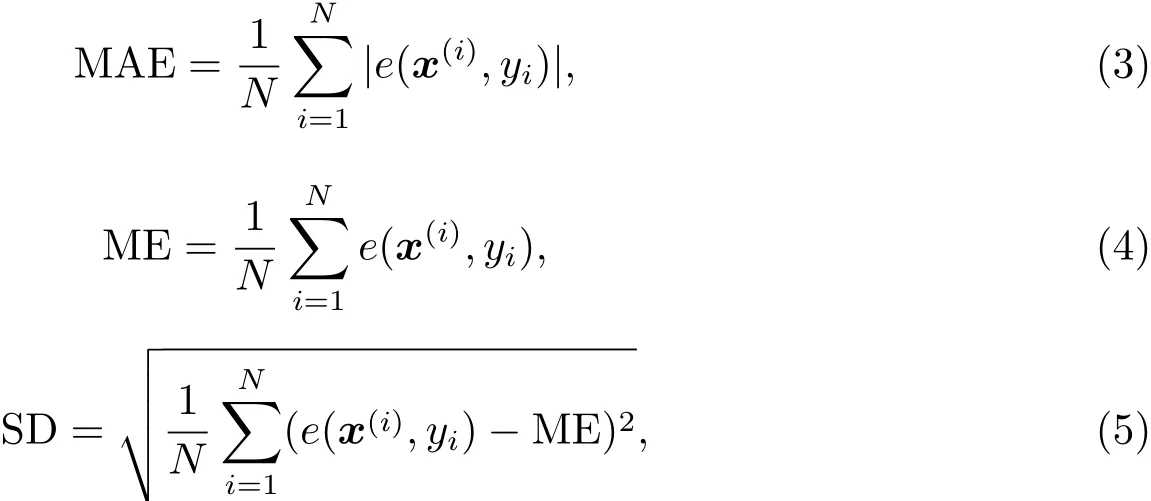
其中,N表示测试集Ste的样本数,

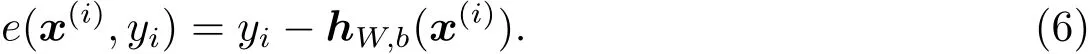
hW,b(x(i))表示训练好的栈式自编码神经网络的输出值,也即实验中对某个恒星大气物理参数的估计值.

3.2 数据预处理

实验前需要对训练数据进行预处理,首先进行逐光谱数据归一化,即每条光谱向量都除以该光谱向量的模值,然后进行逐流量特征[0,1]区间化,即每个流量特征都减去该流量特征在训练集中的最小值并除以最大值和最小值的差.对于测试数据也需要进行类似的预处理,只是在逐流量特征[0,1]区间化时使用训练集中得到的最大值和最小值.同时,为了能够更好地对温度(Teff)的估计效果进行描述,实验也对温度Teff以10为底的对数值lg Teff进行了回归估计.

3.3 在实测数据上的实验研究

3.3.1 实验数据集说明

选取50000条美国大型巡天项目Sloan发布的SDSS实测光谱数据,及每条光谱对应的3个恒星大气物理参数作为实验数据集.每条光谱具有3821个流量特征;3个恒星大气物理参数分别是有效温度(Teff),表面重力加速度(lg g)和金属丰度([Fe/H]),参数的范围分别为:[4088,9740]K(Teff),[1.015,4.998](lg(g/(cm·s−2))),[−3.497,0.268]dex ([Fe/H]).在这50000条实测光谱中随机选取5000条光谱以及它们对应的恒星大气物理参数作为训练集Str,剩余的45000条光谱以及它们对应的恒星大气物理参数作为测试集Ste.

3.3.2 实验过程

本文设计了各层节点数分别为3821-500-100-50-1的栈式自编码神经网络进行实验,为了训练栈式自编码神经网络需要进行预学习和微调(详见本文2.2和2.3小节).在预学习阶段,使用栈式自编码算法(详见本文2.2.2小节)训练了3个自编码神经网络(详见本文2.2.1小节),它们的各层节点数分别为3821-500-3821,500-100-500,100-50-100,激活函数都是sigmoid函数,学习模型(即(2)式)的损失函数都是交叉熵函数.值得一提的是,虽然本文的实验需要估计3个恒星大气物理参数,但由于预学习只涉及到光谱数据而不涉及到恒星大气物理参数,所以预学习只需要进行1次,但需要将预学习的结果保存下来,以便多个微调共用.在微调阶段,首先,针对某1个恒星大气物理参数,训练1个线性回归网络,它的节点数为50-1,输入值为预学习中节点数为100-50-100的自编码神经网络的隐层激活值,期望输出为1个恒星大气物理参数,学习模型的损失函数为最小二乘函数;接着将所有自编码神经网络和1个线性回归网络寻找到的较优的连接参数作为多层前馈神经网络(详见本文2.1小节)的初始连接参数,使用梯度下降算法整体训练多层前馈神经网络.按照这样的深度学习方法训练好的多层前馈神经网络,就是本文实验使用的5层栈式自编码神经网络了.需要说明的是,由于本文的实验需要分别对3个恒星大气物理参数进行自动估计,所以需要进行3次微调,它们共用前面保存的预学习结果.

3.3.3 实验结果与分析

在45000条SDSS光谱数据组成的测试集Ste上的平均绝对误差分别是:79.95 K (Teff),0.1706(lg(g/(cm·s−2))),0.1294 dex([Fe/H]).更多测试结果请见表1.

为了便于与已有的相关研究做比较和探讨,文献中的典型研究结果也在表1中列出.在相关文献使用的各种方法中,OLS和SVRl是线性的估计方法,而ANN、MAχ和SVRG是非线性的估计方法.对比线性估计方法和非线性估计方法,可以发现非线性估计方法的误差均小于线性估计方法的误差,这说明恒星光谱与恒星大气物理参数之间隐藏着高度非线性关系,需要使用非线性的估计方法将这些非线性关系解析出来才能得到精度较高的估计结果.这也是本文采用栈式自编码深度神经网络,并使用sigmoid函数作为网络激活函数的原因.sigmoid函数的表达式见(7)式,它是一种S型的函数,函数的两端较平缓而不敏感,函数的中间较陡峭而十分敏感.sigmoid函数的这种性质,不仅可以解析数据中的非线性关系,而且还可以在一定程度上抑制数据中的噪声.

与文献中的典型结果相比,上述实验结果表明栈式自编码深度神经网络在基于光谱的恒星大气物理参数估计精度上有不错的潜在优势;本文实验中的ME更接近于0,这说明本文的估计结果更近似于无偏;同时本文实验的SD也非常小,说明本文的估计结果十分稳定,具有良好的鲁棒性.值得一提的是,本文实验时的训练样本只有5000条,而测试样本有45000条,使用的训练样本数远远小于相关文献,而使用的测试样本数远远大于相关文献,但实验的结果却优于或者接近相关文献,这说明本文使用的估计方法的学习能力和泛化能力均表现较好.

特别是,与相关文献中基于ANN的研究方案相比,本文估计结果远远优于ANN的估计结果.二者都是基于神经网络的,不同的是ANN是传统的人工神经网络,而本文使用的是基于深度学习理论的栈式自编码深度神经网络.栈式自编码深度神经网络基于深度学习理论,使用更为先进的神经网络训练方法训练一个多层前馈神经网络,能够有效克服“梯度弥散”等传统神经网络的不足,增大网络层数,具备比传统的浅层神经网络更强的复杂数据解析能力、学习能力和泛化能力,从而在恒星大气物理参数估计问题上表现更好.

现有结果表明,文献[15]方案的性能良好.实际上,文献[15]方案的重点是通过机器学习的方法自动检测恒星大气物理参数的特征,剔除冗余和不相关流量成分,即解决用什么的问题.本文方案的目标是,基于给定的流量信息,探索怎样整合数据信息才能有利于恒星大气物理参数的估计,即探索如何用的问题.因此,将文献[15]中的特征与本文推荐的深度学习网络相结合用于恒星参数的估计,是一项值得进一步研究的内容.

3.4 在理论数据上的实验研究

3.4.1 实验数据集说明

选取18969条由Kurucz的NEWODF模型得到的理论光谱,以及对应的3个恒星大气物理参数作为实验数据集.每条光谱具有3821个流量特征;3个恒星大气物理参数分别是有效温度(Teff),表面重力加速度(lg g)和金属丰度([Fe/H]),参数的范围分别为: [4000,9750]K(Teff),[1,5](lg(g/(cm·s−2))),[−3.6,0.3]dex([Fe/H]).在这18969条理论光谱中随机选取5000条光谱以及它们对应的恒星大气物理参数作为训练集Str,剩余的13969条光谱以及它们对应的恒星大气物理参数作为测试集Ste.

3.4.2 实验结果

在理论光谱上同样设计了各层节点数分别为3821-500-100-50-1的栈式自编码神经网络进行实验.实验过程与实测光谱上的实验类似,这里不再赘述.在13969条理论光谱数据测试集上的平均绝对误差分别是:15.34 K(Teff),0.0214(lg(g/(cm·s−2))),0.0121 dex([Fe/H]),更多结果及相关文献中的典型研究结果请见表2.实验结果同样验证了栈式自编码神经网络具有很大优势,非常适合处理恒星大气物理参数估计问题.

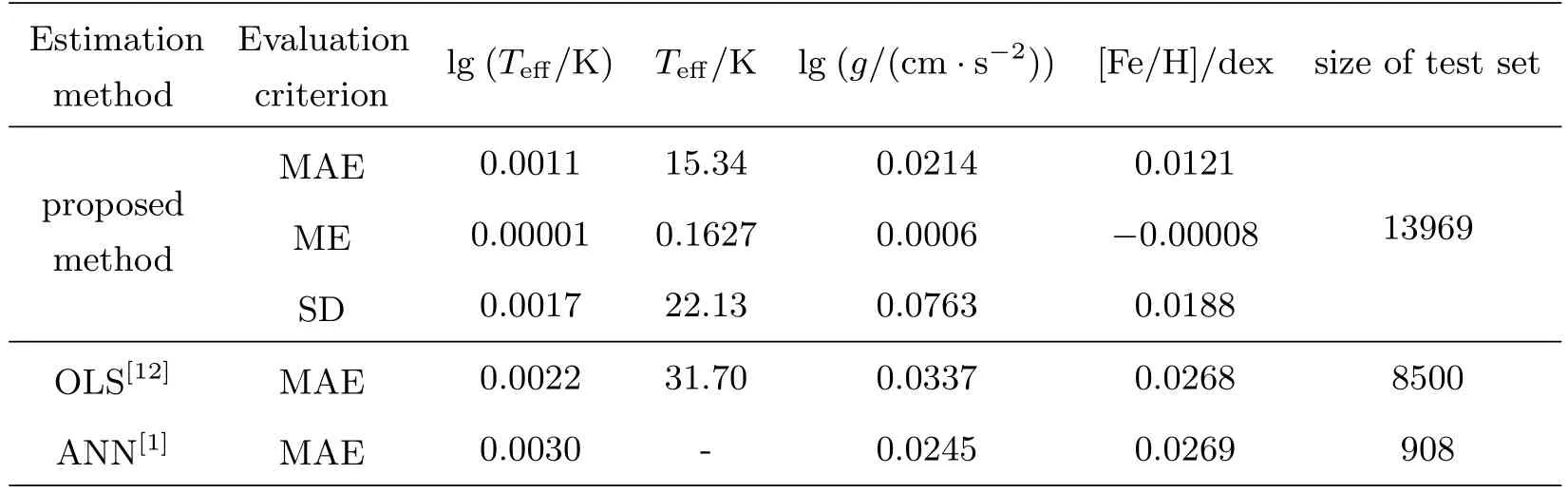
表2 在理论光谱上的实验结果以及相关文献中的典型结果.理论光谱由NEWODF模型计算得到.Tab le 2 The exp erim en tal resu lts on syn thetic sp ectra com pu ted with the NEW ODF m od el and som e typ ical resu lts in the related literatu re

4 总结

深度学习是近年提出的一种新的机器学习技术,与传统机器学习技术相比,使用深度学习技术构建的深度神经网络具有更强的学习和泛化能力,适合处理复杂的大数据.本文研究了深度学习技术在恒星大气物理参数估计中的应用,使用深度学习技术训练栈式自编码深度神经网络对恒星大气物理参数中的有效温度(Teff),表面重力加速度(lg g)和金属丰度([Fe/H])进行回归估计.实验时,在实测数据上的平均绝对误差分别是:79.95 K(Teff),0.0058(lg(Teff/K)),0.1706(lg(g/(cm·s−2))),0.1294 dex([Fe/H]);在理论数据上的平均绝对误差分别是:15.34 K(Teff),0.0011(lg(Teff/K)),0.0214(lg (g/(cm·s−2))),0.0121 dex([Fe/H]).与文献中的同类研究相比,该方案的显著优势是估计精度高.

[1]Fiorentin P R,Bailer-Jones C A L,Lee Y S,et al.A&A,2007,467:1373

[2]Reid B A,Sam ush ia L,W h ite M,et a l.M NRAS,2012,426:2719

[3]S´anchez A G,Sc´occo la C G,Ross A J,et a l.M NRAS,2012,425:415

[4]Ogu ri M,Bay liss M B,Dah le H,et a l.M NRAS,2012,420:3213

[5]Cu i X Q,Zhao Y H,Chu Y Q,et a l.RAA,2012,12:1197

[6]Luo A L,Zhang H T,Zhao Y H,et a l.RAA,2012,12:1243

[7]Zhao G,Zhao Y H,Chu Y Q,et a l.RAA,2012,12:724

[8]H in ton G E,Sa lakhu td inov R R.Science,2006,313:504

[9]Rum elhart D E,H in ton G E,W illiam s R J.Natu re,1986,323:533

[10]Jofr´e P,Panter B,Hansen C J,et al.A&A,2010,517:57

[11]Li X R,W u Q M J,Luo A L,et a l.A p J,2014,790:105

[12]谭鑫,潘景昌,王杰,等.光谱学与光谱分析,2013,33:1397

[13]常丽娜,张培爱.天文学报,2015,56:26

[14]Chang L N,Zhang P A.ChA&A,2015,39:319

[15]高伟,李乡儒.天文学报,2016,57:389

Stellar A tm ospheric Param eterization Based on Deep Learn ing

PAN Ru-yang LIXiang-ru

(Schoo l of M a them a tica l Scien ces,Sou th China Norm a l Un iversity,G uangzhou 510631)

Deep learning is a typical learning method w idely studied in machine learning,pattern recognition,and artificial intelligence.This work investigates the stellar atm ospheric parameterization p roblem by constructing a deep neural network with five layers.The proposed scheme is evaluated on both real spectra from Sloan Digital Sky Survey(SDSS)and the theoretic spectra com puted with Kurucz’s New Opacity Distribution Function(NEWODF)model.On the SDSS spectra,the mean absolute errors(MAEs)are 79.95 for the effective tem perature(Teff/K),0.0058 for lg (Teff/K),0.1706 for surface gravity(lg(g/(cm·s−2))),and 0.1294 dex for metallicity ([Fe/H]),respectively;On the theoretic spectra,the MAEs are 15.34 for Teff/K,0.0011 for lg(Teff/K),0.0214 for lg(g/(cm·s−2)),and 0.0121 dex for[Fe/H],respectively.

stars:fundamental parameters,stars:atmospheres,stars:abundances, methods:data analysis,methods:statistical

P144;

A

10.15940/j.cnki.0001-5245.2016.04.001

2015-11-10收到原稿,2016-01-29收到修改稿

∗国家自然科学基金项目(61273248,61075033)、国家自然科学基金委员会–中国科学院天文联合基金项目(U1531242)和广东省自然科学基金项目(2014A030313425,S2011010003348)资助

†xiangru.li@gm ail.com