综合脉冲星时间尺度∗

尹东山高玉平赵书红

(1中国科学院国家授时中心西安710600)

(2中国科学院时间频率基准重点实验室西安710600)

(3中国科学院大学北京100049)

综合脉冲星时间尺度∗

尹东山1,2,3†高玉平1,2赵书红1,2

(1中国科学院国家授时中心西安710600)

(2中国科学院时间频率基准重点实验室西安710600)

(3中国科学院大学北京100049)

由于截然不同的物理机制,毫秒脉冲星可产生与原子时尺度完全不同的另一类时间尺度.利用长期的脉冲星计时观测数据可建立综合脉冲星时间尺度,但通常脉冲星计时观测是非等间隔采样,并且有些脉冲星的观测间隔过长等,这些因素均对综合脉冲星时间尺度的产生造成很大的困难.因此,提出了一种新的算法来计算综合脉冲星时间尺度,即:首先选用三次样条插值方法进行内插,并使观测数据间隔均匀;其次采用Vondrak滤波方法对观测序列进行平滑处理并去除高频噪声;最后再利用加权算法产生综合脉冲星时间尺度.利用NANOGRAV(North American Nanohertz Observatory for Gravitational Waves)最新发布的长达9 yr的观测数据,计算得到了综合脉冲星时间尺度,它的长期稳定度(取样间隔大于1 yr)优于3.4×10−15.研究结果表明:这种方法可有效降低脉冲星计时残差中的噪声影响,同时可提高综合脉冲星时间尺度的长期稳定度.

时间,脉冲星,方法:观测,数据分析

1 引言

目前,国际原子时TAI(International Atomic Time)是准实时计算的时间尺度,随着大量的高精度原子钟和基准钟的涌现,以及原子时算法的改进,TAI的精度得到了不断提高.但由于考虑到实时性的影响,TAI必须每月进行一次计算,且在计算中受到很多约束条件限制,精度会在一定程度上受到影响,因此TAI不是TT(Terrestrial Time)的最优实现.为了提供更完美的原子时时间尺度,BIPM(International Bureau of Weights and Measures)提供了另一种事后计算的时间尺度,即TT(BIPM).TT(BIPM)每年计算一个新的版本,利用了所有可用的基准钟的数据计算得到TT的事后实现,在计算时间区间内对所采用的基准钟加入了黑体辐射以及其他改正,并对频率进行平滑和插值后得到TT(BIPM),这使得TT(BIPM)比TAI更准确也更稳定,因此TT(BIPM)可用作综合脉冲星时间尺度的参考时间.

由于与原子钟截然不同的物理机制,毫秒脉冲星可产生与原子时尺度完全不同的另一类时间尺度,也是理想时间尺度的一种实现方式,同样具有稳定、准确、可测量的特性[1−2].在2012年,国际天文学联合会时间委员会已经成立了一个脉冲星时间尺度工作组,协调该领域的国际合作,即说明了国际上开始重视综合脉冲星时间尺度研究.但一般情况下,由于脉冲星计时观测是非等间隔采样、采样率远远低于原子时的比对测量、脉冲星钟模型与计时噪声不同于原子钟的模型等,这些因素均对综合脉冲星时间尺度的计算造成很大的困难,因此脉冲星时间尺度算法是研究的重点.

本文基于NANOGRAV最新发布的长达9 yr的观测数据,利用新的算法计算综合脉冲星时间尺度,分析了脉冲星时间残差中的噪声影响,并评定了综合脉冲星时间尺度的稳定度.

2 算法原理

2.1 Vondrak滤波

Vondrak滤波方法不需要了解观测资料的变化规律,就能够对等间隔或非等间隔的观测资料进行有效平滑.Vondrak滤波实质上类似于单边滤波器,通过选择一个合适的截断频率,以保证尽可能多地保存有用信号,在数据处理中可以作为数字滤波器使用.

设观测资料x(ti)(i=1,2,···,N),Vondrak滤波的基本准则为[3]:

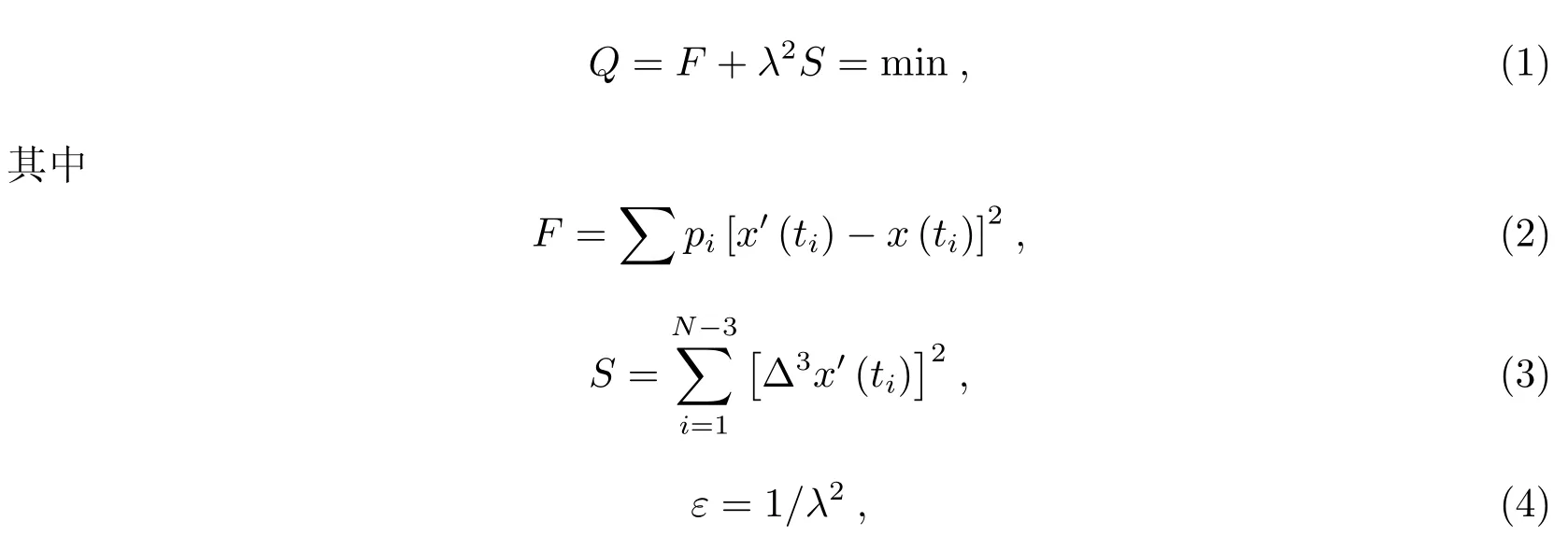
2.2 经典加权算法

设钟组中有n台脉冲星钟,其读数为hi(t),i=1,2,···,n,依据经典加权算法,计算得到一个时间尺度TA(t),一般形式为:

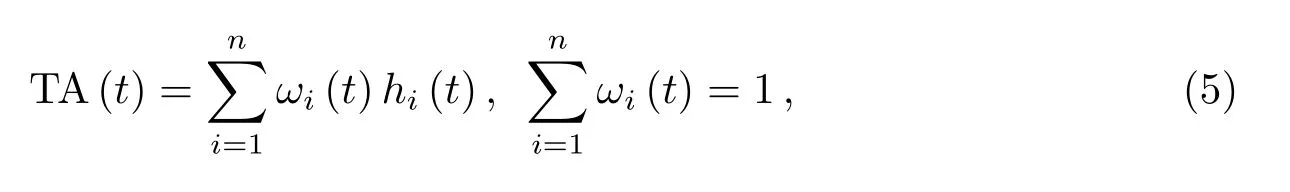
ωi(t)为钟clocki的权重.时间尺度TA(t)的噪声是钟组中所有钟的噪声加权和:

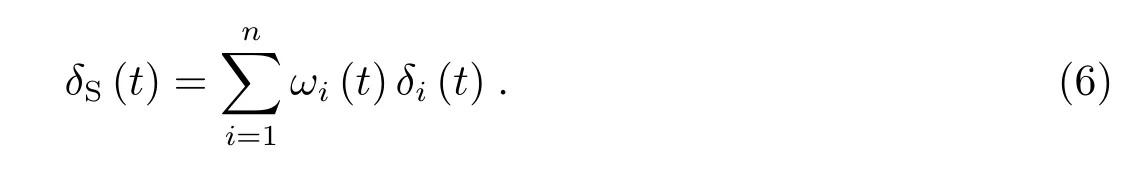
为了使综合钟的噪声δS(t)最小,通常以如下(7)式决定权重: )

利用每台钟相对于TA(t)的数据,计算阿伦方差或标准方差σ2i,根据(7)式计算得到每台钟的权重.

2.3 σz(τ)估计方法

由于脉冲星的自转相位、频率、自转变慢速率和相应天体测量参数应用计时模型已经精确测定,所以计时残差的三次差是脉冲星计时残差中剩余的最低阶偏差,因此σz(τ)是适用于脉冲星时间稳定度分析研究的估计方法[1].σz(τ)估计方法的计算流程如下:

(1)按观测时间顺序进行先后排序,将观测时间、计时残差以及误差分别记为ti、xi、σi,i=1,2,···,n,所取数据的总时间跨度为T=tn−t1.

(2)求出σz(τ),将这些数据按观测时间顺序连续分成时间间隔为τ的子序列.设t0为任意参考时刻,在每个子序列里应用三次多项式,如下式所示:

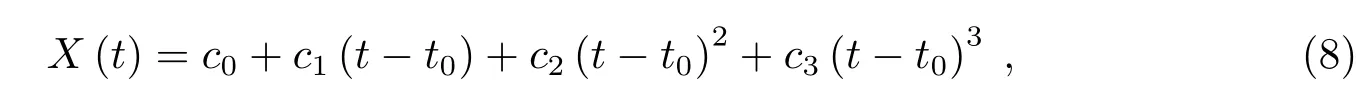
式中ci(i=0,1,2,3)为待拟合的系数.对(8)式进行最小二乘拟合,使得[(xi−X(ti))/σi]2为最小.定义σz(τ)为:

其中⟨⟩是指所有子序列的加权平均,权重反比于c3的误差平方值.

3 综合脉冲星时间尺度的算法

由于脉冲星计时观测是非等间隔采样,采样率也远远低于原子时的比对测量等,这些因素均对综合脉冲星时间尺度的产生造成很大的困难,因此脉冲星时间尺度算法是研究的重点.综合脉冲星时间尺度的新算法流程为:

(1)选用三次样条插值方法来加密观测数据,并使观测数据间隔均匀.

(2)采用Vondrak滤波方法来对观测序列进行平滑处理并去除高频噪声.

(3)利用加权算法产生综合脉冲星时间尺度,并最终对综合脉冲星时间尺度进行稳定度分析.具体的计算框图如图1所示.

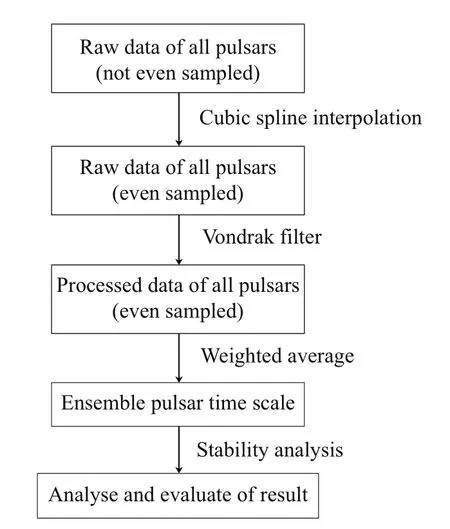
图1 综合脉冲星时间尺度算法框图Fig.1 The schematic of the algorithm of the ensemble pulsar time scale

4 试验结果及分析

4.1 试验数据介绍

我们选用了NANOGRAV最新发表的9 yr来所观测的37颗毫秒脉冲星的计时观测数据,这些数据由GBT(Green Bank Telescope)和ARECIBO望远镜观测得到,因为PSR B1937+21所展现出的计时噪声无法建立准确模型并加以改正,而且其噪声水平明显高于白噪声,所以剔除了这颗脉冲星的数据.其余36颗脉冲星观测数据的详细信息列于图2和表1中[4],表1列出了名称、自转周期(Period)、色散延迟量(Dispersion Measurement,DM)、拟合残差(Post- fit residual)、数据跨度(Span)、观测数据个数(Nobs)、初始历元(First epoch)与结束历元(Last epoch)等基本参数.其中所有脉冲星拟合后的计时残差均由TEMPO2处理得到,历表选用DE421太阳系行星质心历表[5−7].

4.2 计算结果及分析

为了不降低脉冲星时间尺度的稳定度,我们首先利用三次样条插值方法将原始观测数据插值为等间隔的数据,其次采用Vondrak滤波方法对处理后的等间隔数据进行滤波,其目的是尽量消除高频噪声,最后再利用新的算法计算综合脉冲星时间尺度,并对其稳定度进行分析.

4.2.1 三次样条插值

从图2和表1中可以看出,NANOGRAV的观测数据一般比较稀疏,并且数据点之间的间隔不均匀.为此我们尝试了多种不同的插值方法来增加数据点的个数,使数据点的采样间隔均匀化.在尝试了线性插值、二次项插值、三次样条插值等方法之后,结果显示三次样条插值能提供最优的数据序列,此方法是数据处理中常用的方法,具体过程略去.

需要特别注意的是,由于不同观测数据序列的时间跨度不同,并且观测数据个数差异也比较大,因此我们只对观测数据在其观测时间跨度内进行三次样条插值,目的是保证观测数据的可靠性和准确性,如果进行长时间的外推,势必影响到脉冲星观测数据的精度,进而会降低生成的综合时间尺度的稳定性.

图2 NANOGRAV 36颗源的拟合残差,观测历元从53216(MJD)至56599(MJD)Fig.2 The post- fit residuals of 36 pulsars included in NANOGRAV,within an observation duration from 53216(MJD)to 56599(MJD)

4.2.2 Vondrak滤波降噪分析

由于脉冲星观测受到宇宙背景辐射、射电频段的人为干扰、星际介质、设备的热噪声等因素影响,会导致脉冲星观测数据中包含高频噪声,因此在计算综合脉冲星时间尺度之前,对脉冲星观测数据进行降噪处理.本文选用Vondrak滤波方法来降低观测数据中的高频噪声,以脉冲星J1012+5307为例,图3给出了滤波前后的计时残差曲线图. Vondrak平滑因子选为1×10−9,从图3、图4和图5中可以看出,滤波后的曲线能够反映出脉冲星数据的细节,实测的观测数据相对于滤波后曲线值的残差在零值附近上下波动,且残差的分布服从高斯分布,符合相位白噪声即高频噪声的性质.

表1 文中用到的36颗毫秒脉冲星的详细参数Table 1 The detailed parameters of 36 millisecond pulsars included in this paper

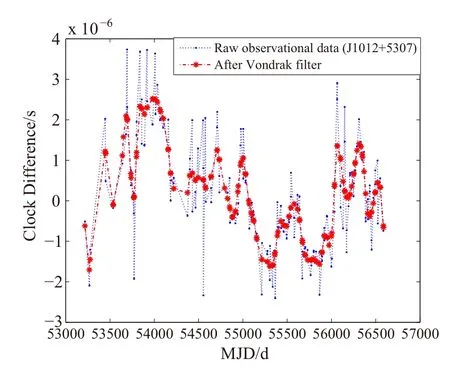
图3 Vondrak滤波前(点线)后(点虚线)PSR J1012+5307的计时残差Fig.3 The post- fit residuals of PSR J1012+5307 before(dotted line)and after(dot-dashed line)the Vondrak filter

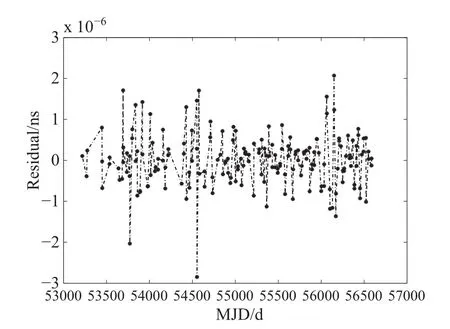
图4 原始观测数据与滤波曲线的相位差Fig.4 The phase di ff erence between the raw data and the filtered data

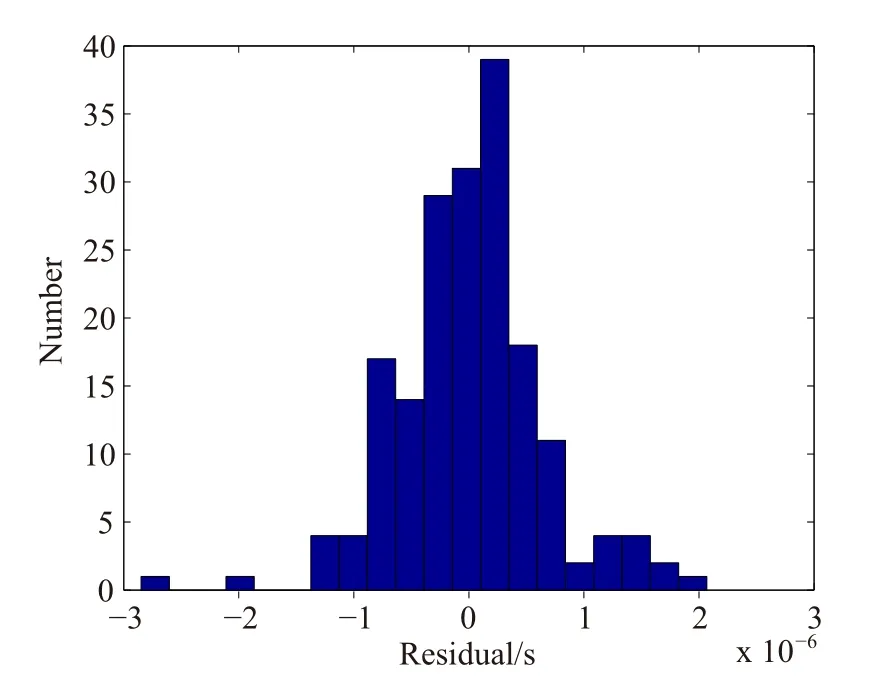
图5 原始数据与平滑曲线值的残差分布图Fig.5 The residual distribution between the raw data and the filtered data

4.2.3 综合脉冲星时间尺度

对36颗毫秒脉冲星的观测数据采用了三次样条插值以及Vondrak滤波算法后,采用加权算法对处理后的观测数据计算,最终获得综合脉冲星时间尺度.由于各脉冲星的观测时间跨度是不同的,因此在相同的观测时间上毫秒脉冲星的个数是不同的,这也是其与惯用的加权算法的不同之处.最终计算的脉冲星时间尺度如图6所示[8].

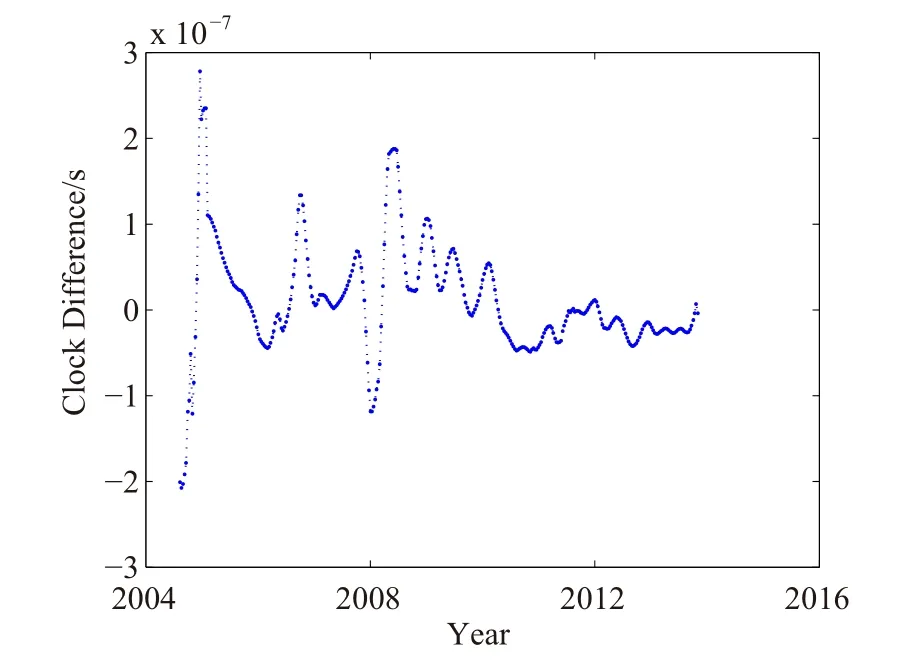
图6 综合脉冲星时间尺度Fig.6 The ensemble pulsar time scale

图6 所示为综合脉冲星时间尺度,参考时间为TDB(Barycentric Dynamic Time),均方根为0.056µs.在最初的4∼5 yr内(2009年之前),数据的波动幅度较大,而在2009年之后数据的波动幅度便明显减小,这主要由两个原因引起:(1)观测设备更新,主要是数据处理终端的更新,用GUPPI和PUPPI分别取代了GASP和ASP;(2)后期加入大批观测精度更高、计时残差更小的毫秒脉冲星的观测数据.

选用σz(τ)估计方法来分析最终生成的脉冲星时间尺度的稳定性,图7给出了综合脉冲星时间尺度的σz(τ)结果[9],当采样间隔小于100 d时,其不稳定度大于1×10−14,而当采样间隔大于100 d时,其不稳定度小于1×10−14.从结果可以看出,脉冲星时间尺度有很好的长期频率稳定度,但短期频率稳定度不佳.分析其原因,当取样间隔小于80 d时,影响频率稳定度的主要原因是频率闪烁噪声和随机游走频率噪声,这两类噪声应该是由系统噪声引起的,例如脉冲星自转的不规则性、观测系统噪声或星际闪烁噪声.而当采样间隔大于80 d时,噪声的主要成分是频率白噪声,通常是由观测噪声引起的.因此为进一步提高脉冲星时间尺度的稳定度和准确度,还需要引进更精确的Timing噪声模型、更好的观测设备以及更长的观测数据序列,这将是脉冲星时间尺度后续发展的方向.

分析数据表明有多颗脉冲星的计时残差表现出明显的红噪声特征,目前关于红噪声的产生机制尚不明确,只是在完成脉冲星的各项参数拟合之后,尚残留一些低频的观测噪声[10−11].经过前期的研究可以推断,能够引起红噪声的因素有很多,例如,观测采用的地球质心历表误差、TT与TCB(Barycentric Coordinate Time)之间转换时所采用的理论表达式的参数误差、脉冲星自身的物理机制,以及某些常数采用值误差等,均是计时残差中红噪声的成因.在后续的工作中,我们计划对拟合模型进行进一步优化,逐步剥离红噪声中的系统性组成部分,通过对红噪声的分析和解析,可以提高各项参数的拟合精度.

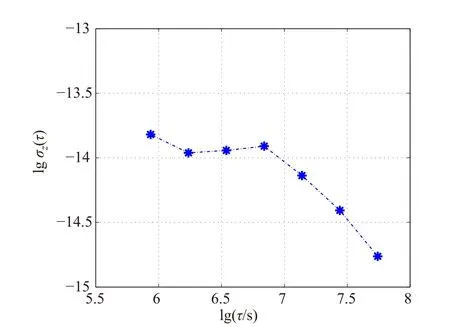
图7 综合脉冲星时间尺度的频率稳定度Fig.7 The frequency stability of the ensemble pulsar time scale

5 结语

由于受到各脉冲星的观测数据采样时间非等间隔、总观测时间跨度不同和多种噪声源等因素的影响,降低了由单颗脉冲星产生的脉冲星时间尺度的稳定度和准确度.为消除这些因素的影响,本文提出了综合脉冲星时间尺度的新算法,并利用实测数据进行试验验证.试验结果表明新的脉冲星时间尺度可有效降低脉冲星时间残差中的噪声影响,并提高了综合脉冲星时间尺度的长期稳定度.

致谢感谢美国国立射电天文台Scott Ranson以及Paul Demorest在观测数据方面所提供的帮助.

[1]仲崇霞.综合脉冲星时算法及脉冲星时应用.西安:中国科学院国家授时中心,2007

[2]Hobbs G,Coles W,Machester R N,et al.MNRAS,2012,427:2780

[3]Vondrak J.BAICz,1977,28:84

[4]Arzoumanian Z,Brazier A,Burke-spolaor S,et al.ApJ,2015,813:65

[5]Hobbs G,Edwards R T,Manchester R N,et al.MNRAS,2006,369:655

[6]Hobbs G,Jenet F,Lee K J,et al.MNRAS,2009,394:1945

[7]Edwards R T,Hobbs G,Manchester R N.MNRAS,2006,372:1549

[8]Hobbs G,Archibald A,Arzoumanian Z,et al.CQGra,2010,27:2006

[9]Riley W J.Handbook of Frequency Stability Analysis.Washington:U.S.Government printing office, 2008

[10]杨廷高,高玉平,童明雷,等.天文学报,2015,56:370

[11]Yang T G,Gao Y P,Tong M L,et al.ChA&A,2016,40:256

Ensemble Pulsar Time Scale

YIN Dong-shan1,2,3GAO Yu-ping1,2ZHAO Shu-hong1,2
((1 National Time Service Centre,Chinese Academy of Sciences,Xi’an 710600)
(2 Key Laboratory of Time and Frequency Primary Standards,National Time Service Center,Chinese Academy of Sciences,Xi’an 710600)
(3 University of Chinese Academy of Sciences,Beijing 100049)

Millisecond pulsars can generate another type of time scale that is totally independent of the atomic time scale,because the physical mechanisms of the pulsar time scale and the atomic time scale are quite di ff erent from each other.Usually the pulsar timing observational data are not evenly sampled,and the internals between data points range from several hours to more than half a month.What’s more,these data sets are sparse.And all these make it difficult to generate an ensemble pulsar time scale. Hence,a new algorithm to calculate the ensemble pulsar time scale is proposed.Firstly, we use cubic spline interpolation to densify the data set,and make the intervals between data points even.Then,we employ the Vondrak filter to smooth the data set,and get rid of high-frequency noise, finally adopt the weighted average method to generate the ensemble pulsar time scale.The pulsar timing residuals represent clock di ff erence between the pulsar time and atomic time,and the high precision pulsar timing data mean the clock di ff erence measurement between the pulsar time and atomic time with a high signal to noise ratio,which is fundamental to generate pulsar time.We use the latest released NANOGRAV(North American Nanohertz Observatory for Gravitational Waves)9-year data set to generate the ensemble pulsar time scale.This data set is from the newest NANOGRAV data release,which includes 9-year observational data of 37 millisecond pulsars using the 100-meter Green Bank telescope and 305-meter Arecibo telescope.We find that the algorithm used in this paper can lower the in fl uence caused by noises in timing residuals,and improve long-term stability of pulsar time.Results show that the long-term(>1 yr)frequency stability of the pulsar time is better than 3.4×10−15.

time,pulsars,methods:observational,data analysis

P127

:A

10.15940/j.cnki.0001-5245.2016.03.008

2015-10-26收到原稿,2015-12-21收到修改稿

∗国家自然科学基金项目(11303032,11473029)及地理信息工程国家重点实验室开放基金课题(SKLGIE2013-M-1-1)资助

†yds@ntsc.ac.cn