暗物质粒子探测器径迹重建方法的研究∗

鲁同所雷仕俊藏京京常 进伍 健

(1中国科学院紫金山天文台南京210008)

(2中国科学院暗物质与空间天文重点实验室南京210008)

(3中国科学院大学北京100049)

暗物质粒子探测器径迹重建方法的研究∗

鲁同所1,2,3†雷仕俊1,2‡藏京京1,2常 进1,2伍 健1,2

(1中国科学院紫金山天文台南京210008)

(2中国科学院暗物质与空间天文重点实验室南京210008)

(3中国科学院大学北京100049)

暗物质粒子探测器(DAMPE,Dark Matter Particle Explorer)旨在通过对空间高能粒子的大能量范围、高能量分辨和高空间分辨的观测间接探究暗物质的存在和分布.径迹重建是利用探测器不同位置探测通道的观测结果重建高能粒子入射位置和方向,其结果的准确性决定了探测器的空间分辨本领.暗物质粒子探测器径迹重建主要依靠其中的硅阵列探测器(STK,Silicon Tracker)和BGO(锗酸铋,Bi4Ge3O12)量能器两个子探测器的观测.结合两者的设计原理和结构,利用多次束流试验和地面宇宙线实验数据细致探讨了径迹重建的基本方法,主要包含3个基本步骤:径迹点的选取,径迹点的拟合以及最佳径迹的判选.粒子在每层STK和BGO晶体中往往留下多个击中点,首先给出了一种利用BGO重心法得到粒子粗略径迹并以此限定STK径迹点的方法.接着对于选定的一组可能的STK径迹点尝试了Kalman滤波和直线最小二乘拟合两种拟合法,并发现两种方法分别独立得到比较一致的结果,从而验证了结果的有效性.最后,对于重建得到的多条可能径迹,讨论了一些利用BGO量能器和STK结果进行联合判选的方法.利用提出的径迹重建方法对多次束流试验数据的处理表明,暗物质粒子探测器的空间分辨完全达到了设计要求.

仪器:探测器,行星和卫星:探测,伽马射线:星际介质,宇宙学:暗物质,方法:数据分析

1 引言

有关暗物质的问题是困扰天文学和现代物理学发展的一大难题,目前对暗物质的探测正处在高速发展阶段.在中国,以暗物质为目标的暗物质粒子探测器于2015年12月17日发射升空,它采用的是大纵深、三维全吸收型的量能器,具有测量能量范围大、能量分辨率高和本底抑制能力强等优势.根据物理设计的要求和模拟的结果,暗物质粒子探测器由4个子探测器组成,从顶层到底层分别为:塑料闪烁体探测器(PSD,Plastic Scintillator Detector)、硅阵列探测器、BGO量能器和中子探测器(NUD,Neutron Detector).如图1所示.

塑闪阵列探测器分系统有效探测面积为820 mm×820 mm,整个分系统由两层共82个X、Y方向互相垂直放置的塑闪单元模块组成,其中78个塑闪单元模块的尺寸为884 mm×28 mm×10 mm,另外4个塑闪单元模块的尺寸为884 mm×25 mm×10 mm.塑闪阵列探测器探测单元的两端采用光电倍增管将光信号转换为电信号再进一步处理.

硅阵列探测器有6大层,每个大层由相互垂直的分别沿X、Y方向的两层硅微条探测器构成,主要用于测量入射粒子的方向和径迹.在第二、第三和第四大层上方各设置了一层1.0 mm厚的钨板,用来将伽马光子转换为正负电子.考虑到光子转换后,需测量产生的次级粒子径迹,为实现粒子电荷的区分,特别是区分伽马光子和电子[1],钨板下方应有多层硅微条探测器[2].

BGO探测器主体由308根BGO晶体构成,如图2所示,其探测面积为60 cm×60 cm. BGO探测器共分为7大层,每大层由X、Y两小层构成.每小层22个探测单元,由22根晶体排列组成,每个探测单元(BGO晶体)的尺寸为2.5 cm×2.5 cm×60 cm.BGO探测器探测单元的两端采用1个R5610A-01光电倍增管(PMT)将光信号转换为电信号[3−6].

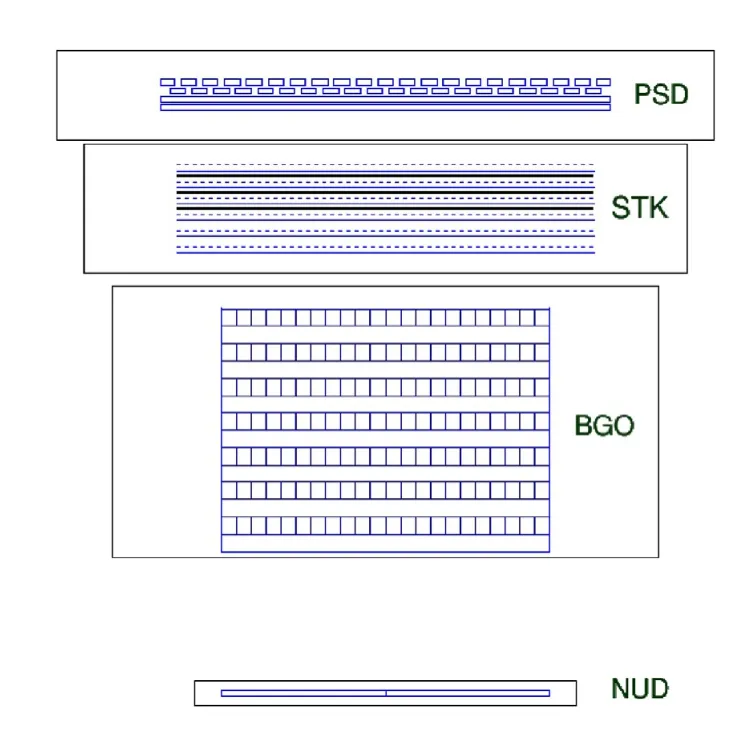
图1 子探测器概念图Fig.1 A sketch of 4 sub-detectors

图2 BGO量能器位置示意图Fig.2 The detailed geometry of BGO calorimeter

中子探测器位于暗物质粒子探测器底层,采用厚度为1 cm、掺硼(B)的塑料闪烁体探测器(Saint Gobian公司生产的BC454).探测器由外形轮廓693 mm×693 mm的塑料闪烁体分割成4个独立的正方形,并各自去除一个角以耦合一个PMT读出构成一个完整的探测平面.它是为测量宇宙线中的强子(主要为质子)与中子探测器上层的物质发生作用产生的次级粒子而设计的,根据这些中子在探测器内的能量沉积,可以判断入射粒子的类型,配合BGO量能器进一步区分质子和电子[7−8].

2 径迹重建的流程

考虑探测器的几何构型和精度,为了近似描述粒子的数学模型,我们在径迹拟合中采用的方法如图3所示.

图3 径迹重建拟合的流程图Fig.3 A fitting fl ow diagram for reconstructing the incident particle trajectory

3 BGO量能器中粒子的径迹重建

BGO量能器中的径迹重建思路如下:当入射粒子通过量能器时,由于粒子与介质原子的相互作用(主要是电磁相互作用和强相互作用),入射粒子把能量沉积在量能器中,根据簇射形状,我们大致可以判断出径迹方向.具体实现如下:首先是BGO层的选取,设定一个能量阈值以排除背景噪声,根据多次统计结果,初步设定2%,也就是当每层BGO的能量占总能量超过2%时,该层才作为参考层,参与BGO的径迹重建.其次,选取每一层中参与径迹重建的BGO晶体,我们选取每层中能量沉积最高的晶体及左右两侧各一根共3根晶体计算该层能量沉积的重心,详见(1)式.如果其中一层中,能量沉积最高的晶体恰好位于边缘,也就是左侧或者右侧没有晶体,为了减小误差,我们只选取这根能量最高的晶体参与重建;如果其中一层中,能量沉积最高的晶体不在边缘,但是其左侧和右侧的晶体能量相差很大,也就是一侧的能量相对于另一侧基本忽略不计,我们依然选取能量较高的2根晶体参与重建,因为当粒子同时穿过相邻的2根晶体,接着从下方穿出的这种情况是可能存在的.然后做直线拟合:采用的是能量加权的线性拟合,用于加权的能量为参与重建的晶体能量之和.(1)式中,xc、xmax、Emax分别表示BGO量能器某层的能量重心位置、该层能量最大的那根晶体的位置和能量.xmax−1、xmax+1、Emax−1、Emax+1分别表示xmax左、右两侧晶体的位置和能量.

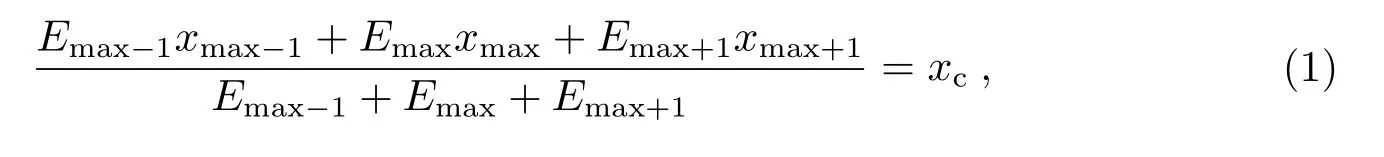
图4为垂直入射400 GeV的质子径迹重建效果.该图为XZ平面的投影图,图形右侧几排点为量能器中实际击中的BGO晶体的能量重心位置,每个点横向误差棒长度表示沉积能量大小,直线为拟合的粒子径迹.图中(X<0)6个点是STK的团簇(cluster).

图4 从暗物质粒子探测器顶部垂直入射的400 GeV的质子径迹重建效果Fig.4A reconstructed particle event display.The particle is a proton with a momentum of 400 GeV vertically impacting on the top surface of DAMPE.

4 硅阵列探测器(STK)的径迹重建

4.1 Cluster的选取

BGO晶体尺寸比较大,为2.5 cm×2.5 cm×60 cm,所以在重建过程难免会存在一定的误差,这是系统本身造成的,我们可以利用这个误差范围来限制硅探测器团簇的选取.

图5为利用BGO量能器信息重建出的粒子径迹方向的分布图,在STK径迹重建过程中选取团簇时可以给出参考.左上图表示BGO中粒子径迹在XZ平面内的投影与Z轴的夹角θx随事例累计的分布情况;右下图表示BGO中粒子径迹在Y Z平面内的投影与Z轴的夹角θy随事例累计的分布情况;左下图横坐标表示粒子径迹在XZ平面内的投影与Z轴的夹角θx,纵坐标表示径迹在Y Z平面内的投影与Z轴的夹角θy.右上图表示粒子径迹与Z轴方向的夹角θ随事例累计的分布情况.

根据测算,为减小偏差,硅探测器中重建的径迹斜率(倾角)取偏离BGO中重建的径迹斜率(倾角)±5◦,从图5我们可以清楚地看出,5◦以内基本包含了绝大多数的击中点,截距取±25 mm(一根BGO晶体的厚度),也就是限定这样一个范围在硅探测器中寻找径迹.假定BGO重建的径迹在XZ平面的投影方程为lc:z=ax+b,如图6所示.则限定团簇选取范围的直线方程为:

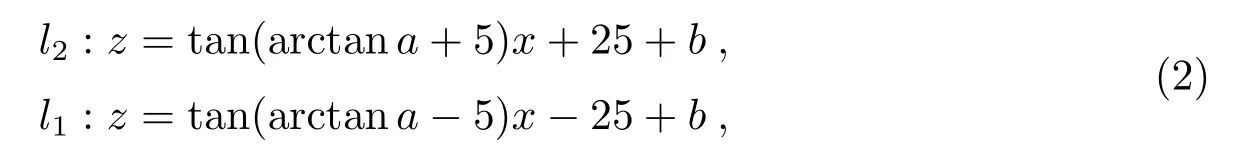
其中a、b分别表示投影方程的斜率和截距.

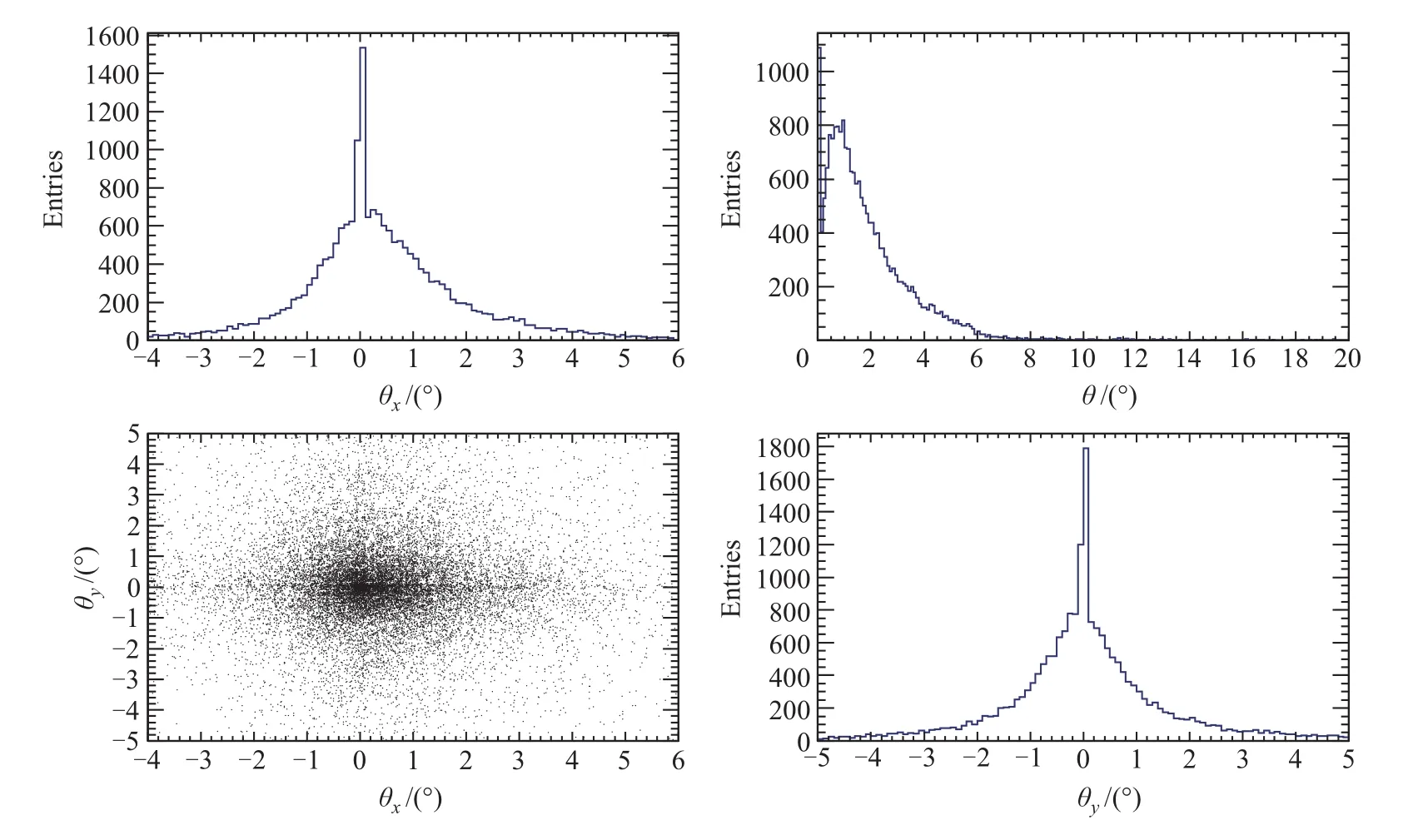
图5 BGO中径迹方向分布图Fig.5 The track reconstruction performance of BGO calorimeter

4.2 寻迹

寻迹是一种模式识别过程,属于人工智能的范畴[9−10],它的任务是把一组实验测量点分成两类:第1类可分为许多子类,每个子类中的点都是由同一个粒子引起,即对应于同一径迹;第2类则是在充分可信的程度下无法划分给任何粒子的那些点,即噪声.

目前径迹识别的方法有两类,即所谓的局域方法和全局方法.局域方法中一次只选择一条候选径迹,典型的做法是从少数几个点开始(候选径迹初始化),然后对属于该候选径迹的点进行预测,例如基于已经找出的候选径迹按照当前使用的径迹模型进行内插或者外延来预测径迹的其他击中点.如果找到了额外的点,就将它们加入到候选径迹中去,否则,经过一定次数的尝试以后(尝试次数取决于算法所容许的探测器的探测失效程度),该候选径迹被丢弃.为了寻找候选径迹,局域方法总是必须进行无结果的尝试,于是在不同的组合中会用到同一个点,因此随着点数的增加,计算时间的增加速率远高于线性增加的速率.如果所有的对象(击中点)以相同的方式出现在算法之中,则称为全局方法.这一算法产生一个径迹表,利用它能够更容易地从原始数据中找出径迹,该算法可以被视为一种事例坐标或者空间点的全部数据集的一般的变换.全局方法的计算用时原则上应当正比于一个事例中的击中点数.

具体到该探测器,当高能电子进入硅微条探测器会发生电离损失,损失很小的能量,但由于硅阵列探测器中共有3 mm厚度的钨板,所以很大一部分电子在钨板中会开始发生电磁簇射[11−12],产生更多的电子,转换为电信号后被探测到.或者在接下来几层硅微条中会产生很多团簇,当然也可能存在反散射粒子与上一层硅微条作用产生的团簇,但相比电磁簇射要小得多.我们选择团簇的重心位置作为我们处理数据过程中的一个点.高能质子进入硅微条探测器中,主要发生电离损失,由于钨板厚度虽小,但密度较大,也有可能会发生少量的强子簇射,但是概率比较小[13].

根据以上物理原理,结合限定条件,遍历寻找所有可能的径迹.其中一种方法为:遍历过程中,在限定的范围内,我们任意选取2个点去拟合一条直线,然后判断其他层上是否有靠近该直线的点(依据是:如图6,如果点到直线ls的距离小于1 mm,我们就认为该点靠近直线),找出靠近直线的点最多,并且方差σ2最小的那条直线,然后利用该直线上的点和靠近直线的点,重新拟合直线,那么重新拟合后的直线就是我们要寻找的硅微条探测器中重建的径迹.为了减少计算量、提高准确度,最终我们选取的候选径迹至少包含3个点,因为理想情况下应该有6个点,即便有一个坏点,还有5个点可以参与拟合,如果选取3个以下的点,尽管有2个点便可以构成一条直线,但是这种情况出现的概率比较小,几乎可以忽略不计.

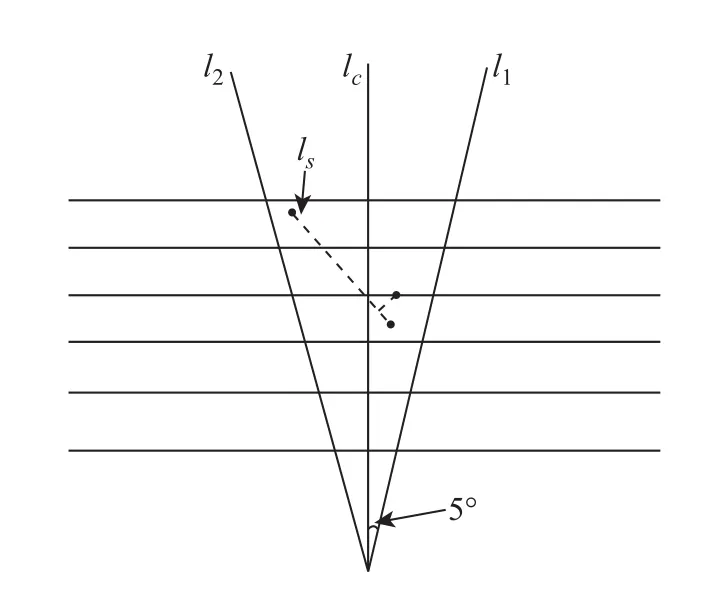
图6 团簇的寻找范围Fig.6 The geometric range for searching the cluster

在寻迹过程中主要考虑以下两点:一是径迹要尽可能长、尽可能是一条直线,通俗地讲就是选取的点尽可能多,方差尽可能小.二是要与BGO径迹的方向最匹配,尽可能一致,也就是斜率和截距尽可能接近,但是实际处理过程中,比对斜率和截距的方式是比较困难的.我们采取一种更加合理、方便的方法,如图7所示,图中两条直线分别表示利用BGO信息重建拟合的径迹和利用硅微条信息并且遍历所有可能点后得到的一条可能的径迹,它们与硅微条的交点分别为X1,X2,···,X6和X′1,X′2,···,X′6.我们很容易得到:

越小时,这两条直线越靠近.也就是当它最小时,基本上认为两条直线最匹配.另外一种方法:因为任意两点即可确定一条直线,我们在限定的范围内任意选取2点拟合一条直线,排除偏离利用BGO重建的径迹5◦以上的直线,如图5所示,因为5◦以内基本包含了绝大多数的点(可能的径迹).然后判断其他层上是否有靠近该直线的点,找出靠近直线的点最多并且χ2最小的直线,再利用该条直线上的点和靠近直线的点重新拟合直线,那么,新拟合出的直线就是我们要寻找的硅微条探测器中重建的径迹.

图7 硅阵列探测器重建的一条可能的径迹在XZ平面内的投影Fig.7 A projected line of track candidate in XZ plane reconstructed with STK

4.3 径迹拟合

4.3.1 带有能量加权的最小二乘法直线拟合

已知数据测量点(xi,yi)(i=1,2,···,n),能量加权就是令xi=Exixi,yi=Eyiyi,拟合y=b′′+a′′x,求出a′′、b′′:

其中Exi、Eyi分别表示第xi和第yi个团簇或者晶体对应的能量值,a′′和b′′分别表示直线的斜率和截距.

重建的结果如图8和图9.图8表示30◦方向入射的100 GeV的电子径迹重建结果,其中实线是BGO重心法拟合的结果,虚线为BGO给出的限制,点划线为硅阵列探测器中粒子径迹的最佳拟合结果,这是在XZ平面的投影图,横坐标表示沿Z轴方向各个击中的重心位置,纵坐标表示沿X方向各个击中点的重心位置.图9显示的是0◦方向入射的400 GeV的质子径迹重建效果.

图10能很好地检验重建效果,左上图表示BGO中粒子径迹在XZ平面内的投影与Z轴的夹角θx随事例累计的分布情况;右下图表示BGO中粒子径迹在Y Z平面内的投影与Z轴的夹角θy随事例累计的分布情况;左下图横坐标表示粒子径迹在XZ平面内的投影与Z轴的夹角θx,纵坐标表示径迹在Y Z平面内的投影与Z轴的夹角θy.右上图表示粒子径迹与Z轴方向的夹角θ随事例累计的分布情况.图中对于垂直入射的粒子,理想的重建结果角度分布的中心位置应该在0◦,但是对于图9 0◦入射400 GeV质子的重建结果, Y方向基本在零点位置,而X方向偏离中心零点0.35◦左右,这可能有两方面的原因:(1)由于探测器安装偏差及仪器测量等系统性问题,造成粒子可能不是精确的0◦入射.(2)可能是我们的算法还有待完善,没能找出真实的径迹.从左上角和右下角的图形中我们可以看出,在偏离中心位置的还有尾巴,这些基本是重建出的假径迹,我们还没能将其全部排除.左下角的图形也能清楚地看出偏离中心位置还存在一些散点.

图8 硅微条探测器与BGO量能器联合重建的结果(100 GeV电子,30◦方向入射)Fig.8A trajectory of an electron with a momentum of 100 GeV and an incident angle of 30◦.The track is the reconstructed result jointly using BGO and STK.

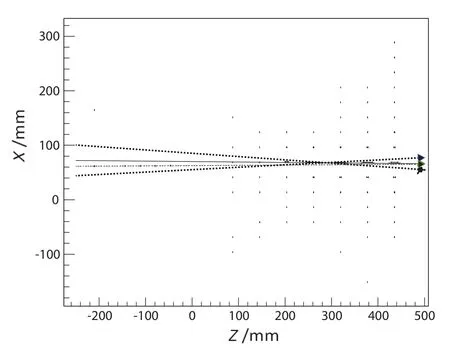
图9 硅微条探测器与BGO量能器联合重建的结果(400 GeV质子,0◦方向入射)Fig.9 A trajectory of a proton with a momentum of 400 GeV and an incident angle of 0◦.The track is the reconstructed result jointly using BGO and STK.

4.3.2 基于卡尔曼滤波的直线拟合

卡尔曼滤波是匈牙利数学家Rudof Email Kalman在1960年首先提出的一种线形滤波与预测问题的方法[14].在直线拟合过程中,经常用到最小二乘法[15−16],对于有伪点的线性拟合,由于部分伪点与拟合直线偏差大,出现了拟合径迹偏离真实径迹的现象,有些伪点的出现是由人为造成的,这种情况可将伪点剔除再进行拟合.但是根据经验或者直觉将伪点剔除,此种做法缺乏说服力,所以要通过有效方法去判断.卡尔曼滤波是一种统计估算方法,由于其具有最小无偏方差性,能够去除实验中的随机误差来获取更接近真实值的信息,目前被广泛应用于各领域.对于解决大部分的问题来说,它是一种最有用、效率最高的算法.

图10 硅微条探测器中的径迹方向分布图Fig.10 The track reconstruction performance of the Silicon Tracker Detector

图11和图12为宇宙射线µ子击中探测器后,利用带有能量加权的最小二乘法和卡尔曼滤波分别处理后得到径迹的斜率和截距的散点分布图,其中图11的横坐标表示利用带有能量加权的最小二乘法直线拟合后得到的径迹的斜率(倾角),单位为度;纵坐标表示通过卡尔曼滤波处理后得到的径迹的斜率(倾角),单位为度;图12的横坐标表示利用带有能量加权的最小二乘法直线拟合后得到的径迹的截距,单位为mm;纵坐标表示通过卡尔曼滤波处理后得到的径迹的截距,单位为mm.从图11∼12中,我们可以清楚地看出,两者斜率和截距的分布比较集中,大致都在斜率为1的直线型区域,说明:基于卡尔曼滤波的直线拟合和带有能量加权的最小二乘法重建效果大体相当,基本差别不算太大.

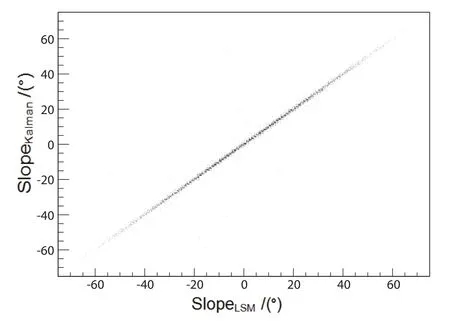
图11 两种方法拟合得到的斜率(倾角)的散点图Fig.11 A scattered plot of the slopes(inclinations) fitted with two methods

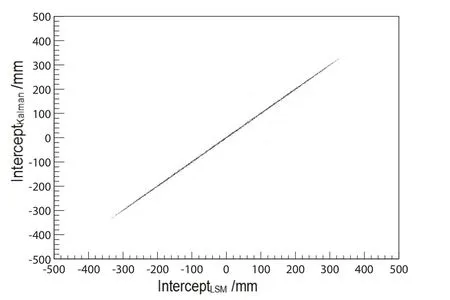
图12 两种方法拟合得到的截距散点图Fig.12 A scattered plot of the intercepts fitted with two methods

在0◦入射的100 GeV电子和400 GeV的质子击中探测器后产生的数据中随机选取两个事例,经过带有能量加权的最小二乘法与卡尔曼滤波方法处理后的径迹拟合参数比较如表1.

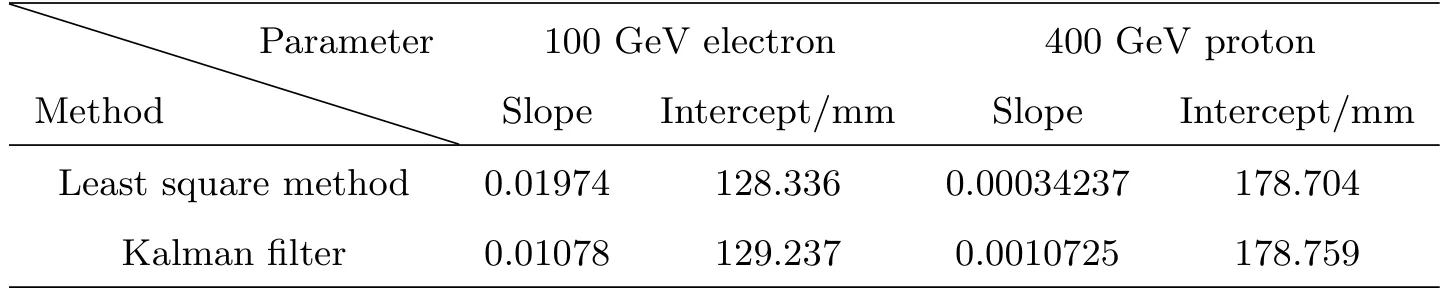
表1 径迹拟合参数Table 1 The parameters of track fitting

重建结果如图13和图14所示.图13和图14中,实线是利用卡尔曼滤波法重建的径迹,点线是带有能量加权的最小二乘法直线拟合的结果,虚线是利用BGO量能器簇射情况重建的结果,黑色点为击中探测器的位置.我们统计了多个能量段的径迹重建结果后发现:对于低能区,基于卡尔曼滤波的拟合结果要比最小二乘法有明显的优势,如图13,实线与点线并不重合,且实线更加接近于真实的径迹.对于高能区,带有能量加权的最小二乘法与卡尔曼滤波结果差别不大,如图14,实线与点线基本重合,经过探测器位置标定后,基本都接近于真实的径迹.

5 误差分析

造成重建结果误差的因素有很多,我们对最主要的几个可能做一下介绍:

(1)束流试验中,探测器位置本身就是粗略的,并不是很精确,或者说探测器某个部件可能会偏离中心位置,而且偏离方向还可能不太一致,这可能会影响我们对坐标系的选取,造成探测器某一个部件到坐标轴或者坐标原点的计算出现误差.这要求我们处理数据之前进行位置校正,确保在同一个坐标系下进行.

(2)由于探测器本身材料的问题,当粒子击中探测器后,可能会产生很多次级粒子,比如多重散射,包含带电粒子,我们无法判断团簇是由哪些粒子造成的.当然也可能有反冲粒子与探测器作用产生的团簇.

(3)我们处理数据时选取的击中点是团簇的重心位置,但是粒子实际击中探测器的位置不一定就是重心位置,可能有偏差.

图13 0◦入射的100 GeV电子径迹重建的结果Fig.13A reconstructed trajectory of electron with a momentum of 100 GeV and an incident angle of 0◦

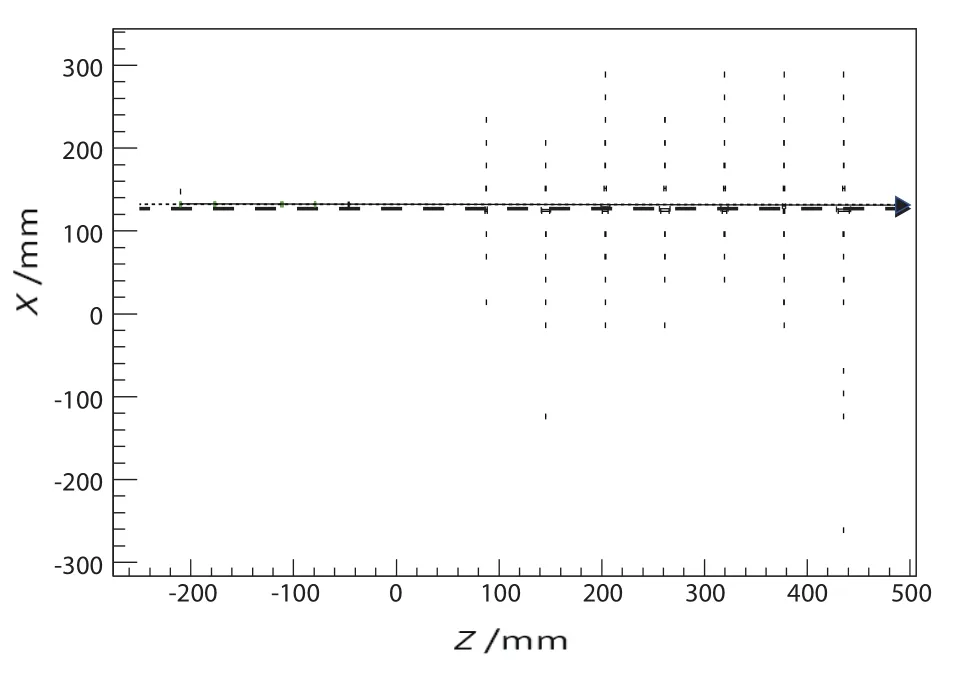
图14 0◦入射的400 GeV质子径迹重建的结果Fig.14 A reconstructed trajectory of proton with a momentum of 400 GeV and an incident angle of 0◦

6 总结

径迹重建在暗物质粒子探测方面有着很重要的意义,再现入射粒子径迹,有助于得到入射粒子的种类、能量、强度、入射方向等相关信息,进而判断分析入射粒子的产生以及源的方向.如果这些粒子是由暗物质衰变或者湮灭产生的,还可以了解暗物质的分布情况及与其他物质分布的相关性.径迹重建最重要的几点是:伪点的剔除、寻迹、径迹拟合和相关的修正.过程中要考虑几个关键问题,比如:探测器性能(主要是几何构形和精度(分辨)),还有能量损失、多重散射等等,然后以足够好的精度构建一个近似描述粒子轨迹的数学模型.为了验证模型和算法的准确性,在对真实的实验数据进行分析之前,整个重建链过程应当利用模拟数据进行测试,模拟数据中所估计的参数的真值应当是已知的,以便能够对归一化残差进行检查.拟合参数的精确误差应当加以仔细研究,它们可能受到伪点或者伪径迹及其去除方法的影响,以及探测器位置安装偏差的影响.

本文主要采用能量加权的最小二乘法和基于卡尔曼滤波的直线拟合方法重建入射粒子径迹,通过对比,重建径迹的效果(误差)跟入射粒子能量大小存在一定关系.大体上说,入射能量越高,重建结果误差可能会越小.另外我们发现:在高能区利用加权的最小二乘法直线拟合与卡尔曼滤波经过预测、过滤、平滑得到的结果基本没有太大差别,但是在低能区,卡尔曼滤波还是拥有比较明显的优势.卡尔曼滤波是一种强有力、灵活和有效的工具,它不仅仅适用于径迹拟合,还适用于最优外延和内插的计算、伪点的搜索和排除、利用真实的数据进行误差调整和探测器校准以及径迹段的合并.但是卡尔曼滤波也有自身的缺陷,有时候很难找到卡尔曼滤波的一个适当的初始值,如果初始探测器的角度分辨和动量分辨很差,并且与下一个探测器不是很靠近,第1次的预测步骤会存在以下问题:

(1)很难准确计算粒子真实轨迹穿过的物质量,因为预测的路径可能与实际路径完全不符.

(2)如果初始值偏离真实径迹过远,径迹模型的线性近似将会无效.

(3)当预测的路径与下一个探测器表面不相交,预测步骤将无法进行.

对于这种问题的一个解决方法是将模式识别方法求得的参考径迹取为线性近似展开点.首先计算参考径迹与所有表面的交点(称为参考状态),然后利用状态和参考状态的差值进行预测、滤波和平滑化运算.

此外,仪器在放置时位置测量并不是完全精确的,仪器的标定对径迹重建的结果也会产生一定的影响,因此,为提高径迹重建的效果,对仪器进行校准也是有必要的.

[1]Chang J.ChJSS,2014,34:550

[2]董亦凡.暗物质粒子探测卫星硅探测器数据获取系统的研究.北京:中国科学院高能物理研究所,2015

[3]张云龙.空间暗物质探测电磁量能器的研究.合肥:中国科学技术大学,2011

[4]谢明刚,郭建华,伍健,等.天文学报,2014,55:170

[5]Xie M G,Guo J H,Wu J,et al.ChA&A,2015,39:129

[6]郭建华,蔡明生,胡一明,等.天文学报,2012,53:72

[7]张磊,郭建华,张永强.天文学报,2014,55:522

[8]Zhang L,Guo J H,Zhang Y Q.ChA&A,2015,39:380

[9]Fruhwirth R,Regle M.高能物理数据分析.朱永生,译.合肥:中国科学技术大学出版社,2011

[10]刘靖,毛泽普,李卫国,等.高能物理与核物理,1998,22:587

[11]汪晓莲.粒子探测技术.合肥:中国科学技术大学,2009

[12]Mao Z P,Wang T J,Wang S Q.HEPNP,1993,17:193

[13]Grupen C,Shwartz B,Spieler H.Particle Detectors.Cambridge:Cambridge University Press,2011

[14]Kalman R E.Transactions of the ASME-Journal of Basic Engineering,1960:35

[15]王江荣.自动化与仪器仪表,2013:140

[16]高飞,童恒庆.系统工程与电子技术,2006,28:775

Researches on Track Reconstruction for DAMPE

LU Tong-suo1,2,3LEI Shi-jun1,2ZANG Jing-jing1,2Chang Jin1,2WU Jian1,2
(1 Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008)
(2 Key Laboratory of Dark Matter and Space Astronomy,Chinese Academy of Sciences,Nanjing 210008)
(3 University of Chinese Academy of Sciences,Beijing 100049)

The Dark Matter Particle Explorer(DAMPE)is aimed to study the existence and distribution of dark matter via observation of high energy particles in space with unprecedented large energy bandwidth,high energy resolution,and high space resolution.The track reconstruction is to restore the positions and angles of the incident particles using the multiple observations of di ff erent channels at di ff erent positions, and its accuracy determines the angular resolution of the detector.The track reconstruction is mainly based on the observations of two sub-detectors,namely,the Silicon Tracker(STK)detector and the BGO(Bi4Ge3O12)calorimeter.In accordance with the design and structure of the two sub-detectors and using the data collected during the beam tests and ground tests,we provide a detailed introduction of the track reconstruction of DAMPE data,including three basic steps,the selection of track hits, the fitting of track hits,and the judgement of the best track among(most probably) many of them.Since a high energy particle most probably leaves more than one hit in each level of the STK and BGO,we first provide a method to constrain the STK clusters for the track reconstruction using the rough result of the BGO reconstruction. We apply two di ff erent algorithms,the Kalman filter and the least square linear fitting, to fit the track hits.The consistency of the results obtained independently via the two algorithms con firms the validity of our track reconstruction results,and we discuss the advantages/disadvantages of each method.Several criteria combining the BGO and STK detection are discussed for picking out the most possible track among all the tracks found in the track reconstruction.Using the track reconstruction methods mentioned in this article and the beam test data,we con firm that the angular resolution of DAMPE satis fies the requirement in design.

instrumentation:detectors,planets and satellites:detection,gamma rays: ISM,cosmology:dark matter,methods:data analysis

P111

:A

10.15940/j.cnki.0001-5245.2016.03.011

2015-10-16收到原稿,2015-11-16收到修改稿

∗国家自然科学基金项目(11303105、11303106、11303107)资助

†tslu@pmo.ac.cn

‡sjlei@pmo.ac.cn