基于堆叠降噪自编码的恒星/星系分类研究∗

秦浩然林基明王俊义

(1桂林电子科技大学广西信息科学实验中心桂林541004)

(2桂林电子科技大学广西密码学与信息安全重点实验室桂林541004)

基于堆叠降噪自编码的恒星/星系分类研究∗

秦浩然1†林基明1‡王俊义2

(1桂林电子科技大学广西信息科学实验中心桂林541004)

(2桂林电子科技大学广西密码学与信息安全重点实验室桂林541004)

近年来,深度学习算法以其适应性强、准确率高、结构复杂等特性在数据挖掘算法中异军突起,但是在天文信息学中深度学习算法还鲜有问津.针对斯隆数字巡天(Sloan Digital Sky Survey,SDSS)恒星/星系分类中普遍存在的亮源集分类正确率高但暗源集分类正确率低等问题,引入了深度学习中较新的研究成果—堆叠降噪自编码(stacked denoising autoencoders,SDA)神经网络和dropout微调技术.从SDSS释放出的带有光谱证认(spectroscopic measurements)的测光数据中分别随机抽取DR7(Data Release 7)和DR12(Data Release 12)的亮源集和暗源集并对其进行预处理,再分别对它们的亮源集和暗源集做不放回随机抽样,得到它们亮源和暗源的训练集和测试集.最后用这些训练集分别训练得到了DR7和DR12亮源和暗源的SDA模型,并将SDA在DR12测试集上的测试结果与支持向量机软件包(Library for Support Vector Machines,LibSVM)、J48决策树(J48)、逻辑模型树(Logistic Model Trees,LMT)、支持向量机(Support Vector Machine,SVM)、逻辑回归(Logistic Regression)、单层决策树算法(Decision Stump)上的测试结果进行比较,同时将SDA在DR7测试集上的测试结果与6种决策树的测试结果进行比较.仿真表明SDA在SDSS-DR7和最新SDSS-DR12的暗源集上的分类性能明显优于其他算法,尤其是在使用完备函数(completeness function,CP)作为衡量指标时,SDA相比决策树算法在SDSS-DR7暗源集正确率提高了15%左右.

方法:数据分析,技术:测光,星系:基本参数,恒星:基本参数,宇宙学:观测

1 引言

在过去30多年中,随着先进数字CCD(Charge-coupled Device)探测器的使用,并结合快速发展的计算力和数据存储技术,天文数据的获取经历了一场革命性的变化,预计每年产生的数据量将可能达到TB级,而面对如此庞大的数据量如何进行有效的数据分析将变得尤为重要.恒星/星系分类是天文数据分析的基本内容之一,人们对它的研究可以追溯到18世纪[1].到目前为止很多方法已经被广泛应用于恒星/星系分类中,它们主要包括了基于形态、启发式分割和机器学习等方法.从形态上区分恒星/星系是一种最普遍的方法[2-5],它们主要是利用恒星与星系所表现出的不同形态(恒星的形态通常为点源,而星系的形态为展源)来进行分类.这些方法对于亮的恒星/星系分类非常有效,原因是从亮源中获得的形态信息的信噪比很高,但是从暗源得到的形态信息包含很大噪声,致使这种方法的效果大大降低.另外一种比较普遍的恒星/星系分类方法是基于可观测图像的属性和相关统计特征进行启发式分割[6-8],这种分类方法的优点是非常容易被定义和仿真,但它也有很多的不足,如分割的选择本质上是带有任意性的.机器学习方法是一类现在非常热门的自动分类方法,主要包括决策树、支持向量机、神经网络和聚类等方法,它们可以有效杜绝启发式分割随意性的问题,如严太生等人将自动聚类算法(Auto Class)应用于恒星/星系分类[9];Vasconcellos等人用13种不同的决策树算法对SDSS数据进行了恒星/星系分类研究,使亮源分类的完备性都达到了99%左右,而暗源分类的完备性为78%左右[10];Malek等人提出一种改进的支持向量机(SVM)的方法并取得了良好的效果[11].但是这些自动算法都存在一些共同问题,比如它们都很难处理样本空间范围之外的恒星/星系数据,即模型的泛化能力不够强,它们对于亮源分类都有着很高的正确率,但对于暗源分类正确率偏低.尽管各种各样的算法被用来解决这个问题,但是由于不同的实验目的(算法速度、自动化程度、单类概率和整体概率等)和信息(形态、颜色、是否使用类标签),直到现在都没有一种公认的有效方法.

本文研究了基于SDA的恒星/星系分类算法,使用SQL(Structured Query Language)从SDSS释放数据集中下载带光谱证认参数(spectroscopic measurements)的测光数据(本文所使用的数据为SDSS-DR7和SDSS-DR12),将得到的数据根据星等值范围不同分别进行不放回随机抽样得到亮源和暗源集,并对抽样得到的数据集进行预处理使其适合于SDA输入.又对暗源集和亮源集做不放回随机抽样分别得到它们的训练集和测试集.最后使用得到的训练集训练SDA模型的众多参数以选择最优,在模型微调阶段加入dropout微调技术来微调整个模型以增加模型的鲁棒性.在对比分析试验中,使用SDSS-DR12亮源和暗源的训练集和测试集分别在支持向量机软件包(Library for Support Vector Machines,LibSVM)、J48决策树(J48)、逻辑模型树(Logistic Model Trees,LMT)、单层决策树算法(Decision Stump)、支持向量机(Support Vector Machine,SVM)、逻辑回归(Logistic Regression)算法上做训练和测试,在使用整体分类正确率作为性能指标的情况下,SDA在暗源集的正确率明显优于其他算法.最后使用SDSS-DR7数据跟Vasconcellos等人使用的决策树算法[10]做比较.使用DR7亮星和暗源的训练集和测试集分别在各种决策树算法上做训练和测试并使用完备函数作为性能指标,结果表明SDA在亮源和暗源集的正确率都优于决策树,特别是暗星正确率提高了15%左右.

2 SDSS数据和恒星/星系分类

SDSS是斯隆数字巡天计划(Sloan Digital Sky Survey)的简称[12].该巡天计划覆盖北天球的一半天区和少部分南天球天区,是迄今为止最大规模的星系图像和光谱巡天项目.SDSS的CCD测光系统利用6组CCD同时对天体进行5个波段(u,g,r,i,z)的测量,5个波段相应的中心波长分别为3551˚A,4686˚A,6165˚A,7481˚A和8931˚A.目前SDSS最新公布的SDSS-DR12,其数据容量超过了100 TB,包含了对近5亿个恒星和星系的精确测光数据,而对其中300多万个恒星/星系数据进行了光谱证认,使得这300多万个恒星/星系数据的天体类别得到了确认.因此,SDSS中包含的精确海量测光数据和光谱数据集,为研究各种恒星/星系分类算法提供了很好的数据支持.

SDSS的天体基本测光参数包括星等、颜色、轮廓、大小等;而光谱基本参数包括红移、光谱型等.其中,光谱数据集分为两种类型:一种是同时带光谱证认参数(spectroscopic measures)和测光参数(photometric measures)数据集,另外一种是只带有测光参数的数据集.SDSS中提供的第1种带光谱证认的测光数据集仅有300多万条,仅占SDSS-DR12测光数据中5亿多个天体数据记录中的极小一部分.如何对没有光谱证认的SDSS测光天体进行分类?本文提出的SDA恒星/星系分类模型可能会是一种有效的方法来解决未知天体类型的分类问题.

3 堆叠降噪自编码

深度学习成为研究热点起始于2006年,当时Hinton和他的学生提出了用深度置信网络(Deep Belief Network,DBN)构建深层结构,并通过逐层地对受限玻尔兹曼机(Restricted Boltzmann Machines,RBM)训练来初始化网络参数,最终在手写数字识别训练集上达到了很好的效果[13].紧接着Bengio等人提出了一种基于自编码构造的深度结构(堆叠自编码,SA)[14].这些方法都是在利用随机梯度下降进行监督学习之前,先对网络参数进行初始化,使其处于最优值附近,这样有效改善了直接计算网络参数带来的遭遇局部较差点的问题.这些方法在对网络每层初始化的时候都用到了非监督的学习方法,尤其是在带标签的数据比较稀少的时候,非监督学习更能发挥较大的作用,堆叠降噪自编码正是在堆叠自编码的基础上发展而来的.

3.1 传统自编码

自编码网络是构成堆叠自编码网络的基础,它可以看作是一个3层的神经网络,由输入层、隐藏层和输出层组成,并分为编码和解码两个阶段.编码阶段:从输入层x到隐藏层y的映射被认为是编码,它一般由非线性函数来实现:

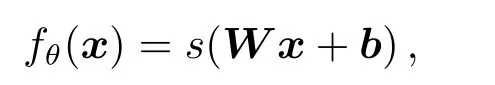
s是一个非线性激活函数,一般为sigm函数、tanh函数和max(0,x)函数.θ={W,b},其中W代表权重矩阵,b代表偏差向量.解码阶段:解码阶段是输出层z通过隐藏层y来重构输入层x的阶段,从隐藏层到输出层的映射称为解码.这个映射为:这里θ′={W′,b′},θ′中的W′和b′可以看作是编码阶段θ中W和b的转置,也可以当做完全不同的参数.值得说明的是,当它们被看作是转置的时候,这里的编码和解码就非常类似于DBN网络的训练过程.

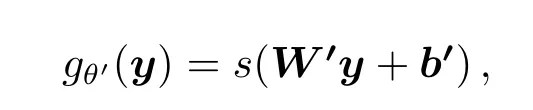
通常z并不被当做是x精确的恢复,而是作为概率项p(X|Z=z)的参数.由此可以得出重组误差L(x,z).根据数据特征,重组误差常采用以下两种形式:

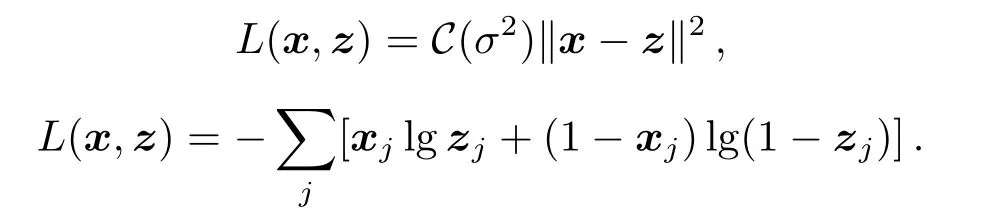
3.2 降噪自编码

从信息论的角度看,最小化重组误差是为了在自编码过程中最大限度地保留输入量x的信息,但是仅仅只保留信息是不够的.如果只为了保留x的信息,设编码映射为y=x将达到最好效果,但显然这是无用的.我们需要的是通过得到有用的特征y来保留输入信息,降噪自编码是一种有效的方法[15],降噪的目的是为了提取更加有用的特征.首先,对原始输入x进行加噪表示为˜x,加噪是通过随机映射产生的,即:˜x∼qD(˜x|x).然后,加噪输入向量˜x通过输入编码被映射到隐藏层,再通过z=gθ(y)得到输出向量.整个过程如图1所示,这里需要特别说明的是这里的输出向量z是尽可能地恢复原始输入向量x而并非˜x.

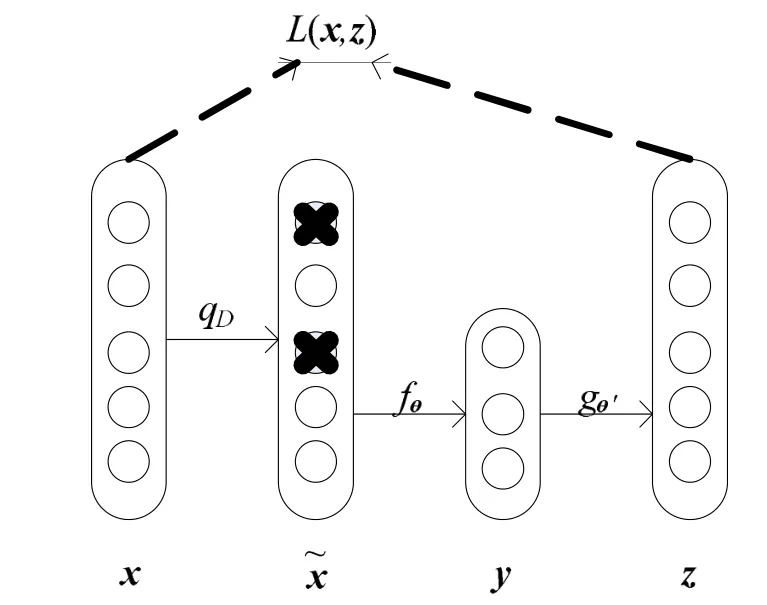
图1 加噪(掩蔽噪声)自编码Fig.1 The corruption(masking noise)autoencoders

3.3 堆叠降噪自编码

用堆叠降噪自编码初始化深度网络类似于在深度置信网络中堆叠受限玻尔兹曼机和传统的堆叠自编码.堆叠降噪自编码的具体过程为:首先,把深层网络的输入层和第1个隐藏层作为降噪自编码的输入和隐藏层进行降噪自编码(如上节所述),用训练后的参数来初始化深层结构中输入层到第1隐藏层的参数,然后再用原始输入向量(不加噪)作为输入前向传播,从而得到了第1层特征向量.接着再把深层网络中第1隐藏层和第2隐藏层作为降噪自编码网络的输入层和隐藏层进行降噪自编码,以此堆叠进行并最终达到对整个深层网络的初始化.需要注意的是输入到下一个降噪自编码输入层的向量是利用输入无噪声向量和之前降噪自编码得到的参数前向传导得到的,图2给出了加噪自编码网络的第1次堆叠过程.

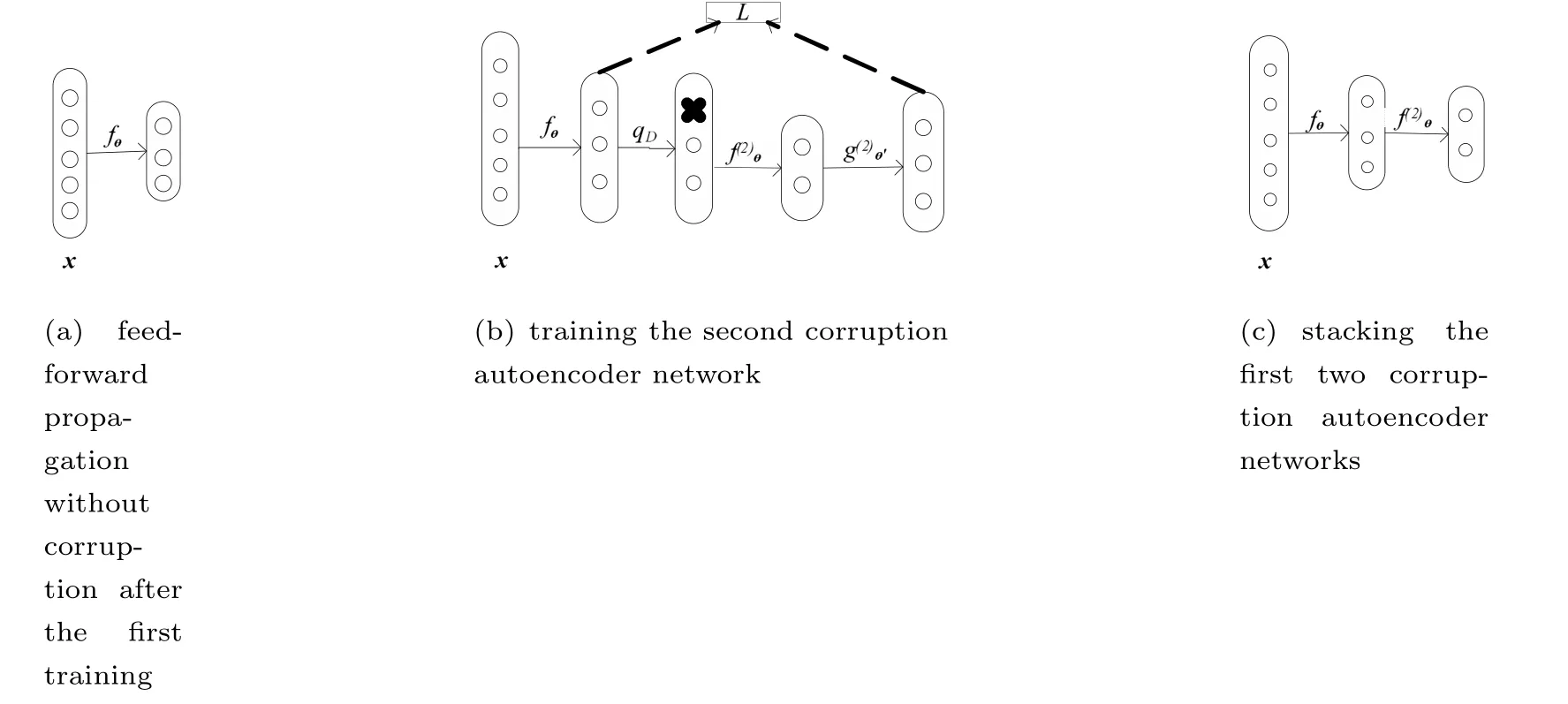
图2 加噪自编码网络第1次堆叠过程Fig.2 The first stacked process of corruption autoencoder network

3.4 微调堆叠降噪自编码网络

当堆叠降噪自编码被建立之后,它的最高层输出可以被用来作为监督学习算法的输入层,例如支持向量机、逻辑回归、softmax分类器等.此时,深度学习算法就可以利用监督学习(一般为随机梯度下降算法)对网络进行参数微调.当对参数微调时,我们不得不面对一个新的问题—模型过拟合.dropout是一个有效解决模型过拟合问题的技术[16],它的关键思想是随机地从一个深层网络中去掉节点(连同与他们连接),这些节点包括了输入层和隐藏层的所有节点.对于每个训练样本以及它们被传到深层网络中的每个节点,dropout都是独立进行的.所以对于有n个节点的深层网络相当于生成了2n个子网络,但全部子网参数是共享的,也就是总的参数并没有改变,注意在测试阶段不需要加入dropout.

4 实验

实验使用SQL查询语言从SDSS巡天获取了所需要的SDSS-DR7和SDSS-DR12测光数据集(见附录1),我们选择了13个SDSS测光参数和1个光谱参数.本文中我们并不讨论在SDSS众多的测量属性中到底哪些属性集可以产生最精确的恒星/星系分类,而是重点选择了那些已知的或者认为与天体分类有密切关联的属性集作为我们算法所需的输入参量集.这些属性主要包括psfMag、 fiberMag、petroMag、petroRad、modelMag、petroR50、petroR90、lnLStar、lnLExp、lnLDeV、mRrCc、mE1和mE2,实验中所用的是r波段数据,详细的描述见参考文献[10].仿真工具我们使用的是matlab工具箱中的深度学习工具箱(Deep Learn Toolbox-master)和WEKA(Waikato Environment for Knowledge Analysis)数据挖掘软件.实验1研究了最新的SDSS-DR12数据,首先去除掉所提取的SDSS-DR12数据中带缺值的数据,再根据属性modelMag等值的不同将其分为两类数据集.具体过程是使用不放回随机抽样的方法抽取modelMag值为14.0–19.0和22.0–22.5之间的数据,把他们分别记为亮源集和暗源集.抽样结果:亮星集包含了4万个恒星和4万个星系数据,暗源集包含5200个恒星和5200个星系数据(SDSSDR12中暗源波段恒星和星系总的数据只有14000条),再对亮源和暗源数据集各属性做归一化预处理.我们再从亮源集中随机抽取10000个恒星和10000个星系作为训练集,余下的作为测试集,从暗源集中随机抽取4000个恒星和4000个星系作为训练集,余下作为测试集.然后比较SDA与其他机器学习算法在测试集上的分类正确率,这些算法包括LibSVM、J48、LMT、Decision Stump、SVM、Logistic Regression.实验1用到的测试指标为测试集中恒星/星系整体分类正确率:

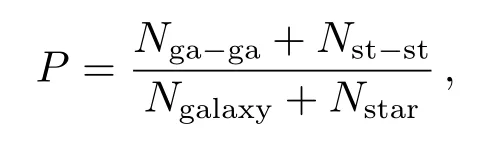
其中Nga−ga表示测试中将测试集中星系分为星系的数量,Nst−st是测试集中恒星分为恒星的数量,Ngalaxy和Nstar分别表示测试集中星系和恒星的总数,测试集实验结果如表1所示.最后在实验1中SDA使用的具体参数范围为:网络结构是13-100-100-2,预训练学习率是0.1、0.01、0.005、0.001,预训练迭代次数是10、20、50、100,加噪噪声为掩蔽噪声,噪声系数为0.1、0.25、0.5,输出函数为Softmax函数,微调dropout系数为0、0.1、0.25、0.5,微调学习率为0.5、0.1、0.05、0.01,微调迭代次数为50、100、500、2000、5000.

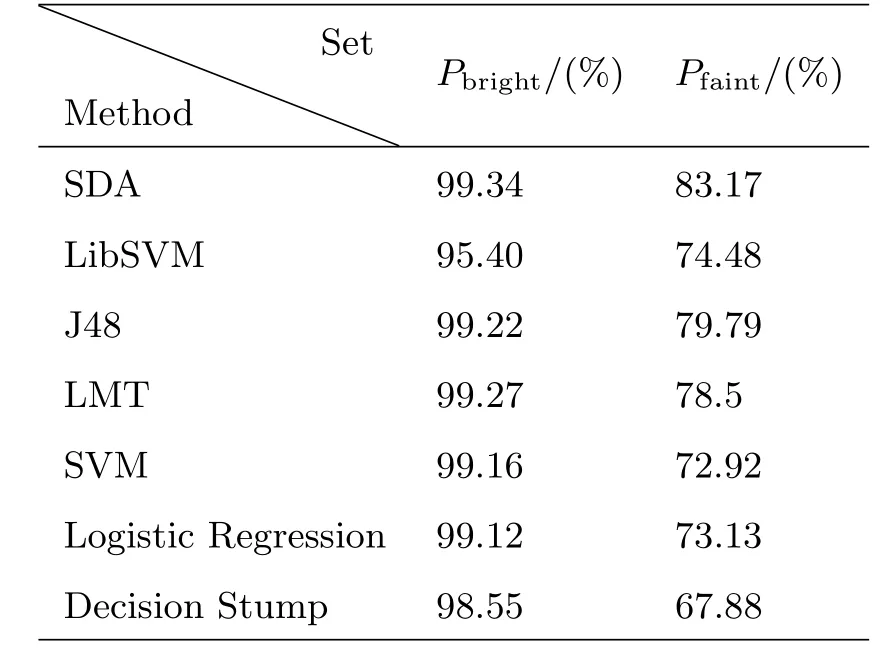
表1SDSS-DR12恒星/星系分类正确率Table 1 The accuracy rate of SDSS-DR12 star/galaxy classi fication

实验1结果说明在两个测试集中SDA的正确率都优于其余的机器学习算法,在亮源集部分由于整体的正确率都比较高,所以只是略优于其他算法,在暗源集部分SDA明显优于其他机器学习算法.Vasconcellos等人用决策树对SDSS-DR7数据进行了恒星/星系分类实验,实验结果显示在亮源集都取得了很高的正确率,但是在暗源集(modelMag值取20.5–21.0)正确率普遍偏低.作为比较实验2,我们将SDA在SDSSDR7亮源集(modleMag取值范围14.0–19.0)与暗源集(modleMag取值范围20.5–21.0,等值范围不同于SDSS-DR12)分类效果与决策树的分类效果进行比较.首先去除掉所提取的SDSS-DR7数据中带缺值的数据,再从亮源中随机抽取10000条恒星和10000条星系作为亮源训练集,抽取10000条星系数据和10000条恒星数据作为亮源测试集.接下来从暗源中随机抽取1000条恒星和1000条星系数据作为暗源测试集,剩余的315条暗源星系和920条恒星数据作为暗源测试集(暗源部分总的数据只有3000多条)并做归一化预处理,此外SDA网络的具体参数范围与实验1保持一致.为了保持与Vasconcellos等人所使用的测试指标保持一致,实验2我们使用完备函数(completeness function,CP)作为测试指标:

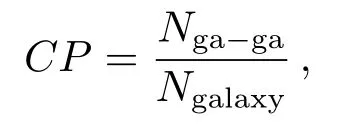
测试集分类正确率如表2所示.

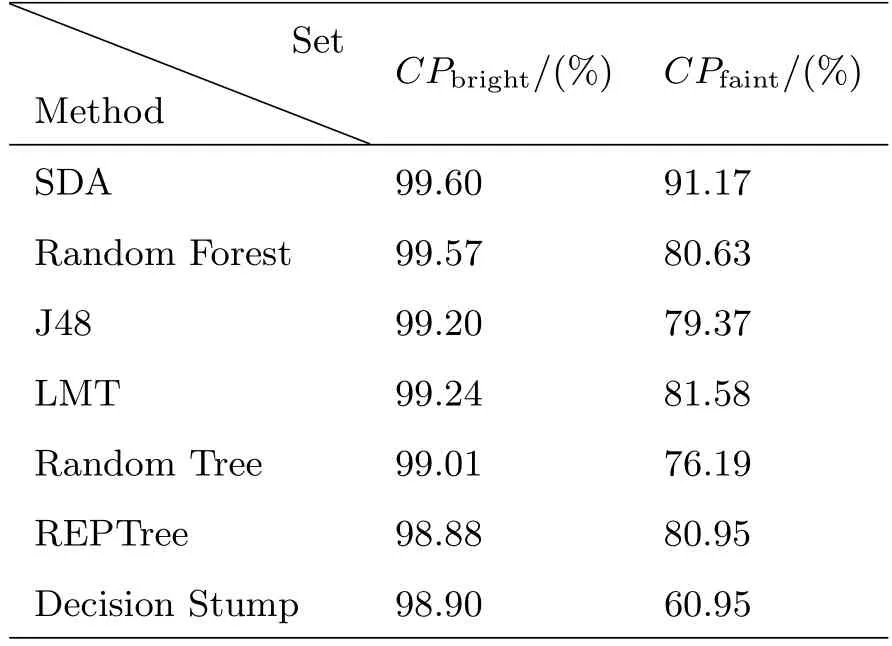
表2SDSS-DR7星系分类正确率Table 2 The accuracy rate of SDSS-DR7 galaxy classi fication

实验2结果说明在SDSS-DR7中SDA的恒星/星系分类性能优于决策树算法,其中亮源集部分正确率略优于决策树算法,而暗源集部分分类正确率远高于决策树算法,平均提高了15%左右.说明了SDA克服了决策树算法的不足,抓住了数据中隐藏的规律,不仅可以用于已出现过的数据,还可以用到未出现的数据中,具有很强的泛化能力.SDA性能优于传统算法的原因可能有以下几点:多层结构有更好的非线性函数逼近能力;利用非监督学习获得了更多的数据信息;逐层非监督初始化预处理为全局优化提供了较好的初始化参数;使用SDA消除了测量误差造成的数据噪声,并提取了更有效的特征.

5 总结与展望

本文通过使用SDA算法来研究SDSS恒星/星系分类问题,实验结果表明不管在新版的SDSS-DR12或者在SDSS-DR7上,相比于其他算法SDA都取得了很好的效果.尽管SDA表现优于其他算法,但是在暗源集的正确率还有待于进一步的提高.解决这个问题的方法我们认为有两个:第一,提高观测技术获取更多准确有效的暗源数据,大部分算法在暗源集表现不好的原因之一是受限于暗源数据集小和信号信噪比低;第二,算法改进,改进SDA的激活函数可能会是一个有效的方法.最后,虽然用SDA提高了分类正确率,但当实际应用的时候还会遇到数据量过大且处理速度太慢,难以满足实时性的问题.解决这个问题的途径可以依靠分布式平台对算法进行并行化改造,现在已经出现了基于深度学习的分布式工具,例如基于spark分布式平台的深度学习训练库OpenDL.接下来需要做的研究是将基于天文数据的深度学习算法和分布式处理工具相结合,做到准确性和效率的双提高,相信它将会极大地推动天文信息学的发展.

[1]Messier C.Connoissance des Temps for 1784,1781:227-267

[2]Sebok W L.AJ,1979,84:1526

[3]Kron R G.ApJS,1980,43:305

[4]Yee H K C.PASP,1991,103:396

[5]Henrion M,Mortlock D J,Hand D J,et al.MNRAS,2011,412:2286

[6]Leauthaud A.ApJS,2007,172:219

[7]MacGillivray H T,Martin R,Pratt N,et al.MNRAS,1976,176:265

[8]Heydon-Dumbleton N H,Collins C A,MacGillivray H T.MNRAS,1989,238:379

[9]严太生,张彦霞,赵永恒,等.中国科学G辑,2009,39:1794

[10]Vasconcellos E C,De Carvalho R R,Gal R R.AJ,2010,141:189

[11]Malek K,Solarz A,Pollo A,et al.A&A,2013,557:906

[12]York D G.AJ,2000,120:1579

[13]Hinton G E,Osindero S,Yw T.Neural Computation,2006,18:1527

[14]Bengio Y,Lamblin P,Larochelle H,et al.NIPS,2006:153

[15]Vincent P,Larochelle H,Bengio Y,et al.ACM,2008:1096

[16]Dahl G E,Sainath T N,Hinton G E.ICASSP,2013:8609

附录

SELECT

p.objID,p.ra,p.dec,s.specObjID,

p.psfMag-r,p.modelMag-r,p.petroMag-r,

p. fiberMag-r,p.petroRad-r,p.petroR50-r,

p.petroR90-r,p.lnLStar-r,p.lnLExp-r,

p.lnLDeV-r,p.mE1-r,p.mE2-r,p.mRrCc-r,

p.type-r,p.type,s.Class

INTO MyDB.SDSS-DR12-TRAIN-R13-23

FROM PhotoObj AS p

JOIN SpecObj AS s ON s.bestobjid=p.objid

WHERE

p.modelMag-r BETWEEN 13.0 AND 23.0 AND

s.Class in(’GALAXY’,’STAR’)AND

p.psfMag-r!=-9999 AND

p.modelMag r!=-9999 AND

p.petroMag r!=-9999 AND

p. fiberMag r!=-9999 AND

p.petroRad r!=-9999 AND

p.petroR50r!=-9999 AND

p.petroR90r!=-9999 AND

p.lnLStar r!=-9999 AND

p.lnLExp r!=-9999 AND

p.lnLDeV r!=-9999 AND

p.mE1r!=-9999 AND

p.mE2-r!=-9999 AND

p.mRrCc-r!=-9999

Stacked Denoising Autoencoders Applied to Star/Galaxy Classi fication

QIN Hao-ran1LIN Ji-ming1WANG Jun-yi2
(1 Guangxi Experiment Center of Information Science,Guilin University of Electronic Technology, Guilin 541004)
(2 Guangxi Key Laboratory of Cryptography and Information Security,Guilin University of Electronic Technology,Guilin 541004)

In recent years,the deep learning has been becoming more and more popular because it is well-adapted,and has a high accuracy and complex structure,but it has not been used in astronomy.In order to resolve the question that the classi fication accuracy of star/galaxy is high on the bright set,but low on the faint set of the Sloan Digital Sky Survey(SDSS),we introduce the new deep learning SDA(stacked denoising autoencoders)and dropout technology,which can greatly improve robustness and antinoise performance.We randomly selected the bright source set and faint source set from DR12 and DR7 with spectroscopic measurements,and preprocessed them.Afterwards, we randomly selected the training set and testing set without replacement from the bright set and faint set.At last,we used the obtained training set to train the SDA model of SDSS-DR7 and SDSS-DR12.We compared the testing result with the results of Library for Support Vector Machines(LibSVM),J48,Logistic Model Trees(LMT), Support Vector Machine(SVM),Logistic Regression,and Decision Stump algorithm on the SDSS-DR12 testing set,and the results of six kinds of decision trees on the SDSSDR7 testing set.The simulation shows that SDA has a better classi fication accuracy than other machine learning algorithms.When we use completeness function as the test parameter,the test accuracy rate is improved by about 15%on the faint set of SDSS-DR7.

methods:data analysis,techniques:photometric,galaxies:fundamental parameters,stars:fundamental parameters,cosmology:observations

P152;

:A

10.15940/j.cnki.0001-5245.2016.03.010

2015-07-15收到原稿,2015-12-22收到修改稿

∗国家自然科学基金项目(61261017)、广西自然科学基金项目(2014GXNSFAA118387)、广西信息科学实验中心项目(KF1408)及桂林电子科技大学研究生教育创新计划项目(YJCXS201517)资助

†19888nba@163.com

‡linjm@guet.edu.cn