三臂机器人在轨动力学仿真

黄晋英　杜为民　李　辉　蒋志宏　杨　欢

1.北京理工大学，北京，1010081　　2.中北大学，太原，0300513.中国民用航空河南空管分局，郑州，451162

三臂机器人在轨动力学仿真

黄晋英1,2杜为民3李辉1蒋志宏1杨欢2

1.北京理工大学，北京，10100812.中北大学，太原，0300513.中国民用航空河南空管分局，郑州，451162

摘要：根据航天机器人太空作业的需要，设计了三臂机器人简化模型，应用D-H方法建立了坐标变换矩阵，推导了该机器人的运动学方程。基于ADAMS虚拟样机技术，分别在三种重力场环境下，对机器人的爬杆过程进行仿真，得到了机械手攀爬过程受力曲线，分析了影响机械手夹持力的主要因素，从而为这类机器人的设计提供参考。

关键词：机器人；在轨；仿真；夹持力

0引言

太空环境极其恶劣，用机器人代替宇航员出舱完成装配、维修和搬运等工作十分必要[1-2]。空间环境与地面环境最大的区别是微重力,在微重力环境下，机器人处于漂浮状态，因此地面看似简单的工作将变得难以实现，其动力学行为与地面有较大差别，其运动学控制较为困难。多臂机器人与双臂机器人相比，多余的手臂可作为工作中的基座，从而克服了上述难题。三臂机器人可在结构上克服腿、臂独立结构构型机器人本体机构质量大、结构复杂等缺点，适用于太空作业，正日益引起人们的关注[3-4]。然而，这类空间机器人的研究仍处于起步阶段，本研究的目的就是通过机器人的在轨仿真，分析机器人在轨运动中的动力学行为，为其设计和应用提供参考。

1三臂机器人的系统模型

空间三臂机器人的简化模型如图1所示，其本体结构为一等边三角形，拥有3条完全相同的手臂。每条手臂由一组(2只)机械手、小臂和大臂组成，其上的腰关节、大臂关节、肘关节和小臂关节形成4个转动自由度，机械手的2只手掌与其轨道形成2个移动自由度，3条手臂共计18个自由度。工作时，由3条手臂交替攀爬航天器上设置的扶手到达指定位置，然后其中一条手臂固定在扶手上，其余两条手臂完成指定工作。这种三臂机构可使机器人具有多种灵活的运动步态和操作方式以适应不同的工况，极大地满足了空间机器人太空中工作的要求[5-6]。

图1　三臂机器人简化几何模型

1.1机器人空间坐标系的建立

按照D-H方法建立机器人系统坐标系，如图2所示。其中，OBXBYBZB是航天器的坐标系，OiXiYiZi是机器人各关节构件的动坐标系，机器人相邻两坐标系之间的矩阵用i-1T(i=1，2,…,n)表示，其中，i是机器人关节序号，前置序号i-1表示目的坐标系的序号，i-1=0表示机身坐标系。对于本文所设计的机器人，n=18。

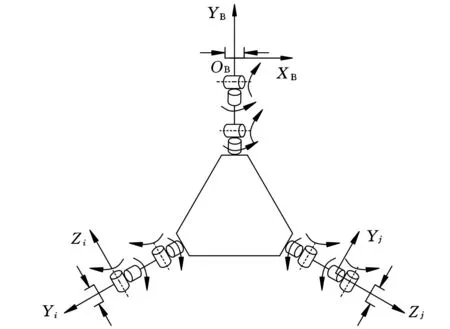
图2　三臂机器人空间坐标系

1.2机器人运动学方程的建立

机器人是由一系列具有空间弯曲轴线的广义连杆连接在一起构成的。根据三臂机器人的实际参数，可确定该模型的D-H参数，推导出三臂机器人的运动学方程方程[7-8]。记机器人的任意两个关节序号分别为i和i-1，如图3所示，固连在该2个关节上的动坐标系Z轴间的空间夹角(连杆扭角)为αi，空间最小距离(连杆长度)为bi，2个关节公垂线间的距离为di，2个关节X轴间的空间夹角(连杆夹角)为θi。

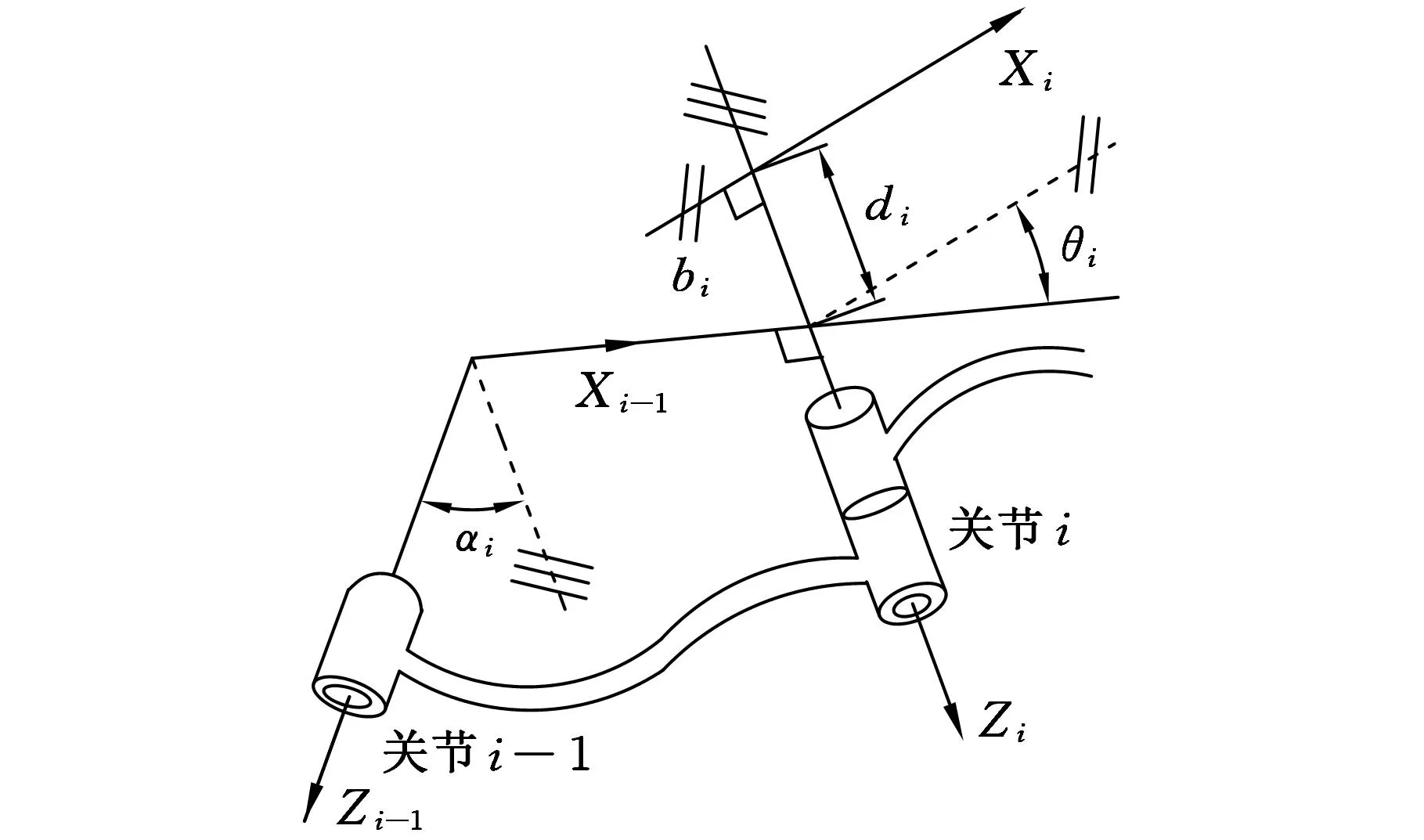
图3　广义连杆变换的4个特征参数D-H参数

上述D-H参数可通过如下两次旋转和两次平移坐标变换从坐标系OiXiYiZi变换到坐标系Oi-1Xi-1Yi-1Zi-1[8-10]：①将坐标系OiXiYiZi绕Xi-1旋转αi角，使Zi与Zi-1轴位于同一平面内；②将坐标系OiXiYiZi沿Xi-1轴平移bi，将坐标系OiXiYiZi原点移到Zi-1轴线上；③将坐标系OiXiYiZi绕Zi轴旋转θi角，使Xi轴与Xi-1轴平行；④将坐标系OiXiYiZi沿Zi-1轴平移di。

上述坐标变换可用如下坐标变换矩阵i-1Ti描述：

(1)

因此推导出三臂机器人每条臂的坐标变化矩阵为

T=TBT11T2…5T6

(2)

则机械臂末端在航天器坐标系下的位姿坐标可表示为

P=TPB

(3)

式中，PB为航天器的位姿坐标。

2三臂机器人的仿真模型

2.1机器人的简化几何模型

在Pro/E软件中建立三臂机器人的简化模型，直接将装配好的模型导入ADAMS软件中进行仿真，其简化模型如图1所示。该模型仅包含实现机器人运动所必需的机械构件，其余附件及电机等未涉及，简化模型的主要几何参数如图4所示。

图4　机器人简化模型的主要几何参数

2.2仿真模型建立

2.2.1模型质量设置

从Pro/E中导入的几何模型是没有质量的，在仿真前必须对各部件进行质量设置。本研究选用ADAMS软件材料库中的钛合金，并在重力(Gravity)选项中将重力设置为无重力(模拟微重力状态)或g/6(模拟月球环境重力)[11]，g为重力加速度。

2.2.2运动约束设置

在ADAMS/View环境中，模型构件之间的相互运动是靠运动副来实现的，在腰关节、大臂关节、腕关节和小臂关节之间添加旋转副，在机械手添加移动副，其余构件添加固定副约束。

2.2.3接触定义

当两个构件表面间发生接触并存在相对运动趋势时，这两个构件会在接触区产生摩擦力，摩擦力随接触面正压力的增大而增大，在ADAMS中称为接触力[12]。三臂机器人攀爬仿真过程中，当机械手抓住航天器上的杆状扶手时，需要定义机械手与扶手之间的接触。本研究选用IMPACT型接触力和库仑摩擦，其参数如表1所示。其中，材料刚度、阻尼和摩擦因数由材料性质所决定。

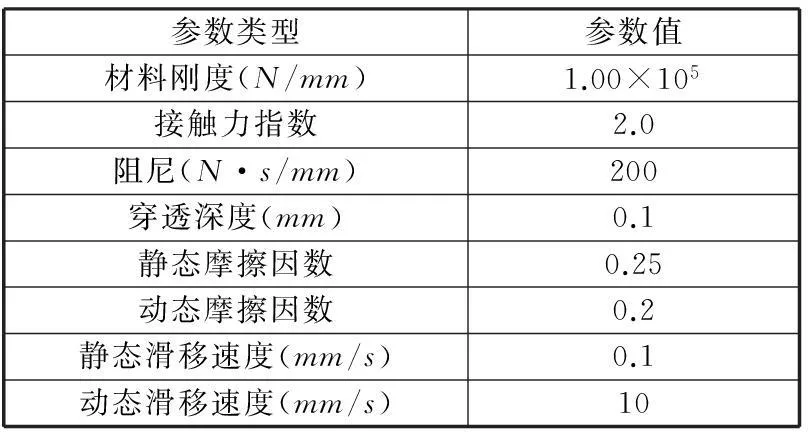
表1　仿真过程中接触参数设置

2.2.4运动轨迹设计与驱动添加

对机器人模型施加驱动就是让其未受约束的运动副按照某种规律变化。根据机器人的几何结构特点，在仿真过程中只需要添加旋转驱动与滑移驱动，将旋转驱动添加到旋转副和圆柱副，将滑移驱动添加到滑移副和圆柱副。每个运动副需要编写独立的驱动函数，以完成规定的运动轨迹。在本研究中，仿真运动轨迹规定为三臂轮流抓杆向前移动，起始动作为1号机械手抓杆，2号机械手开始运动抓杆；当2号机械手抓稳杆后，1号机械手脱离杆，同时3号机械手重复前述动作准备抓杆；如此往复，实现机器人沿攀爬杆向前运动。在整个攀爬过程中，机器人始终与YBOBZB平面平行，机械手的夹持力方向平行于XB轴。

本文仿真中实现上述运动的驱动函数采用step函数编写。step函数是ADAMS函数库中常用的函数，是三次多项式逼近阶跃函数，由5个参数控制，分别为自变量(x)、自变量的初值(x0)和终值(x1)，函数值的初值(h0)和终值(h1)。在仿真中，从初值到终值的过程由软件按照三次样条拟合自动计算给出。step函数的具体格式为

step(x,x0,h0,x1,h1)

图5为由step函数拟合得到的运动轨迹曲线[13]。本研究中采用时间位移驱动，即要求各关节在规定的时间内运动到规定的位置，自变量为时间坐标。图6为爬杆过程步态图。

图5　step函数拟合轨迹曲线

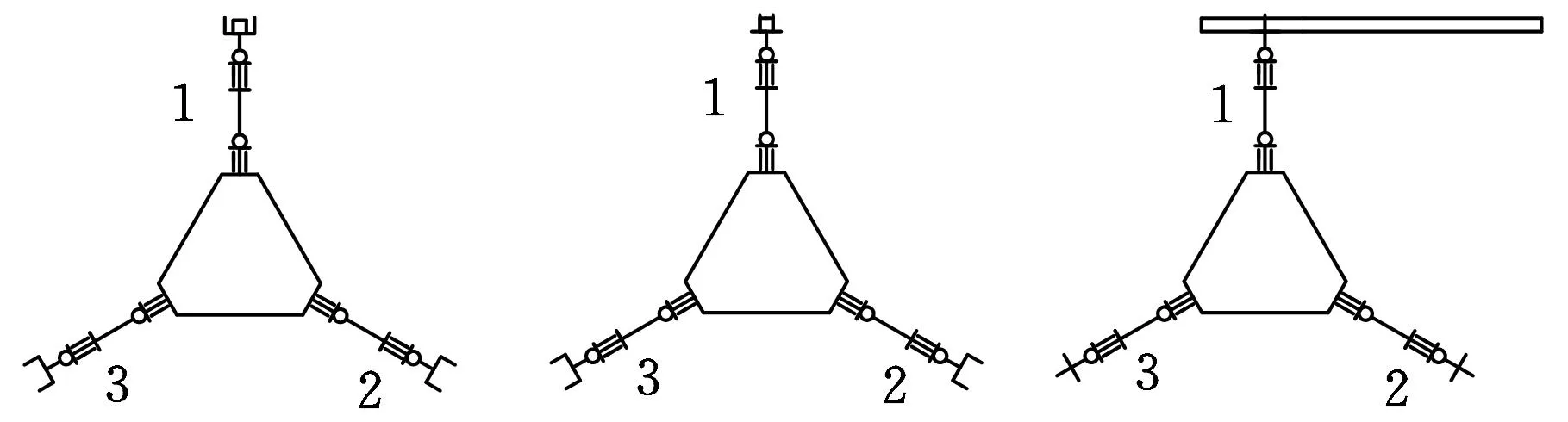
(a) (b)(c)

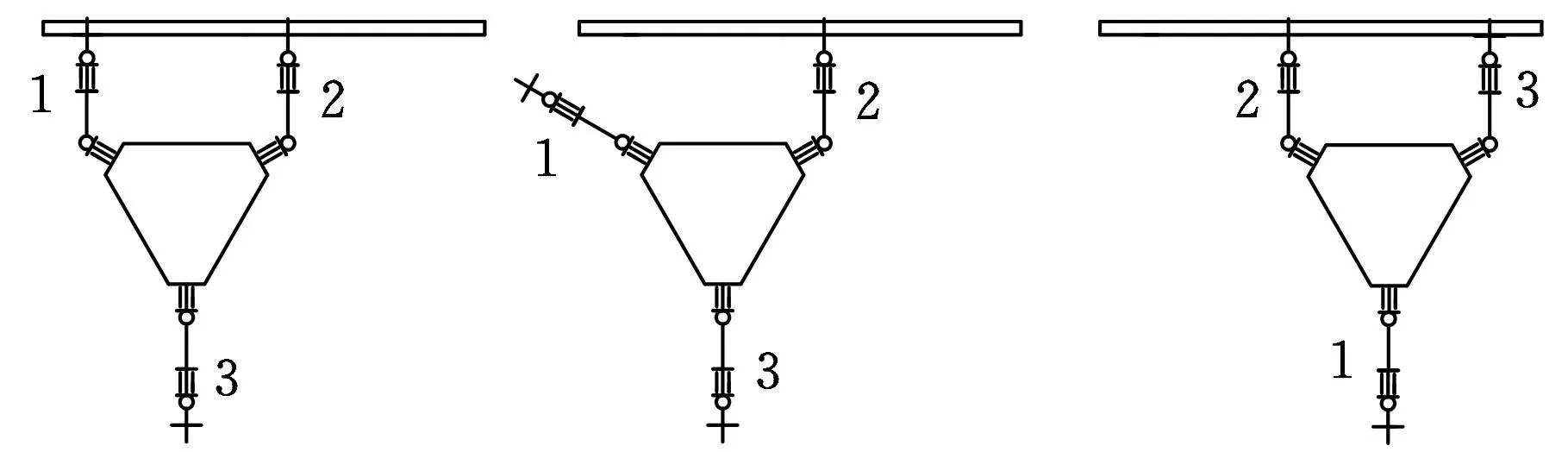
(d) (e)(f)图6　机器人仿真步态示意图

基于上述驱动函数，设计运动过程如下：

(1)初始位置设为1号手臂抓杆前的位置，3条手臂伸直与机身位于同一平面内，即XBOBYB平面，1号手臂平行于YB轴，其余两条手臂与之成120°，杆置于1号机械手内，见图6a。

(2)1号手臂的两只机械手沿杆轴线方向运动(XB向)闭合抓杆，见图6b，运动时间0.1s。

(3)除1号手臂外，其余部件绕1号手臂腰关节旋转90°，机器人在YBOBZB平面内运动，运动时间1 s，见图6c。

(4)2、3号手臂和机身绕1号手臂大臂关节在YBOBZB平面内旋转60°，然后，2号手臂绕其大臂关节再旋转60°，2号手臂到达抓杆前状态，运动时间共计4s，见图6d。

(5)2号手臂的两只机械手闭合抓杆，其运动时间为1s；1、2号手臂同时抓杆时间持续1s。

(6)1号手臂的两只机械手向杆的反方向运动，松开爬杆，运动时间1s。

(7)1号手臂绕其大臂关节旋转-60°，1、3号手臂和机身绕2号大臂关节在YBOBZB平面内旋转-120°，3号手臂绕其大臂旋转60°，3号机械手到达抓杆前位置，见图6e和图6f。

(8)3号手臂的两只机械手闭合抓杆，其运动时间和驱动函数同过程(2)中设置，两只手同时抓杆时间持续1s。

(9)重复上述过程，实现机器人的整个攀爬过程。

不失一般性，本文仅对1号手臂抓两次杆，2、3号手臂各抓一次杆进行仿真。1号机械手驱动函数为

step(time,0,0,0.1,-17.2)+step(time,9,0,10,17.2)+

step(time,31,0,33,-17.2)

其余驱动函数在此不再列出。为减小同时动作带来的振动影响和前一次动作对后一次动作的影响，在编制驱动函数时，所有运动副的动作时间不重叠。

3仿真结果及分析

本文在无重力和不同方向g/6重力环境下分别对三臂机器人的爬杆过程进行动力学仿真，获得不同环境下机械手受力情况和大臂关节运动过程扭矩曲线，为机器人的设计提供参考。

3.1机械手受力情况分析

图7～图9分别为三臂机器人在无重力、g/6重力环境下3条手臂的机械手受力曲线，其中，CONTACT_1.FX为1号手臂的机械手夹持力(XB向)曲线，CONTACT_5.FX为2号手臂的机械手夹持力(XB向)曲线，CONTACT_8.FX为3号手臂的机械手夹持力(XB向)曲线。重心位于机器人几何中心。

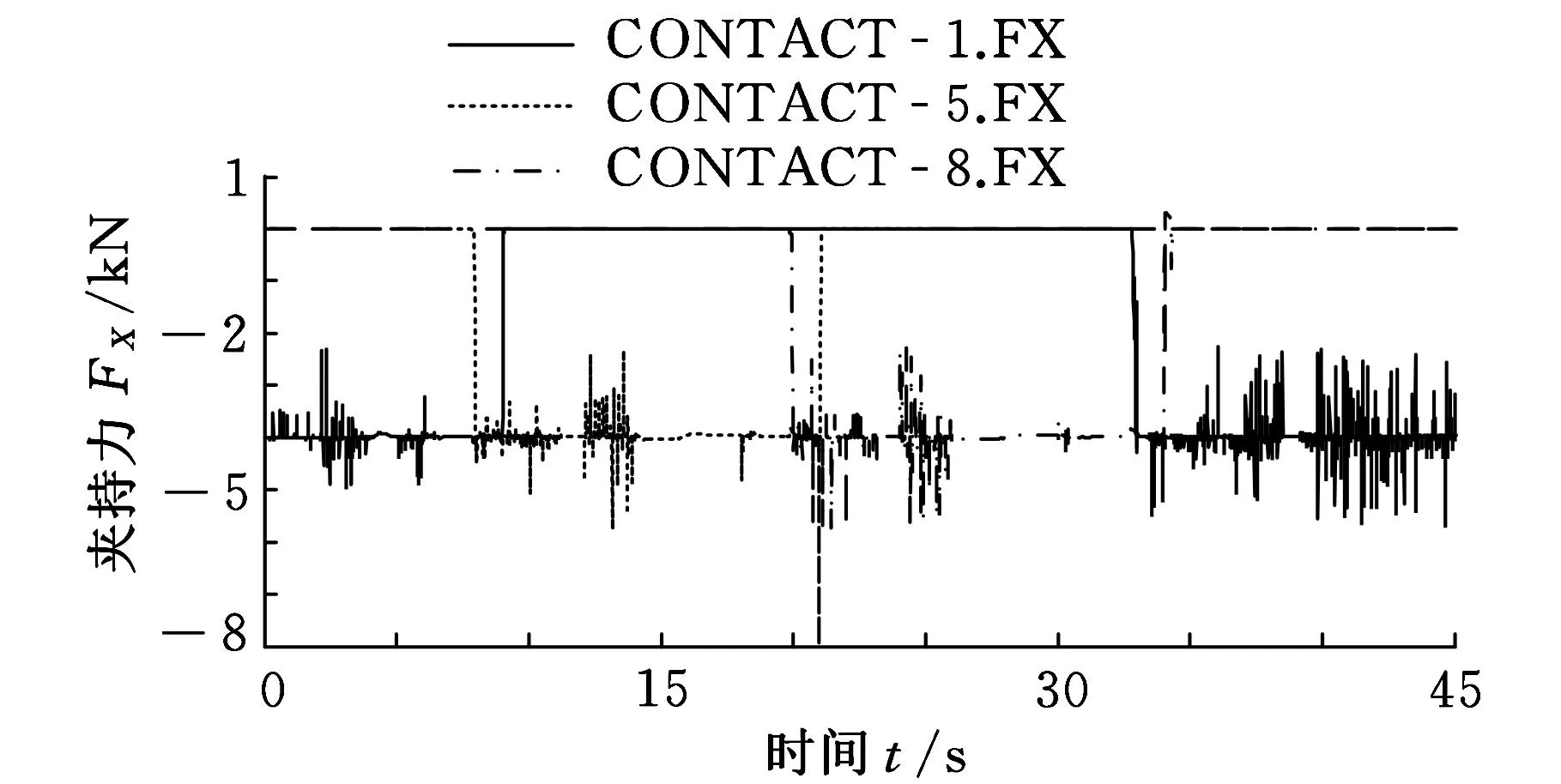
图7　无重力环境下3条手臂机械手受力情况

图8　重力平行于XB轴环境下3条手臂机械手受力情况

图9　重力平行于-YB轴环境下3条手臂机械手受力情况

由上述仿真结果可见，虽然1号手臂首次抓杆持续时间远远短于其他两条手臂和1号手臂第二次抓杆持续时间，但3条手臂的机械手在抓杆过程中受力基本一致。由此可知，抓杆过程的速度变化基本不影响夹持力的大小。在整个爬杆过程中，机体运动会引起机械手与杆之间的相对运动，如图10所示。图10a所示为理论抓杆状态，机械手两侧手掌和轨道与杆的3个平面完全接触，在所允许的切入深度下紧握爬杆，但实际中会出现图10b～图10d所示的情况。图10b两侧手掌切入深度不一致(左侧大于右侧)，图10c和图10d接触面变为部分接触，这种接触方式之间的变换导致接触力发生波动。

(a)(b)

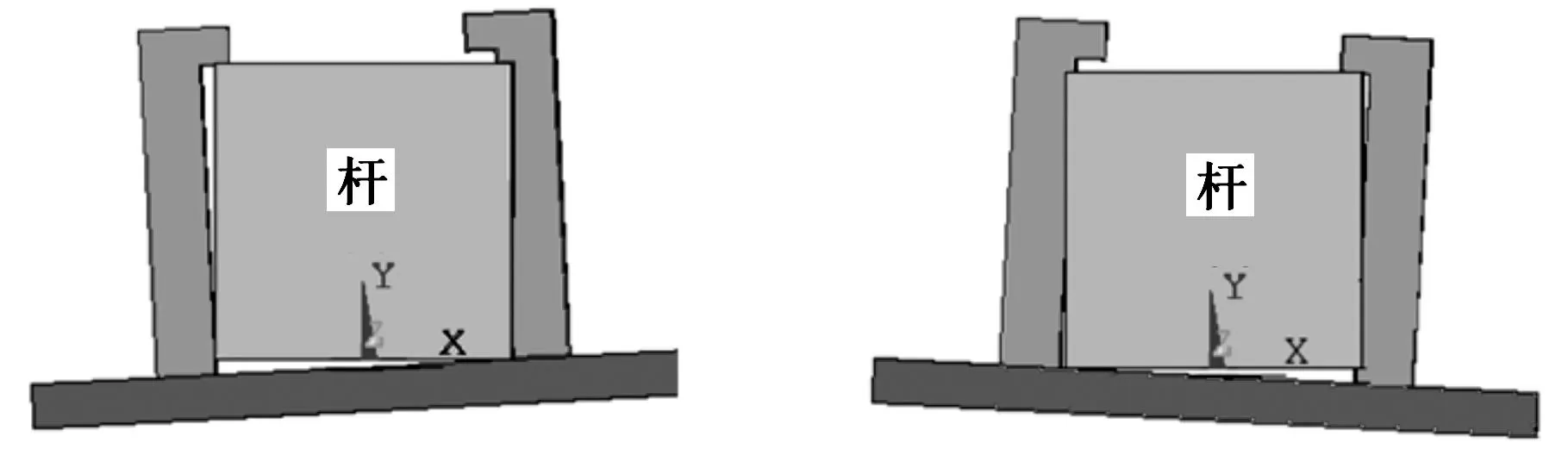
(c)(d)图10　机械手抓杆接触状态

例如，2～3s时，1号机械手抓紧爬杆，机身绕YB轴旋转，转动过程对机械手的受力影响较大，造成夹持力发生波动，如图11所示。一侧手掌夹持力增大的同时另一侧手掌夹持力减小，为防止机械手脱离爬杆，控制两侧手掌的接触力在某一数值(如-4000N)上下波动。图11中2条曲线分别为1号机械手在无重力情况下两只手掌的夹持力曲线，夹持力峰值最大达到-5700N，波动幅度与平均夹持力相比增大30%。11～17s时1号手臂脱离爬杆,3号手臂向抓杆位置摆动，夹持力峰值在12～14s期间波动较大,达到-5785N，如图12所示。机体转动惯性会使机体发生晃动，严重的晃动不仅造成夹持力波动，若控制不当甚至会使机械手滑落爬杆，因此，应进一步考察机身转动速度对夹持力的影响情况。

图11　无重力情况下1号机械手夹持力

图12　无重力情况下2号机械手夹持力

图13所示为三种重力情况下2号机械手夹持力曲线对比，图中曲线1为无重力情况下仿真结果，曲线2和3分别为重力方向为XB向和-YB向的仿真结果。值得指出的是，重力对夹持力有较大影响。当重力方向与夹持力方向一致(即重力方向为XB向)时，重力在造成夹持力增大的同时，还会使得两只机械手夹持力不相等，在快速抓杆时出现多次碰撞(图10)，导致抓杆困难。当重力方向与夹持力方向垂直(即重力方向为-YB向)时，重力使得夹持力波动幅度和频率减小。以上情况表明，无重力状态的运动姿态较重力场中的运动姿态更难控制。

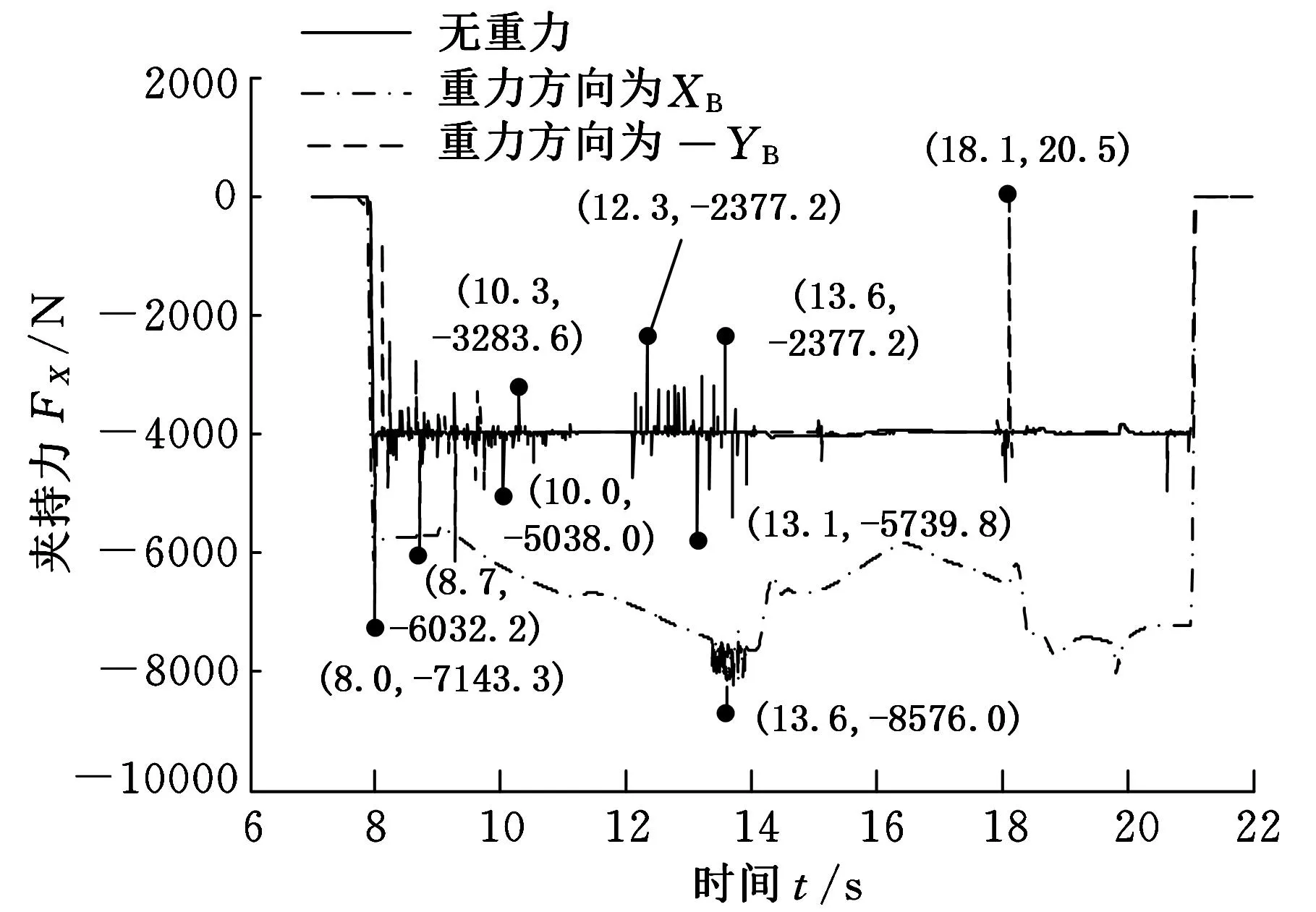
图13　三种重力情况下2号机械手夹持力

3.2机械手轨道受力情况分析

对于上述设计步态，在机械手与爬杆接触之前，机械手轨道的一端首先与杆发生碰撞，此后逐渐碰撞到达指定部位(图14中从右至左)。此时轨道平面与杆平面接触或平行，该过程会给大臂关节形成冲击，造成大臂关节逆向转动。如果驱动力矩不够大，则机械手将无法到达抓杆前指定位置。图15～图17为三种环境下轨道的受力情况，其中CONTACT_6.FY为1号机械手轨道的受力曲线，CONTACT_3.FY为2号机械手轨道的受力曲线(-YB向)，CONTACT_9.FY为3号机械手轨道的受力曲线，2号机械手轨道方向与其他二只机械手轨道的坐标方向相反。

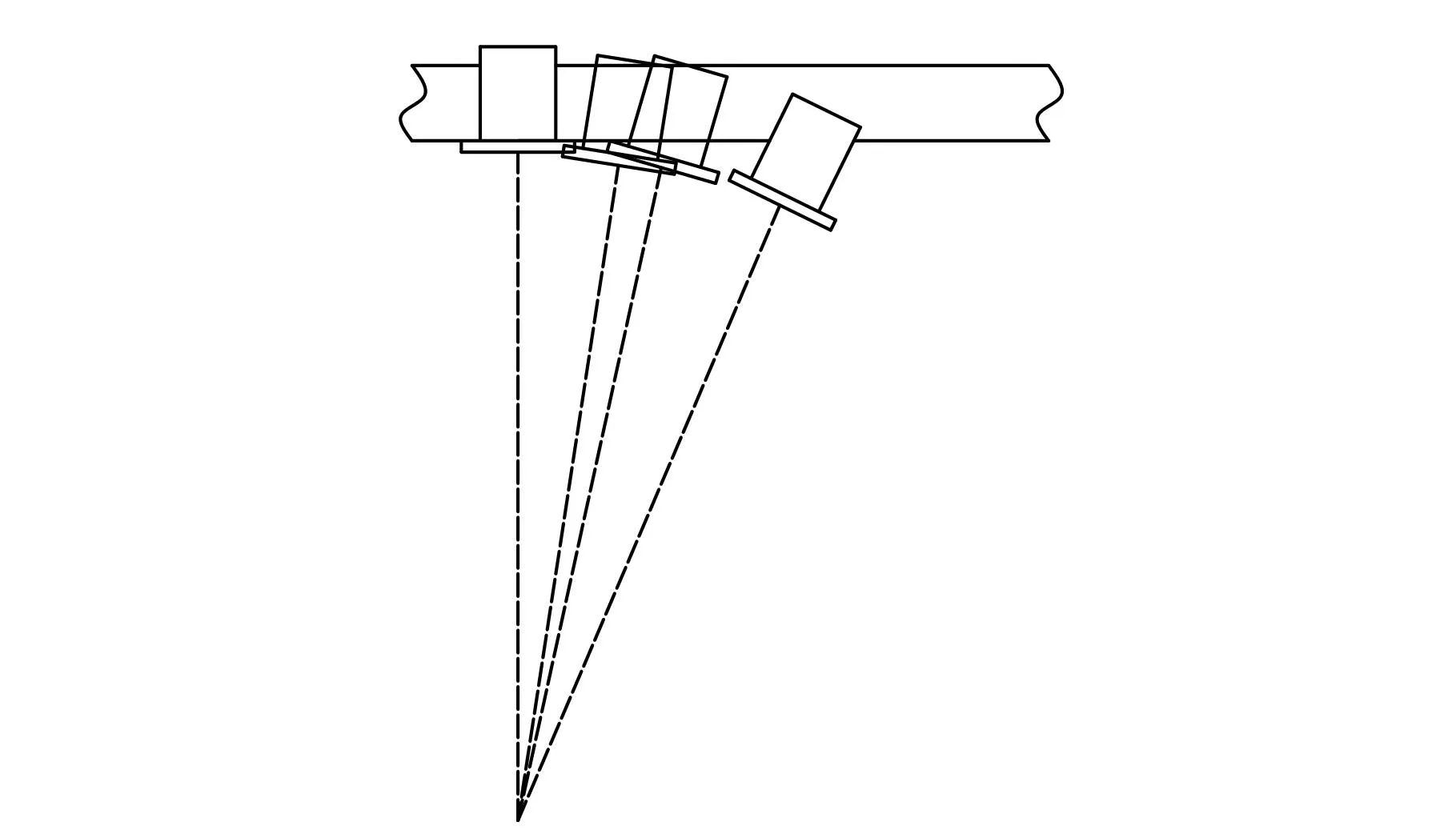
图14　机械手轨道与杆碰撞过程

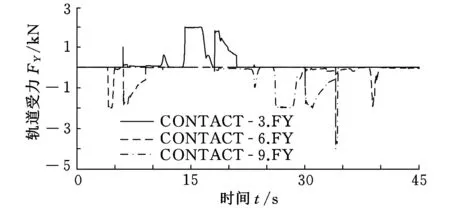
图15　无重力环境下3条手臂机械手轨道受力情况

图16　重力平行于XB轴环境下3条手臂机械手轨道受力情况

图17　重力平行于-YB轴环境下3条手臂机械手轨道受力情况

由上述曲线看出，在机械手抓紧爬杆后手掌和杆接触面之间的相对运动比较频繁，导致轨道接触力频繁波动。从碰撞力来看，重力平行于XB轴环境下碰撞力最大。表2为各种环境下机械手及其轨道最大受力汇总表。

表2　三种环境下机械手受力　N

4结论

(1)对于本文设计的步态，为了验证抓杆速度和多关节同步运动对机械手夹持力的影响，对1号机械手和2、3号机械手分别采用不同抓杆速度进行仿真分析，结果表明，抓杆速度对夹持力的影响不明显。在腰部回转时采用多关节联动、其他关节单独运动的方式进行仿真分析，结果表明，多关节联动会造成机器人振动加剧，夹持力增大，夹持力波动加大，故在设计机器人控制策略时应尽量避免多关节联动。

(2)重力对机器人的姿态影响较大，在设计重力环境下机器人攀爬路线时，应尽量让重力和夹持力与杆长度方向垂直(重力为-YB向)，这样可使姿态容易保持稳定。

(3)应改进设计机械手轨道，尽量减少其边缘对杆的碰撞；同时改变关节运动顺序，将边缘首先碰撞改为整个轨道平面与杆全接触，这样可减小碰撞力引起的机器人振动。

(4)在仿真过程中，仿真参数设置对仿真结果影响较大，本文所设置的参数主要以经验值为依据，仿真结果可为这类空间机器人的设计与控制提供定性参考。

参考文献：

[1]RastegariR,MoosavianSAA.MultipleImpedanceControlofSpaceFree-flyingRobotsviaVirtualLinkages[J].ActaAstronautica, 2010, 66:748-759.

[2]梁捷, 陈力. 双臂空间机器人基于高斯型函数的姿态、关节运动模糊自适应补偿控制[J]. 中国机械工程, 2010, 21(3):330-336.

LiangJie,ChenLi.FuzzyAdaptiveCompensationControlforSpace-basedRobotSystemwithDual-armBasedonGaussian-typeFunctiontoTrackTrajectoryinJointSpace[J].ChinaMechanicalEngineering, 2010, 21(3):330-336.

[3]慧记庄, 魏芳胜, 高凯，等. 基于ADAMS的冗余驱动并联机器人动力学仿真研究[J]. 工程设计学报, 2012,19(5): 362-365.

HuiJizhuang,WeiFangsheng,GaoKai,etal.StudyonDynamicsSimulationofRedundantlyActuatedParallelRobotBasedonADAMS[J].ChineseJournalofEngineeringDesign, 2012,19(5): 362-365.

[4]孙汉旭, 贾庆轩, 张秋豪, 等. 基于三分支机器人关节空间轨迹规划的研究[J]. 北京邮电大学学报, 2006, 29(3):81-85.

SunHanxu,JiaQingxuan,ZhangQiuhao,etal.TrajectoryPlanninginJointSpaceBasedonTri-BranchRobot[J].JournalofBeijingUniversityofPostsandTelecommunications, 2006, 29(3):81-85.

[5]孙汉旭，姬罗栓，徐扬生. 空间三臂机器人在操作中的平衡问题[J]. 北京邮电大学学报, 2002,25(1):34-38.

SunHanxu,JiLuoshuang,XuYangsheng.StudyofBalanceProblemforaThree-armSpaceRobotduringItsManipulation[J].JournalofBeijingUniversityofPostsandTelecommunications, 2002, 25(1):34-38.

[6]叶平, 孙汉旭. 具有冗余度的三分支空间机器人逆运动学分析[J]. 机械工程学报, 2005, 41(11):58-62.

YePing,SunHanxu.AnalysisofInverseKinematicsforThree-branchSpaceRobotwithRedundancy[J].ChineseJournalofMechanicalEngineering, 2005, 41(11):58-62.

[7]SugaTG,KumarV.ControlofCooperatingMobileManipulators[J].IEEETransactiononRoboticsandAutomation, 2002, 18(1)：94-103.

[8]方琛玮. 基于ADAMS机器人动力学仿真研究[D]. 北京：北京邮电大学，2009.

[9]ZhuangYF,LiuDQ,WangJG.DynamicModelingandAnalyzingofaWalkingRobot[J].TheJournalofChinaUniversitiesofPostsandTelecommunications, 2014, 21(1):122-128.

[10]甘屹, 王均垒, 孙福佳. 基于给定工作空间的6R型机器人D-H参数优化设计[J]. 中国机械工程, 2014, 25(22):3003-3007,3011.

GangYi,WangJunlei,SunFujia.OptimalDesignofD-HParametersofa6RRobotforaPrescribedWorkspace[J].ChinaMechanicalEngineering, 2014, 25(22):3003-3007,3011.

[11]姬广勋. 履带式载人月球车移动系统的设计与运动性能分析[D]. 哈尔滨：哈尔滨工业大学, 2013.

[12]SharfI,ZhangYN.AContactForceSolutionforNon-collidingContactDynamicsSimulation[J].MultibodySystemDynamics, 2006, 16(3):263-290.

[13]阮鹏, 俞志伟, 张昊, 等.基于ADAMS的仿壁虎机器人步态规划及仿真[J]. 机器人，2010, 32(4):499-509.

RuanPeng,YuZhiwei,ZhangHao,etal.GaitPlanningandSimulationofGeckoInspiredRobotBasedonADAMS[J].Robot, 2010, 32(4):499-509.

(编辑苏卫国)

Dynamic Simulation for a Three-arm Robot on Orbit

Huang Jinying1,2Du Weimin3Li Hui1Jiang Zhihong1Yang Huan2

1.Beijing Institute of Tecnology,Beijing,100081 2.North University of China,Taiyuan,030051 3.Henan Branch of Air Traffic Control of Civil Aviation of China,Zhengzhou,451162

Abstract:A simplified robot model with three arms was designed according to the needs of space operations. The coordinate transformation matrix was established based on the D-H method and the kinematic equations of the robot were derived. Based on ADAMS virtual prototyping technology, the climbing process of the robot on a pole was simulated for three kinds of gravity, respectively. The force curves and effect factors were obtained so as to offer the design references for the robot.

Key words:robot; on orbit; simulation; clamping force

收稿日期：2014-08-15修回日期：2015-12-07

中图分类号：TP241.2

DOI：10.3969/j.issn.1004-132X.2016.03.008

作者简介：黄晋英, 女, 1971年生。北京理工大学宇航学院博士后研究人员，中北大学机械与动力工程学院教授。主要研究方向为动力学分析与控制。杜为民，女，1966年生。中国民用航空河南空管分局高级工程师。李辉，男，1982年生。北京理工大学机电学院讲师。蒋志宏，男，1974年生。北京理工大学机电学院副教授。杨欢，男，1988年生。中北大学机械与动力工程学院硕士研究生。