RV减速器扭转振动的固有特性及灵敏度分析

刘柏希　王文军　聂松辉

湘潭大学，湘潭，411105

RV减速器扭转振动的固有特性及灵敏度分析

刘柏希王文军聂松辉

湘潭大学，湘潭，411105

摘要：以RV减速器为研究对象，综合考虑系统刚度和摆线轮偏心角度对扭转振动特性的影响，采用集中参数法，建立了该系统13个自由度的修正扭转动力学模型。通过求解自由振动方程得到系统固有频率及主振型，分析了摆线轮偏心角度对系统固有频率的影响。利用偏导数法分析了系统固有频率对转动惯量和刚度的影响。研究结果表明，轴承刚度为系统固有频率的关键影响因素。

关键词：RV减速器；扭转振动；固有特性；灵敏度分析

0引言

RV减速器是由K-H型行星传动与K-H-V型行星传动复合而成的一种新型传动机构，具有体积小、刚度高、传动比大等一系列优点，被广泛运用于工业机器人、雷达等领域[1]。由于机器人等机构对低振动水平的要求特别严格，因此有必要对RV减速器的动态特性进行研究，以解决机器人的抖颤问题。

国内外学者对RV减速器传动精度的研究较为深入，取得了丰富的研究成果。但涉及RV减速器动力学特性的研究还不多。Mirko[2]建立了摆线行星传动的动力学仿真模型，分析了系统各构件位移及速度的动态响应；张大卫等[3]建立了摆线针轮传动副的啮合刚度模型，分析了结构参数对啮合力的影响；王刚等[4]计算了摆线针轮啮合刚度并建立了五自由度的扭转模型；严细海等[5]基于等效原理建立了五自由度的等效扭转模型；Hsieh[6]考虑摆线传动的接触条件，建立了动力学模型，研究了系统的运动和应力特性；李充宁等[7]利用ADAMS对2K-V减速器进行了多刚体动力学仿真，得到了摆线轮的固有频率及动态啮合力。经过国内外学者的努力，较为精细的RV减速器动力学模型已建立，但上述模型均未考虑摆线轮偏心角度的变化对系统动力学的影响，也未定量研究系统转动惯量和刚度对固有频率的影响。

笔者根据RV减速器的传动原理，考虑曲柄轴和摆线轮公转运动的切向平移自由度以及摆线轮偏心角度的变化，建立修正扭转动力学模型，计算系统的固有频率及主振型，并利用偏导数法对系统固有频率灵敏度进行分析，分析固有频率对系统转动惯量和刚度的灵敏度。

1RV传动原理

1.太阳轮　2.行星轮　3.曲柄轴　4.摆线轮5.针齿　6.行星架　7.针齿壳图1　RV传动的机构简图

RV传动的机构是由渐开线与摆线齿轮组成的二级行星轮系，如图1所示。高速级为渐开线齿轮组成的K-H 型差动轮系，由太阳轮、径向均匀分布的n(n=2，3)个行星轮和行星架组成；低速级为摆线齿轮组成的K-H-V 型行星轮系，由径向均匀分布的曲柄轴、2个对称布置的摆线轮、若干针齿以及行星架组成。曲柄轴的偏置方向一致，一端与对应的行星轮固连，另一端与行星架上对应的销孔组成转动副，轴中部则与摆线轮构成转动副。

RV传动的传动原理为：电机的顺时针转动由太阳轮传递给n个行星轮，实现第一级减速；行星轮的转动作为第二级减速部分的输入传递给与其连成一体的曲柄轴，曲柄轴逆时针方向的自转带动摆线轮产生偏心运动(公转运动)。针轮固定后，摆线轮在公转的同时，还将反向自转(顺时针转动)。摆线轮的自转带动曲柄轴做公转运动，曲柄轴将此运动通过行星架上的轴承传递给行星架，使其做顺时针转动，即以1∶1的速比将摆线轮的自转转化为输出转速。

2系统修正扭转动力学模型的建立

RV传动包含曲柄轴和摆线轮的公转运动，其输出转动是通过曲柄轴的公转运动实现的，故现有的RV减速器纯扭转动力学模型仅考虑曲柄轴和摆线轮的扭转自由度是不够精细的，应进一步计入曲柄轴和摆线轮的公转运动的平移自由度。偏心曲柄轴带动摆线轮做偏心运动过程中，曲柄轴与摆线轮的相互作用力会随摆线轮质心的偏心角度的周期性变化而变化[8]，但现有的动力学模型并没有考虑此种变化对系统动态特性的影响。

基于以上分析，本文采用集中参数法，考虑曲柄轴和摆线轮公转运动的切向平移自由度，以及曲柄轴与摆线轮作用力周期性变化等因素，建立系统的修正扭转动力学模型。

动力学模型基于以下简化和假设：①采用集中参数模型，并认为各构件的几何中心与其质心重合；②轴承刚度和齿轮啮合刚度取其均值，忽略其刚度非线性变化；③忽略啮合副的摩擦力和阻尼的影响；④摆线轮与针轮间的啮合力按集中力处理；⑤曲柄轴上轴承之间间距很小，使得曲柄轴弯曲刚度较大，经计算可知其弯曲刚度至少为轴承刚度的5倍，故可忽略曲柄轴的弯曲变形；⑥公转运动过程中，行星轮和曲柄轴的切向平移自由度相同。

如图2所示，以针轮中心O为原点，建立与行星架固连的动坐标系Oxy，y轴指向第一个曲柄轴理论轴线与摆线轮的交点Oh1，动坐标系Oxy随行星架以理论角速度ωc匀速转动；设定第一个摆线轮的理论中心Oc1与针轮中心O连线OOc1初始时与y轴一致，随着摆线轮的公转，OOc1与y轴的夹角变为β。在第一个摆线轮上建立与其固连的动坐标系Oηζ，使ζ轴指向摆线轮偏心方向OOc1。

图2　RV减速器动力学模型

为简化图形，图2中只表示了第一个曲柄轴，同理可建立相对于第二个曲柄轴的坐标系。据此可得动力学模型的13个自由度：输入轴、太阳轮、2个行星轮、2个曲柄轴、2个摆线轮与行星架的9个扭转自由度，2个曲柄轴与2个摆线轮公转运动的4个切向平移自由度。两曲柄轴编号为i(i=1，2)，两摆线轮编号为j(j=1，2)。图2中，ua、us、upi、uhi、ucj、uo分别为输入轴、太阳轮、行星轮、曲柄轴、摆线轮和行星架振动扭转角位移折算到圆周上的线位移。xhi、xcj分别为曲柄轴和摆线轮的公转运动平移线位移。各位移方向的规定如下：输入轴顺时针转动时，以各个构件实际运动方向为位移正方向，不同构件间作用线上的相对位移方向由接触面的受力来规定，当接触面所受的力为压力时，规定该相对位移方向为正方向。系统受力最为复杂的是曲柄轴与摆线轮间的作用力，现以其为例进行受力分析，如图3所示。

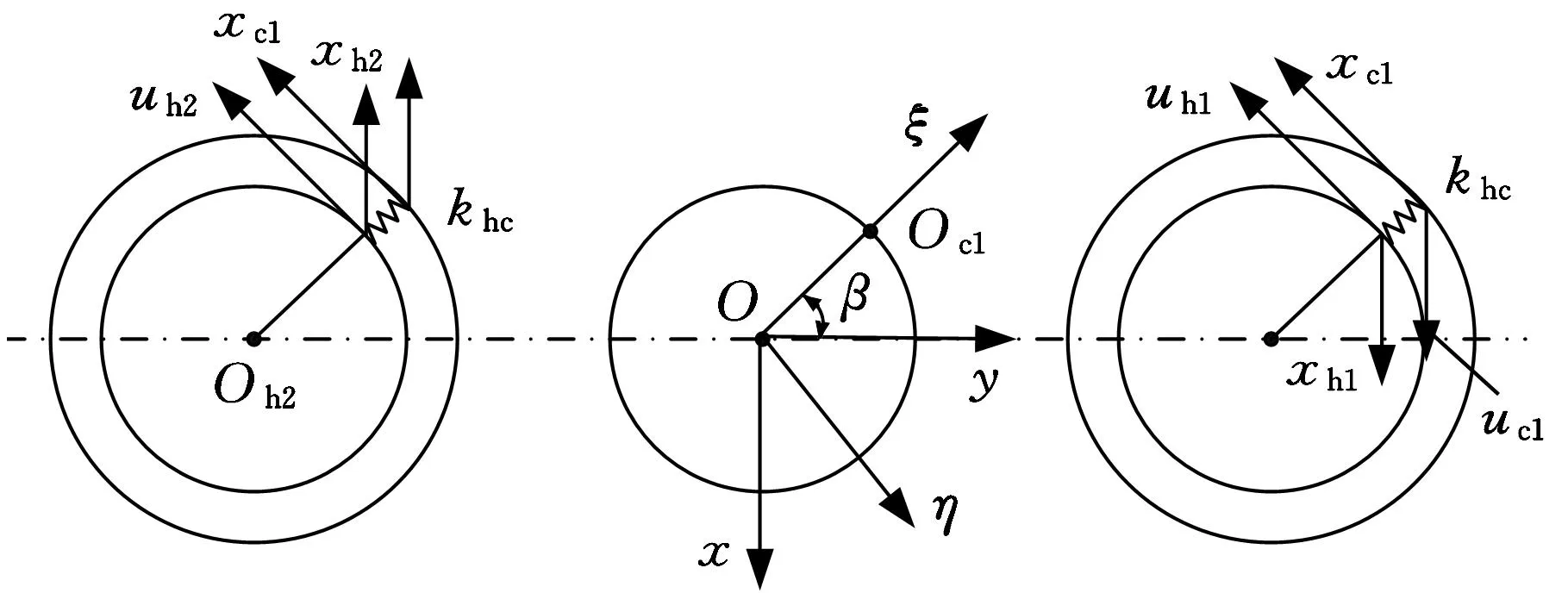
图3　第一个摆线轮与曲柄轴动力学模型局部图

由图3可知，曲柄轴和摆线轮的相对位移在η向的投影为

(1)

βi=β+(i-1)π

(2)

则曲柄轴和摆线轮之间在η向的作用力为

Fhicj=khcδη ij

(3)

其中，khc为转臂轴承的支承刚度。同理可推导出两者之间在x方向的作用力：

(4)

限于篇幅，其他构件间作用力不一一列举，根据牛顿第二定律可得系统自由振动方程：

(5)

Fspi=ksp(us-upi-xhicosα)

(6)

式中，Ja、Js、Jp、Jh、Jc、Jo分别为输入轴、太阳轮、行星轮、曲柄轴、摆线轮和行星架的转动惯量；mp、mh、mc分别为行星轮、曲柄轴和摆线轮的质量；α为渐开线齿轮啮合压力角；a为偏心距；rs、rp分别为太阳轮和行星轮的基圆半径；rh为曲柄轴分布圆半径；rc为摆线轮节圆半径；kas、kph分别为输入轴和曲柄轴扭转刚度；ksp、kcd分别为渐开线齿轮和摆线针轮啮合刚度；khc、koh分别为转臂轴承和支撑轴承的支承刚度；Ts、Tc分别为输入转矩和输出转矩。

整理式(5)可得矩阵形式的动力学一般方程：

(7)

式中，X、M、K、F分别为广义坐标列阵、质量矩阵、刚度矩阵和广义力列阵。

本文研究的是系统固有特性，则令输入转矩的值为0，即广义力列阵F为0列阵。

3系统固有特性分析

模态(特征值与特征矢量)是决定模型实际响应的内在依据，利用模态理论对上述动力学模型进行分析，可得式(7)对应的特征方程：

(8)

式中，ωi为系统第i阶固有频率；φi为ωi对应的正则化振型。

求解式(8)可获得系统的各阶固有频率和振型。

以RV-6型减速器为例进行计算，其基本参数如下：太阳轮齿数Zs=10，行星轮齿数Zp=34，模数m=1 mm，压力角α=20°；摆线轮齿数Zc=29，针轮齿数Zb=30，短幅系数K=0.675，偏心距a=0.9 mm，针齿分布圆半径R=40 mm，输入转速为3000r/min，额定负载为58N·m；各构件的转动惯量和质量均利用Pro/E软件经实体造型后得出，构件各刚度的计算方法参照文献[3,9]，其中，啮合刚度均取其相应时变啮合刚度的均值。

经MATLAB编程计算可求得系统的各阶固有频率和振型。限于篇幅，图4只绘出了系统前七阶的固有频率；图5只绘出了太阳轮、2个曲柄轴、行星轮的前4阶振型。

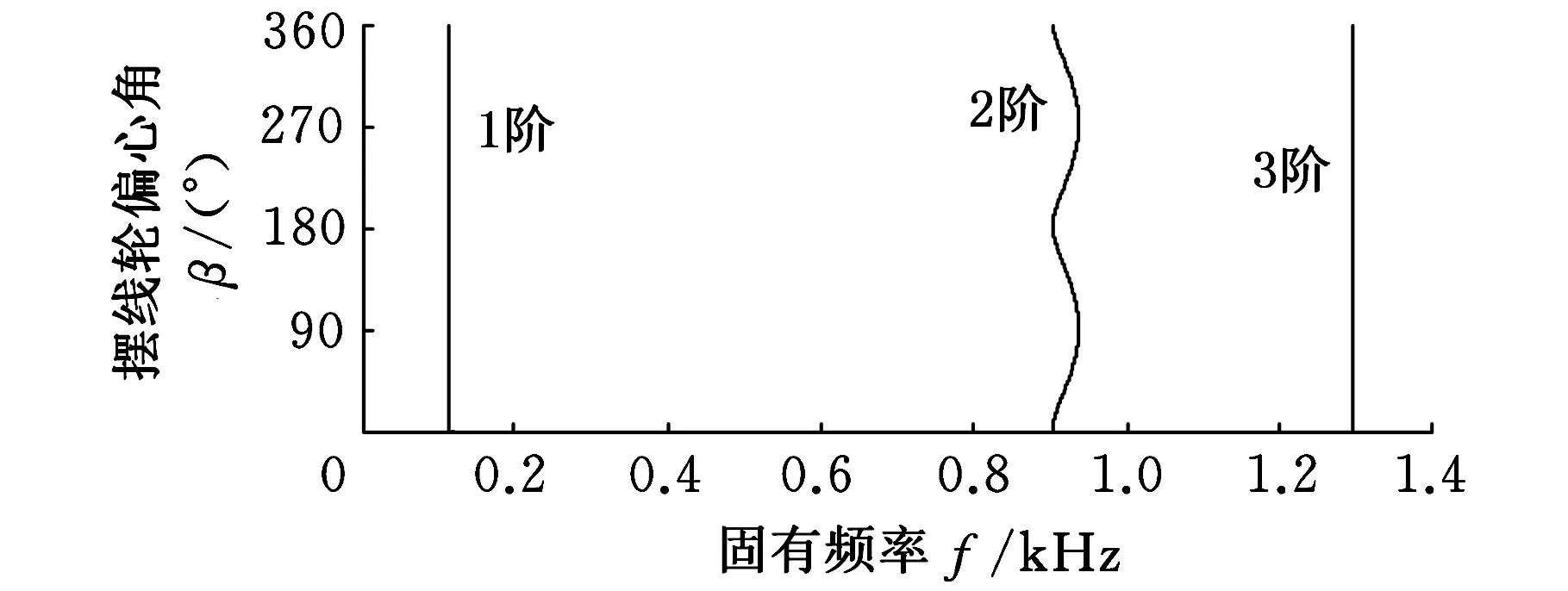
(a)1～3阶振型

(b)4～7阶振型图4　系统前7阶固有频率

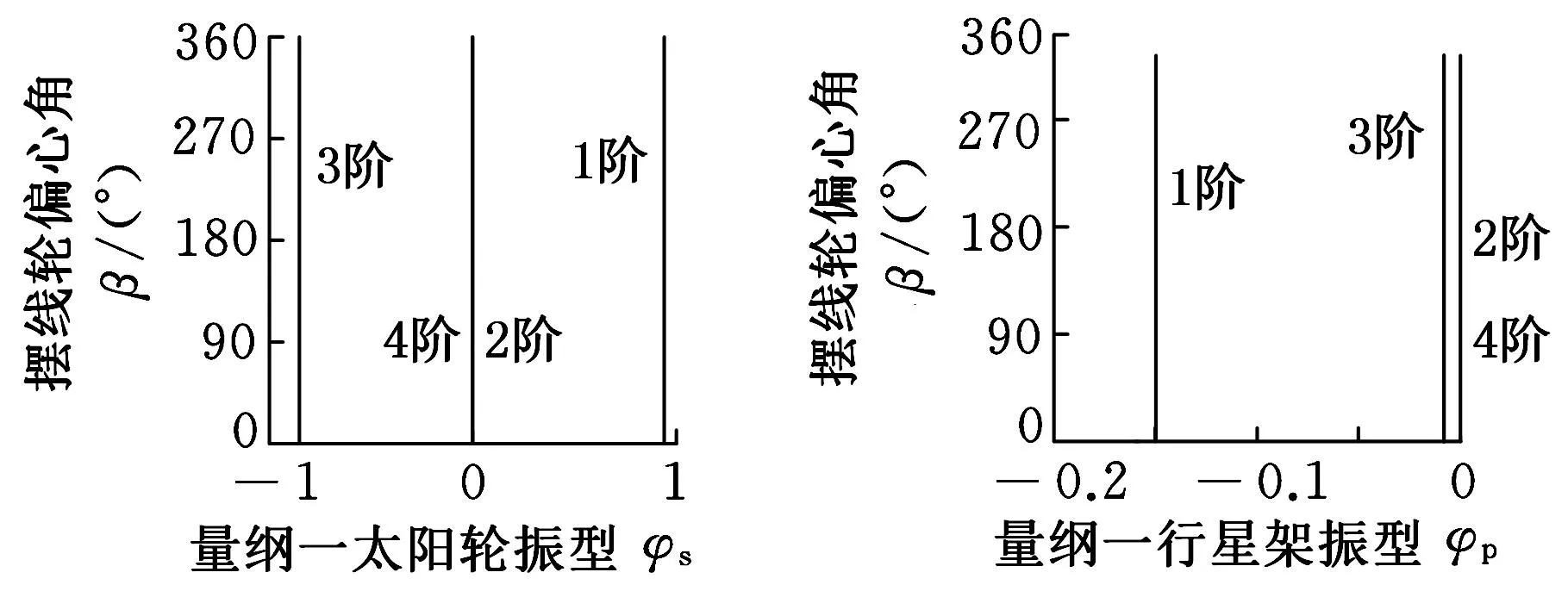
图5　部分构件前4阶振型

计算结果表明，系统奇数阶固有频率不受摆线轮偏心角度周期性变化的影响，为恒值，相应的振型也不受影响；同时，由于系统结构的对称性，导致2个行星轮、2个曲柄轴、2个摆线轮的振型大小相同、方向一致。系统的偶数阶固有频率随着摆线轮偏心角度的周期性变化，呈现出类三角函数的变化规律，相应的振型呈现出行星轮振动模式，即中心类构件，如输入轴、太阳轮、行星架没有振动，振型为零；行星类构件，如行星轮、曲柄轴、摆线轮的振型呈现出余弦函数变化规律，并且两行星轮、两曲柄轴、两摆线轮之间的振型大小相同、方向相反。这种模式表明，摆线轮和曲柄轴的偏心运动只对系统的行星类构件产生影响。这一现象可用行星齿轮相位调谐理论[10]进行物理解释：各构件间的作用力可用傅里叶级数展开为一系列谐波激励。中心类构件仅受到行星类构件的偶数阶谐波激励时，因其结构的对称性，其合力矩为零，处于平衡状态，不产生振动；行星类构件仅受到偶数阶谐波激励，各构件的力矩不为零，且大小相等、方向相反，故而产生方向相反的等幅度扭转振动。

考虑到RV-6型减速器系统的输入转频为50Hz，比计算的系统第一阶固有频率小很多，与高阶频率相差较大，因此采用固有频率测量系统只对系统的第一阶固有频率进行试验测定。用敲击法测得其一阶固有频率为126.9Hz，动力学模型计算结果为121.4Hz，与实验值接近，因此实验结果既验证了修正扭转动力学模型的有效性，又说明系统不会发生共振。

4系统固有频率灵敏度分析

对传动系统进行灵敏度分析可以提高设计效率并降低设计成本，亦可为系统动态特性优化设计提供可靠依据。灵敏度分析方法一般有两种，即伴随结构法和偏导数法。偏导数法[11]是将特征值视为结构参数的多元函数，对其求导而得出灵敏度计算公式的方法。偏导数法数学推导简单，物理概念明确，本文采用此方法。对于系统的正则化振型，满足：

(9)

(10)

(11)

对式(11)进行量纲一化处理可得到量纲一灵敏度：

(12)

对于无阻尼的自由振动系统，结构参数pj可取各构件的转动惯量和刚度。低阶固有频率对系统动态特性影响最大，故对摆线轮偏心角度β=0时系统前4阶固有频率的灵敏度进行分析。通过MATLAB可求得系统固有频率对各构件转动惯量和刚度的灵敏度，用直线分别连接各转动惯量和刚度的灵敏度数值离散点，得到固有频率对转动惯量和刚度的灵敏度曲线。如图6、图7所示。

图6　固有频率对各构件转动惯量的灵敏度

图7　固有频率对各刚度的灵敏度

由图6、图7分析可知，固有频率对行星架和曲柄轴的转动惯量最为敏感。其中，一阶固有频率对行星架转动惯量的敏感度相对较大，设计和优化时，可在保证性能要求的前提下调整其转动惯量，以满足预期动态特性要求。固有频率对支撑轴承和转臂轴承的刚度最为敏感。RV减速器传动过程中，减速器传动比较大，支撑轴承和转臂所受动载荷较大，是系统的薄弱环节，容易因疲劳磨损等原因造成轴承刚度的减小，从而影响系统的固有特性。

为探讨轴承刚度的变化对系统固有频率的影响，以轴承刚度为变量，计算系统固有频率，图8为支撑轴承和转臂轴承刚度的变化对系统一阶固有频率的影响曲线图。

图8　轴承刚度对一阶固有频率的影响

由图8可知，当支撑轴承和转臂轴承因疲劳磨损而刚度减小时，系统一阶固有频率也迅速下降，并不断接近输入转速的频率，引起系统共振。这一结论与实际工况相符。因此，为避免系统发生共振，应适当提高轴承刚度，并对轴承进行合理的工艺处理，增强轴承抗疲劳强度，或者增加曲柄轴的数量，减小轴承的负载，从而延长其有效工作寿命。

5结论

(1)在现有纯扭转振动模型的基础上，进一步计入曲柄轴和摆线轮公转的切向自由度，建立了RV减速器的修正扭转振动模型。

(2)研究了摆线轮偏心角度的周期性变化对系统动态特性的影响，结果表明，摆线轮偏心角度的周期性变化只对系统的偶数阶固有频率及其对应的振型产生影响，偶数阶振型呈现出行星振动模式。

(3)分析了各阶固有频率对转动惯量和刚度灵敏度，结果表明：曲柄轴和行星架的转动惯量、支撑轴承和转臂轴承刚度对系统固有频率影响较大。

(4)轴承因疲劳磨损造成刚度下降，导致系统振动加剧，为优化RV减速器动态特性，应增大轴承刚度或增加曲柄轴数量，改善轴承受力状况。

参考文献：

[1]朱孝录．机械传动设计手册[M]．北京：电子工业出版社，2007．

[2]Mirko B．Analysis of Cycloid Drive Dynamic Behavior[J]．Scientific Technical Review，2009，6(1)：52-56．

[3]张大卫，王刚，黄田，等．RV减速器动力学模型与结构参数分析[J]．机械工程学报，2001，37(1)：69-74．

Zhang Dawei，Wang Gang，Huang Tian，et al. Dynamic Formulation of RV Reducer and Analysis of Structural Parameters[J]．Chinese Journal of Mechanical Engineering，2001，37(1)：69-74．

[4]王刚，赵黎明，王迈．RV减速机动力学建模方法研究与分析[J]．中国机械工程，2002，13(19)：1652-1655．

Wang Gang，Zhao Liming，Wang Mai．Research and Analysis on Dynamics Formulation of RV Reducer[J]．China Mechanical Engineering，2002，12(19)：1652-1655．

[5]严细海，张策，李充宁，等． RV减速机的扭转振动的固有频率及其主要影响因素[J]．机械科学与技术，2004，23(8)：991-994．

Yan Xihai，Zhang Ce，Li Chongning，et al．Natural Frequency of Torsional Vibration of Rotary Vector Reducer and Its Influencing Factors[J]．Mechanical Science and Technology，2004，23(8)：991-994．

[6]Hsieh Chiu-Fan．Dynamics Analysis of Cycloidal Speed Reducers with Pinwheel and Nonpinwheel Designs[J]．Journal of Mechanical Design，2014，136(9)：10.1115/1.4027850.

[7]李充宁，陈晓敏．2K-V型摆线针轮减速机的动力学仿真研究[J]．机械传动，2009，33 (2)：74-77．

Li Chongning，Chen Xiaomin．Study on Dynamics Simulation of 2K-V Cycloid-pin-annulus Reducer[J]．Journal of Mechanical Transmission，2009，33(2)：74-77．

[8]董向阳，邓建一，陈建平．RV传动机构的受力分析[J]．上海交通大学学报，1996，30(2)：65-70．

Dong Xiangyang，Deng Jianyi ，Chen Jianping．Force Analysis of RV Transmission Mechanism[J]．Journal of Shanghai Jiaotong University，1996，30(5)：65-70．

[9]陈忠．滚动轴承及其支承刚度计算[J]．煤矿机械，2006，27(3)：387-388．

Chen Zhong．Stiffness Computation of Rolling Bearing and its Support[J]．Coal Mine Machinery，2006，27(3)：387-388．

[10]Parker R G．Physical Explanation for the Effectiveness of Planet Phasing to Suppress Planetary Gear Vibration[J]．Journal of Sound and Vibration，2000，236(4)：561-573．

[11]傅志方，花宏星．模态分析理论与应用[M]．上海：上海交通大学出版社，2000．

[12]张代胜，王浩．基于灵敏度分析的汽车动力传动系扭转特性优化[J]. 中国机械工程，2013，24(5)：685-689．

Zhang Daisheng，Wang Hao．Optimization of Vehicle Drivetrain Torsional Vibration Characteristics Based Sensitivity Analysis[J]．China Mechanical Engineering，2013，24(5)：685-689．

(编辑张洋)

Analyses of Natural Characteristics and Sensitivity for Torsional Vibration of RV Reducer

Liu BaixiWang WenjunNie Songhui

Xiangtan University，Xiangtan，Hunan，411105

Abstract:Taking the RV reducer as the research object, and considering the influences of the system stiffness and the eccentric angle of cycloid gear on torsional vibration characteristics, a 13 DOF modified torsional dynamics model was established by lumped-parameter method. The impacts of cycloid gear eccentric angle on the natural frequency were analyzed by calculating the natural frequency and corresponding modal shapes of the system. Using the partial derivative method, the sensitivity of natural frequency to moment of inertia and stiffness was calculated. The results show that the key factor influencing the natural frequency is the bearing stiffness.

Key words:rotate vector(RV) reducer; torsional vibration; natural characteristics; sensitivity analysis

收稿日期：2015-03-11

基金项目：湖南省自然科学湘潭联合基金资助项目(14JJ5028)；湖南省教育厅科学研究优秀青年项目(13B115)

中图分类号：TH132．46

DOI：10.3969/j.issn.1004-132X.2016.03.007

作者简介：刘柏希，男，1978年生。湘潭大学机械工程学院副教授。主要研究方向为机构动力学、振动系统建模与分析。发表论文20余篇。王文军，男，1987年生。湘潭大学机械工程学院硕士研究生。聂松辉，男，1968年生。湘潭大学机械工程学院教授。