基于结合部的HSK主轴-刀柄系统动态特性分析
2016-06-23王贵成沈春根郑登升
陈 建 王贵成,3 田 良 沈春根 郑登升
1.江苏大学,镇江,212013 2.成都工具研究所有限公司,成都,6100513.南通理工学院,南通,226002
基于结合部的HSK主轴-刀柄系统动态特性分析
陈建1王贵成1,3田良2沈春根1郑登升1
1.江苏大学,镇江,2120132.成都工具研究所有限公司,成都,6100513.南通理工学院,南通,226002
摘要:建立了HSK主轴-刀柄结合部的有限元模型(FEM),利用弹性理论和黏性阻尼理论辨识结合部内各位置的刚度和阻尼参数。提出将HSK主轴-刀柄系统分为HSK主轴、主轴-刀柄结合部和刀柄三部分:HSK主轴与刀柄简化为多段Timoshenko梁,并使用响应耦合法来计算其频响函数;主轴-刀柄结合部简化为多点弹簧-阻尼模型,采用多点响应耦合法来计算其频响函数;将各个部件的频响函数进行刚性耦合,进而获得基于结合部的HSK主轴-刀柄系统频响函数。分别假定HSK主轴-刀柄结合部为刚性连接、5点弹性连接和7点弹性连接,计算其频响函数,并与实验结果相比较得到相应的结论。
关键词:HSK主轴-刀柄系统;频响函数;结合部;动态特性
0引言
HSK主轴系统(HSK主轴-刀柄-刀具系统)被广泛应用于高速和高精密加工。加工过程中,影响加工质量和加工效率的主要因素为颤振。获得准确的稳定性叶瓣图(切削速度-切削厚度关系图)是避免颤振和保证切削稳定性的必要条件。但无论采用何种方法获得叶瓣图,都需先得到机床主轴系统刀尖点的频率响应函数(FRF)[1]。其中,准确的结合部参数又是精确预测主轴系统刀尖频率响应函数的前提和保证。本文以HSK主轴-刀柄系统为研究对象,先对HSK主轴-刀柄结合部进行参数辨识,再计算基于结合部的HSK主轴-刀柄系统频响函数。
结合部一般都简化为弹簧-阻尼模型。Ozsahin等[2]采用有限差分法和实验测量相结合的方式对刀柄-刀具结合部进行了参数辨识,再利用单点响应耦合法计算其频响函数。此方法只能辨识结合部端点的参数,无法辨识结合部内部各个位置的刚度-阻尼参数。Namazi等[3]采用有限元与实验相结合的方法来辨识结合部参数,并通过有限元法分析其频响函数,此方法只获得了结合部内部各个位置的平动刚度和转动刚度,且其计算量很大,也没有考虑结合部的阻尼参数。程强等[4]基于子结构耦合法和最小二乘法对BT40主轴-刀柄结合部进行了参数辨识,此方法只获得了结合部内部各个位置的平动刚度,没有辨识结合部的转动刚度和阻尼参数。
基于以上方法的优缺点,提出采用有限元法来辨识HSK主轴-刀柄结合部内部各个位置的刚度和阻尼参数,并使用多点响应耦合法来计算HSK主轴-刀柄系统频响函数。
1理论基础
计算HSK主轴-刀柄系统频响函数时,可将系统分为HSK主轴、主轴-刀柄结合部和刀柄三个部分,如图1所示。HSK主轴与刀柄都简化为多段Timoshenko梁,并使用响应耦合法计算其频响函数;主轴-刀柄结合部简化为多点弹簧-阻尼模型,采用基于Timoshenko梁理论的多点响应耦合法来计算相应的频响函数;最终,将各个部件的频响函数进行刚性耦合,进而获得基于结合部的HSK主轴-刀柄系统频响函数。
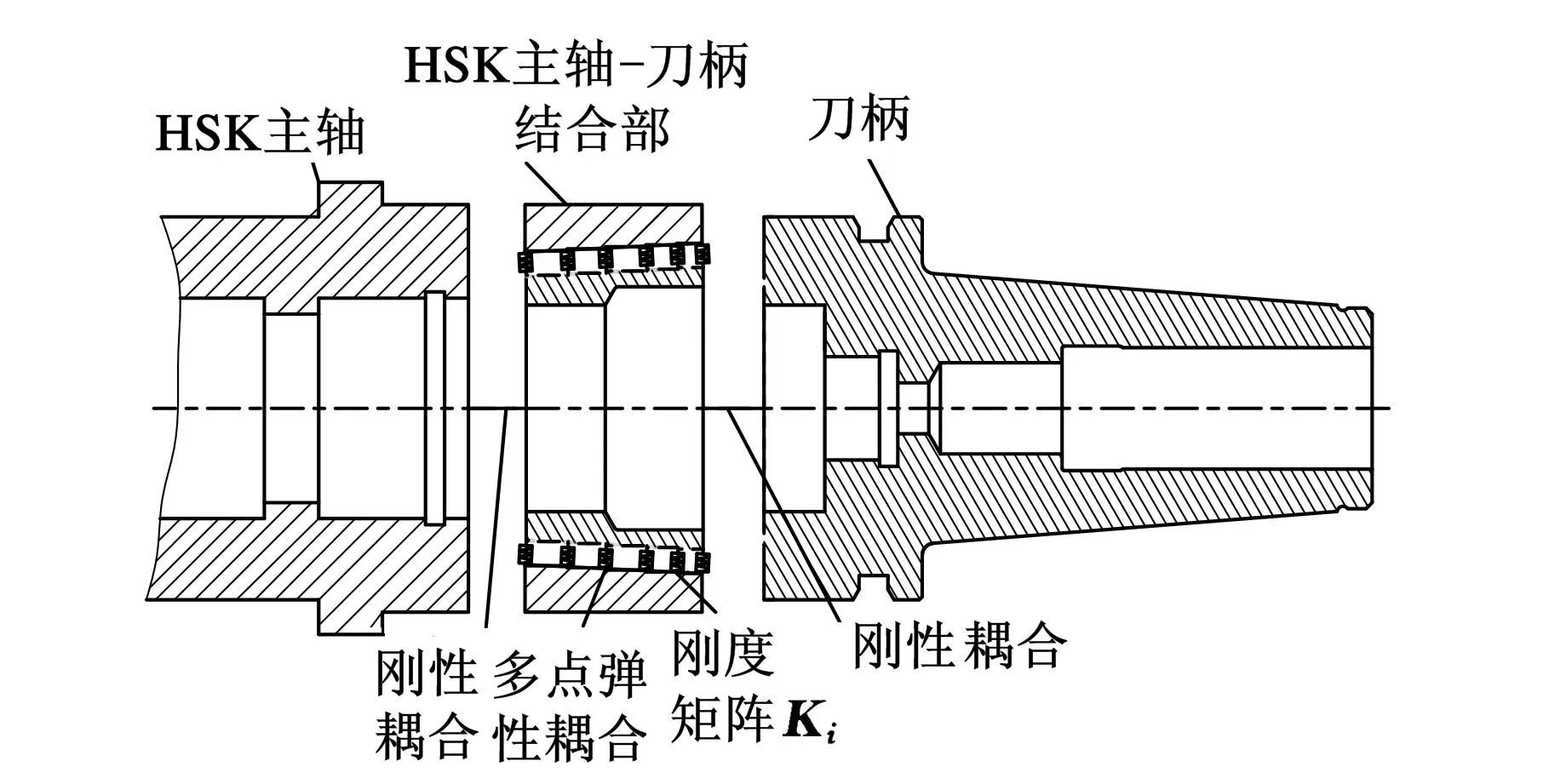
图1 HSK主轴-刀柄系统的理论模型
HSK主轴-刀柄结合部i处的刚度矩阵[5]为

Ki=kyF+iωcyF kyM+iωcyMkθF+iωcθF kθM+iωcθMéëêêùûúú
(1)
式中,kyF、kθF分别为受力载荷下的平动刚度和转动刚度;kyM、kθM分别为受力矩载荷作用下的平动刚度和转动刚度;cyF、cθF分别为受力载荷下的阻尼;cyM、cθM分别为受力矩载荷下的阻尼;ω为角速度。
1.1部件频响函数的理论基础
在计算HSK主轴和刀柄的频响函数时,需将它们都简化为多段Timoshenko梁,先分别计算每段梁的频响函数,再对每段梁进行刚性耦合,进而获得整个部件的频响函数。单段梁频响函数(G11)的计算如图2所示,梁的两端点分别表示为1和2。使用质量集中方程可以建立相应的响应方程,并将与线性和转动位移有关的力和力矩应用到这些点上。点1的响应方程可用H、N、L和P来表示,它们定义如下[6-7]:
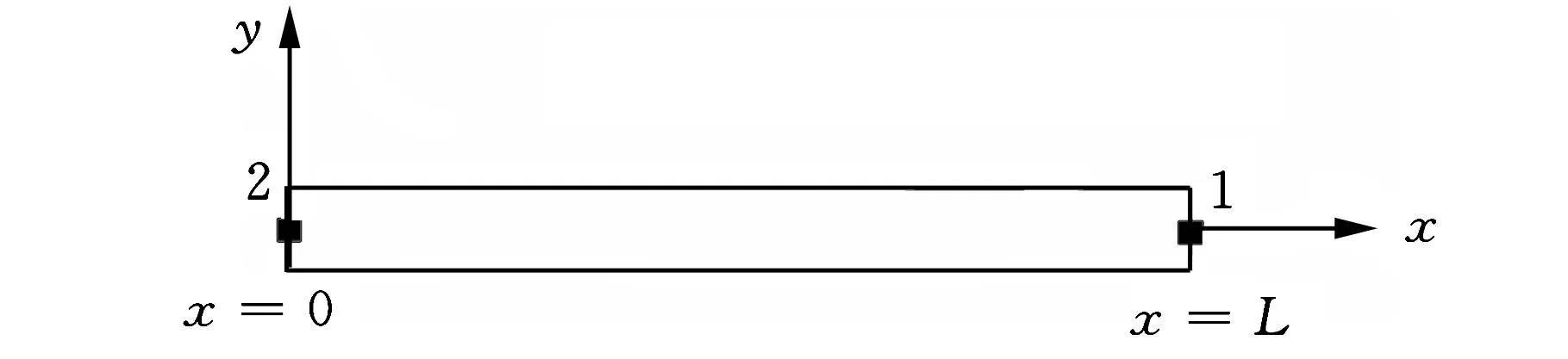
图2 两自由端均匀Timoshenko梁
(2)
其中,y、θ分别表示线性和转动位移,F、M分别表示作用在点上的力和力矩,端点各频响函数可参考文献[1]。
如图3a所示,两段Timoshenko自由端梁可以耦合为一段自由端梁。其中,自由端响应矩阵A和B可以表示为
(3)
A12…B12依A11类推,考虑到连接点的兼容性和连续性,可以得到两段梁的耦合矩阵C[8]:
(4)
同理,可采用相同的方法对多段梁进行刚性耦合,如图3b所示。通过这样的方式,将不同直径和长度的梁进行耦合,可计算得到HSK主轴和刀柄的频响函数,分别为S和H。

(a)两段自由端梁的刚性耦合
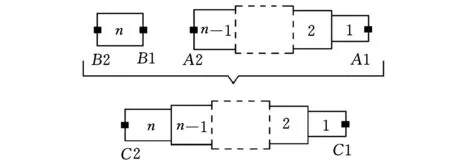
(b)n段梁的刚性耦合图3 多段自由端梁的刚性耦合
1.2主轴-刀柄结合部多点耦合频响函数的理论基础
在主轴-刀柄结合部取3个点,分别为两端点与中心处。结合部的刀柄与刀具都简化为多段Timoshenko梁。当n=3时,总共有6个坐标点,如图4所示,部件(刀具与刀柄)单段的位移/转角可以表示如下[9-11]:
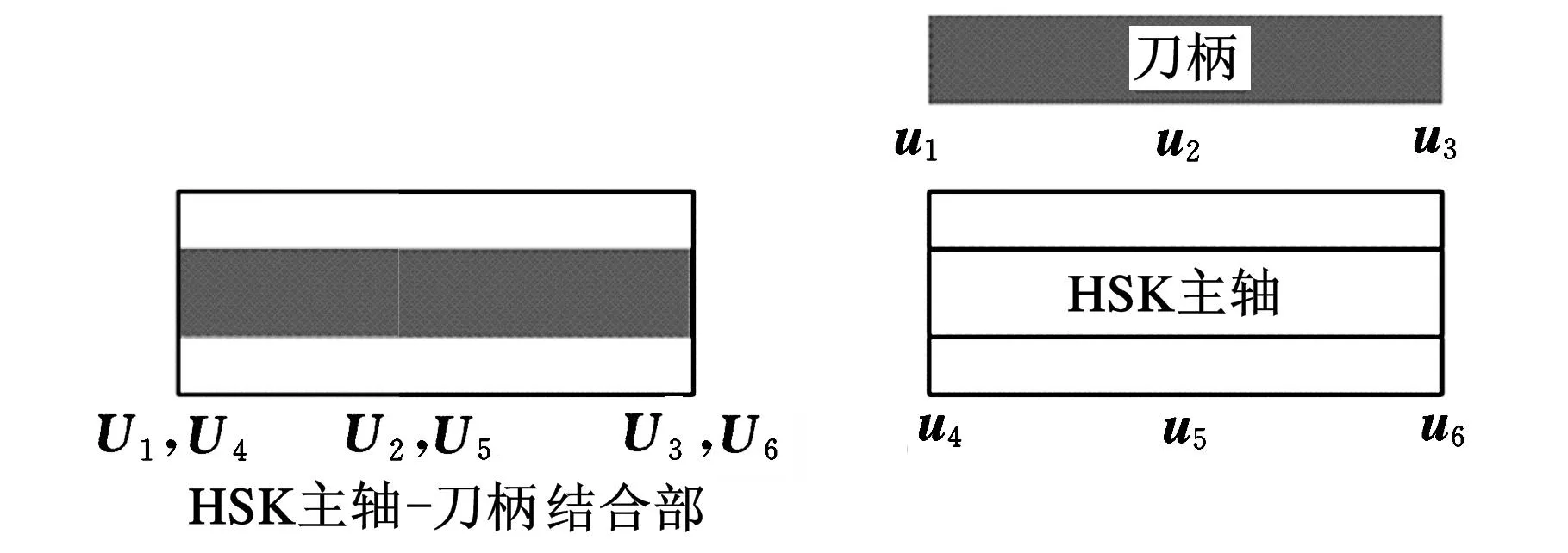
图4 HSK主轴-刀柄系统及部件
(5)
其中,Ri j为刀柄和刀具的频响矩阵,具体形式如式(2)所示;ui=[yiθi]T为位移/转角;qj=[FjMj]T为力/力矩。再根据HSK主轴-刀柄结合部的弹性/阻尼相容性条件和等效方程可得
(6)
(7)
其中,O11为结合部坐标点1处的频响矩阵,Q1为坐标U1的力和力矩,Ki由式(1)给出,并且部件和结合部的坐标相同,ui=Ui,i=1,2,…,6。通过矩阵D可以求得q1/Q1,q2/Q1,q3/Q3。由于结合部的主轴和刀柄都简化为多段Timoshenko梁,因而相应的频响矩阵Rij可通过式(2)~式(6)计算得到。同理,将所获得的单段HSK主轴-刀柄结合部的频响函数进行刚性耦合,最终可获得HSK主轴-刀柄结合部的频响函数。
1.3HSK主轴-刀柄系统频响函数理论基础
将计算得到HSK主轴、HSK主轴-刀柄结合部和刀柄的频响函数进行刚性耦合,进而得到HSK主轴-刀柄系统的频响函数:
(8)
因而,HSK主轴-刀柄系统端点的频响函数为(SOH)11。SO为HSK主轴和HSK主轴-刀柄结合部刚性耦合的频响矩阵,可根据式(5)~式(6)求得
(SOH)11=(SO)11-(SO)12[(SO)22+H11]-1(SO)21=
(9)
2HSK主轴-刀柄结合部的参数辨识
2.1HSK主轴-刀柄结合部的模型
本文主要使用有限元法来辨识结合部内各个位置的刚度和阻尼参数,为简化处理,本文假定cyF=cθF和cyM=cθM[9]。HSK主轴-刀柄结合部规格为A63,主轴和刀柄的材料相同,弹性模量E=500MPa,密度ρ=7850kg/m3,泊松比μ=0.22。并在结合部处设置接触面对,目标面为刀柄外锥面,接触面为主轴内锥面,接触摩擦因数为0.2,过盈量为10μm。在刀柄锥面位置施加18kN的拉紧力,并将主轴末端设置为固定,刀具末端上施加相应的载荷,便可进行热装刀柄-刀具结合部的参数识别。图5所示为HSK主轴-刀柄结合部有限元模型。图6为HSK主轴-刀柄结合部关系示意图。

图5 HSK主轴-刀柄结合部有限元模型
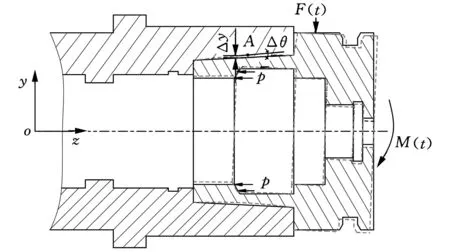
图6 HSK主轴-刀柄结合部关系示意图
本文基于弹性理论来辨识结合部的刚度参数。由图6所示,拉紧力以均布载荷p的形式作用在刀柄上,并在刀柄法兰端面上施加y方向力F(t),主轴-刀柄结合部上沿z方向上任意一点A产生的位移为Δy,A点的刚度为kyF,阻尼为cyF。同样施加力F(t)时,结合面上沿z方向上任意一点A产生的转动角度为Δθ,A点的刚度为kθF。撤去力F(t)后,施加力矩M(t),A产生的位移为Δy,A点的刚度为kyM,阻尼为cyM。同样地施加力矩M(t),A点产生的转动角度为Δθ,A点的刚度为kθM。
2.2HSK主轴-刀柄结合部的刚度辨识
(1)kyF和kθF的参数识别。kyF和kθF为受力载荷下的刚度,分别在模型上施加1500 N、2000 N、2500 N、3000 N和3500 N的作用力。设置相应的参数和求解以后,选取结合部上沿z轴变化的位移Δy,并绘制每一位置的位移-力曲线,斜率即为每一位置的刚度参数kyF,图7a所示为主轴-刀柄结合部沿z轴变化的刚度kyF。通过计算z轴方向相邻两点的位移Δy,可得沿z轴各个位置的转动角度Δθ,绘制每一位置的角度-力曲线,其斜率即为刚度kθF,图7b所示为主轴-刀柄结合部沿z轴变化的刚度kθF。
(2)kyM和kθM的参数辨识。kyM和kθM为受力矩载荷下的刚度,分别在模型上施加力矩10N·m、12.5N·m、15N·m、17.5N·m、20N·m。与上述刚度数据处理方法一样,可得HSK主轴-刀柄结合部沿z轴变化的刚度kyM和kθM,如图7c和图7d所示。
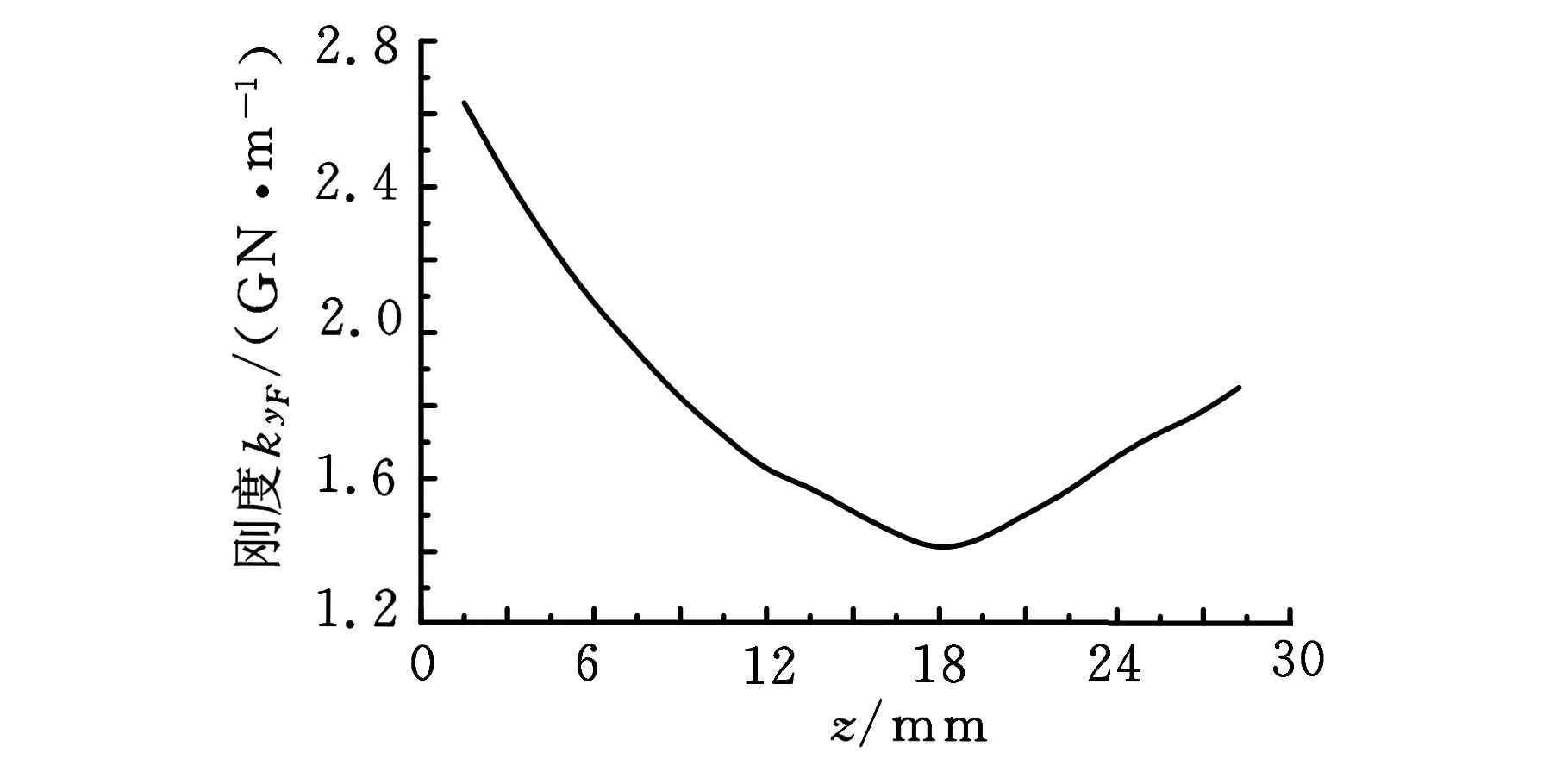
(a)沿z轴变化的刚度kyF
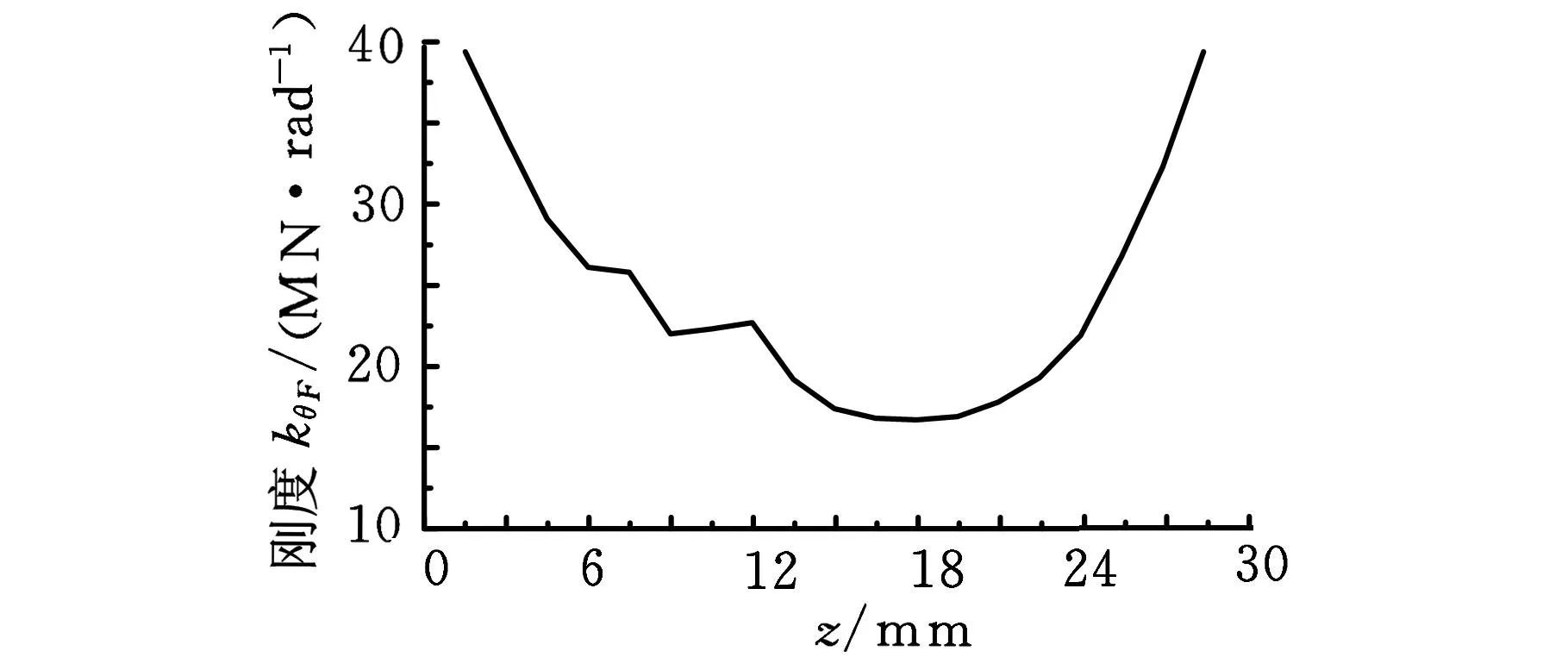
(b)沿z轴变化的刚度kθF
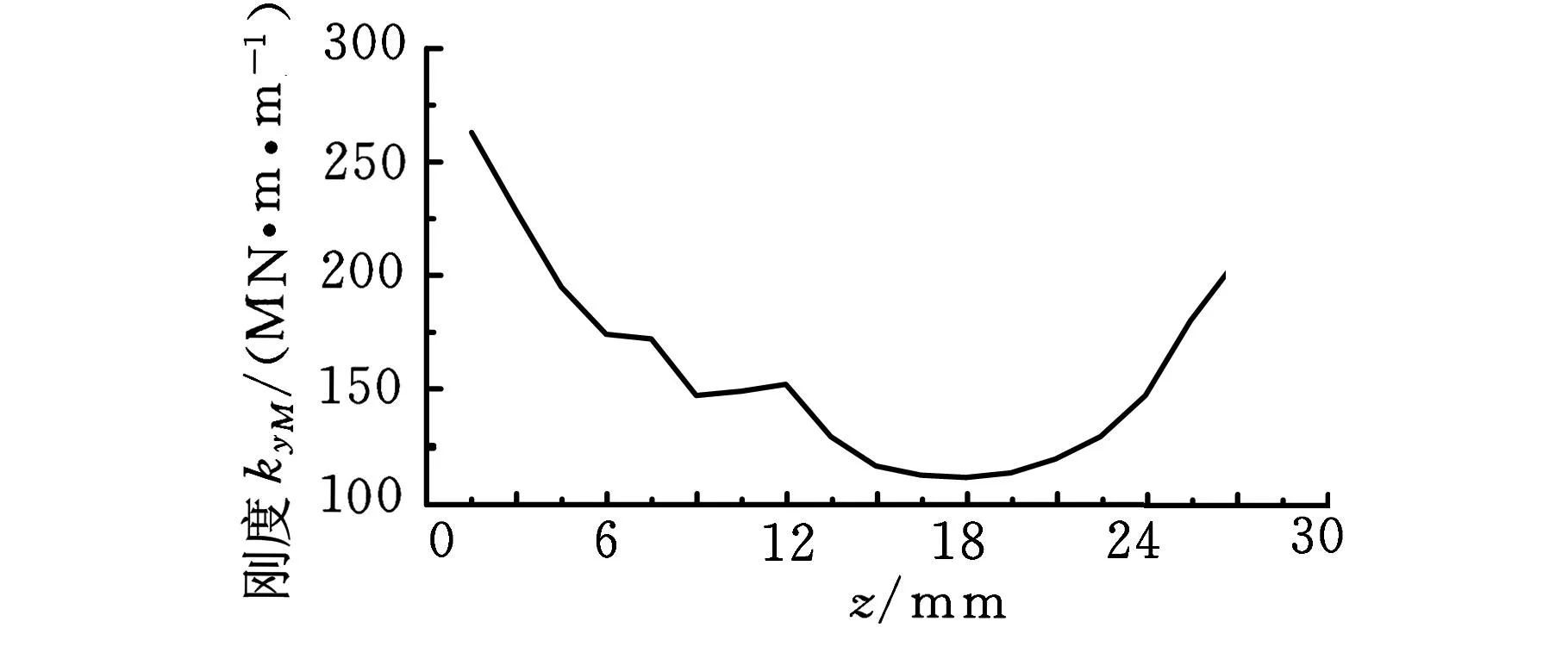
(c)沿z轴变化的刚度kyM
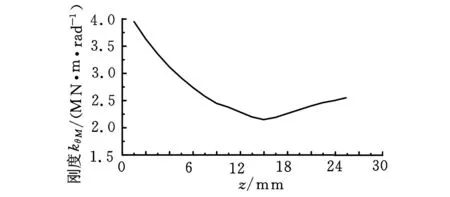
(d)沿z轴变化的刚度kθM图7 结合部沿z轴变化的刚度
HSK主轴-刀柄结合部的4个刚度变化趋势都为两边刚度大,中间刚度最小。由于HSK刀柄为中空薄壁结构,虽然主轴/刀柄为过盈配合,但在拉紧力的作用下使得主轴/刀柄中间部分的接触面积减小,结合部刚度随之降低;又因为HSK主轴/刀柄为锥面和端面同时接触,这使得靠近端面位置的刚度很大。由此可知,拉紧力对HSK主轴-刀柄结合部的刚度影响很大,HSK主轴/刀柄锥面和端面同时接触可提高结合部的刚度,此结论与文献[12-13]所得结论相似。
2.3HSK主轴-刀柄结合部的阻尼辨识
cyF和cyM是由主轴-刀柄结合部在力/力矩的作用下,沿z轴方向产生微小的移动而形成的位移阻尼。将此阻尼等效为黏性阻尼,其计算公式如下[9]:
(10)
式中,Fd,n为每个单元的摩擦阻力;|ln|为结合面每一个接触单元沿z轴方向上滑动位移的绝对值。
与上述刚度识别方法一样,分别在主轴-刀柄结合部模型上施加力和力矩,力为1500 N、2000 N、2500 N、3000 N和3500 N,力矩为10 N·m、12.5 N·m、15 N·m、17.5 N·m和20 N·m。求解以后,分别选取每一接触单元的压力、面积和z轴方向上滑动位移的绝对值,并将其代入到式(10)中可求出相应的阻尼。图8a所示为作用力1500 N和3500 N下的阻尼值与角速度ω的乘积cyFω,图8b所示为力矩10N·m和20N·m下的阻尼值与角速度ω的乘积cyMω。
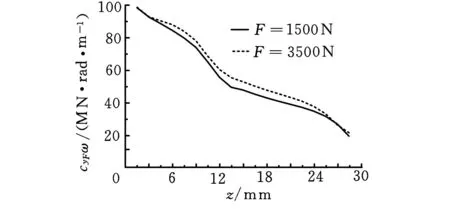
(a)沿z轴变化的cyFω
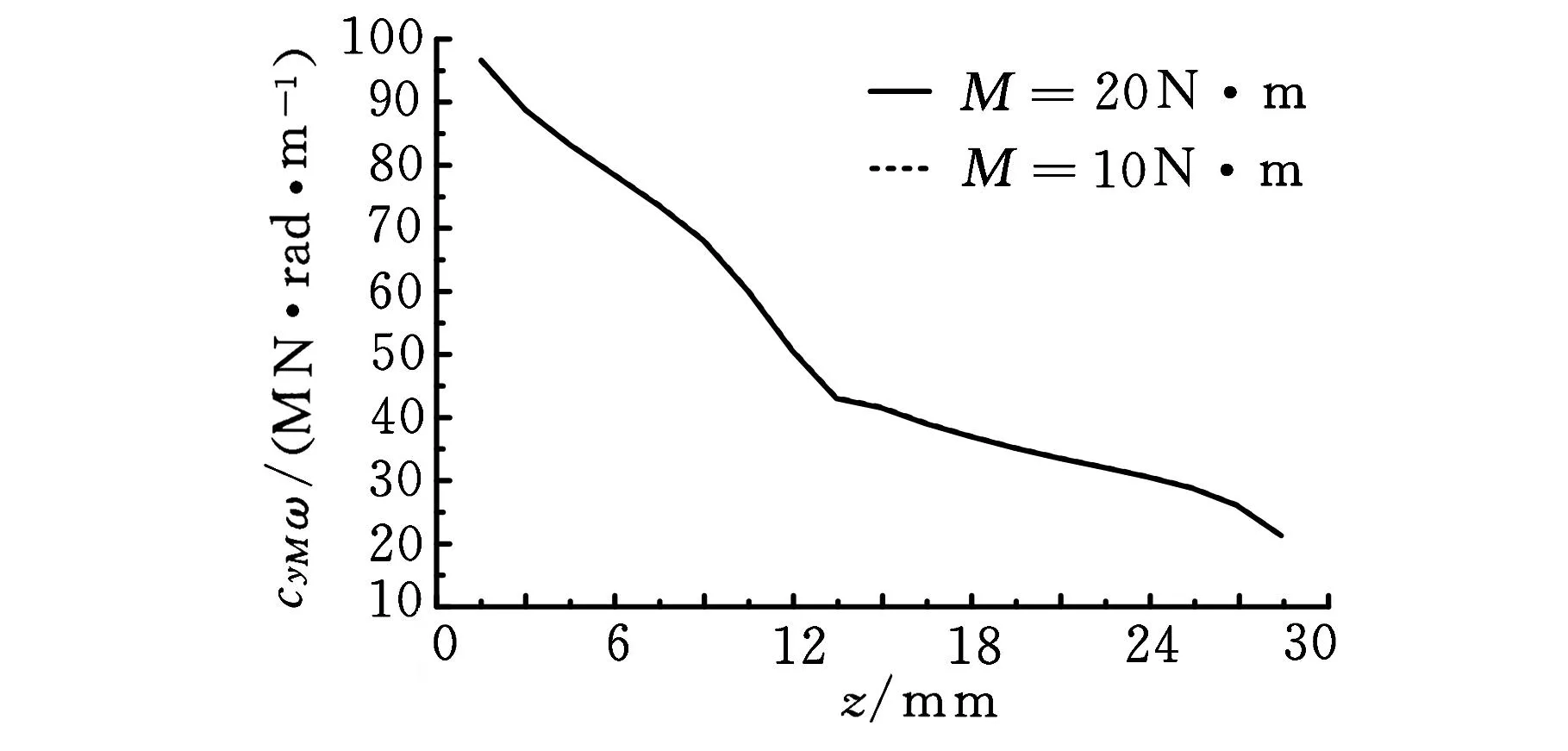
(b)沿z轴变化的cyMω图8 结合部沿z轴的阻尼
3实例分析
3.1HSK主轴-热装刀柄系统端点频响函数

图9 HSK主轴-刀柄系统
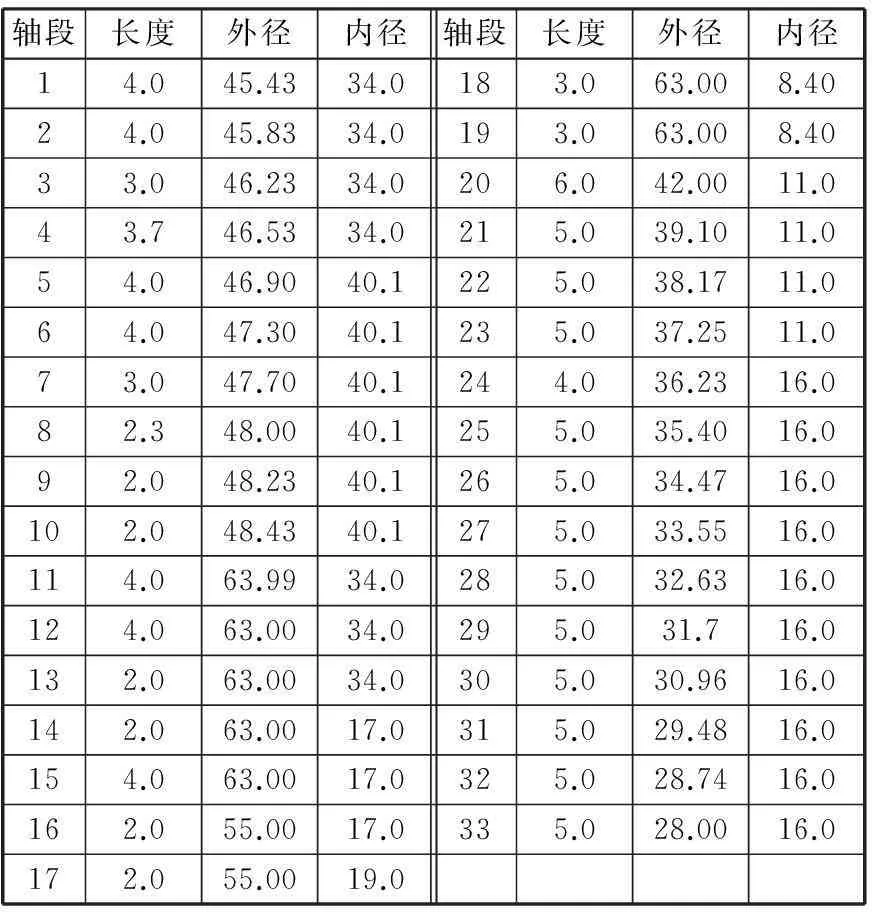
mm
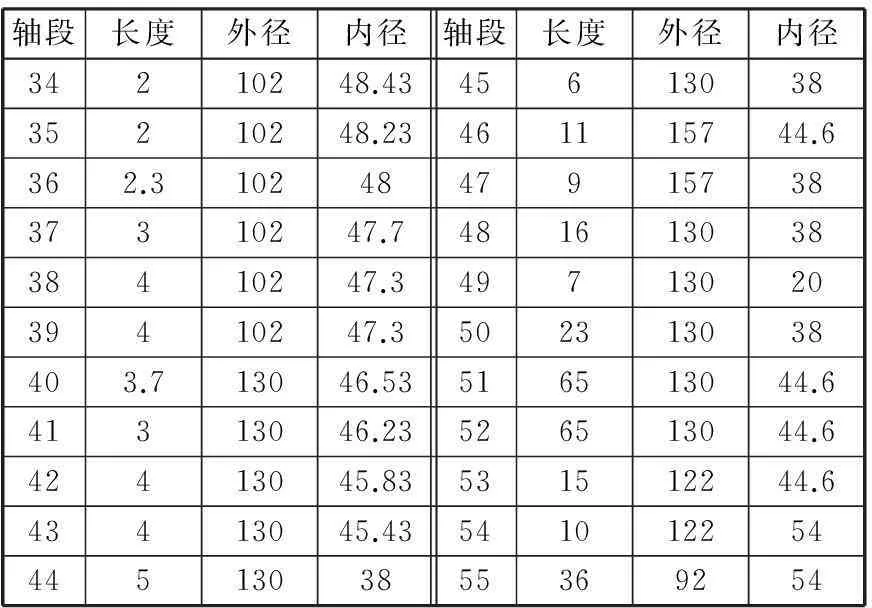
表2 HSK主轴的分段尺寸 mm
3.2实验频响函数
先将HSK主轴-热装刀柄系统置于自由状态;再将Kistler加速度传感器安装在HSK主轴-热装刀柄系统端点上;最后,使用力锤敲击端点处。测量信号通过Cutpro测试系统进行放大、采集和FFT转换,图10为实验频响函数的测量系统图。
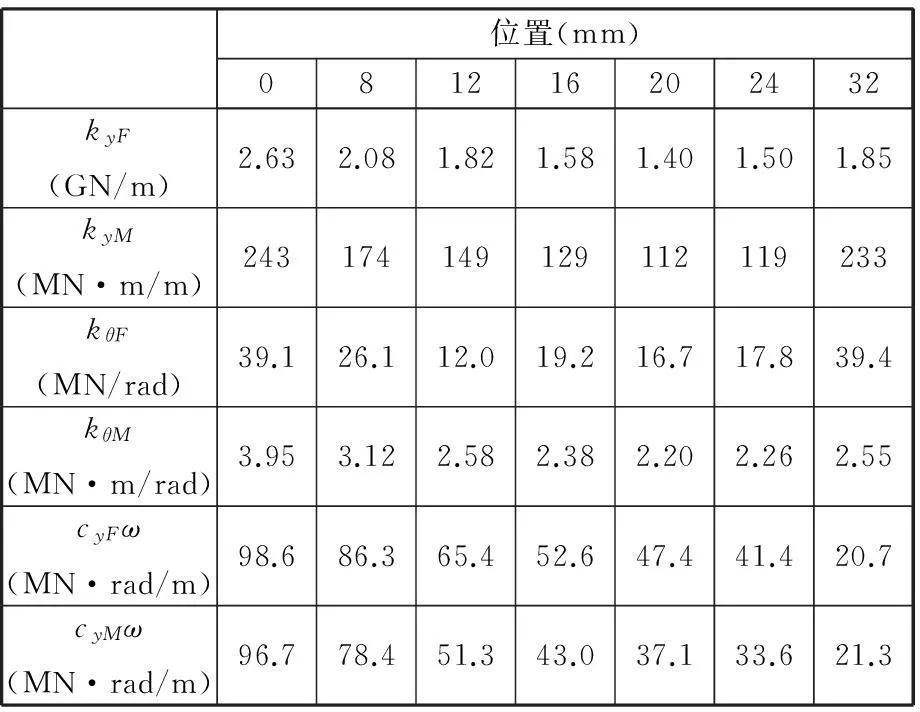
表3 HSK主轴-刀柄结合部内各个位置的参数
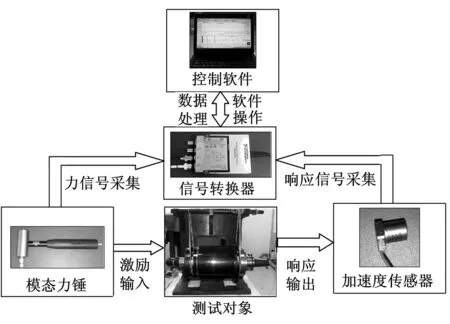
图10 实验频响函数的测量系统图
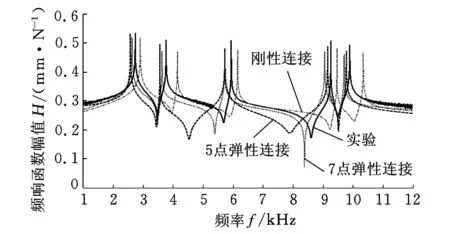
图11 HSK主轴-热装刀柄端点频响函数
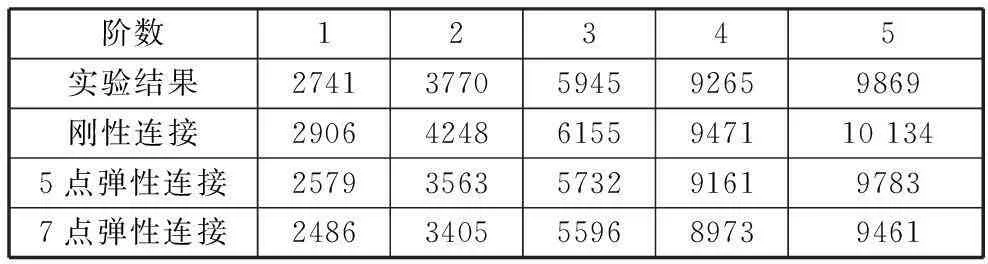
Hz
比较HSK主轴-热装刀柄系统的各阶模态可知,刚性连接的模态比实验模态更大,并且两者最大差值达11.3%,因而不能简单地将HSK主轴-刀柄结合部当作刚性连接来处理。结合部内各点的弹簧-阻尼为并联关系,结合部的整个刚度可等效为各点刚度之和。5点弹性连接计算的模态与实验模态最大差值为5.6%,其差值大的原因就是选取点少,整体刚度低。7点弹性连接计算的模态与实验模态最大差值为4.2%,与实验结果很接近。因此,分析HSK主轴-热装刀柄系统端点频响函数时,需考虑HSK主轴-刀柄结合部的影响,并且选用7点弹性连接来计算系统频响函数更具有合理性。
4结论
(1)建立HSK主轴-刀柄结合部有限元模型,使用弹性理论辨识出HSK主轴-刀柄结合部内各个位置的4个刚度和2个阻尼参数。
(2)基于多点响应耦合法推导出HSK主轴-热装刀柄系统端点频响函数公式,根据此公式分别计算得到HSK主轴-刀柄结合部为刚性连接、5点弹性连接和7点弹性连接的频响函数。并将其模态值与实验值相比较可知,分析HSK主轴-刀柄系统频响函数需要考虑结合部的影响,并且选用7点弹性连接来计算系统频响函数更具有合理性。
参考文献:
[1]Erturk A,Ozguven H N,Budak E.Analytical Modeling of Spindle-tool Dynamics on Machine Tools Using Timoshenko Beam Model and Receptance Coupling for the Prediction of Tool Point FRF[J].International Journal of Machine Tools & Manufacture,2006,46:1901-1912.
[2]Ozsahin O,Erturk A,Ozguven H N,et al. A Closed-form Approach for Identification of Dynamical Contact Parameters in Spindle-holder-tool Assemblies,International Journal of Machine Tools & Manufacture,2009,49:25-35.
[3]Namazi M,Altintas Y.Modeling and Identification of Tool Holder-spindle Interface Dynamics[J].International Journal of Machine Tools & Manufacture,2007,47:1333-1341.
[4]程强,刘新宇,赵永胜.基于频响函数的主轴-刀柄结合部参数辨识方法[J].北京工业大学学报,2013,39(8):1144-1147.
Cheng Qiang,Liu Xinyu,Zhao Yongsheng.Identification of Dynamical Contact Parameters for Spindle-tool Holder Interface Based on Frequency Response Functions[J].Journal of Beijing Technology University,2013,39(8):1144-1147.
[5]Budak E,Ertürk A.A Modeling Approach for Analysis and Improvement of Spindle-holder-tool Assembly Dynamics[J].Annals of the CIRP,2006,56:1235-1239.
[6]Erturk A,Ozguven H N,Budak E.Effect Analysis of Bearing and Interface Dynamics on Tool Point FRF for Chatter Stability in Machine Tools by Using a New Analytical Model for Spindle-tool Assemblies[J].International Journal of Machine Tools & Manufacture,2007,47:23-32.
[7]楼梦麟,任志刚.Timoshenko简支梁的振动模态特性精确解[J].同济大学学报,2002,30(8):911-915.
Lou Menglin,Ren Zhigang.Precise Solution to Modal Characteristics of Timoshenko Pin-ended Beams[J].Journal of Tongji University,2002,30(8):911-915.
[8]Park S,Altintas Y,Movahhedy M.Receptance Coupling for End Mills[J].International Journal of Machine Tools & Manufacture,2003,43:889-896.
[9]Schmitz T L,Powell K,Won D.Shrink Fit Tool Holder Connection Stiffness/Damping Modeling for Frequency Response Prediction in Milling[J].International Journal of Machine Tools & Manufacture,2007,47:1368-1380.
[10]Filiz S,Cheng C H,Powell K B,et al.An Improved Tool-holder Model for RCSA Tool-point Frequency Response Prediction[J].Precision Engineering,2009,33:26-36.
[11]Schmitz T L,Duncan G S.Receptance Coupling for Dynamics Prediction of Assemblies with Coincident Neutral Axes[J].Journal of Sound and Vibration,2006,289:1045-1065.
[12]Hanna I M,Agapiou J S.Modeling the HSK Toolholder-spindle Interface[J].Transactions of the ASME,2002,124:734-744.
[13]Agapiou J S.A Methodology to Measure Joint Stiffness Parameters for Toolholder-spindle Interface[J].Journal of Manufacture System,2005,24:13-20.
[14]陈建,王贵成.HSK 热装刀柄的加热性能分析[J].中国机械工程,2013,24(12):3235-3239.
Chen Jian,Wang Guicheng.Heat Performance Analysis of HSK Shrink Toolholder,China Mechanical Engineering,2013,24(12):3235-3239.
[15]王贵成,王树林,董广强.高速加工工具系统[M].北京:国防工业出版社,2005.
(编辑袁兴玲)
Dynamic Property Analysis of HSK Spindle-toolholder System Based on Joint Part
Chen Jian1Wang Guicheng1,3Tian Liang2Shen Chungen1Zheng Dengsheng1
1.Jiangsu University,Zhenjiang,Jiangsu,212013 2.Chengdu Tool Research Institute Co., Ltd.,Chengdu,610051 3.Nantong Institute of Technology,Nantong,Jiangsu,226002
Abstract:The HSK spindle-toolholder FEM was modeled and the stiffness and damp parameters of joint part were identified with elastic theory and damp theory.The HSK spindle-toolholder system could be divided into three parts,such as HSK spindle,spindle-toolholder joint part and toolholder. HSK spindle and toolholder could be simplified as Timoshenko beam, and the FRF could be gained with receptance coupling theory.The spindle-toolholder joint part might be simplified as spring-damp model,and the FRF could be achieved with multi-points receptance coupling theory. Then the FRF of system was gained with rigid coupling theory.The spindle-toolholder was treated as rigid connection,five-points connection and seven-points connection,and the tip-point FRFs of system were computed.At last, comparing these FRFs with experimental FRF, some results may be obtained.
Key words:HSK spindle-toolholder system;frequency receptance function(FRF);joint part;dynamic performance
收稿日期:2014-12-17
基金项目:国家科技重大专项(2013ZX04009031)
中图分类号:TG504
DOI:10.3969/j.issn.1004-132X.2016.03.003
作者简介:陈建,男,1987年生。江苏大学机械工程学院博士研究生。研究方向为高速加工工具系统。王贵成(通信作者),男,1955年生。江苏大学机械工程学院教授、博士研究生导师,南通理工学院副校长。田良,男,1961 年生。成都工具研究所有限公司副总工程师。沈春根,男,1969 年生。江苏大学机械工程学院副教授、博士。郑登升,男,1989年生。江苏大学机械工程学院硕士研究生。
