自旋波在十字交叉形磁性纳米线中的微磁模拟研究

张佳超 王瑞方

摘要：由铁磁性纳米线组成的自旋波导线路将不可避免地发生线路交叉。在交叉区域磁矩呈现明显不均匀分布，它对自旋波的散射作用可以等效地视为一个自旋波“势垒”。文章通过微磁模拟方法研究了在不同交变频率外场激发的自旋波在十字交叉形坡莫合金纳米线中的传播特性，发现势垒对自旋波传播的影响与场源频率有关。

关键词：自旋波；十字交叉形；磁性纳米线；势垒；微磁模拟 文献标识码：A

中图分类号：TQ31 文章编号：1009-2374（2016）17-0013-03 DOI：10.13535/j.cnki.11-4406/n.2016.17.006

1 微磁模拟

我们设计的十字交叉纳米线如图1（a）所示。底部的坡莫合金纳米线（以下简称L1）长l1为3000nm，宽w1为100nm，厚度h1为5nm。在x=1500nm处，在L1上叠放一个长度l2=200nm、宽度w2=10nm、厚度h2=10nm的坡莫合金纳米线（以下简称L2）。两条纳米线夹角为90度。我们设置纳米线L1的初始态磁矩沿+x方向，而纳米线L2中磁矩沿+y方向。然后样品在零场条件下弛豫到稳定状态。达到稳态时，纳米线L1中心区域的磁矩分布如图1（b）所示。在以交叉部位为中心、宽度约200nm范围内形成了一个磁畴壁（如图中虚线区域所示）。我们利用微磁模拟软件LLG Simulator对样品的磁矩动力学进行数值计算。计算中材料的磁性参数设置为坡莫合金的常用值，即交换作用常数Aes=1.3×1011J/m、饱和磁化强度Ms=800×10-3A/m、吉尔伯特衰减常数α=0.01、磁晶各向异性为零。元胞尺寸为2.5×5×5nm3。在纳米线L1两端250nm区域内，阻尼常数α从0.01逐渐增加到1，以避免自旋波在纳米线边界的反射。

2 结果

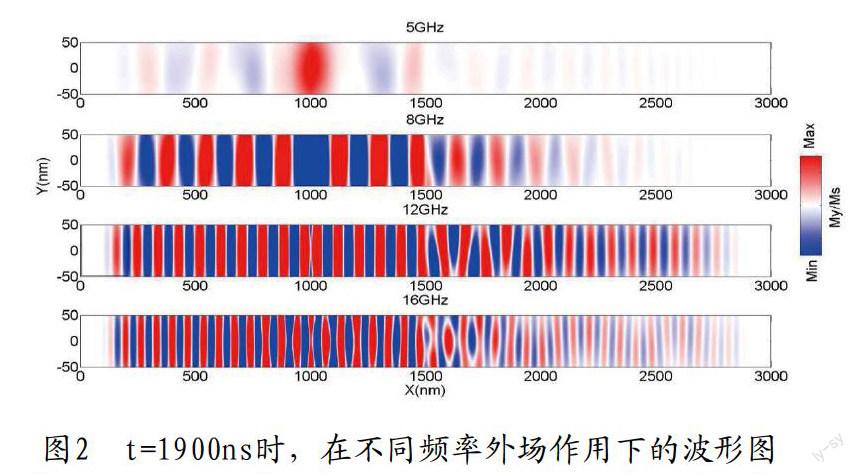
为了观察自旋波在不同频率下的传播图样，我们在处施加方向的局域振荡磁场以激发自旋波。其中，激励场振幅H0=500oe，总模拟时间设定为2ns，激励场频率范围为5～20GHz。当波源频率高于纳米线L1的截止频率时，自旋波向波源两边分别沿+x和-x方向传播。经过1.9ns的传播之后，自旋波的波形逐渐达到稳定，如图2所示：

图2显示当自旋波频率f=5GHz时，自旋波很难在纳米线中传播，磁矩振荡局限在波源处。当频率增加至f=8GHz时，自旋波可以在纳米线中较为稳定地传播，并保持较好的波形。自旋波在传播过程中由于坡莫合金的阻尼作用，使得振幅随传输距离延长而不断衰减。当自旋波频率增加至f=12GHz时，穿越势垒的波形发生了明显扭曲，自旋波以“之字形”状态向前传播。

低频情况下，波源只激发了基态n=1，自旋波可以在纳米线中较为稳定传播。

而在高频时，场源除了可以激发基态n=1，还可以激发更高阶的对称模态（如n=3等），这些对称模态之间会产生自聚焦现象。当自聚焦自旋波到达势垒时，就会激发偶数模态（如n=2，4等）。所以在势垒后（即3000nm>X>1500nm）至少存在三种模态，不同模态之间会发生干涉。

3 分析与讨论

为了研究这些模态是如何形成的，我们得到了纳米线中自旋波的色散关系曲线，如图3所示。

如图3（a）所示，在势垒之前自旋波的振动模式为的奇数模态，截止频率分别为6.8GHz，15.5GHz，27.5GHz，43.8GHz。而在势垒之后，出现奇数模态的同时，偶数模态也被激发。图3（b）中11.1GHz，25.2GHz，35.7GHz分别对应于n=2，4，6模态的截止频率。

值得注意的是，模态的阶数越高即n越大，则对应模态的截止频率就越高。在低频段，场源仅激发了n=1模态，自旋波可以在纳米线中较为稳定地传播。中频段，场源仍然只激发了n=1的模态，但自旋波在势垒区域受到散射并激发出了n=2模态。因此在势垒之后的波是对L1中线（y=0）对称的n=1模态和非对称的n=2模态的叠加，从而发生自旋波波形扭曲。而在高频段，更高阶的模态被激发，不同模态间相互叠加，形成了干涉图样（如图2中16GHz时的传播图样）。

纳米线中，不考虑衰减，第n阶模态的磁矩振幅的空间分布可以表示为：

式中：是纳米线的有效宽度；表示波源激发频率；为该频率下激发的n阶模态的自旋波轴向传播波矢；为激发波源的初始相位；是相对励磁效率。取在一个周期内取平均值，可以得到第n个模态的强度分布。以f=16GHz，为例，得到模态n=1和n=3的强度分布，如图4（a）、（b）所示。不同模态间会叠加，振幅的空间分布可以表述为：

不考虑波强的衰减，从理论上得到的波强分布如图4（c）所示，而微磁模拟得到的纳米线波强分布如图4（d）所示，可以看到两者大致吻合。这说明波源激发的波包含两种模态n=1和n=3。同样f=12GHz时，当自旋波通过势垒可以激发n=2的非对称模态。对比微磁模拟结果，得到如图4（e）、（f），两者大致也吻合。这恰恰也说明，在图2中看到的中高频段波形的扭曲，是由于对称模态和非对称模态之间的叠加，从而使自旋波以“之字形”状向前传播。

另外，图2显示当外加场源的频率不同时，经过势垒之后的自旋波的振幅也发生了不同的变化。当自旋波传播到势垒区域时，一部分波会被势垒所反射；另一部分自旋波则会发生透射，继续向+x方向传播。不同频率下，自旋波穿透势垒的能力不同。如图5所示为透射系数和反射系数与频率f之间的关系。反射系数和透射系数可通过下式得到：

式中：MI为自旋波在穿过势垒前的入射振幅；MT为自旋波穿过势垒时的透射振幅；MR为被势垒反射的自旋波振幅。计算多个时刻的反射系数和透射系数，并取平均值得到和。由图5所知，在f=12GHz时透射系数最大，接近等于1；在f=17GHz时，透射系数最小。从计算结果看，。

同时我们发现磁畴壁的宽度随着频率也是振荡变化的。磁畴壁的宽度可以表示为：

式中：L1、L2分别表示磁畴壁左右边界所在的位置。

我们设定Mx=0.95的位置为磁畴壁边界。在特定频率的交变外场的作用下，一开始，自旋波还未传播到势垒区域，所以畴壁宽度保持不变。当自旋波传播到势垒区域之后，畴壁的边界位置随之发生振荡，因此根据式（4）畴壁宽度也随时间发生振荡。磁畴壁存在两种不同的振荡模式。在f=11GHz，畴壁左右边界以相同相位振动；而在场源频率在17GHz时，左右边界呈反相振动。磁畴壁的两种振荡模式可能会影响自旋波在势垒处的反射系数和透射系数，但这背后的物理机制尚待进一步的研究。并且随着外加场源频率的增加，畴壁宽度振幅逐渐减小。这是因为随着频率增大，磁振子的能量越大，从而势垒对自旋波的阻碍作用相对较小而造成的。

4 结语

我们采用微磁模拟方法研究了自旋波在十字形坡莫合金纳米线中的传播特性。低频波源仅激发出n=1的模态，自旋波可以在纳米线以稳定波形传播。高频自旋波在受到十字交叉区域的势垒散射作用后，激发出偶数模态使得透射出去的自旋波以“之字形”传播。我们还研究了不同频率下自旋波在势垒处的反射系数与透射系数，发现在f=12GHz时透射系数最大，而f=17GHz时透射系数最小。在自旋波作用下畴壁区域产生两种振荡模式，一种为左右边界同相振动，另一种为左右边界反相振动。自旋波透射系数与频率的关系以及它和畴壁振动模式间的关系的物理机制尚待进一步研究。

参考文献

[1] V.V.Kruglyak，et al.J.Phys.D：Appl.Phys.43，264001，2010.

[2] A.Khitun，et al.J.Phys.D：Appl.Phys.43，264005，2010.

[3] Hertel，R.，Wulfhekel，W.&Kirschner，J.Domain-wall induced phase shifts in spin waves.Phys.Rev.Lett.93，257202，2004.

[4] Schneider，T，et al.Realization of spin-wave logic gates.Appl.Phys.Lett.92，022505，2008.

[5] International Technology Roadmap for Semiconductors（ITRS）2009 edition.Emerging Research Devices，2009.

作者简介：张佳超（1990-），女，浙江绍兴人，厦门大学物理与机电工程学院在读硕士，研究方向：低维磁性纳米材料。

（责任编辑：黄银芳）