基于风险承担能力的协同创新风险分担方法研究*
2016-06-20李林,王鲁
李 林,王 鲁
(湖南大学 工商管理学院,湖南 长沙 410082)
基于风险承担能力的协同创新风险分担方法研究*
李林,王鲁
(湖南大学工商管理学院,湖南长沙410082)
摘要:通过三角模糊层次分析法(TF-AHP)衡量协同创新项目中风险承担组合的风险承担能力,并以此为依据。利用Shapley值法确定开展协同创新项目时每个合作方的风险承担能力贡献值,最终根据此风险承担能力贡献值的大小来据制定风险分担比例的思路,为协同创新过程中确定分担风险投入比例提供一种新思路。
关键词:协同创新;风险承担能力;风险分担;三角模糊层次分析法(TF-AHP);Shapley值法
一、引言
协同创新已经成为一种具有较高自主创新能力的全新组织模式,为了在决策过程中确保合作各方的利益需求,保持合作各方的积极性,迫切需要制定一种客观准确并被普遍接受的风险分担方法,来确保协同创新各方的利益均衡。目前,国内外学者对风险分担的研究主要集中在定性研究和风险理论的完善方面,如Yeo(2000)等[1]257-268和Jin(2008)等[2]707-721分别采用了案例分析和实证调研等方法构建了风险分担矩阵,并定性分析了基于合同的风险分配机制。Khazaeni(2012)等、[3]789-800Lam(2007)等、[4]485-493Xu(2012)[5]894-903等运用模糊推理的相关方法构建风险分配的指标体系,并重点分析了各级指标对风险分担绩效的权重。戴建华(2004)等[6]33-36在研究协同创新项目利益分配的过程中,考虑了风险因素的影响,提出了一种基于风险因子的修正方法,对Shapley值法进行了相应的改进,并且分析了Shapley值法的优势与不足,强调每个合作方在面对风险时表现出的差异性。李林(2015)等[7]64-68将风险因素单独研究,将协同创新的多主体性、协同性、动态性等特点考虑在内,采用合作博弈的概念以确定各方的承担比例。上述方法为解决协同创新风险分担提供了思路,但若要使其运用在实际决策过程中则需要大量项目数据和风险数据作为基础。由于风险的多样性,复杂性以及协同创新项目独特性的影响,即使同一种风险,也将因所发生的项目不同而发生变化,因此很难将以往的统计数据作为分担风险的依据。介于以上分析,本文提出一种客观准确并能被普遍接受的风险分担方法,即采用TF-AHP来估计各个风险承担组合的风险承担能力,并利用Shapley值法确定各合作方的风险承担能力贡献值,将参与协同创新的各合作方对风险承担能力贡献值作为分担风险的依据,以此确定风险分担比例。以风险承担的能力作为切入点,避免了使用确定性较大的风险本身作为分担依据,取而代之以确定性较大的合作方风险承担能力作为依据,大大提高了风险分担的客观性和准确性。
二、建模理论基础及方法优势
(一) 基于三角模糊层次分析法(TF-AHP)的风险承担能力量化方法
随着层次分析法的评价方式的成熟,其在评价不确定性问题时可起到很好效果。[8]156-158模糊层次分析法是基于层次分析法衍生出的一种改进方法,将人判断的模糊性纳入评价中,使结果更具有说服力。[9]148-153三角模糊层次分析法(TF-AHP)是在模糊层次分析法的基础上加入了三角模糊数学的概念,让专家给出三个分值,分别为最悲观估计,最大可能估计和最乐观估计。通常专家在进行打分时使用“大约”、“左右”、“上下”等语言来回答所提出的问题。
采用TF-AHP构建模型可以使评估更契合专家评判标准,有效地降低误差,从而增加风险承担能力量化的准确性。对于个体或组织,其承担和控制某个风险的能力的度量是很难用一个数值精确表达的,因此考虑人判断的模糊性很有必要。
(二) 基于Shapley值法的风险分担策略
沙普利值(Shapley)是由美国经济学家Shapley提出来的,用于解决多人合作对策问题的一种数学方法。范如国(2006)[10]127在研究中提出Shapley值法相较于合作博弈另外两个解法概念——核心和稳定集而言,有两大优点。首先,它必然存在,其次,其解答是唯一的。已有的相关研究主要是利用其解决合作博弈的利益分配问题。而风险承担能力的变化也可看作是通过合作而带给各个合作方的一种效益。因此,将此方法用于风险分担问题在理论上是可行的。
采用Shapley值法构建风险分担模型的意义在于使分担比例更加客观,经此法最终得到的风险分担比例是由每个合作方对风险承担组合的贡献大小来确定的。因此,对风险承担的效率性更强,同样也能满足成员对于公平性的要求。
(三) 风险分担模型构建思路
风险承担比例是影响利益均衡的一个重要因素,在合作过程中合作各方必然要求己方获得客观合理的风险分担比例。各合作方及其组合对风险的承担大小的贡献度在一定程度上反映出其在面临风险时的获益能力、控制风险能力以及所能承受的风险上限。在协同创新项目开展过程中,贡献较强的合作方在风险中的损失较少,对风险的应对能力也相对较强,风险上限也较风险承担能力较低的合作方要高,因此贡献较强的合作方相应地加大风险承担的比例,既不会对效益值带来较大损失,也能实现风险的有效控制,同时还能维持贡献较低的合作方的积极性,从而维持整个协同创新项目的顺利进行。因此,协同创新的合作过程中各合作方对风险承担能力的贡献可作为协同创新项目中各方分担风险比重的依据,以此来分担风险满足风险分担原则,更有利于联盟的稳定性。
要明确各个成员的风险分担比例,首先要利用TF-AHP确定各个成员以及其组成的可能组合的风险承担能力,再利用Shapley值法求出每个成员对联盟对某一风险的承担能力的贡献值,按贡献值比例确定各个合作方的风险分担比例,理论模型如图1。

图1 理论模型图
(四) 模型优势分析
在项目管理中,风险分担比例的确定主要从三个方面着手:第一,从风险自身着手,通过系统地收集和分析相关风险的数据,得到风险分担比例;第二,从利益均衡的角度,以各合作方未来预期从项目中获得的收益作为分担风险的依据,按股分担是其中一种较为常见的方法;第三,谈判。即合作方之间通过沟通、协商、谈判等方式制定出普遍接受的分担比例。为了体现本方法的优越性,本文将以上三个方面所含方法同本文方法进行简单比较,得出下表,如表1所示。
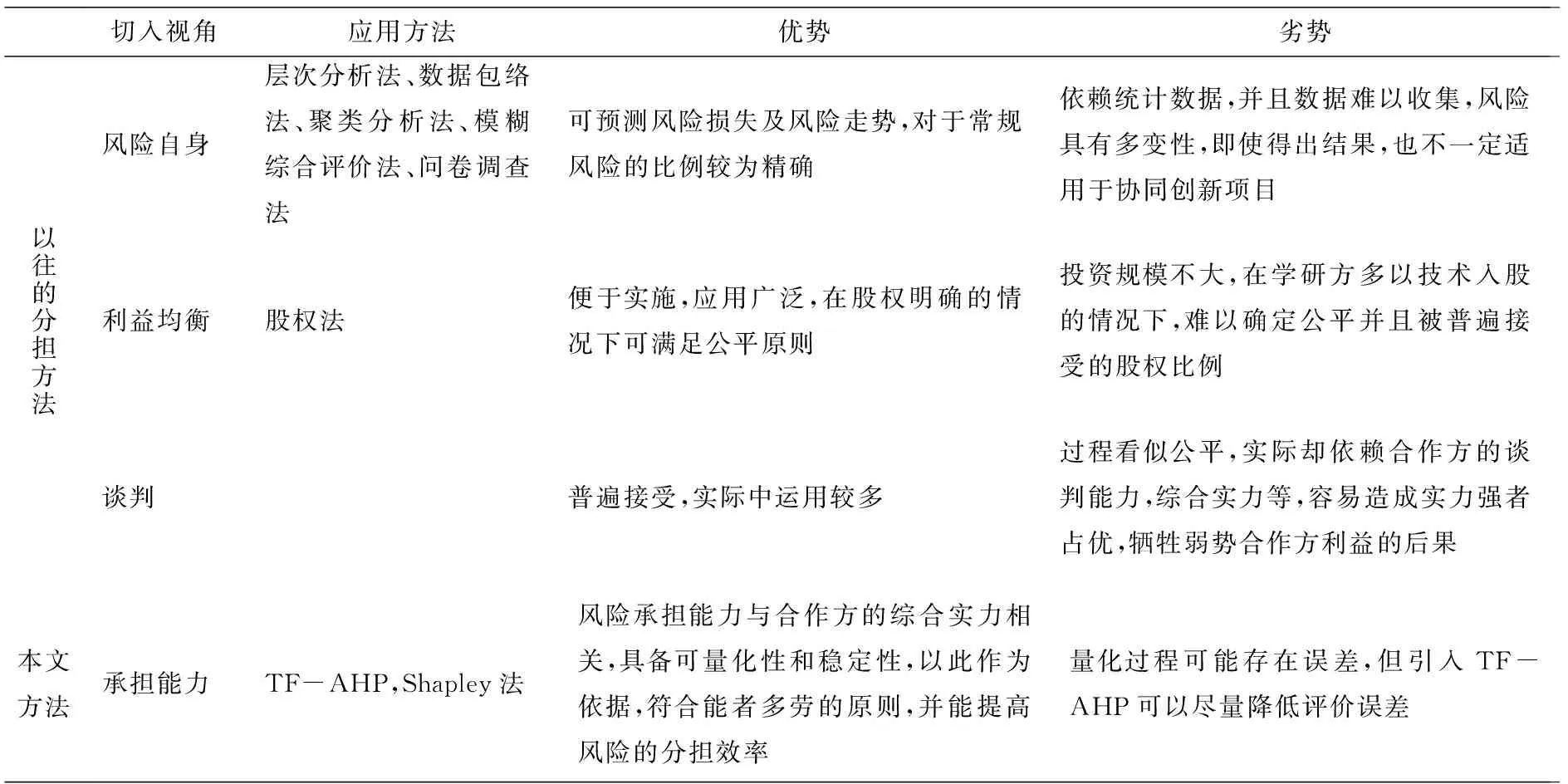
表1 协同创新分担方法优劣对比
三、风险分担模型构建
(一) s位专家给出各合作组合承担能力的模糊判断矩阵
请专家对各合作组合就某风险R1的承担能力进行评估,根据各合作组合对风险R1承担能力的相对强弱进行比较,标注方法如表2所示。
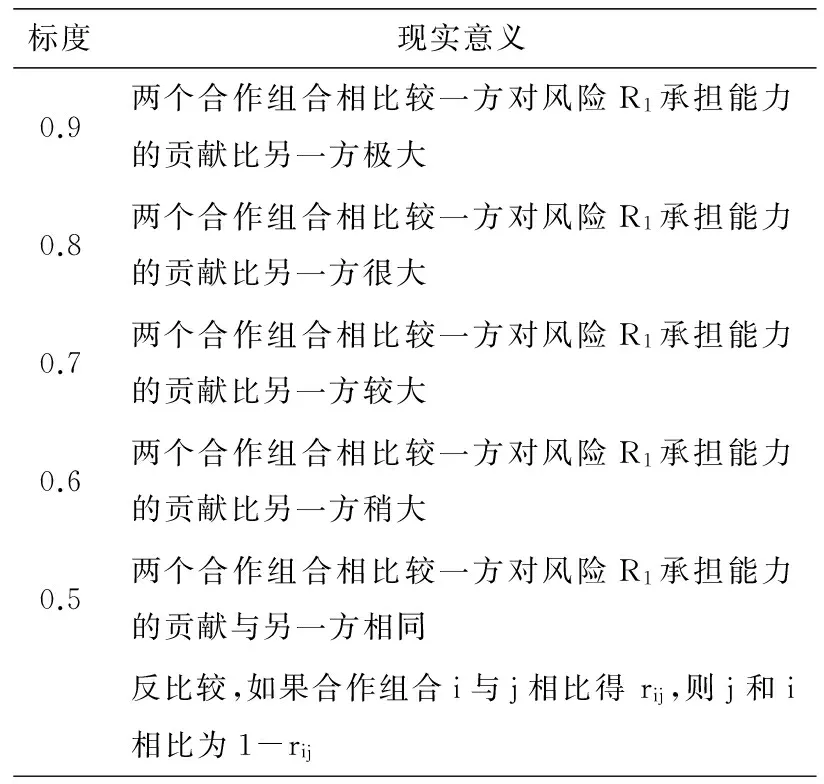
表2 风险承担能力比较标度方法
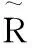
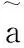
(二) 对所有专家给出的评分加权求平均值
根据参考文献[11]中的方法使用加权法将综合s位专家的偏好信息通过加权平均将模糊数整合成一个,其计算公式如下:
(1)
(三) 计算各合作组合对风险R1承担能力大小

(2)
(四) 去模糊化


(3)
对于任意一个模糊数,其大于另外其他k个模糊数的程度即任意合作组合对于风险R1的承担能力大于另外其他的合作组合的程度可以用式(4)表示:
(4)

(五) 通过Shapley值法确定各合作方对风险承担能力的贡献值,按比例得出风险R1的分担比例
通过三角模糊层次分析法可以得出每种合作组合对风险R1的承担能力v(xi)。利用Shapley值法计算各个协同创新合作方对风险R1的承担能力贡献值,以每个合作方加入协同创新项目对风险承担能力的贡献大小来合理地分担风险。则合作方对风险R1的承担能力贡献值可以由以下公式求得:
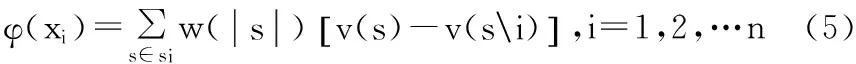
合作方i对风险R1的承担比例λi可以由下式求出:
(6)
四、算例
假设A、B、C三企业试图开展协同创新项目,由于项目是首次开展,没有先例可以作为参考,为防止经风险R1的发生,预计要投入100000元资金。如果这份损失三者平均分担,这种大锅饭式的分配势必会使风险承担能力较弱的合作方感到不公平,不利于合作的进行。此时即可采用前文提出的方法,使用TF-AHP先确定各个风险承担组合对风险R1的承担能力,然后利用Shapley值法确定每个合作方的风险承担比例。
假设5位专家根据表2对风险承担组合集{A,B,C,AB,AC,BC,ABC}给出的三角模糊数互补判断矩阵为:

①根据式(1)综合各专家的评价信息,详见附录2。
②根据式(2)计算得出各合作组合的模糊评价值为:
③根据式(3)、(4)去模糊化得:

经过上述步骤得到最终权重值即对风险R1承担能力量化值v(xA)=0,v(xB)=0.08,v(xC)=0.23,v(xAB)=0.53,v(xAC)=0.64,v(xBC)=0.71,v(xABC)=1
由此可以看出在协同创新中选择合作比单独承担时对风险的承担能力要强,相应地在面对风险时所获得效益也会增加。根据式(5)得到合作方A的对联盟风险承担能力的贡献值计算,如表3所示。将表中最后一行相加得到φ(A)=0.24。同理得φ(B)=0.315,φ(C)=0.445。
根据式(6)得出三者承担风险的比例分别为:24%,31.5%,44.5%,即A合作方需要投入24000元,B合作方需要投入31500元,C合作方需要投入44500元。

表3 合作方A风险承担贡献值计算表
五、结论
上述算例得出的结果表示在协同创新项目需要投入资金来预防风险时,合作方就此资金的分担比例。在面对较大的未知性时,依靠各合作方的风险承担能力来确定风险承担比例是一个切实可行的方法。本文依据各合作方对风险R1承担能力的强弱来确定其针对预防风险R1的风险投入资金比例,并在利益分配中根据此数据来调整最终结果。
本文方法的优点主要体现在以下三个方面:第一,客观性强。量化风险承担能力的过程严谨,降低主观判断的影响;第二,准确性强。风险承担能力与合作方自身的综合实力密切相关,相较于其他影响风险分担因素具有较强的稳定性,因此对于风险承担能力的量化准确性更强;第三,可行性强。操作过程简单,相比于以往方法对于历史数据的依赖性小。
协同创新的风险分担是一项必要且困难的工作,在大多数情况下,面对不确定的信息,合作方很难制定出能使参与各方都满意的风险分配比例。本文结合TF-AHP和Shapley值法,将合作方对风险的承担能力的大小作为分担风险的依据,为协同创新的风险分担提供了一种新思路,有效地降低了不确定性和主观因素的影响。
参考文献:
[1] Yeo K T, Tiong R L K. Positive Management of Differences for Risk Reduction in BOT Projects[J]. International Journal of Project Management, 2000, 18(4).
[2] Jin X H,Doloi H. Interpreting Risk Allocation Mechanism in Public-private Partnership Projects:An Empirical Study in a Transaction Cost Economics Perspective[J]. Construction Management and Economics, 2008, 26(7).
[3] Khazaeni G, Khanzadi M, Afshar A. Optimum Risk Allocation Model for Construction Contracts:Fuzzy Topsis Approach[J]. Canadian Journal of Civil Engineering, 2012, 39(7).
[4] Lam K C, Wang D, Lee P T K, et al. Modelling Risk Allocation Decision in Construction Contracts[J]. International Journal of Project Management, 2007, 25(5).
[5] Xu Y, Chan A P C, Yeung J F Y. Developing A Fuzzy Risk Allocation Model for PPP Projects in China[J]. Journal of Construction Engineering and Management, 2010, 136(8).
[6] 戴建华, 薛恒新. 基于Shapley值法的动态联盟伙伴企业利益分配策略[J]. 中国管理科学, 2004, 12(4).
[7] 李林, 贾佳仪, 杨葵. 基于合作博弈的协同创新项目的风险分担[J]. 社会科学家, 2015(3).
[8] 徐晓敏. 层次分析法的运用[J]. 统计与决策, 2008(1).
[9] 郭金玉, 张忠彬, 孙庆云. 层次分析法的研究与应用[J]. 中国安全科学学报, 2008, 18(5).
[10] 范如国.博弈论[M].武汉:武汉大学出版社, 2006.
[11] 姜艳萍, 樊治平. 一种三角模糊数互补判断矩阵的排序方法[J]. 系统工程与电子技术, 2002, 24(7).
[12] Chang D Y. Applications of the Extent Analysis Method on Fuzzy AHP[J]. European Journal of Operational Research, 1996, 95(3).
责任编辑:熊先兰
On the Research about Risk Sharing Method of Collaborative Innovation Project which Based on Risk Bearing Capacity
LI Lin,WANG Lu
(SchoolofBusiness,HunanUniversity,Changsha,Hunan410082,China)
Abstract:This paper puts forward ideas of using Triangular Fuzzy-Analysis Hierarchy Process(TF-AHP) to quantize the risk bearing capacity of each risk bearing combination of the selected risk,which is based on the contribution to the risk bearing capacity of each risk bearing partner calculated by Shapley Value Method to determine risk allocation proportion.
Keywords:collaborative innovation;risk bearing capacity;risk sharing; TF-AHP; shapley value method
收稿日期:2016-03-21
作者简介:李林(1963-),男,广西荔浦人,湖南大学工商管理学院教授、博士生导师,主要从事项目管理、绩效评价、创新管理等方面的研究。
基金项目:国家自然科学基金项目“协同创新项目利益多层次多阶段动态均衡及促进政策研究”(编号:71473076);国家自然科学基金项目“产学研协同知识创新生态系统演化机理与政策支持效应评价”(编号:71573078)阶段性成果。
中图分类号:F270
文献标识码:A
文章编号:1001-5981(2016)03-0014-05
