基于动态博弈模型的城市轨道交通定价方法

谭金会，何太碧，张倩文，张诗波

(西华大学汽车与交通学院，四川 成都　610039)



基于动态博弈模型的城市轨道交通定价方法

谭金会，何太碧，张倩文，张诗波

(西华大学汽车与交通学院，四川 成都610039)

摘要：城市轨道交通的票价是影响居民出行选择的重要因素，合理完善的轨道交通票价可以提高居民出行质量、优化客运结构、缓解城市交通压力。文章采用MNL模型描述不同公交方式的分担率，建立各公交方式的收益函数,引入动态博弈的方法构建轨道交通与常规公交的票价博弈模型，并求出相应的均衡解，最后以广东东莞市轨道交通票价的定价为例验证了模型的有效性。

关键词：城市轨道交通；定价；MNL模型；博弈论

制定合理的城市轨道交通票价，需要考虑企业的运营成本、运输市场需求、居民支付能力以及市场竞争状况等[1]，以达到既能吸引客流又能尽量减轻政府负担的目标。近年来，一些学者将现代经济学前沿工具融入到交通领域层面，取得了一些理论成果。Hollander等[2]深入探讨了博弈论在交通运输方向的运用情况，认为博弈论是分析交通运输系统功能强大的工具，分析了博弈状态下各交通运输模式之间的关系。Levinsonts[3]在微观基础上运用博弈论修正了拥堵定价理论，并认为拥堵定价可以作为一种合作机制以最大限度地减少总成本。仝允桓[4]构造了以票款收入最大为目标的最优票价模型及以充分发挥项目运能为前提的最优票价模型，并分别给出了补偿原则和补偿计算方法。贺国光等[5]研究了交通资源配置与交通方式选择的关系，考虑公交车和私家车两种出行方式，建立了双层博弈模型来讨论票价制定策略。黄园高等[6]运用博弈论方法研究了城市公共交通和收费公路在自由竞争和充分合作下的定价问题。目前，国内对博弈定价和公共交通的研究很多，但运用博弈理论研究轨道交通票价的仍较少。众所周知，客流运输的主体和核心是轨道交通和常规公交；因此，本文以轨道交通和常规公交为博弈对象，以票价为决策变量建立模型，分析东莞市公共交通现状及出行特点，并进行验证，以便为合理的票价制定提供建议。

1不同公交方式间的定价博弈分析

1.1乘客出行的交通方式选择模型

目前发展得较为成熟且在实际中应用较多的是Logit模型。本文采用多元MNL(the multinomial logit model)模型[7]表示不同交通方式的分担率，即：

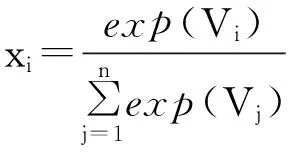
(1)

式中：xi为乘客选择第i种公交方式出行的概率；Vi表示第i种公交方式的效用函数。

1.2效用函数的确定

通常根据实际情况来选择具有代表性的影响因素建立模型。由于影响因素纷繁复杂，可将其划分为乘客的出行成本(包括时间成本、货币成本)和乘客感知(如安全性、便捷性、舒适性、可达性等)。将其统一换算为价值后采用的效用函数定义为

Vi=θ1Ti+θ2Pi+θ3εi。

(2)

式中：Ti、P、εi分别为第i种公交方式的时间成本、货币成本、感知成本，其中εi一般按5点量表法[8]进行量化处理；θ1、θ2、θ为影响乘客公交方式选择偏好的参数，可通过极大似然法[9]估计出θ1=0.28，θ2=0.53，θ3=0.37。

出行时间包括车外时间t1i和车内时间t2i，其中乘客的车外时间为

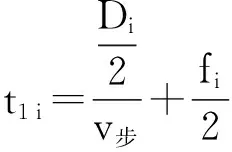
(3)

式中：Di为第i种公交方式平均站间距；v步为平均步行速度；fi为第i种公交方式平均发车间隔。

车内时间即行车时间，为

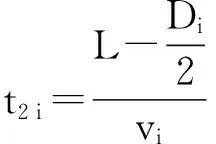
(4)

式中：L为居民平均出行距离；vi为第i种公交方式的平均速度。

故乘客出行的时间成本为

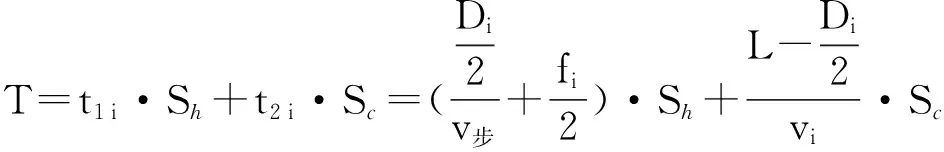
(5)

式中：Sh为候车及步行的时间价值；Sc为行车的时间价值。

将效用函数代入式(1)，则乘客选择第i种公交方式的概率，即第i种公交的分担率为

(6)

为了便于分析，令

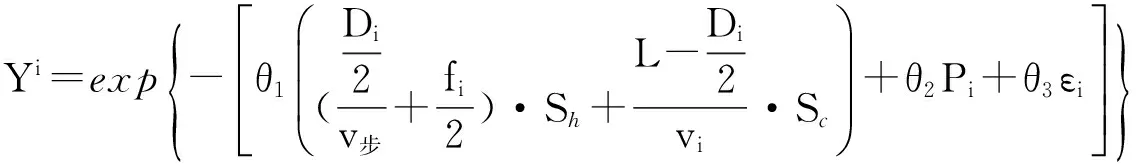
(7)

式中Yi只与第i种公交方式有关。Y-i表示除第i种公交方式外的向量，那么该模型可简化为

(8)

1.3不同公交方式的收益函数

假设某路段公共交通总客流为Q，则第i种公交方式所承担的客流量qi为

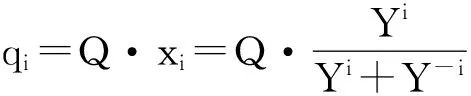
(9)

那么第i种公交方式的收益函数为

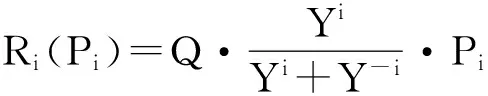
(10)

式中Pi为第i种公交方式的票价。

2博弈模型的建立

自身收益最大化是不同运营方竞争博弈的关键[10]，但票价又受到政府的管制，只能在政府限定的价格上下限浮动。用非线性规划模型表示为

maxRi(Pi,P-i)，

(11)

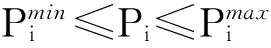
(12)

式中：Pi为第i种公交方式的价格策略；P-i表示除第i种公交方式外的公交方式价格策略。

在上述博弈中，当存在一种票价策略P*，使得不同公交方式的收益函数均达到最大，则该点即为博弈模型的均衡解。此博弈均衡解[11]可表述为

(13)

结合式(7)和(9)，可得票价

(14)

故这2种公交方式的收益函数为：

R1=q1·

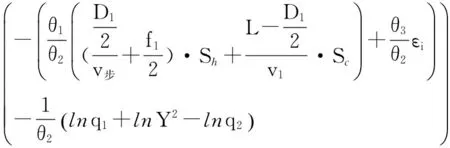
R2=q2·

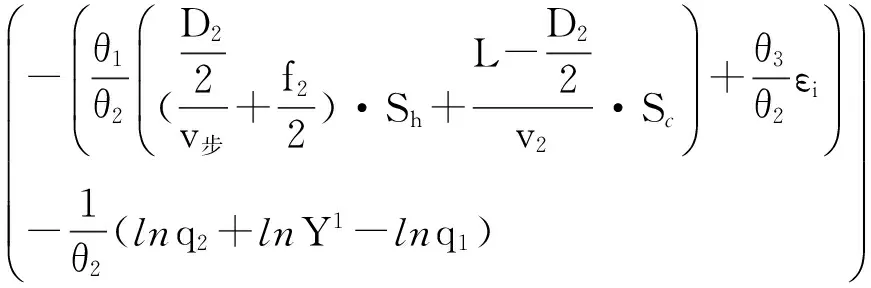
(15)则这2种公交方式定价策略的均衡状态可表示为：

(16)

该模型可以利用剔除严格劣战略法来得到定价博弈模型的均衡解。

3实证分析

3.1东莞市公共交通现状及出行特点

随着东莞城市空间的扩大、居民出行观念的转变以及珠三角地区联系的不断紧密，人们对交通网络功能和出行质量的要求日益提高。城市快速轨道交通的建设无疑为居民出行提供一种快速便捷的交通方式，提高乘客出行舒适度，从而提高居民的出行质量。未来东莞将形成“四大专业中心区”，并通过轨道交通的建设紧密连接在一起，为行政区划调整、生态安全系统的优化、环境质量的改善创造条件。

东莞市居民出行调查显示，居民出行方式主要是摩托车出行，占机动车出行的59%，是东莞市居民乘车出行中的第一出行方式；但目前，东莞市已经开始实施对摩托车的限制发展策略，在这一策略下，摩托车这种在东莞最为普遍的个体交通方式将会受到制约，进而影响到人们日常出行，因此，发展快速轨道交通能为人们出行提供一个高效、环保的选择模式，将有力支撑城市交通发展战略的实现。

3.2地铁2号线票价定价分析

以东莞地铁2号线一期工程(全长37.8 km)和常规公交118路运行情况为例。地铁2号线和118路按照相关规定均实行分段收费制。令“陈屋—虎门火车站”路段为L，建立东莞地铁2号线与常规公交118路的定价博弈模型，并求出均衡解。

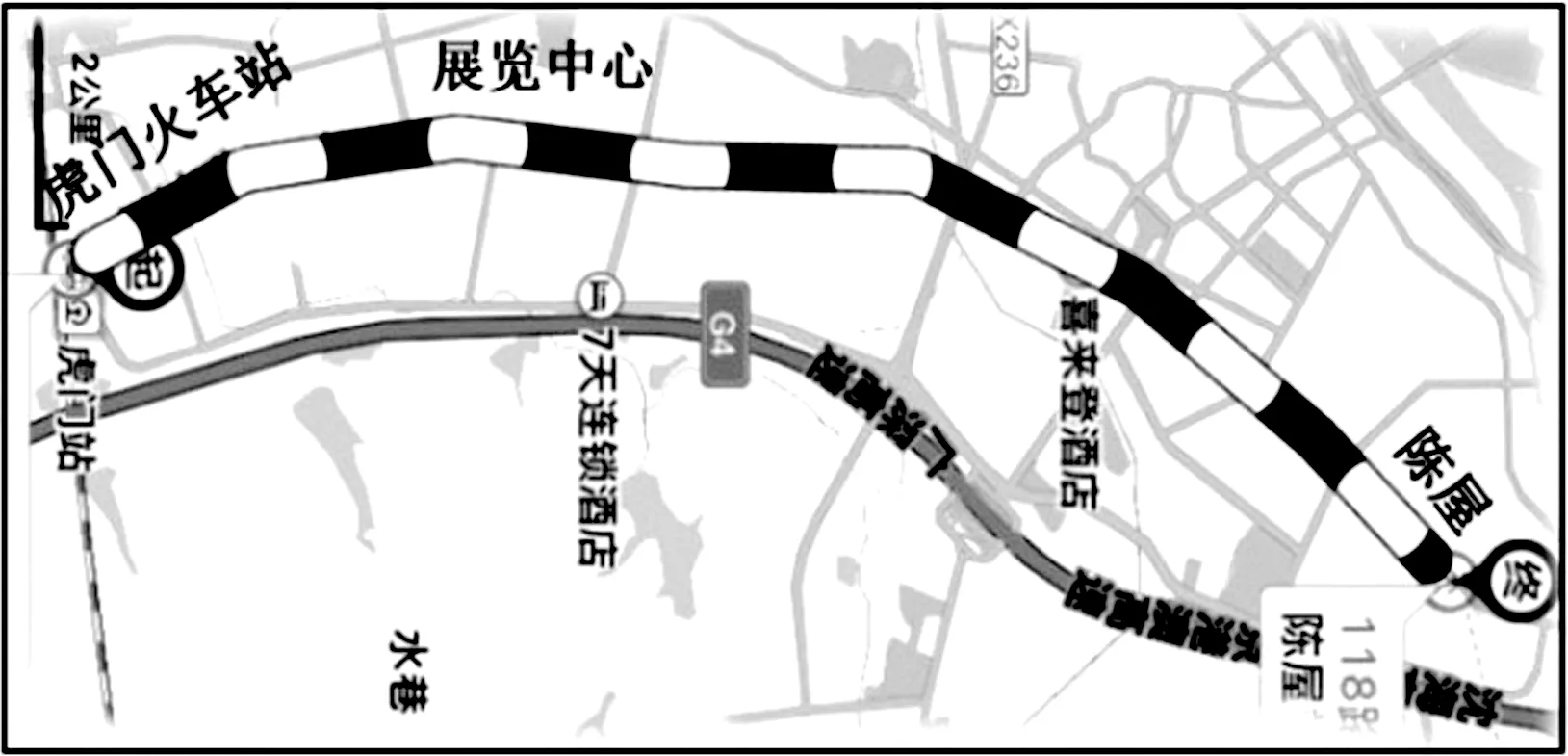
图1　东莞市公交118路运行路线

注：地铁2号线尚未开通，2016年5月正式开通运行。

假定地铁票价2元起步，可乘坐4 km；超过4 km的，每递增4 km增加1元；12 km以外，按越远越实惠原则每递增6 km增加1元。根据相关资料[12]，获取相关数据如表1所示。

表1　地铁与常规公交特性参数

注：本文公交平均运行速度取20 km/h；地铁平均运行速度取40 km/h；v步取4 km/h。

据统计数据[13]显示，2014年东莞市在岗职工平均工资为3万6 057元/年，即3 005元/月，则目前该市出行者收入约为17元/h。参考相关研究[14]，对交通成本进行量化，计算得出候车和步行的时间价值Sh=0.425元/min，行车的时间价值Sc=0.14元/min。

据相关研究[12]，假定给定参数1≤p1≤6，1≤p2≤4，计算出2种公交方式在路段L上的均衡票价如表2所示。

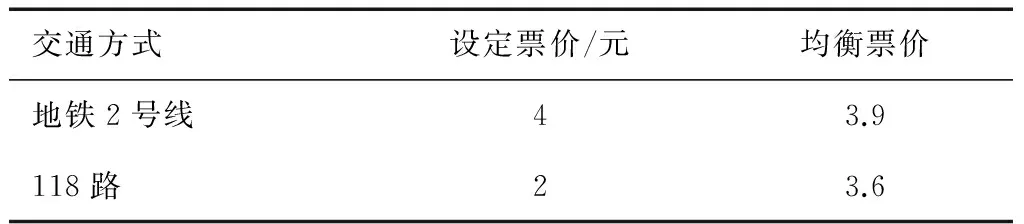
表2　地铁2号线与公交118的均衡票价

从表2可以看出，地铁2号线在陈屋到虎门火车站的均衡票价比设定票价略低，而118路在该路段的均衡票价比设定票价高出较多，四舍五入得到地铁和公交的均衡票价均应为4元。由此票价差价可简单得出若使用以上均衡票价后，地铁的运营收入不变，公交的运营收入将会翻倍，此票价即为此段的最优票价。这与2015年8月召开的“东莞市城市轨道交通票价听证会”所确定的票价方案基本相符。

3.3客流敏感性分析

轨道交通的价格因素包括轨道交通自身票价的绝对价格和与常规公共交通相比较的相对价格，两者都会影响居民对出行方式的选择。假定常规公交线路的票价按照模型中标定的数值不变，结合调研数据和Transcad软件对轨道交通在各主要特征年进行预测，票价增减对客流影响的敏感性分析如表3所示。

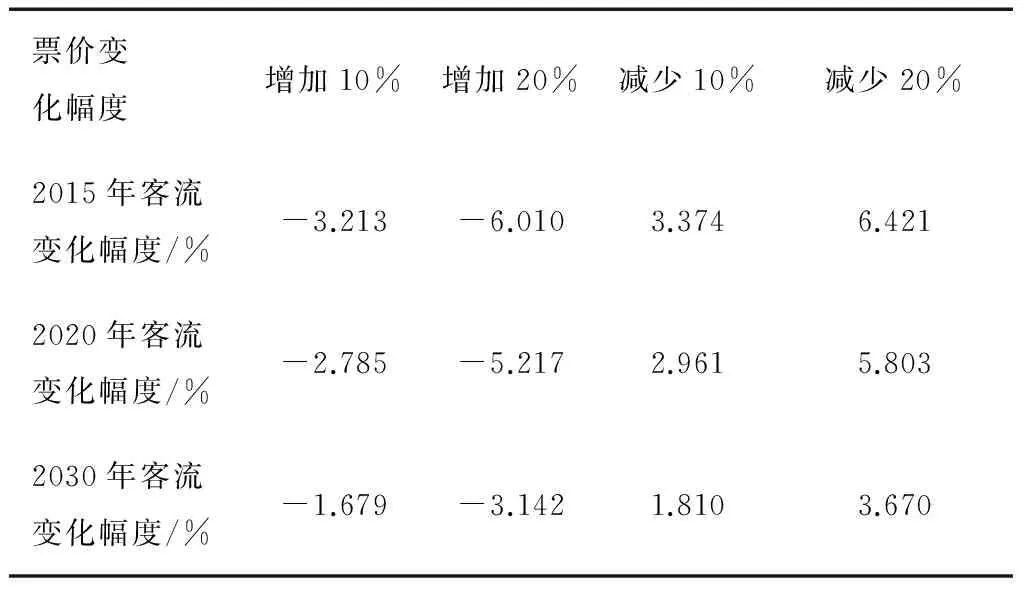
表3　票价水平与客流敏感性分析

可以看出，轨道线路运营的初期票价水平对客流的影响较大，随着今后线网的不断优化和完善，票价对客流的影响逐渐降低，票价敏感性也越来越小。这说明轨道线路运营的初、近期不宜轻易调高票价，否则轨道交通对居民的吸引力将打折扣。

由于东莞市城市特点的不同，城市结构松散且外来务工人员较多。与市内常住居民相比，外来务工人员对于票价更为敏感。2015年5月笔者对东莞市外来务工人员进行轨道交通票价意愿调查，调查显示：对大于10 km的轨道交通票价有近90%认为应低于5元，认为应小于等于3元的占到51.6%；对于10 km以内的轨道交通愿意接受3元及以下票价的占到93%，其中认为2元的占到了70%，普遍希望票价不要定得太高。

4结束语

城市轨道交通票价的制定是一个复杂的动态过程。本文以票价作为决策变量建立不同公交方式的动态博弈模型，对其简化求解，最后用某市公共交通的实例对模型进行了验证，并就票价增减对客流的影响进行了预测。实例证明了该方法得出的票价与东莞市轨道交通票价听证会的结果基本吻合。本文只做了地铁与公交两方博弈的实例，还有待对三方甚至更多公交方式参与的情况进行更为深入的模型验证分析，同时也需要考虑合作联盟下多方利益的分配，这些都有待进一步的研究。

参考文献

[1]王俊龙.城市轨道交通票价定价策略及模型研究[D].兰州:兰州大学,2014.

[2]Hollander Y, Prashker J N. The Applicability of Non-cooperative Game Theory in Transport Analysis[J].Transportation，2006,33:481.

[3]Levinson D. Micro-foundations of Congestion and Pricing: A Game Theory Perspective[J].Transportation Research Part A,2005,39:691.

[4]仝允恒.城市快速交通线项目的最优票价与政府补偿[J].系统工程理论与实践,2001(4):88.

[5]贺国光,刘峰涛.基于双层博弈模型的交通方式的选择[J].长安大学学报(社会科学版)，20068(3):4.

[6]黄园高,周晶.收费公路和公共交通之间的定价博弈分析[J].东南大学学报(自然科学版),2004,34(2):268.

[7]聂伟.都市圈道路网络优化及其平价理论研究[D].北京:北京交通大学,2007:72.

[8]刘洪营.城市客运交通结构评价设计与优化研究[D].西安:长安大学,2003.

[9]王镜.基于博弈分析的城市公共交通定价及补贴的理论方法研究[D].北京：北京交通大学,2008.

[10]Yaron Hollander, Joseph N Prashker. The Applicability of Non-cooperative Game Theory in Transport Analysis[J].Transportation,2006,33:481.

[11]Harker P T. Generalized Nash Games and Quasi-variational ineuqualities[J]. European Journal of Operational Research,1991,54:81.

[12]过秀成,李家斌.轨道交通运营初期公共交通系统优化法[M].南京：东南大学出版社,2015:17-18.

[13]中华人民共和国国家统计局.《中国统计年鉴2014》[M]. 北京：中国统计出版社,2009:113-117.

[14]王玉萍.常规公交与轨道交通之间的竞争与合作[D].西安：长安大学,2004:23-25.

(编校：夏书林)

Research on the Pricing Method of Urban Rail Transit based on Dynamic Game Model

TAN Jinhui, HE Taibi, ZHANG Qianwen, ZHANG Shibo

(SchoolofAutomobileandTraffic,XihuaUniversity,Chengdu610039China)

Abstract:Urban Rail Transit fare is an important factor affecting residents travel choice. The reasonable improvement of the rail transport fares can improve the residents' travel quality, optimize the structure of passenger transport and ease urban traffic pressure. The MNL model was used to describe the different traffic patterns and establish the revenue function of each mode of public transport. a dynamic game method was adopted to build rail transit and bus fare Game Model and work out the corresponding equilibrium. Finally, the validity of the model is verified with a numerical example of rail transit ticket price of Dongguan City Guangdong Province .

Keywords:urban rail transportation; pricing; MNL model; game theory

收稿日期：2015-10-21

基金项目：西华大学汽车测控与安全四川省重点实验室开放课题资助(szjj2015-044); 西华大学研究生创新基金(Ycjj2014153)。

中图分类号：F505

文献标志码：A

文章编号：1673-159X(2016)03-0036-4

doi:10.3969/j.issn.1673-159X.2016.03.008

第一作者：谭金会(1970—)，女，副教授，主要研究方向为车辆工程及道路交通安全。

·新能源汽车与低碳运输·