基于改进RM界的二次损失函数支持向量机模式选择

杨晓欢，王晓明，田　勇，宋景平

(1. 西华大学理学院，四川 成都　610039；2. 西华大学计算机与软件工程学院，四川 成都　610039；3. 西藏飞跃智能科技有限公司，西藏 拉萨850000)



基于改进RM界的二次损失函数支持向量机模式选择

杨晓欢1，王晓明2*，田勇2，宋景平3

(1. 西华大学理学院，四川 成都610039；2. 西华大学计算机与软件工程学院，四川 成都610039；3. 西藏飞跃智能科技有限公司，西藏 拉萨850000)

摘要：半径-间隔界中最小包含球半径R的计算需要求解二次规划问题，增加了算法的计算量。为提高计算效率，提出一种基于改进RM界的二次损失函数支持向量机模式选择。用所有训练样本的最大距离D逼近半径R，用D替换R构成新的RM界，然后基于改进的RM界对二次损失函数支持向量机(L2-SVM)进行模式选择，并用梯度下降法调节最优参数。对算法的分类精度和计算效率进行仿真实验讨论，结果表明，与基于RM界的模式选择相比，虽然该算法的分类精度没有明显改变，但其计算效率至少提高1倍。

关键词：模式选择; 支持向量机; 半径-间隔界; 梯度下降法; 半径-间隔界

基于统计学习理论的支持向量机(support vector machine，SVM)是20世纪90年代Vapnik等提出的一种新的学习方法[1]，用于探索有限样本情况下机器学习的规律。支持向量机区别于其他统计学习算法的显著特点是根据结构风险最小化准则，通过最大化分类间隔构造最优分类超平面，从而提高分类训练器的泛化能力。它有效克服了样本维数高、非线性、过学习等弊端，在模式识别、特征提取、回归估计等领域得到广泛应用[2-5]。

核方法的引入[6]，使支持向量机的学习从线性空间扩展到非线性空间，同时也增加了算法的参数。支持向量机优化问题中的二次规划参数选择、核参数选择统称为模式选择，它对支持向量机的性能有着重要影响，已成为研究的热点之一[7-9]。常见的参数选择方法有k-重交叉验证(k-fold cross-validation)[10]和留一法(Leave-one-out，LOO)[11]，其本质是参数空间穷尽搜索法；但是穷尽搜索法计算量较大，难于实现。有效的方法是通过计算结构风险上界的某种估计来选择参数。O.Chapelle等[12]基于最小化风险上界的标准，提出支持向量机留一法误差上界的方法。它是分类器真实错误率的一个无偏估计，寻优效果准确，但是与文献[13]介绍的半径-间隔界(radius-margin bound,RM)方法相比，仍然需要较大的计算量。目前，RM界是普遍用于模式选择的一种风险估计上界，能取得较好的结果。文献[13]通过考虑样本在特征空间的分布结构和最优分类面的权向量，构造了连续的、容易计算的RM界；但针对非线性情况，基于RM界训练的算法性能不稳定，需要通过变换核函数，将其由软间隔转变为硬间隔，最终利用基于RM界的SVM来优化其参数。

梯度的迭代优化算法[14]经常用于求解基于界的参数寻优问题。这类算法不仅可以自动调节参数，而且减少了计算量，适合于多参数的选择问题；但是当基于应用广泛的RM界时，每次迭代都需要求解2次二次规划问题，即最优分类面的权向量和训练样本的最小包含球半径，增加了分类器的训练计算量。

Huyen等[15]在寻找最大分类间隔时，对支持向量数据描述(support vector data description, SVDD)[16]中的最小包含球半径进行了深入研究，通过理论证明，得到了最小包含球半径的近似估计。针对基于RM界的梯度下降法调节最优参数，会严重影响计算效率的问题，本文首先用所有训练样本的最大距离D近似估计半径R，从而避免求解二次规划问题带来的较大计算开销，然后用D替换R构造新的RM界，来估计支持向量机的最小风险上界，最后基于改进的RM界，对二次损失函数支持向量机进行模式选择，并用梯度下降法调节最优参数，以达到减小计算开销并提高SVM性能的效果。为能高效的调节最优参数，提高支持向量机的分类性能和泛化能力，笔者的工作将集中于惩罚系数C和高斯核参数σ的选择。

1二次损失函数支持向量机及其模式选择

1.1二次损失函数支持向量机

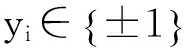
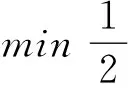
s.t.yi(w·φ(xi)+b)≥1-ξi,i=1,2,…,l。

(1)

式中：w为分类超平面的权矢量；C为惩罚系数，控制着错分样本的惩罚程度；ξi为松弛变量；φ(x)为输入空间到特征空间的一种非线性映射；b为最优超平面的偏量。

应用Lagrange乘子法和KKT条件求解上述优化问题，即

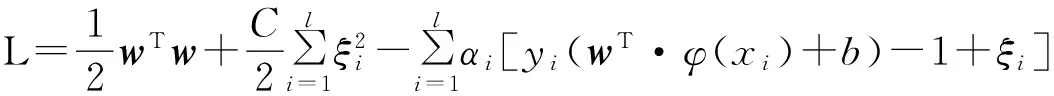
(2)

其中αi为Lagrange乘子，且αi≥0，由此得到：

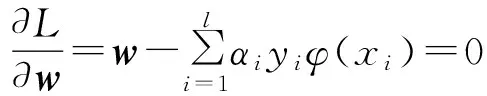
(3)

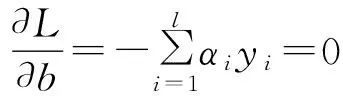
(4)

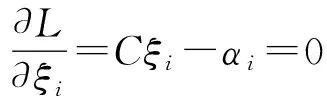
(5)

将式(3)—(5)代入式(2)，可以得到Wolfe对偶问题，为：

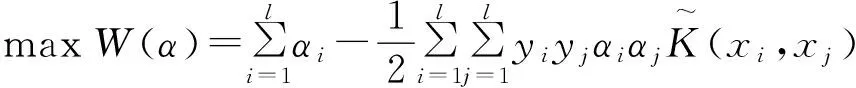
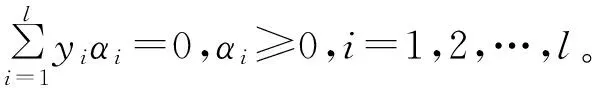
(6)

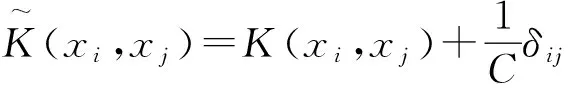
通过核函数把样本空间映射到高维特征空间，采用应用最广泛的RBF核，即

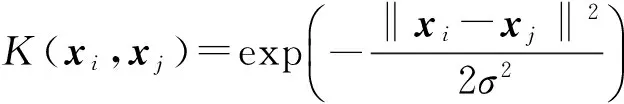
(7)

1.2RM界(radius-margin bound)

LOO估计是分类器真实错误率的一个无偏估计；但由于LOO估计计算量大，无法有效应用于实际中。Duan等[13]提出一种针对硬间隔支持向量机结构风险的RM界，解决了计算量大的问题。RM界定义为

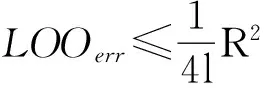
(8)

式中：LOOerr为SVM的结构风险误差估计；R为SVDD的最小包含球半径；w为最优分类面的权向量。

RM界表明SVM的结构风险由样本在特征空间的分布形状和最优分类面的权向量这2个因素决定。w可由式(6)求得，即‖w‖2=2W(α)。R可由下面的二次规划问题求得：

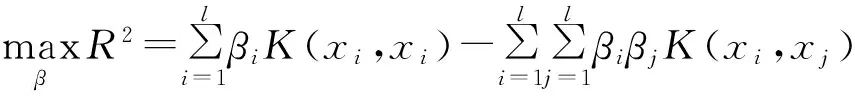
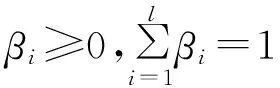
(9)

由式(6)和式(9)可知，当用梯度下降法自动选择最优参数时，每次迭代过程都需要求解2次二次规划问题，这无疑是一个较大的计算开销。为此，试图对最小包含球半径R的上界做出近似估计，避免求解二次规划问题，从而减小计算量。

2基于改进RM界的二次损失函数模式选择

2.1最小包含球半径R的近似估计

RM界是应用较广泛的一种风险上界，但RM界的估计需要求解2次二次规划问题，降低了计算效率。Huye等[15]通过理论证明，提出了一个容易计算的最小包含球半径的上界估计，即用所有训练样本间的最大距离近似的逼近半径R。显然，相比于通过二次规划问题求解半径R，寻找样本间的最大距离这一方法更易实现，而且显著减少了参数选择的计算开销。半径的上界估计为

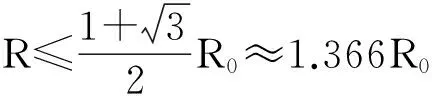
(10)

式中，R0=D/2，D表示所有训练样本间的最大距离。

由式(10)可知，D是R上界的估计。显然，D的估计易于R的估计，不仅避免每次迭代中求解二次规划问题，而且D的估计是稳定的，仅随参数的变化而变化。基于此，用D2替换R2，得到一个新的支持向量机期望风险上界，从而高效地调节最优参数，达到缩减计算开销且提高分类性能的效果。

2.2基于改进RM界的模式选择

支持向量机通过模式选择得到算法最优参数，同时满足结构风险最小的准则。对于数目有限的训练样本，无法准确地计算结构风险，为此，可行的方法是应用某种估计逼近风险上界，并根据这种估计进行模式选择。LOO估计的计算量大，无法有效应用于实际中。RM界是目前应用较广泛的一种误差界，是连续的且容易计算的一种风险上界；但RM界的估计需要求解2次二次规划问题，在梯度下降法的迭代中明显降低了计算效率。为此，笔者改进RM界，用样本间的最大距离近似地估计最小包含球半径，得到改进的RM界，为

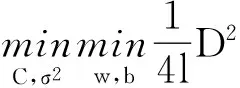
(11)

式中，D表示所以训练样本间的最大距离，D2由式(12)计算得到

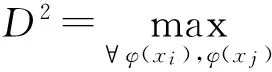
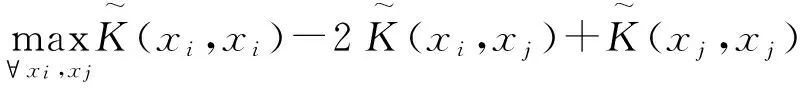
(12)

‖w‖2通过式(6)的二次规划问题求解，C和σ2为要调节的超平面参数。此时，新的RM界的估计函数可以表示为

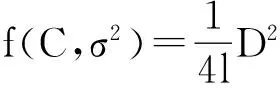
(13)

所以问题的关键变成如何计算D2和‖w‖2相对于参数(C,σ2)的梯度，相关的梯度计算为：

(14)

式中，‖w‖2的偏导数计算为：

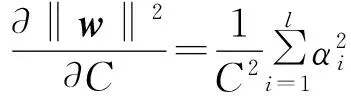
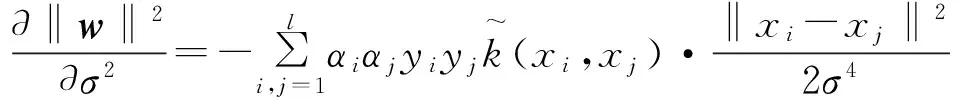
(15)

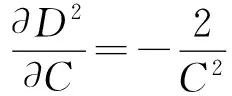
(16)

把式(15)(16)代入式(14)中，即可求得f关于参数C和σ2的梯度。基于改进的RM界，用梯度下降法寻找L2-SVM的最优参数步骤如图1所示。

输入:训练样本集X,参数初始值C0,σ20,步长η,迭代终止误差ε。输出:最优参数C*,σ*。步骤1:根据已知参数,由式(6)求解二次规划问题,即‖w‖2=2w(α),由式(12)计算最优值D2,并由式(13)计算f,得到f0。步骤2:由式(14)—(16)计算f梯度值,即f(C,σ2)CC=C0,f(C,σ2)σ2σ2=σ02。步骤3:用步骤2中计算得到的梯度值更新参数C,σ2,即C=C0+ηfC,σ2=σ20+ηfσ2。步骤4:由式(13)更新f,并判断|f-f0|≤ε是否成立,若成立,则终止迭代,输出最终参数C*,σ*;否,则返回步骤2继续求解。

图1梯度下降法寻找L2-SVM的最优参数步骤

由上述算法步骤获得最优的参数C*，σ*，就可计算L2-SVM的决策函数，为

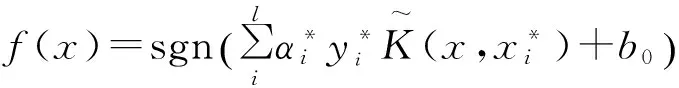
(17)

式中，最优超平面的偏量b0由式(18)计算而得

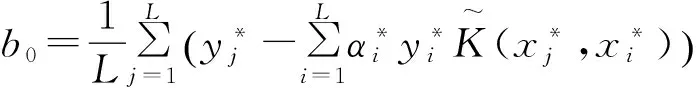
(18)

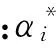
2.3算法分析

所有样本的最小包含球半径和样本间的最大距离都是对样本在特征空间中的分布形状的描述。由式(10)可知，D是R上界的估计，是对R估计的一个逼近，所以改进的RM界，即D2‖w‖2与传统RM界R2‖w‖2存在一定的关联。为探索两者之间的关系，通过实验对其分析。

首先，从UCI真实数据集中选择Heart为实验数据，然后在给定的初始值下计算D2‖w‖2和R2‖w‖2的值。为实验效果明显，在相同的条件下，先固定参数σ的值，随机选取不同的参数C的值计算D2‖w‖2和R2‖w‖2，其结果如图2 (a)；反之，固定参数C的值，随机选取不同的参数σ，计算D2‖w‖2和R2‖w‖2，其结果如图2(b)。可知，D2‖w‖2与R2‖w‖2在相同的参数取值条件下，有相近的关联关系，即两者的变化趋势相同，计算值相近，差异较小；所以D2‖w‖2是R2‖w‖2的近似估计，在参数寻优过程中，可用D2‖w‖2代替R2‖w‖2参与二次损失函数支持向量机的参数调节。

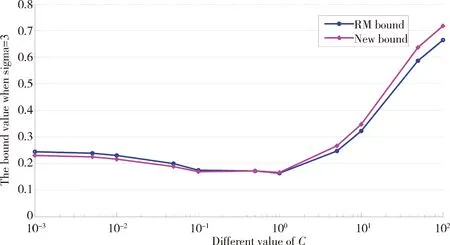
(a)σ=3

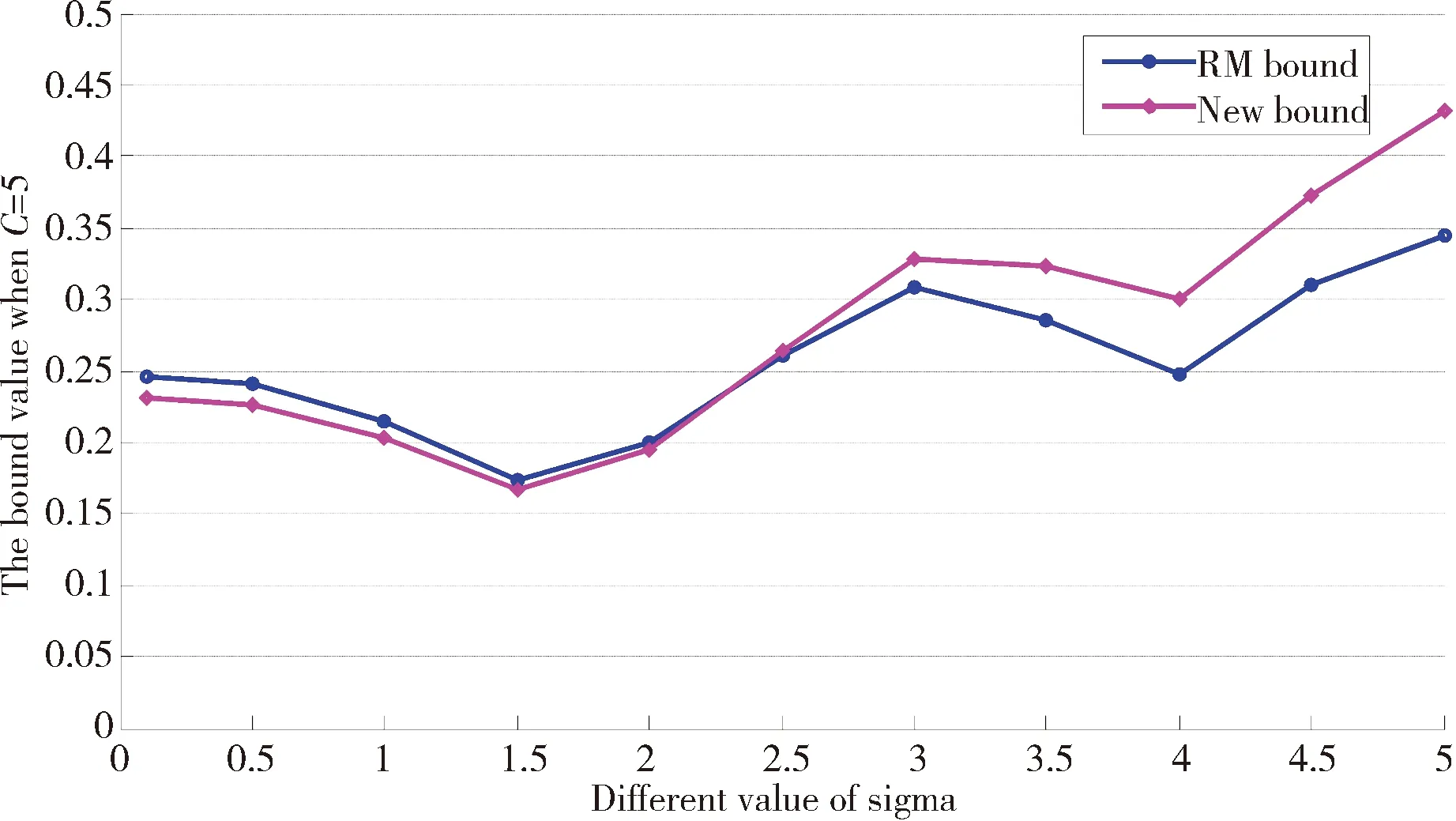
(b) C=5

3实验结果与分析

为验证改进算法的有效性，对算法的分类精度和计算效率进行实验研究。实验分为2部分：1)通过实验计算K-近邻算法(KNN)、一次损失函数支持向量机(L1-SVM)、基于RM界进行模式选择的L2-SVM，以及文中改进的算法的分类精度，比较4种分类算法基于不同训练样本的识别率；2)研究基于传统RM界进行模式选择的L2-SVM和文中改进算法的运行时间，比较算法的计算效率。采用内存为2GB，操作系统为64位window7的个人计算机，所有算法采用MATLAB2010b编程实现。

3.1分类精度比较

为比较算法的分类效果，使用UCI真实数据集进行实验，实验数据来自http://www.ics.uci.edu/～mlearn/MLRepository.html。从中选取6个数据集，数据集相关信息已在表1中给出。实验时，设定KNN算法中的近邻数K=5。L1-SVM中的参数C和σ，采用5重交叉测试对其选取。对于L2-SVM，一方面基于RM界进行模式选择，另一方面采用文中改进的RM界选择参数。因为梯度下降法的步长不是文中研究的重点，所以固定其为0.05。为满足约束条件C>0，σ>0，令u=lnC，v=lnσ2。先对数据进行归一化处理。对于每一个数据集，分别选取{10%，20%，30%，40%，50%，60%，70%，80%}为训练数据，剩余的为测试数据。分别计算4个算法基于各个训练样本集的分类正确率，其实验结果如图3所示。

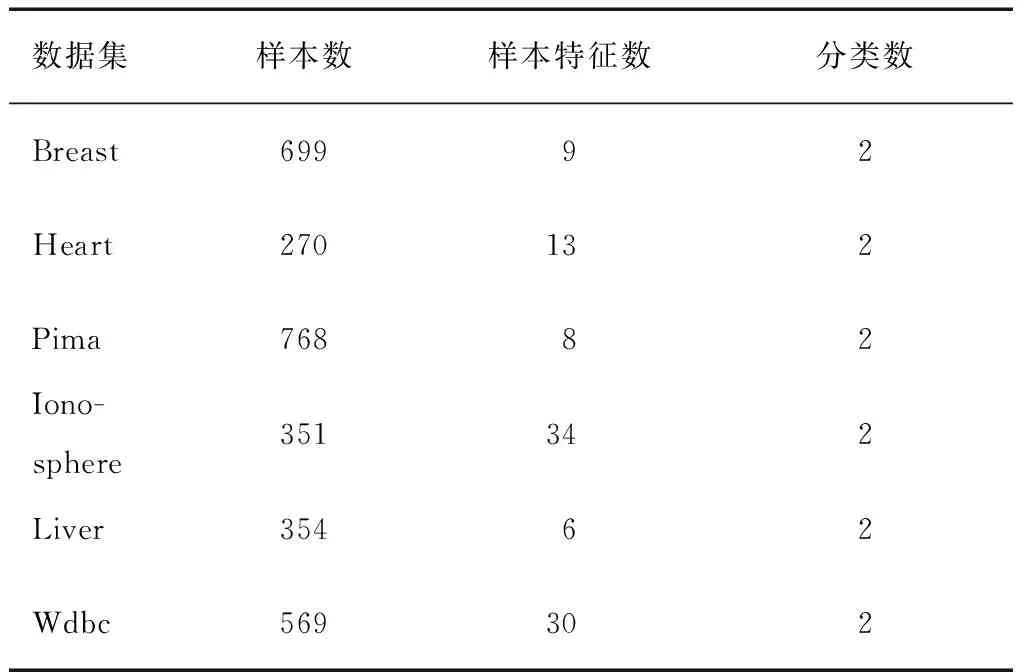
表1　UCI数据集特征

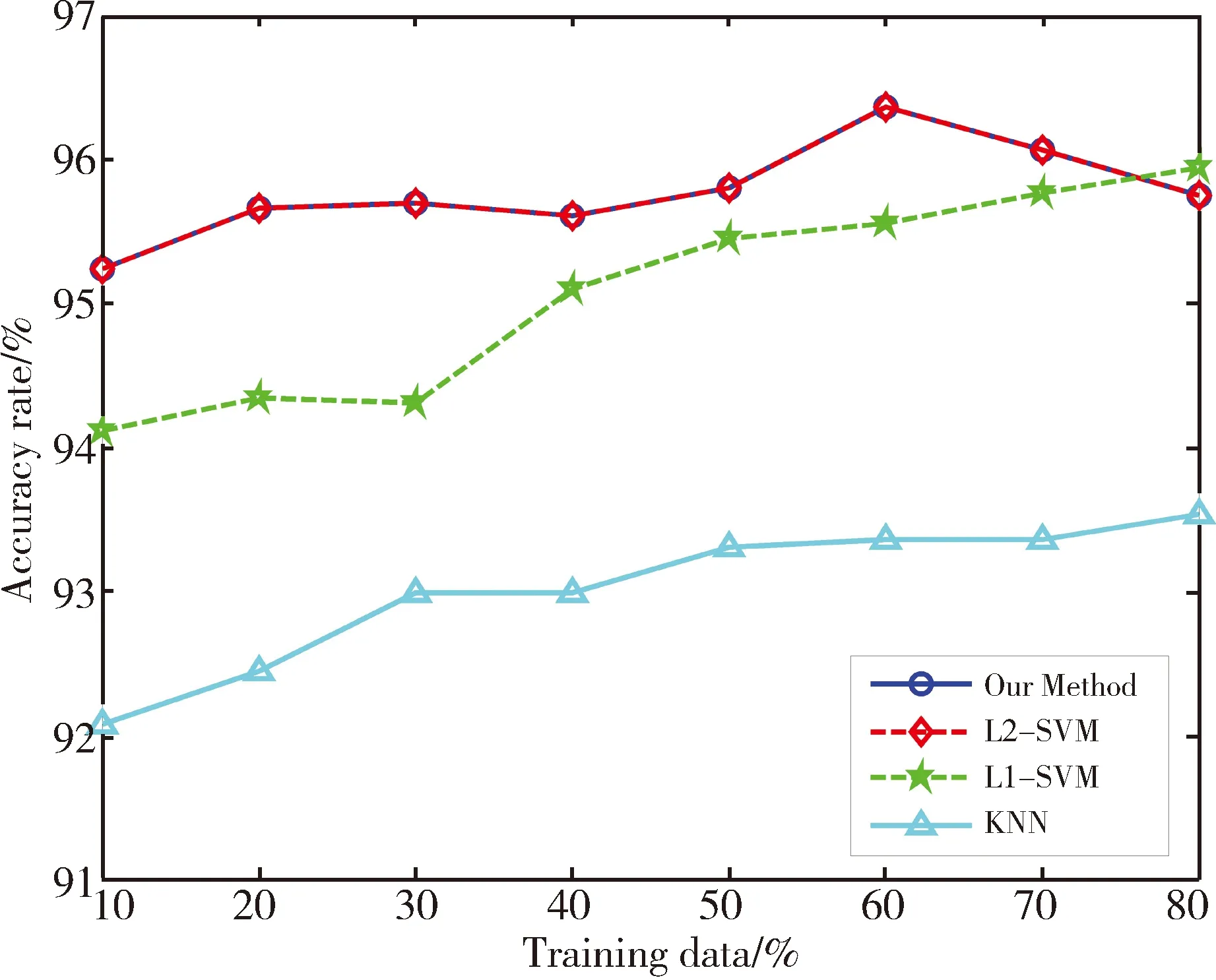
(a)Breast

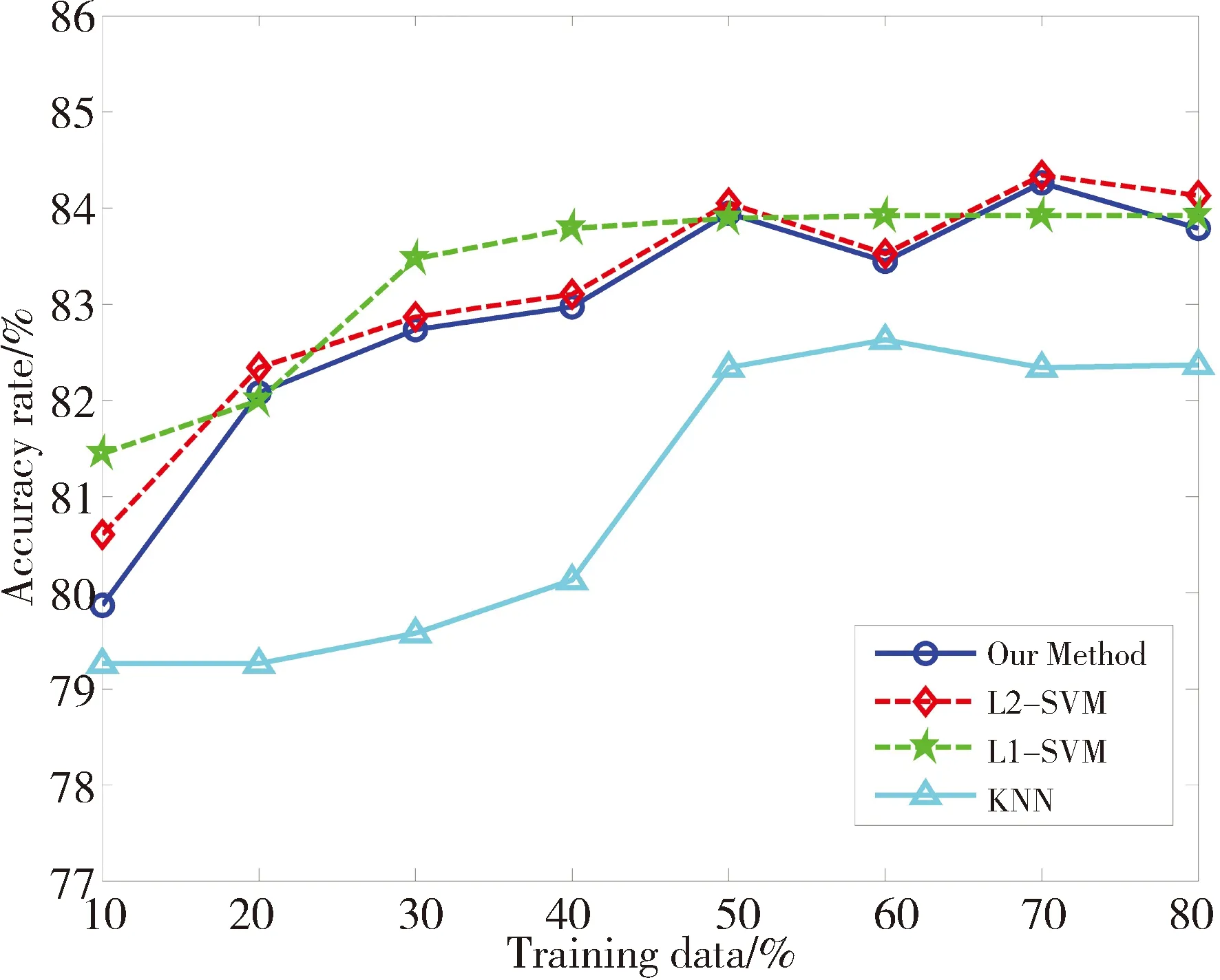
(b)Heart

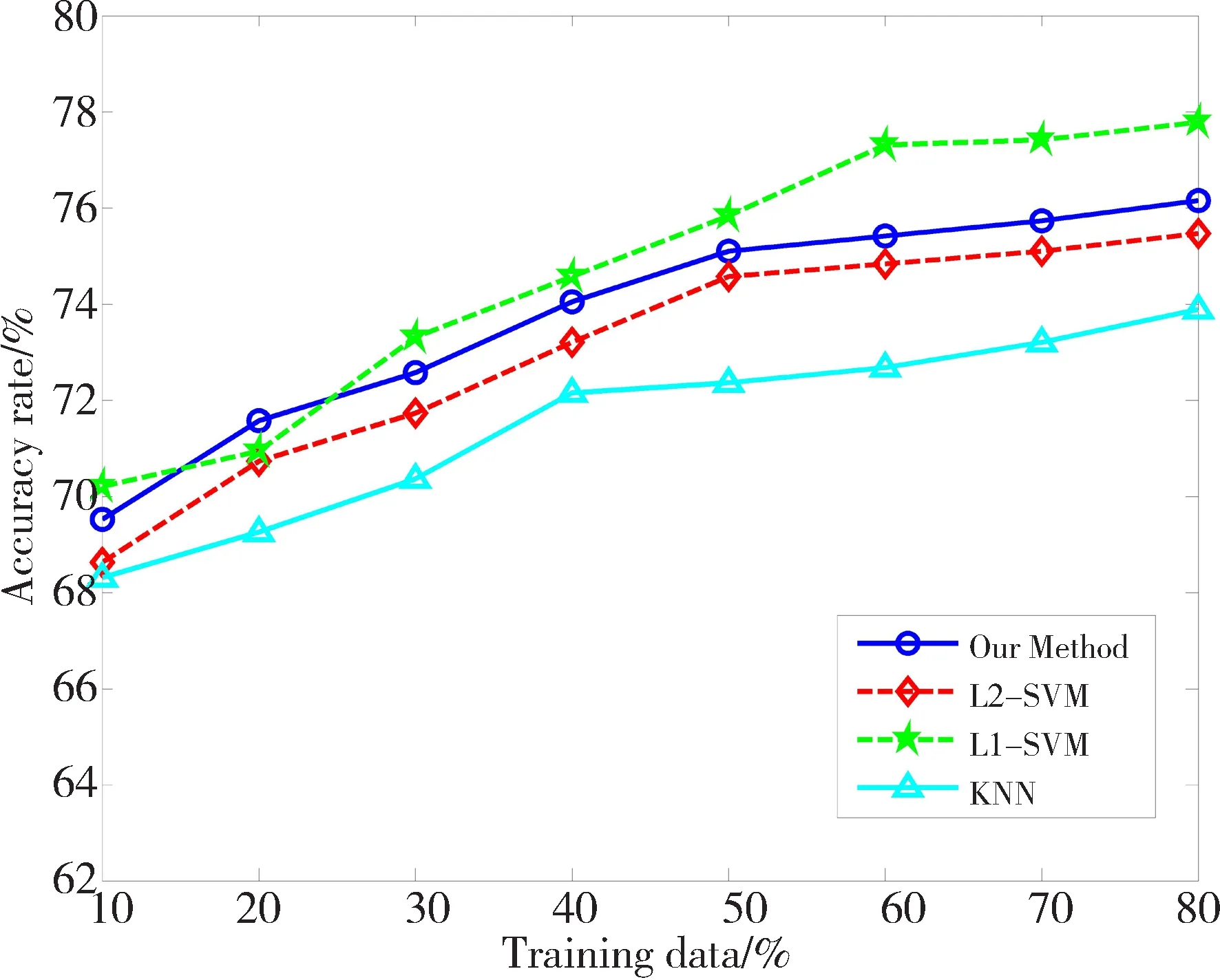
(c)Pima

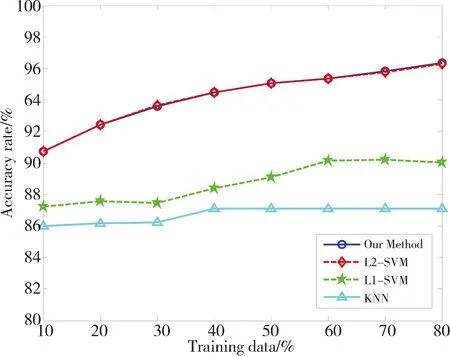
(d)Ionosphere

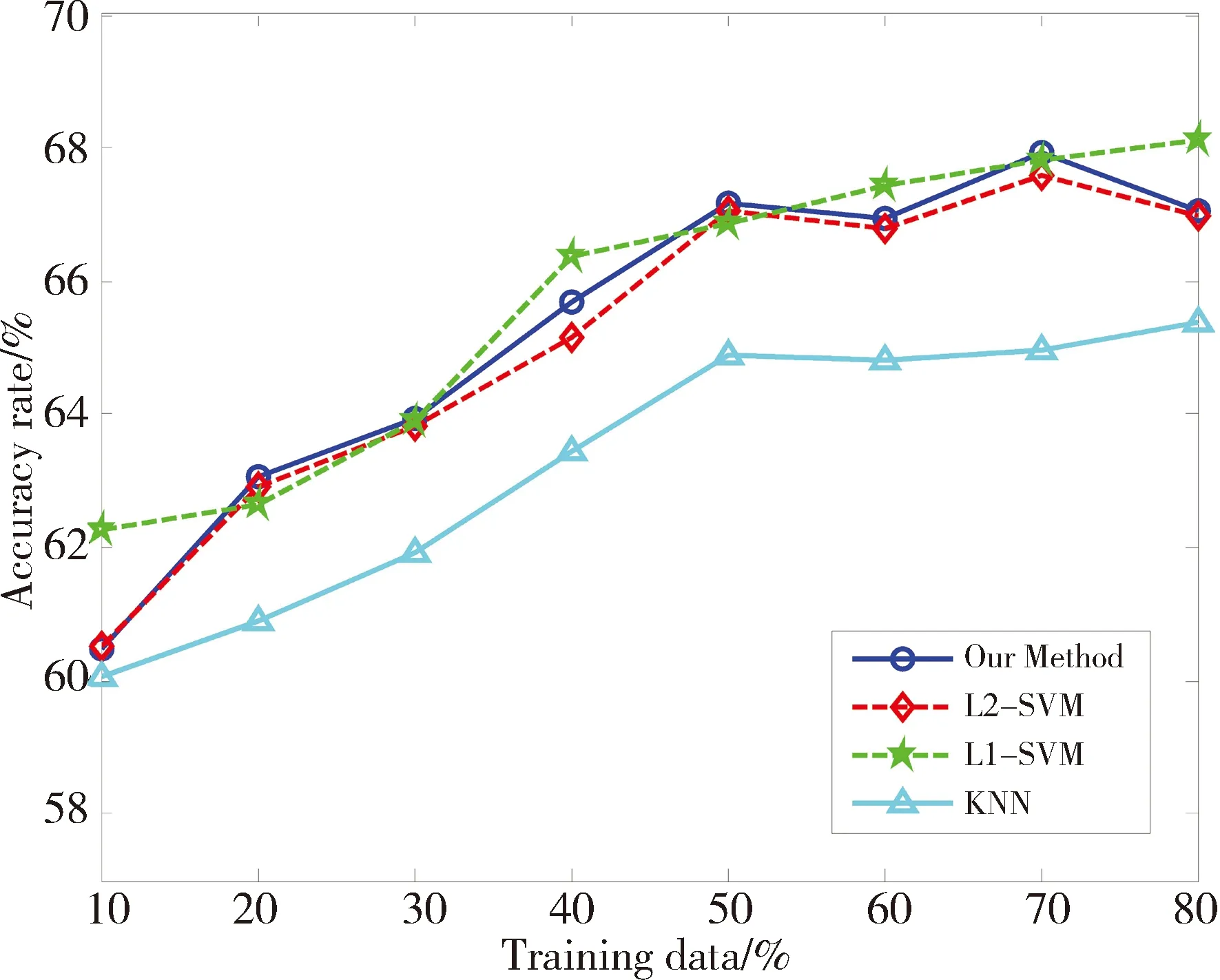
(e)Liver

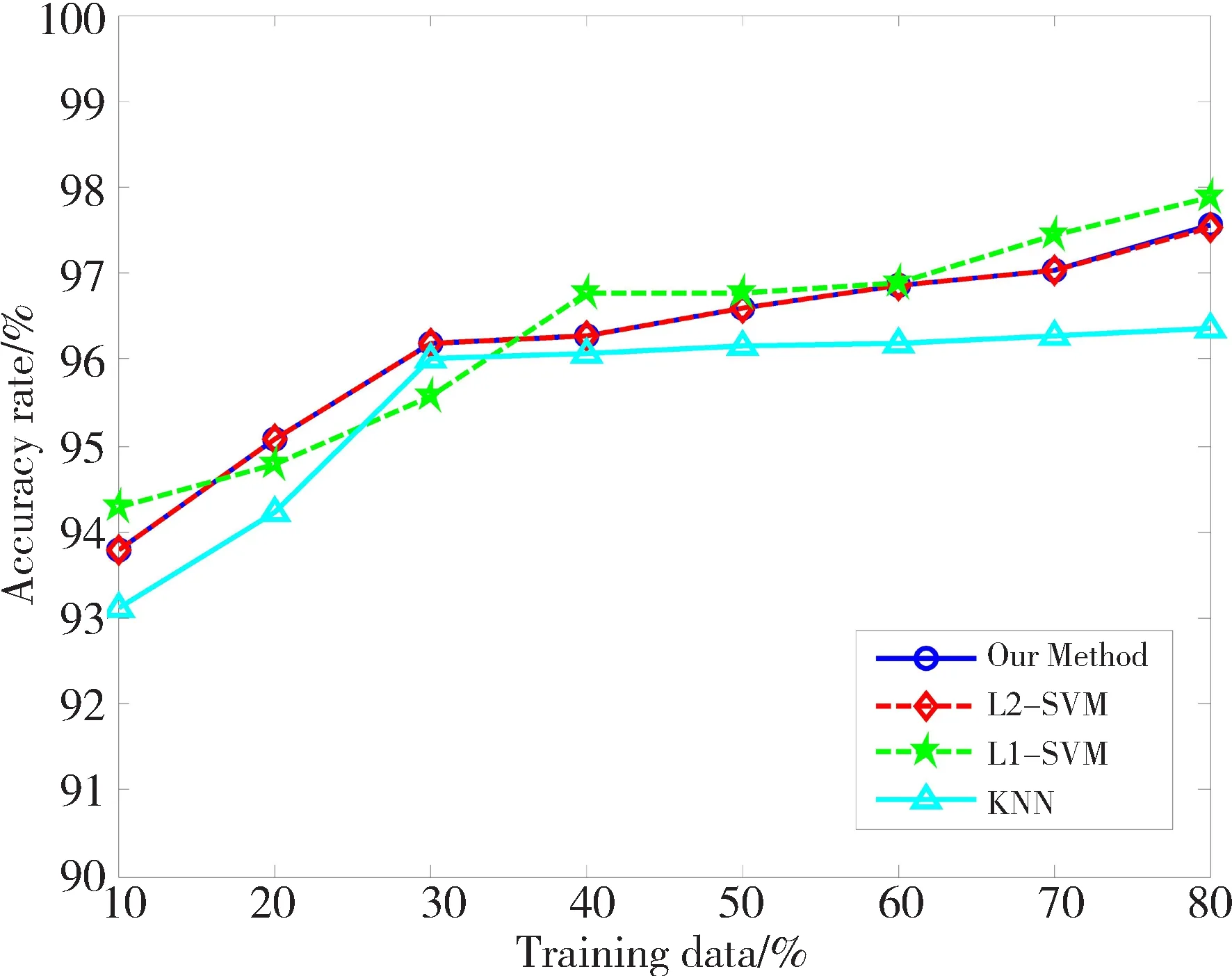
(f)Wdbc

从图3可以得到以下几点信息： 1)随着训练样本数目的增加，分类精度逐步提高，这是由于训练样本提供的特征信息决定着分类器的性能，特征信息越多，训练出的分类器识别效果越好；2)对于6个数据集，KNN算法的分类精度明显低于SVM，因为SVM引入核函数，对提高算法的分类精度起到关键的作用；3)基于传统RM界的L2-SVM算法和文中改进的算法的分类精度都呈现共同的特征，即针对不同的测试数据，2种方法在6个数据集中得到的分类精度变化趋势一致，数据集Breast、Ionosphere、Wdbc的分类正确率基本吻合，其余3个数据集分类正确率差别不明显。本文改进算法没有影响L2-SVM的分类精度。

3.2计算效率比较

为比较算法的计算效率，针对L2-SVM算法的模式选择，分别计算基于传统RM界和本文改进的RM界的算法执行时间。数据仍采用表1中给出的6个数据集，每个数据集随机选取60%作为训练数据，40%作为测试数据，其实验结果如图4所示。可知，与传统RM界的模式选择相比，本文改进算法的计算效率明显提高。其中，计算效率提高最多的是Pima数据集，提高2倍，最少也提高1倍，如Breast数据集的实验结果。RM界中的最小包含球半径需要求解二次规划问题，使得每次迭代过程消耗较大的计算量。相反的，文中改进的RM界，在不影响SVM分类精度的同时，利用样本间的最大距离逼近半径的求解，使得改进的算法能以较高的效率完成对参数的选择，这更有利于SVM在实际中的应用。

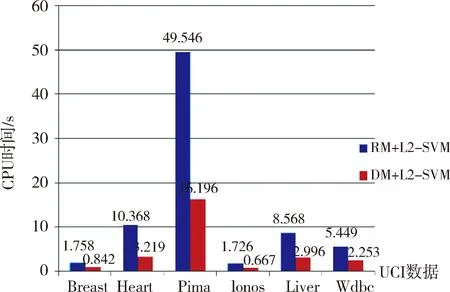
图4　基于不同算法的计算时间

4结论

文中算法与基于RM界的L2-SVM模式选择相比，用样本间的最大距离逼近半径R的求解，避免迭代过程中求解二次规划问题，减小了模式选择算法的计算量。实验结果表明，文中改进算法与传统的基于RM界的L2-SVM模式选择相比，不仅获得相差较小的算法精度，而且明显降低了计算消耗。未来工作中，将进一步提高该方法的分类性能与泛化能力，使其更广泛地应用到其他模式选择方法中。

参考文献

一铵市场观望氛围较浓，目前企业报价高位坚挺，厂家新单签订情况一般，主要发运前期预收，在磷复肥会议召开之前，一铵暂无下滑预期，维持平稳运行。湖北地区55%粉主流出厂价2350元/吨，58%粉2400元/吨，60%粉2500元/吨；河南地区55%粉出厂价2350元/吨，成本压力较大，企业报价高位盘整；云南主产区55%粉主流出厂价2300元/吨，58%粉主流出厂价2400元/吨，60%粉出厂报价2500元/吨；安徽地区55%粉主流出厂2300元/吨，供应紧张，新单成交缓慢；山东地区55%粉一铵到站价2550元/吨。

[1]Corinna Cortes, Vladimir Vapnik.Support-vector Networks[J]. Machine Learning, 1995, 20(3): 273.

[2]丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报(自然科学版), 2011, 40(1): 2.

[3]Maldonado S, Weber R, Famili F. Feature Selection for High-dimensional Class-imbalanced Data Sets using Support Vector Machines [J]. Inf Sci, 2014, 286: 228.

[4]Tian Yingjie, Ping Yuan. Large-scale Linear Nonparallel Support Vector Machine Solver [J]. Neural Networks, 2013, 50: 166.

[5]Reitmaier T, Sick B. The Responsibility Weighted Mahalanobis Kernel for Semi-Supervised Training of Support Vector Machines for Classification [J]. Inf Sci, 2015, 323: 179.

[8]Zhao M Y, Ren J, Ji L P, et al. Parameter Selection of Support Vector Machines and Genetic Algorithm based on Change Area Search[J]. Neural Computing and Applications, 2012, 21(1): 1.

[9]魏峻. 一种有效的支持向量机参数优化算法[J].计算机技术与发展, 2015, 25(12): 97.

[10]Shaoa C, Paynabarb K, Kima T H. Feature Selection for Manufacturing Process Monitoring using Cross Validation [J]. Manuf Syst, 2013, 32: 550.

[11]CAWLEY G C.Leave-one-out Cross-validation based Model Selection Criteria for Weighted ls-svms [C]//IEEE World Congress on International Joint Conf erence on Neural Networks. Vancouver, BC：IEEE, 2006: 1661-1668.

[12]Chapelle O, Vapnik V. Choosing Multiple Parameters for Support Vector Machines [J]. Machine Learning, 2002, 46(1): 131.

[13]Kaibo Duan, Sathiya Keerthi, Aun Neow Poo.Evaluation of Simple Performance Measures for Tuning SVM Hyper Parameters [J]. Neurocomputing, 2003, 51: 41.

[14]刘昌平, 范明钰, 王光卫,等. 基于梯度算法的支持向量机参数优化方法[J]. 控制与决策, 2008, 23(11): 1291.

[15]Huyen Do, Alexandros Kalousis. Convex Formulations of Radius-margin based Support Vector Machines[J]. JMLR Workshop and Conference Proceedings, 2013, 28(1): 169.

[16]Tax D M J, Duin R P W. Support Vector Data Description [J]. Mach Learn, 2004, 54(1): 45.

(编校：饶莉)

Model Selection for 2-norm Support Vector Machine Based on Improved RM Bound

YANG Xiaohuan1, WANG Xiaoming2*, TIAN Yong2,SONG Jingping3

(1.SchoolofScience,XihuaUniversity,Chengdu610039China;2.SchoolofComputerandSoftwareEngineering,XihuaUniversity,Chengdu610039China；3.TibetFeiyueIntelligentTechnologyCo.,Ltd.，Lasa850000China)

Abstract:Calculating the radius of radius-margin (RM) bound by solving the quadratic programming adds the computational overload. In order to solve this problem, we construct a new RM bound which approximates the radius by using the maximum pairwise distance over all points. Then based on new RM bound, the model selection of 2-norm SVM (L2-SVM) was conducted, and automatically adjusted parameters by employing the gradient descent algorithm. Finally, the classification accuracy and computational efficiency of the algorithm were discussed through simulation experiments.The experimental results show that the classification accuracy of the proposed algorithm is not significantly changed compared with the model selection based on RM bound, but the computational efficiency is improved at least one fold.

Keywords:model selection; support vector machine; radius-margin bound; gradient descent algorithm; radius-margin(RM) bound

收稿日期：2016-01-06

基金项目：国家科技支撑计划项目西藏自然科学博物馆数字馆关键技术研究及集成示范(2011BAH26B01)；四川省教育厅自然科学重点项目(11ZA004)；西华大学研究生创新基金项目(ycjj2014032)。

*通信作者：王晓明(1977—)，男，副教授，博士，主要研究方向为机器学习与模式识别。E-mail：wangxmwm@gmail.com

中图分类号：TP181

文献标志码：A

文章编号：1673-159X(2016)03-0057-6

doi:10.3969/j.issn.1673-159X.2016.03.012

·计算机软件理论、技术与应用·