AunS(n=2～8)团簇结构和稳定性的密度泛函研究

马想平，郭建军

(西华大学理学院，四川 成都　610039)



·基础学科·

AunS(n=2～8)团簇结构和稳定性的密度泛函研究

马想平，郭建军*

(西华大学理学院，四川 成都610039)

摘要：采用密度泛函理论的PW91PW91方法，在相对论有效原子实势(RECP)近似情况下，系统研究混合小团簇AunS(n=2～8)团簇的几何结构、稳定性、电子特性。通过全优化计算，给出相应团簇的基态稳定几何构型及同分异构体；通过计算平均结合能Eb、HOMO与LUMO间的能级间隙Eg和二阶差分能量Δ2E，对基态AunS团簇的稳定性和电子特性进行研究。结果表明：基态结构既有平面结构又有立体结构，并且具有不同的对称性；随着团簇的增大，热稳定性越高，Au8S团簇具有最高的热稳定性；Au6S团簇具有最高的化学稳定性；偶数原子团簇比奇数原子团簇更稳定。本研究可为Au-S团簇的实验研究提供理论参考。

关键词：密度泛函理论；PW91PW91；Au-S团簇；电子特性

原子分子团簇被视为凝聚态物质的初始形态，在各种物质从原子分子向块状材料转变过程中起着非常重要的作用，对其进行研究有助于我们认识大块凝聚物质的某些性质和规律。在过去的几十年里，人们对纯金属元素团簇进行了广泛地研究，并发现许多新奇的现象，如纳米Au团簇在低温下对CO具有良好的催化性能，理论和实验方面的科学研究还证明团簇的物理性质与其构成原子的种类存在密切的关系[1-16]；因此金属与非金属的二元混合团簇的研究越来越受到人们的重视。对于Au的二元团簇的研究，目前涉及到了常见的Fe、Mn、Zn、Cu等金属，而对Au与S的二元团簇的研究却较少。本文在相对论有效原子实势(RECP)近似下，采用密度泛函理论的PW91PW91方法，对AunS(n=2～8)团簇进行全优化计算，搜索它们的基态同分异构体结构，分析其稳定性和电子特性，为Au-S团簇的实验研究提供理论参考。

1计算方法

我们采用密度泛函PW91PW91方法，Au和S原子分别使用Def2-TZVPP和LanL2DZ基组，对不同对称性及自旋态的AunS(n=2～8)结构进行几何优化计算，然后进行频率分析，如果计算所得的频率数值全部为正，说明该结构对应势能面上的一个极值点，表明这种构型是稳定结构，若有负值出现，就表明该结构是不稳定构型或是一种相应的过渡态。该方法的正确性已用Au2、S2进行了检验，其结果如表1所示，本文计算值与实验结果一致。

表1　Au2、S2团簇的键长和电子特性

注：Refs. [17]a，Refs. [18]b。

2计算结果与讨论

2.1稳定的几何构型

S和Au原子之间的平均键长、最小键长、最大键长和配位数如表2所示。

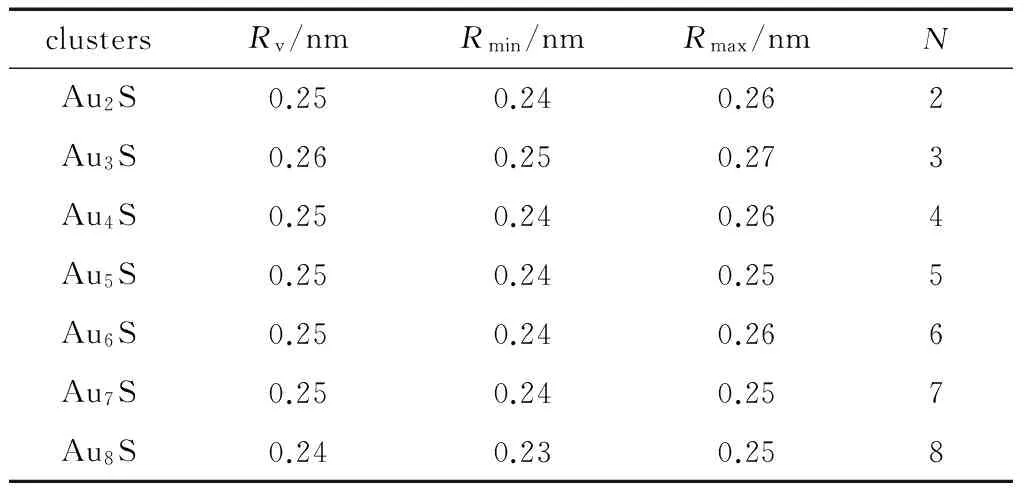
表2　S和Au原子之间的平均键长(Rv)、最小键长(Rmin)、

AunS(n=2～8)团簇的基态同分异构体几何构型如图1所示。

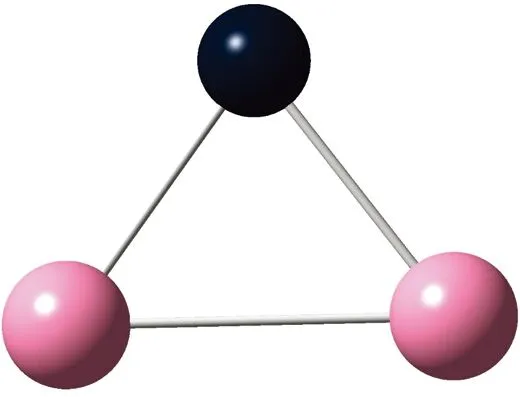
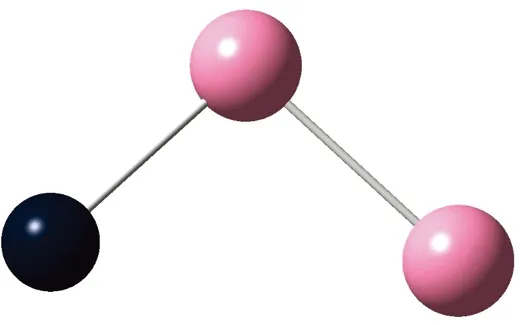
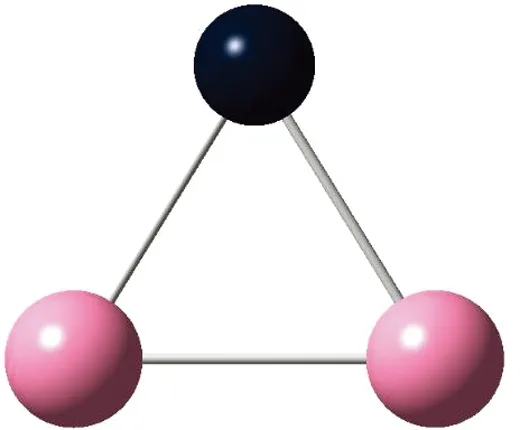
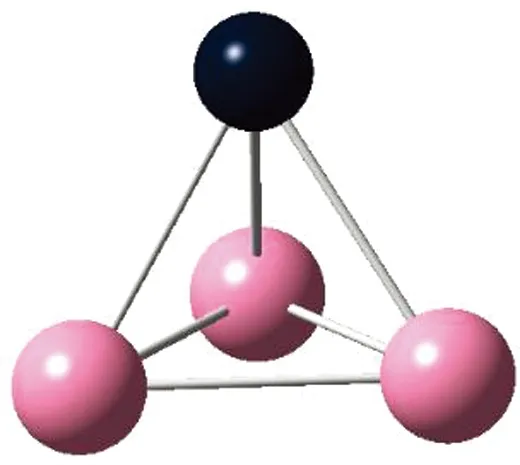
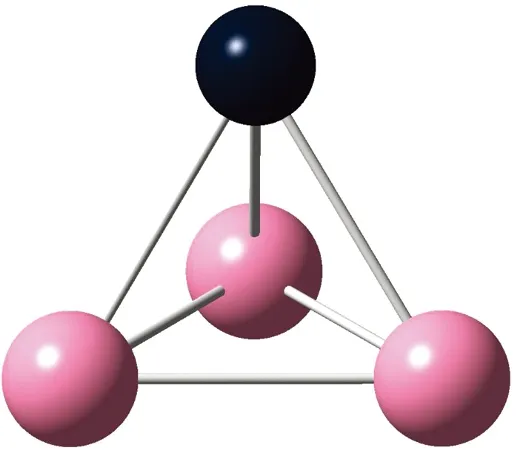
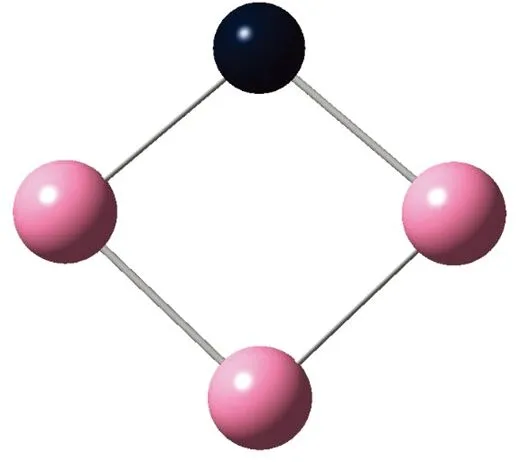
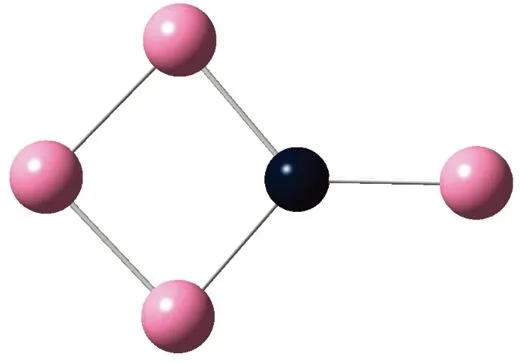
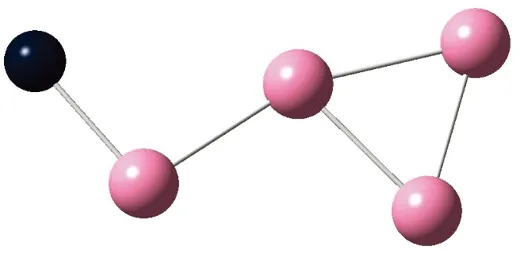
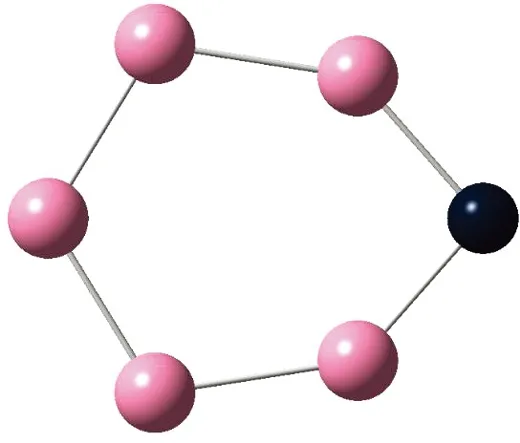
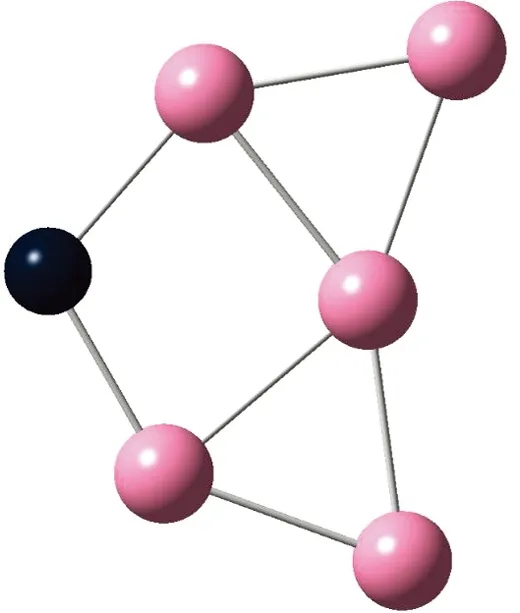
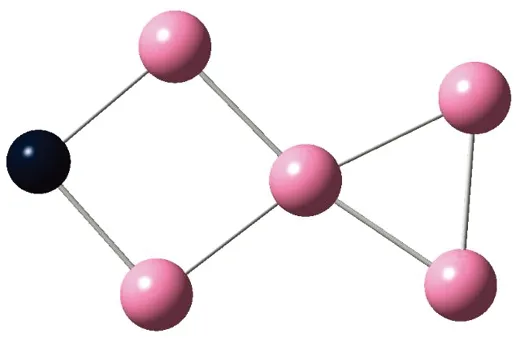
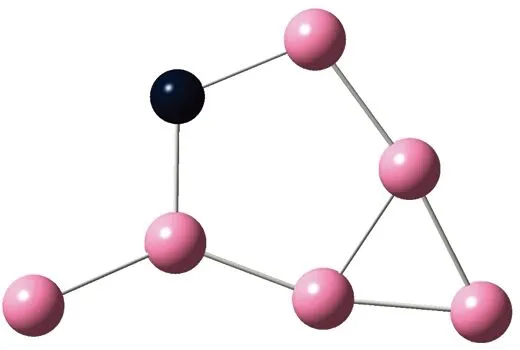
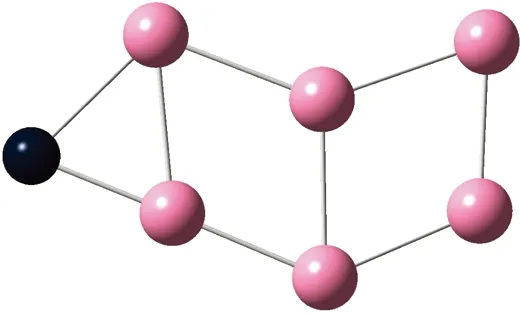
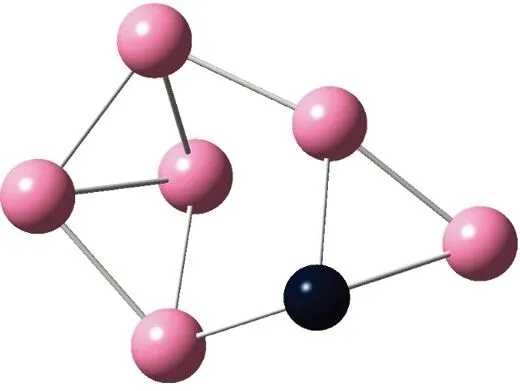
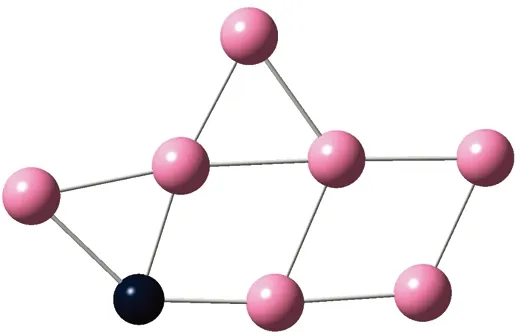
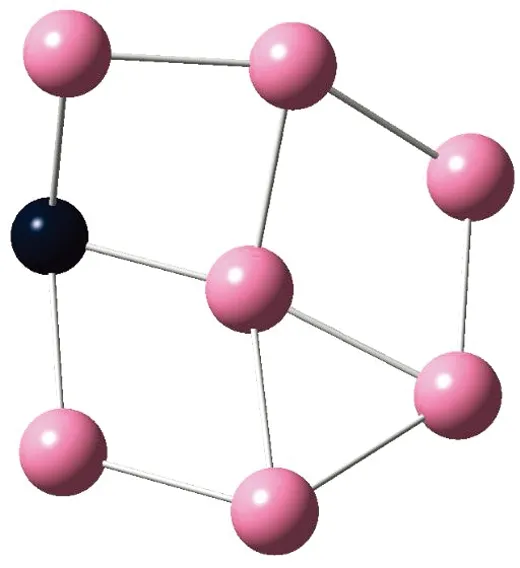
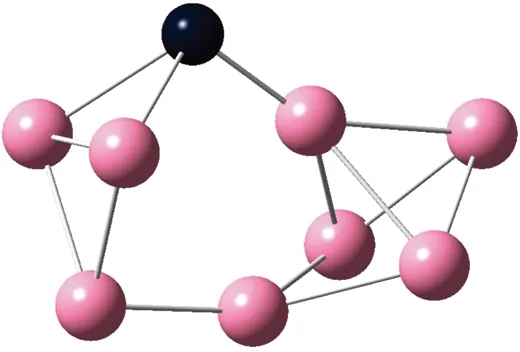
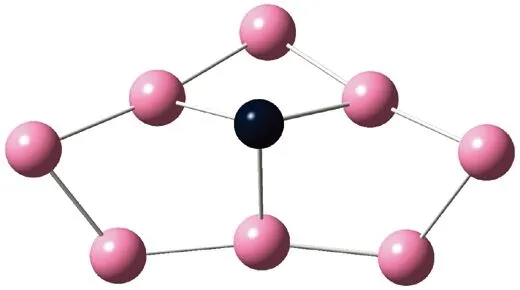
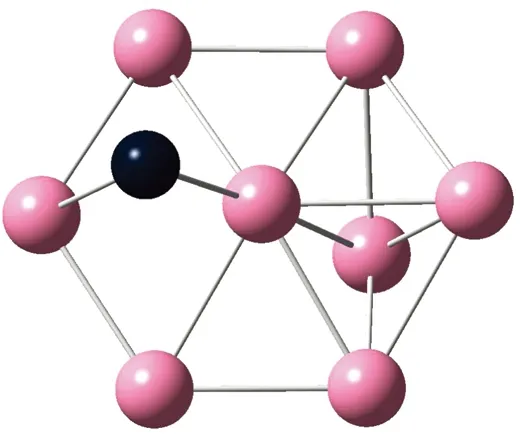
CS, 7, 0.25 eV8d

通过对AunS(n=2～8)团簇的构型进行全优化计算，得到图1中所示的基态同分异构体结构，图 1中，粉红色球代表Au原子，黑色球代表S原子，a、b、c、d代表基态的不同同分异构体。图下面的参数分别表示对称性、自旋态、基态能量。从图1中可看出，Au2S、Au5S均为平面结构，Au3S、Au4S、Au6S和 Au7S既有平面构型也有立体构型，Au8S都是空间立体结构。Au3S 的3a、3b、3c为空间立体构型，3d为平面结构。Au4S的4a、4d是空间立体结构，4b、4c则是平面构型。对Au2S，2a、2c、2d对称性为C2V，2b为CS对称，其中，2c为线形，2a、2b、2d为三角形，2a、2b自旋态为7，2c、2d为5。Au3S，3a、3b、3c为CS，3d为C2V对称，3a、3b、3c为锥形，3d为四边形，自旋态均为6。在Au4S中，4b、4c为平面构型，4a、4d为空间立体结构，自旋态均为7，4a、4b、4c为CS对称，4d为C1对称。Au5S均为平面构型，5a、5b、5c为六边形，5d为铲形，对称性均属于C2V，自旋态均为6。对Au6S，6a、6b、6d属于C1对称，6c为CS对称，6a为平面结构，6b、6c、6d为空间构型，自旋态均为7。Au7S中，7a、7d为立体构型，7b、7c为平面构型，S原子位于顶点处，7a自旋态为4，7b、7c、7d自旋态为6，7a、7b为C2V、CS对称，7c、7d为C1对称。从图1可以看出，虽然基态AunS(n=2-8)的同分异构体的构型相同，但是对称性、电子态及能量各不相同，Au7S的基态电子态为二重态，Au3S、Au5S为三重态。Au-S键长的计算值为0.26 nm，大于表1列出的Au2和S2的键长理论值与实验结果。表2是本文计算得到的Au和S原子之间的最小键长(Rmin)、最大键长(Rmax)和随Au原子派位数数(N)增加的平均键长(Rv)。从表2可以看出，随着n的递增，Rv、Rmin、Rmax也不相同，Rmin为0.23 nm，Rmax为0.27 nm，同样，随着n的增加，基态AunS团簇的平均键长也表现出先增大后减小的趋势，只是在n=3时，Rv有最大值。从图1可以看出，Au5S为平面构型，对称性为C2V，自旋态为6，并且Au5S为三重态构型。

2.2电子特性

利用平均结合能Eb、HOMO与LUMO间的能级间隙Eg和二阶差分能量Δ2E对基态AunS团簇的电子特性进行研究。

对于基态AunS团簇，其平均结合能计算公式可以表示为

Eb[AunS]=(nE[Au]+ E[S]-E[AunS])/(n+1)。

(1)

其中，E[Au]、E[S]、E[AunS]分别表示基态Au原子、S原子和AunS团簇的能量。图2显示了Eb随团簇大小的变化曲线，从图2可以看出随着n的增加Eb也呈现出不断增加的趋势，且在n=8时Eb值最大，即Au8S的原子结合能最大，这意味着Au8S团簇具有较高的热稳定性。

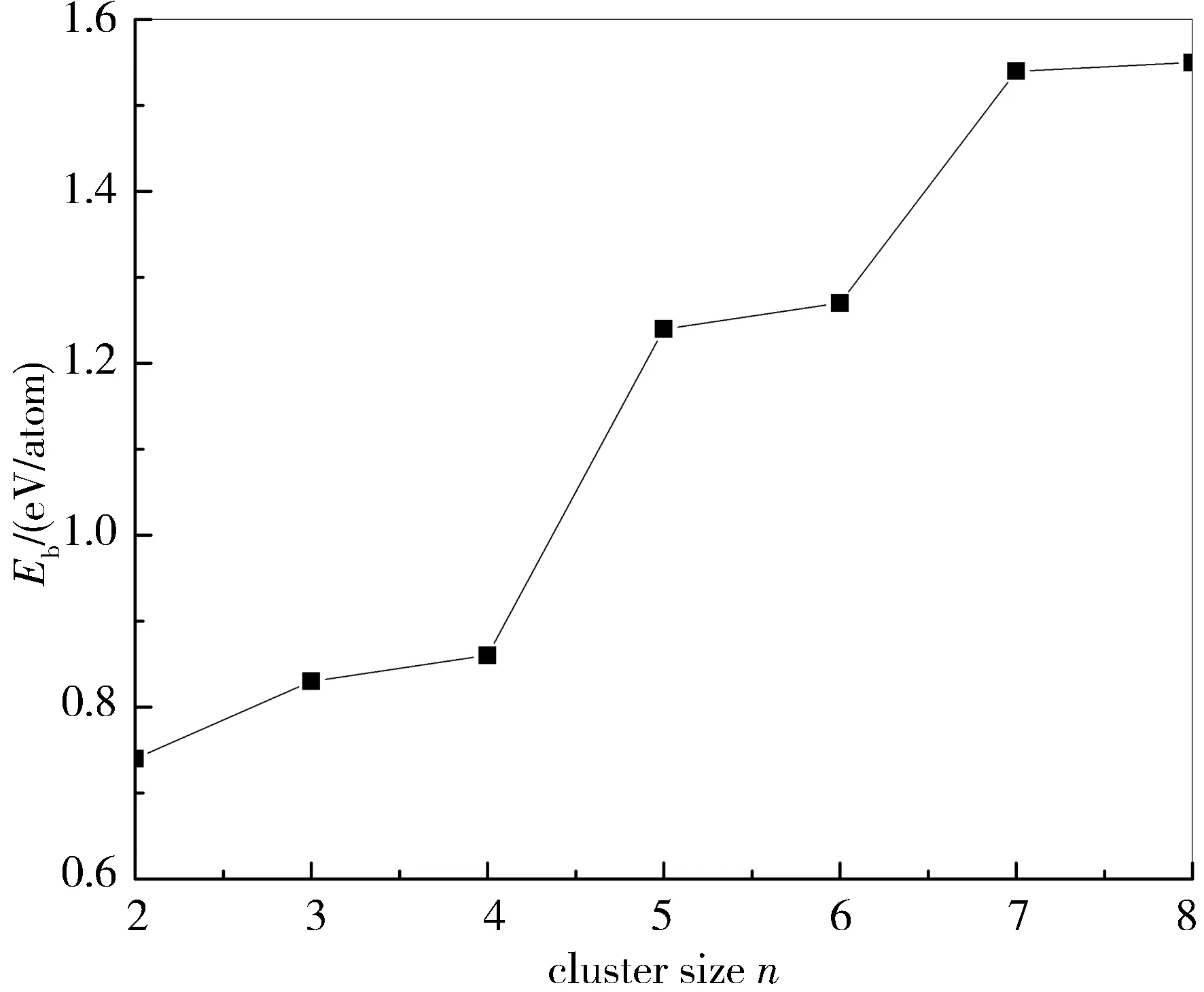
图2　AunS(n=2～8)团簇基态构型的平均

HOMO与LUMO之间的能级间隙是反映价电子从HOMO向LUMO跃迁能力的重要参数，在一定程度上反映了团簇化学反应的活性。如果能级间隙越大，化学活性越低；能级间隙越小，化学活性越高。图3示出AunS(n=2～8)基态稳定结构的能级间隙Eg随n的变化关系，可以看出Au6S团簇具有较高的化学稳定性。

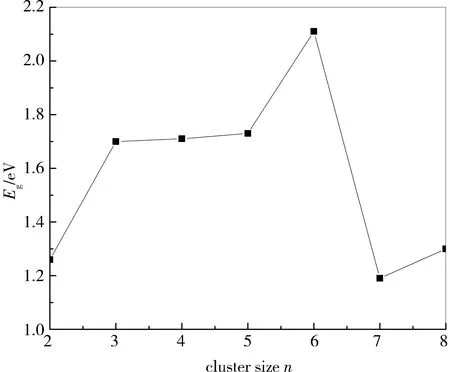
图3　AunS(n=2～8)基态构型的能级间隙Eg变化趋势

团簇的稳定性除了与构成该团簇的原子有关外，还与包含原子的数目有关。理论上，它可利用团簇的能量二阶差分来确定。AunS (n=2～8)团簇的Δ2E计算公式如下：

Δ2E [AunS]=E[Aun+1S]+

E[Aun-1S]-2 E[AunS]。

(2)

图4给出了AunS(n=2～8)基态稳定结构的Δ2E随n的变化关系。可以看出Δ2E的值随n的递增呈现奇偶震荡的变化趋势，这意味着偶数原子团簇比奇数原子团簇更稳定。

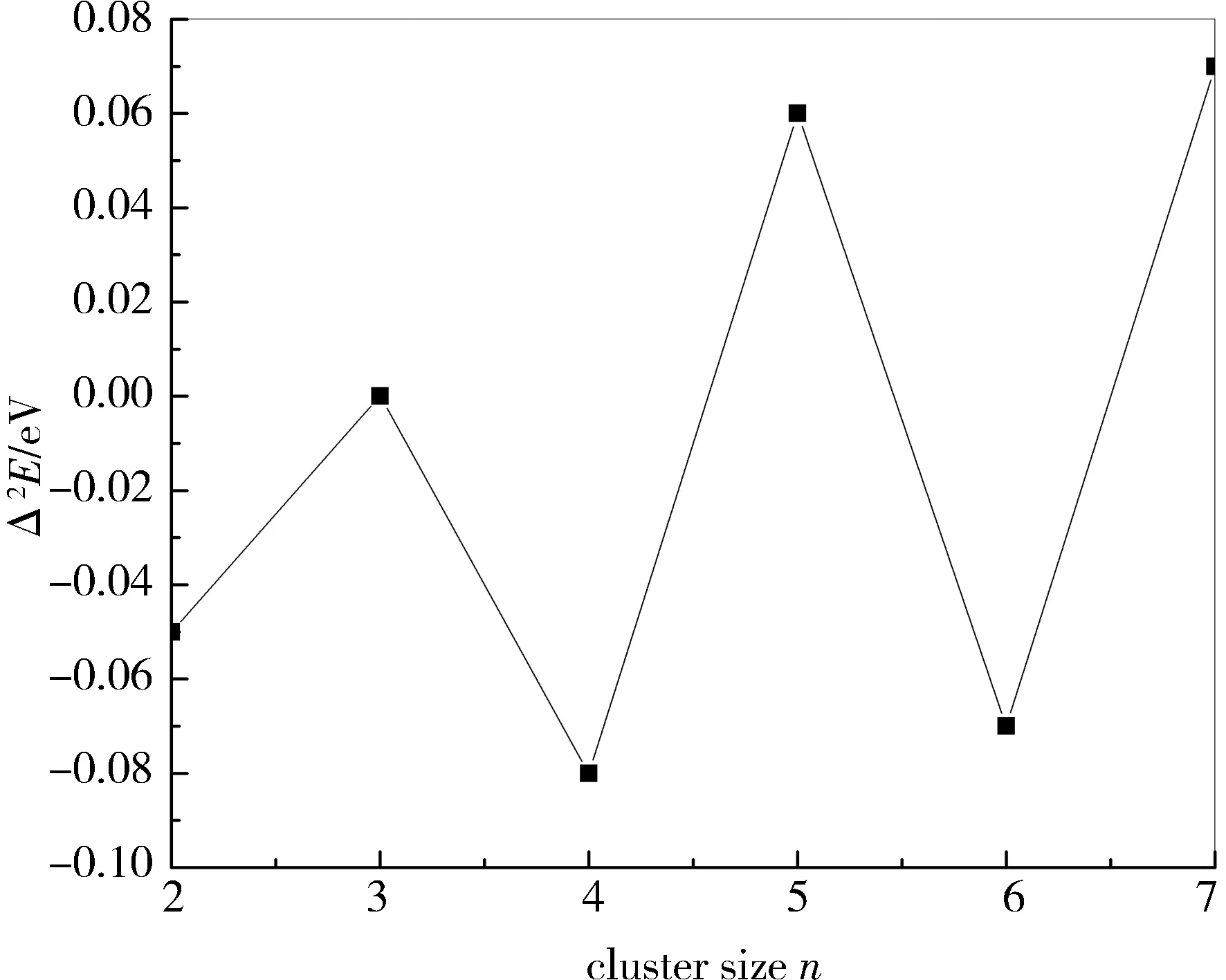
图4　AunS(n=2～8)团簇基态构型的二阶差分能量

3结论

本文基于密度泛函PW91PW91方法，研究了AunS(n=2～8)团簇的几何构型和基态构型的能级间隙、原子结合能、二阶差分能量。研究结果表明：它的基态结构既有平面结构又有立体结构，并且具有不同的对称性；AunS团簇随着原子数的增大，热稳定性越高；基态Au6S团簇的化学稳定性比其他AunS团簇高，二阶差分能量表现出奇偶震荡，即偶数原子团簇比奇数原子团簇更稳定。

参考文献

[1]Zhao J, Chen X, Sun Q, et al. Critical Size for Magnetic Nonmagnetic Transition in Transition-metal Clusters[J]. Eur Lett, 1995,32(2):113.

[2]Beckmann H , Bergmann G. Mystery of the Alkali Metals: Giant Moments of Fe and Co, on and in Cs Films[J].Phys Rev Lett, 1999,83(12):2417.

[3]Gambardella P , Dhesi S S , Gardonio S , et al. Localized Magnetic States of Fe,Co, and Ni Impurities on alkali Metal Films[J].Phys Rev Lett, 2002,88(4):047202.

[4]Bagayoko D, Brener N, Kanhere D, et al. Electronic and Magnetic Properties of Manganese Impurities in Aluminum[J].Phys Rev B, 1987,36(17):9263.

[5]Die Dong, Kuang Xiao-yu.Theoretical Study of Geometrical Structures,and Electronic Properties for Co@Aun(n=1～8) Clusters[J]. Journal of Atomic and Molecular Physics, 2012,29(2):267.

[6]郑本霞, 迭东, 王玲, 等. 金团簇二维到三维的结构转变和电子特性的理论研究[J]. 西华大学学报(自然科学版), 2014，33(5):37.

[7]Die Dong, Kuang Xiao-yu, Zhu Bing ,et al . Geometrical, Electronic,and Magnetic Properties of Small AunSc(n=1～8) Clusters[J]. Physica B, 2011(406):3160.

[8]Die Dong, Kuang Xiao-yu , Guo Jian-jun , et al . Geometries, Stabilities,and Magnetic Properties of Cr@Aun(n=1～8) Clusters: Density Functional Theory Study[J]. Physica A, 2010(389): 5216.

[9]Die Dong, Kuang Xiao-yu , Guo Jian-jun , et al. First-principle Study of AunFe(n=1～7) Clusters[J].Journal of Molecular Structure: THEOCHEM, 2009(902):54.

[10]Janssens E, Tanaka H , Neukermans S , et al. Electron Delocalization in AunXm(X=Sc,Ti,Cr,Fe) Clusters: A Density Functional Theoryand Photofragmentation Study[J].Phys Rev B, 2004,69(8): 085402.

[11]王红艳,李喜波,唐永建，等.AunXm(n+m=4,X=Cu,Al,Y)混合小团簇的结构和稳定性研究[J].物理学报,2005,54(8):3565.

[12]Tanaka H, Neukermans S, Janssens E, et al. Density Functional Study on Structure,and Stability of Bimetallic AunZn(n≤6) Clusters and Their Cations[J]. J Chem Phys, 2003,119(14): 7115.

[13]Yuan D W , Wang Y , Zeng Z. Geometric, Electronic,and Bonding Properties of AunM (n=1～7,M =Ni,Pd,Pt) Clusters[J]. J Chem Phys, 2005,122(11):114310.

[14]毛华平,王红艳,朱正和，等.AunY(n=1～9)掺杂团簇的结构和电子性质研究[J].物理学报,2006, 55(9):4542.

[15]Guo Jian-jun , Yang Ji-xian , Die Dong. Abinitio Study of Small AunY2(n=1～4)clusters[J]. Physcia B, 2008,403(21/22):4033.

[16]Becke A D. Density-functional Thermochemistry.III.The Role of Exact Exchange[J]. The Journal of Chemical Physics, 1993(98):5648.

[17]Mao Hua-ping , Wang Hong-yan , Ni Yu , et al. Geometry and Electronic Properties of Aun(n=2～9) Clusters[J]. Phys, 2004,53(6):1766.

[18]Bai Yu-lin , Chen Xiang-rong , Yang Xiang-dong , et al. Structrues of Small Sulfur Clusters Sn(n=2-8) from Langevin Molecular Dynamics Methods[J]. The Journal of Chemical Physics, 2003,19(12):1102.

(编校：叶超)

Structures and Stability of AunS (n=2～8) Clusters: a Density Functional Study

MA Xiangping, GUO Jianjun*

(SchoolofScience,XihuaUniversity,Chengdu610039China)

Abstract:The geometry, stability, and electronic properties of the small clusters AunS (n=2～8) were studied systematically based on density functional method PW91PW91 and an effective core potential basis set. Some corresponding stable ground state geometries and isomers were given. The stability and electronic property were analyzed by HOMO-LUMO gap and the second-order difference of energy. The results show that the ground state structures of AunS clusters are planar and 3D configuration. The caloric stability of AunS clusters increases with the raise of size and the Au8S is maximum. The AunS cluster with odd n are more stable than that with even n. This work would be useful for Au-S clusters experimental study.

Keywords:density functional theory; PW91PW91; Au-S Clusters; electronic properties.

收稿日期：2015-11-06

*通信作者：郭建军(1964—)，男,教授, 硕士,主要研究方向为分子结构与光谱。E-mail: xhu_gjj @163.com.

中图分类号：O641

文献标志码：A

文章编号：1673-159X(2016)03-0071-4

doi:10.3969/j.issn.1673-159X.2016.03.015