表面织构化径向轴承的弹流润滑研究

于如飞，陈　渭

(西安交通大学现代设计及转子轴承系统教育部重点实验室, 陕西 西安　710049)



表面织构化径向轴承的弹流润滑研究

于如飞，陈渭

(西安交通大学现代设计及转子轴承系统教育部重点实验室, 陕西 西安710049)

摘要：为研究表面织构和轴承表面弹性变形对径向滑动轴承润滑性能的影响，利用Winkler弹性基础模型计算轴承表面的变形量，采用有限差分法求解经典雷诺方程，最终计算并对比含表面织构和无织构情况以及柔性和刚性条件下的轴承润滑性能。数值模拟结果表明：与轴承表面的弹性变形相比，表面织构对径向轴承静特性的影响更加显著，且织构可以明显改变油膜压力的分布情况；此外，织构在轴承上的分布位置对轴承性能也有不同的影响作用，分布在压力上升区域的织构对轴承特性有正面的影响，分布在压力下降区域的织构对轴承特性有负面影响。

关键词：表面织构化；径向轴承；弹流润滑；Winkler弹性基础模型

表面织构化已经被证明是一种改善相互运动表面摩擦学性能的有效技术手段。在过去几十年间，出现了大量关于表面织构理论和试验的研究文献，涉及的内容主要包括织构在滑动摩擦副表面中的应用及参数优化[1-3]，织构几何形状对表面摩擦学性能的影响[4-6]，织构分布形式和分布位置的影响[7-9]，以及织构对流体动力润滑综合特性的影响[10- 11]等。此外，理论研究所使用的方法依据流体控制方程的不同，主要有计算流体动力学(CFD方法)[5, 8]和个人编程求解Reynolds方程[4, 6-7]2大类。CFD方法一般借助商业软件实现，其优点是可以显示完整的流场分布且容易上手，缺点就是建模、网格划分以及求解设置等过程比较烦琐，计算效率相对较低。Reynolds方程和有限差分法仍然是目前应用最广泛的表面织构流体润滑研究手段。

径向滑动轴承在各种工业用途中被大量使用，例如动静压滑动轴承、高速主轴-转子系统以及含间隙铰接副的多体系统等。众所周知，轴承表面或轴瓦的弹性变形会对径向轴承的润滑性能产生重要影响[12-15]，特别是对于重载和轴瓦材料弹性模量较小的情况。针对传统意义上的点或线接触条件下的弹性流体动力润滑研究相对比较成熟[16-17]，然而，径向轴承的轴与轴套之间的接触问题并不真正属于接触力学的研究范畴。另外，这类问题中的轴承表面弹性变形的求解方法大多为有限元法和柔度矩阵法[13-14, 18]，其缺点在于计算效率低和资源消耗大。Winkler弹性基础模型已经被成功应用于分析柔性径向轴承的流体动力润滑特性[19]，然而在先前的研究工作中，轴承是被作为无限长或无限短的情况来处理，这显然与实际情形极不相符；因此，对三维径向轴承弹性变形的精确求解，并进一步分析真实条件下的轴承润滑性能是非常必要的。除此之外，要想探讨表面织构在轴承表面的排列布局对轴承性能的影响作用，也必须在三维的几何模型中才可以实现。

针对有限长径向滑动轴承，本文在同时考虑轴承表面弹性变形和表面织构双重影响的情况下，利用有限差分法求解雷诺方程，并进一步通过大量的数值模拟，分析表面织构参数和分布形式对轴承流体动力润滑性能的影响。

1模型与方程

在径向滑动轴承弹流润滑问题的求解中，主要涉及的方程有弹性变形方程和流体流动控制方程。本文选择最常用的Reynolds方程作为流体控制方程，将Winkler弹性基础模型作为计算轴承表面弹性变形的方程。

1.1Reynolds方程

处于完全流体动力润滑区域的流体控制方程可以用著名的Reynolds方程来描述，如图1所示。在笛卡尔坐标系中，轴承沿径向的润滑油膜厚度分布用h来表示，那么对于运行在稳态条件下的轴承，其油膜压力分布由如下方程所控制：

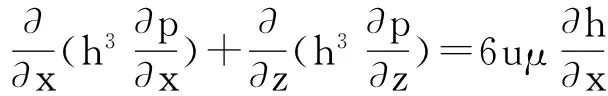
(1)

式中：p为油膜压力，Pa；u为轴的线速度，m/s；μ为润滑油动力黏度，Pa·s；x表示轴承的圆周方向，y表示半径方向，z表示轴向。含有表面织构径向轴承的润滑油膜厚度可表示为

h=hs+ht。

(2)

式中：ht为微凹坑深度；hs为无织构情况下的轴承油膜厚度，可表示为

hs=c[1+εcos(θ-Φ)]。

(3)

其中：c为轴承半径间隙，mm，其值等于轴承半径R与轴半径r之差；ε为轴承偏心率，等于轴承偏心距e与半径间隙之商；θ为圆周方向角度坐标，(°)；规定轴承正上方为起始测量点，以轴颈的转动方向为正向，Ф为轴承偏位角。在利用数值方法求解Reynolds方程的过程中，使用普遍认为比较合理的Reynolds边界条件，为：

p=0(θ=Φ)；

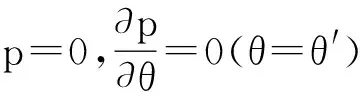
(4)

式中θ′表示油膜破裂位置处的角度坐标。

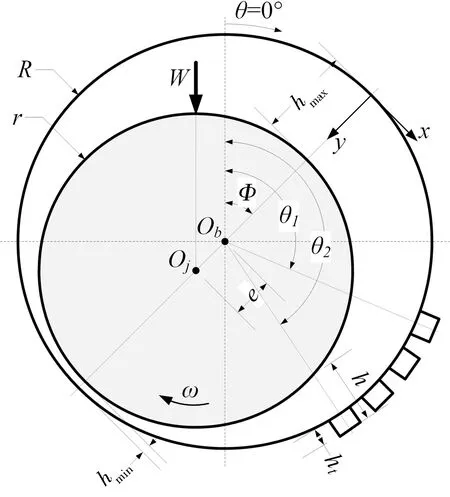
图1　织构化径向轴承

图2示出含织构轴承表面沿圆周方向的展开情况，其中，单个的矩形微凹坑在周向和轴向的宽度分别用Lc和Lz表示，θ1为织构群在圆周方向的起始位置坐标，θ2为对应的终止位置坐标，L表示轴承宽度，mm。织构在轴承表面的三维分布情况如图3所示，其中，圆周方向和轴承轴向的织构数量分别用Nc和Nz表示。

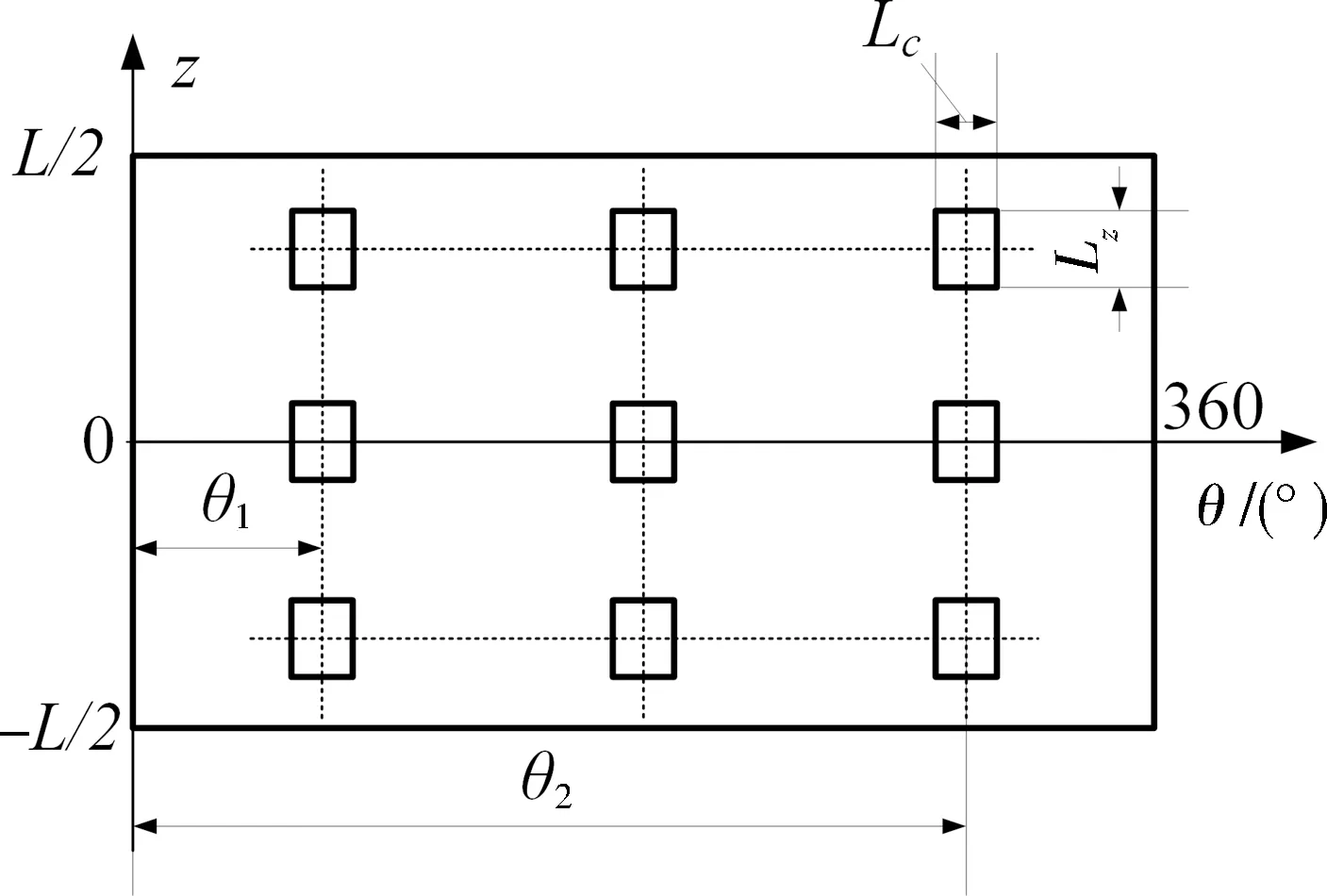
图2　含织构的轴承表面展开

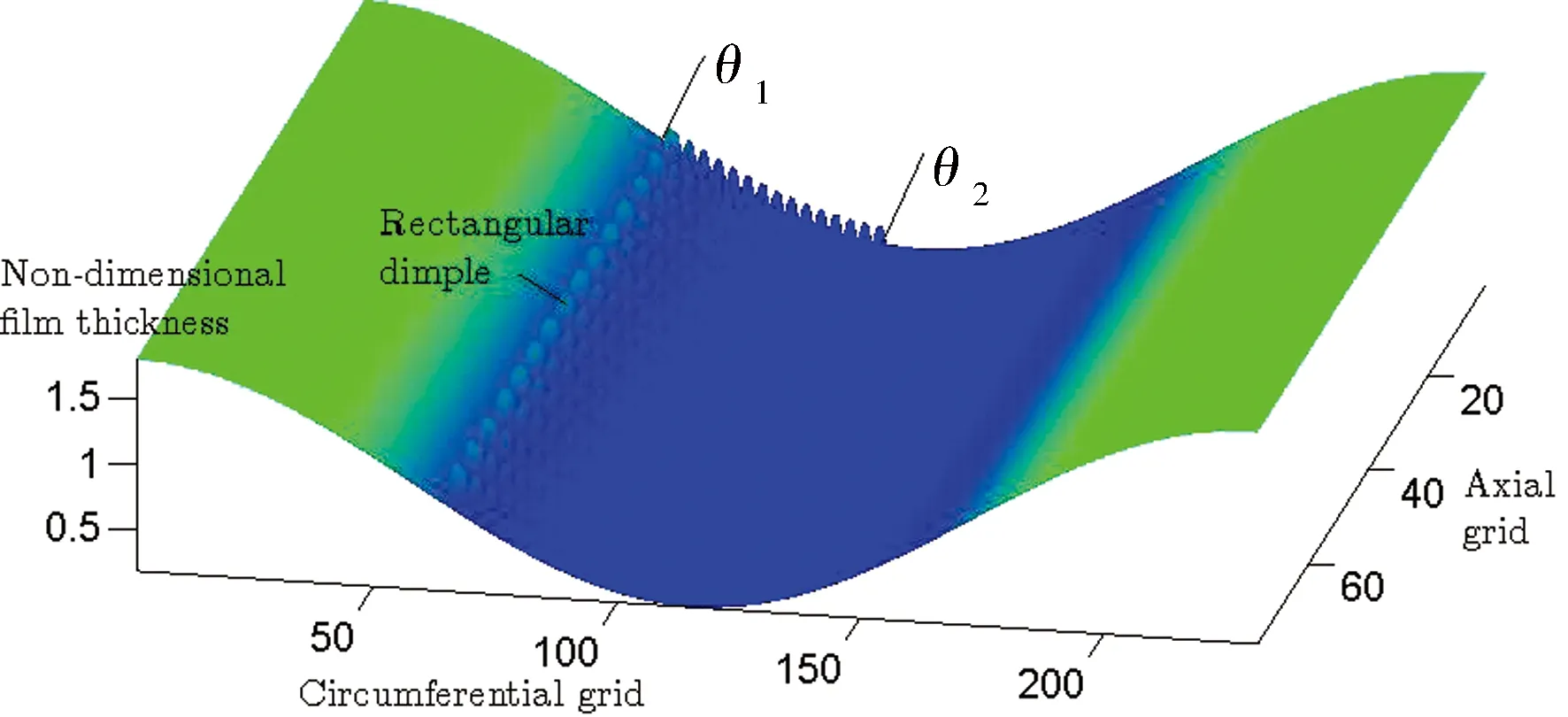
图3　织构分布的三维表示

1.2弹性变形方程

在Winkler弹性基础模型中，变形体被看成是一系列紧密排列的弹簧单元[20]。由于忽略相邻弹簧之间的剪切作用力，因此，轴承表面上某一点的实际弹性变形仅仅依赖于该点的接触压力、轴承材料以及轴承的几何参数。Winkler弹性基础模型描述的变形方程为

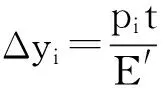
(5)

式中：Δyi表示某点处的弹性变形量，mm；t表示弹性层厚度，mm，本文即为轴承厚度；E′表示综合弹性模量[21]，在只有将单个接触体作为弹性体处理的情况下，可将其表示为

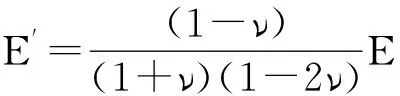
(6)

其中E和ν分别表示轴承的弹性模量和泊松比。图4示出无润滑和润滑条件下的Winkler弹性基础模型。需要注意的是：对于无润滑的轴与轴承直接接触的情况，Winkler模型中的压力为表面接触压力；在完全流体动力润滑的情况下，则为由式(1)计算所得的油膜压力。

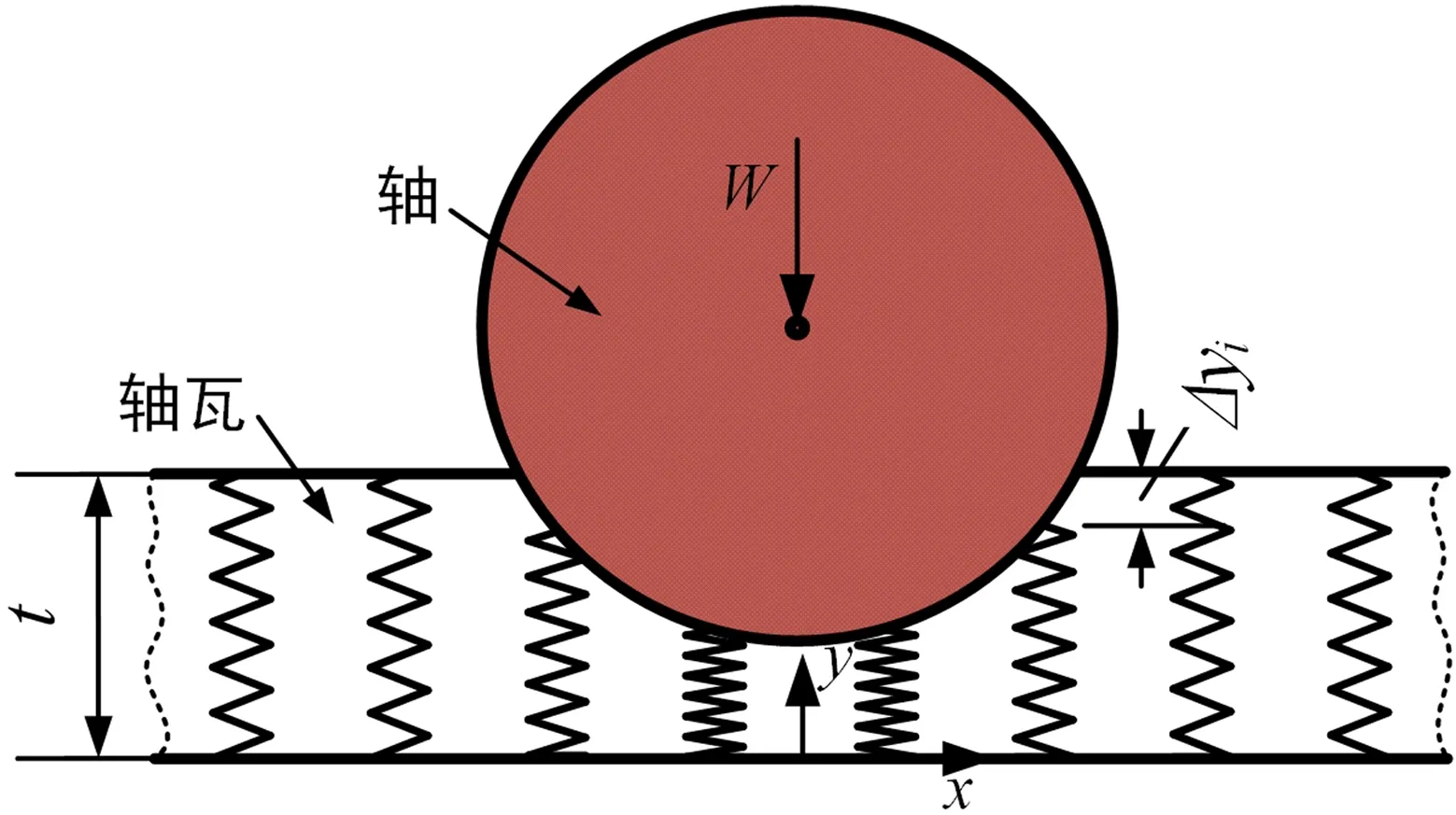
(a)无润滑

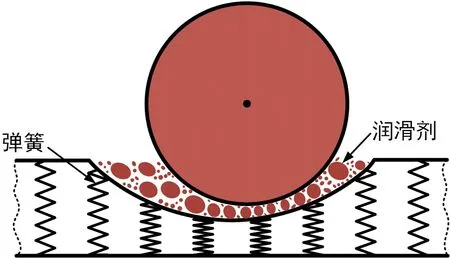
(b)润滑

1.3方程求解

本文使用最常见的有限差分法对Reynolds方程进行数值求解，分别用m和n表示圆周方向和轴向的网格数量，计算流程如图5所示。油膜压力可以通过检验如下的压力收敛条件而得到：

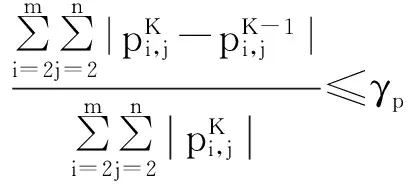
(7)

式中：K表示迭代次数；γp表示压力的收敛精度。

正如图4所示，恒定的载荷W/N被施加于轴颈中心并垂直向下，在开始数值迭代之前先分别给定偏位角和偏心率，等到压力和膜厚均达到各自的收敛精度之后，通过积分求出油膜合力F并进一步与外载荷W进行比较，若未达到预先设定精度，则改变偏心率继续迭代，直至满足收敛条件。另外，在分别计算油膜力在x和y方向的分量Fx和Fy时，通常油膜合力与载荷的方向偏差不能太大，该要求一般可表示为

|Fx/Fy|≤γ2。

(8)

如果式(8)不能被满足，说明起初假设的偏位角不够准确，一般需对其按照下式进行修改：

Φnew=Φold-arctan(Fx/Fy)。

(9)

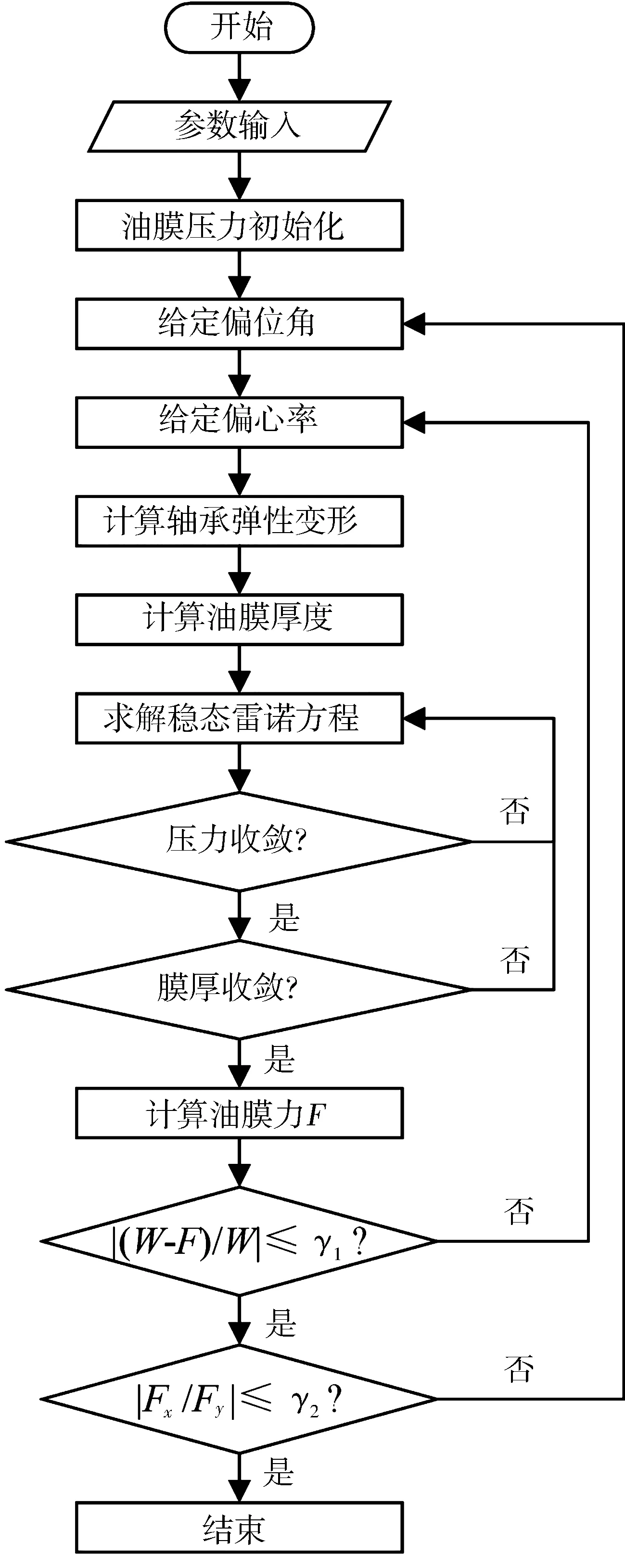
图5　计算流程

2计算结果与讨论

2.1网格无关性分析

通常情况下，数值计算时的网格质量对计算结果有重要影响，过少的网格可能会引起太大的计算误差，而过多的网格又会导致计算时间的极大耗费；因此，针对无织构轴承，进行了网格无关性分析。表1列出了不同网格数量和收敛精度下的轴承润滑性能计算结果。其中，H表示量纲一的油膜厚度(H=h/c)，d表示轴承表面的弹性变形，mm。可以看出，配置1与其他配置之间的差距比较明显，且随着计算精度的提高(配置4和配置6)，计算时间增加，计算结果却与低精度情况相差甚微(配置3和配置5)；因此，将配置3和配置5分别作为少量织构和多量织构情况下的网格配置。

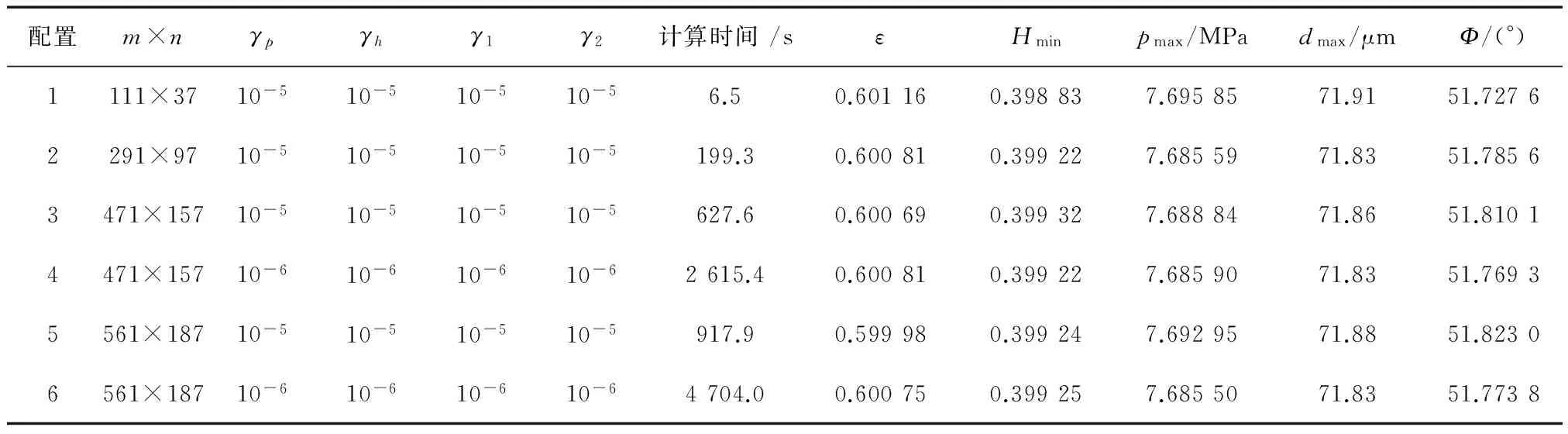
表1　各种网格和精度下的轴承润滑性能计算结果

注：γh为油膜厚度的计算精度；γ1为油膜力的计算精度。

2.2结果与讨论

选择如图6所示的长方体形微凹坑作为表面织构基本形状，轴承表面为可变形的、具有织构的静止面，轴颈表面为刚性且光滑的运动面。首先，分析在不同外载荷条件下轴承表面弹性变形对轴承润滑特性的影响，其结果如图7、8所示，计算参数如表2所示。从图7可以看出：在载荷不大的情况下，轴承表面弹性变形对油膜压力分布和膜厚的影响较小；当载荷增大时，变形对轴承性能的影响也相应增强。当外载荷W=5 kN时，刚性与柔性轴承最大油膜压力的绝对偏差为35.9 MPa，刚性轴承最大油膜压力的发生位置较靠前；当载荷增大到50 kN时，相应偏差已达到351 MPa，且可以较明显地观察到由变形引起的油膜压力“二次峰值”与膜厚的“颈缩”现象(图7(c)和(d))。由此可见，载荷对轴承性能具有重要的影响。

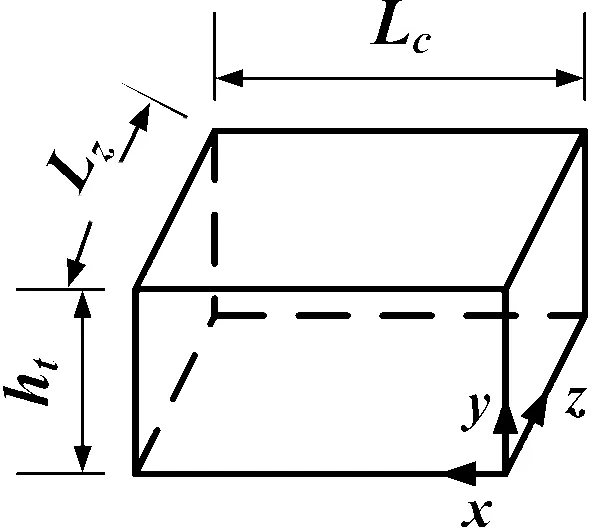
图6　单个长方体形微凹坑

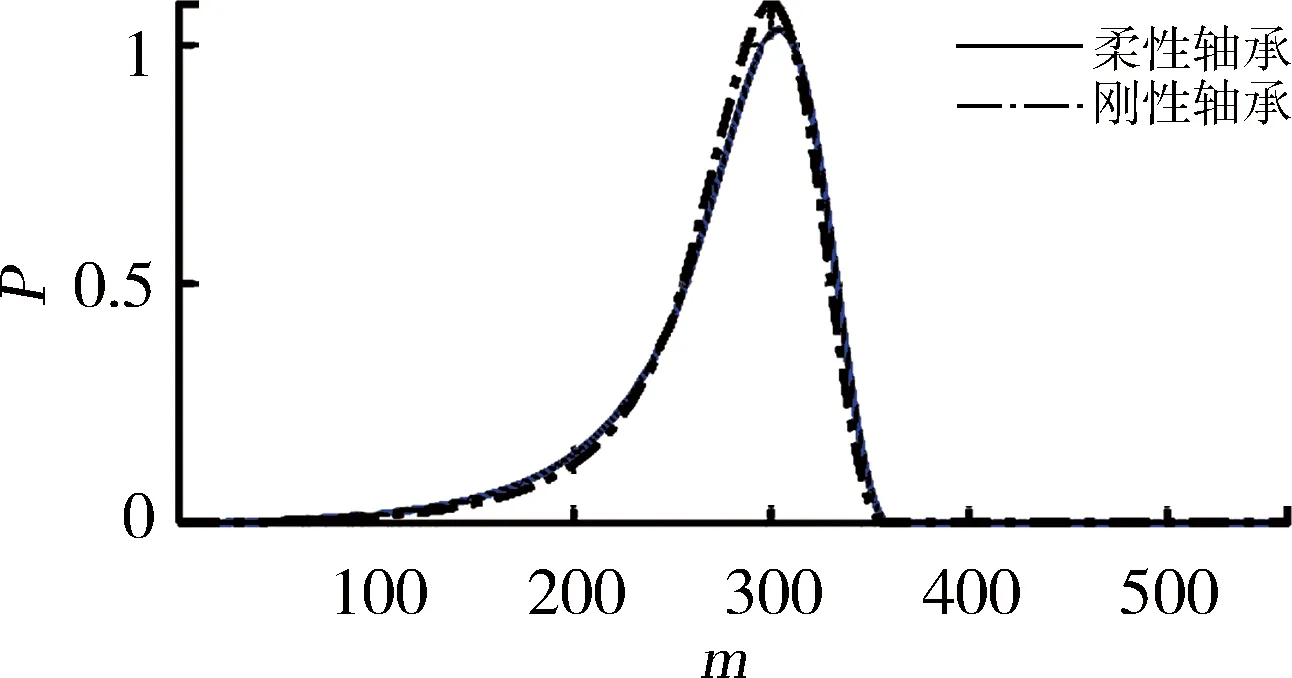
(a)W=5 kN的压力分布

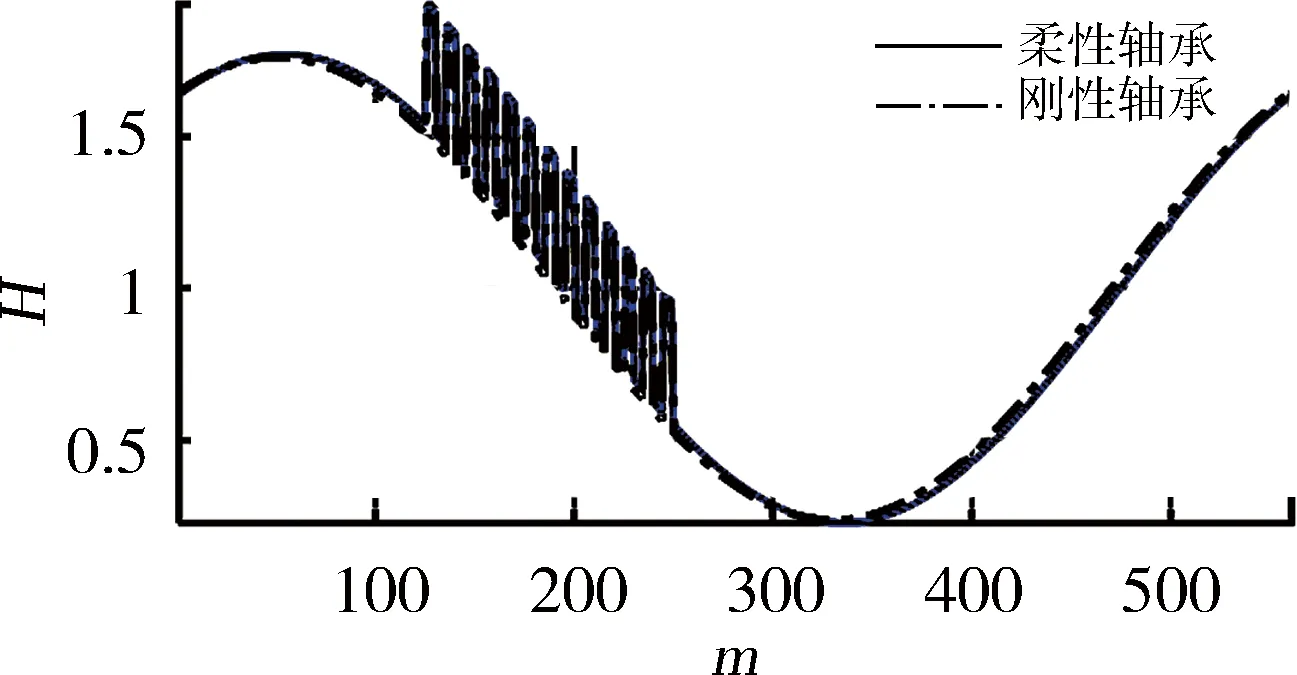
(b)W=5 kN的膜厚分布

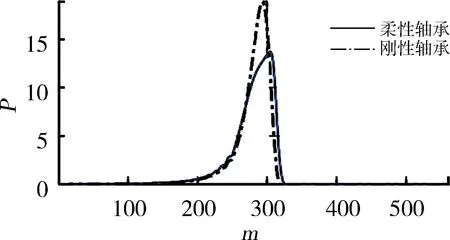
(c)W=50 kN的压力分布

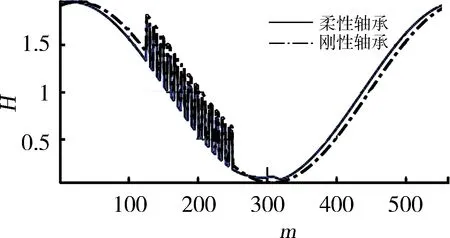
(d)W=50 kN的膜厚分布

图9示出21种织构配置对应的偏心率及偏位角与无织构情况的比较。其中，织构参数及其在轴承表面的分布位置见表3。从图9可以看出：仅仅有4种织构配置(Case 4、5、6和7)使轴承的偏心率降低，而大多数织构配置的偏心率均大于无织构轴承；Case 1、2和3的偏心率及偏位角几乎与无织构轴承相同；偏心率从Case8到Case17的变化幅度较小，最大的不超过2%(1.964%)，而从Case18开始直到Case21，偏心率迅速增大，偏位角也相应随之增大。

表2　计算参数 (Ht=ht/c)

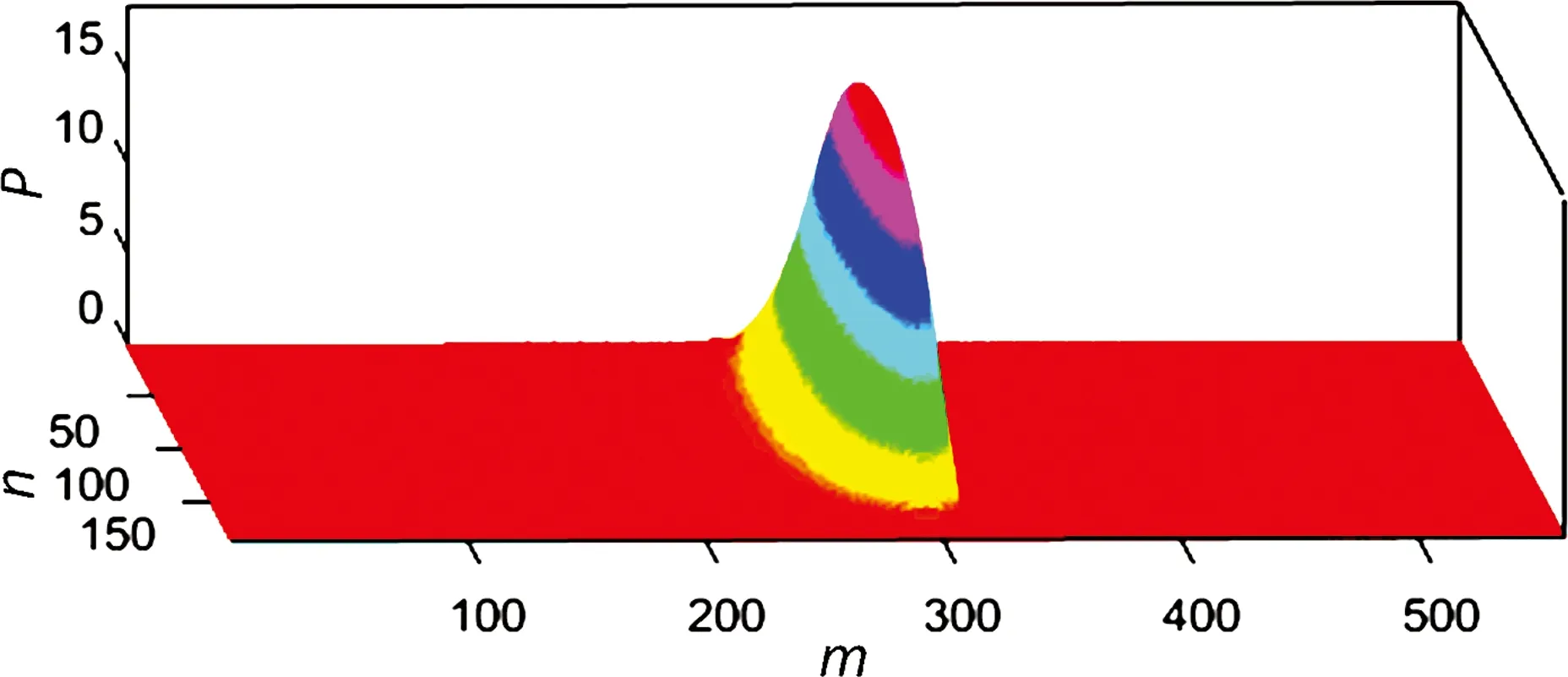
(a)刚性轴承压力分布

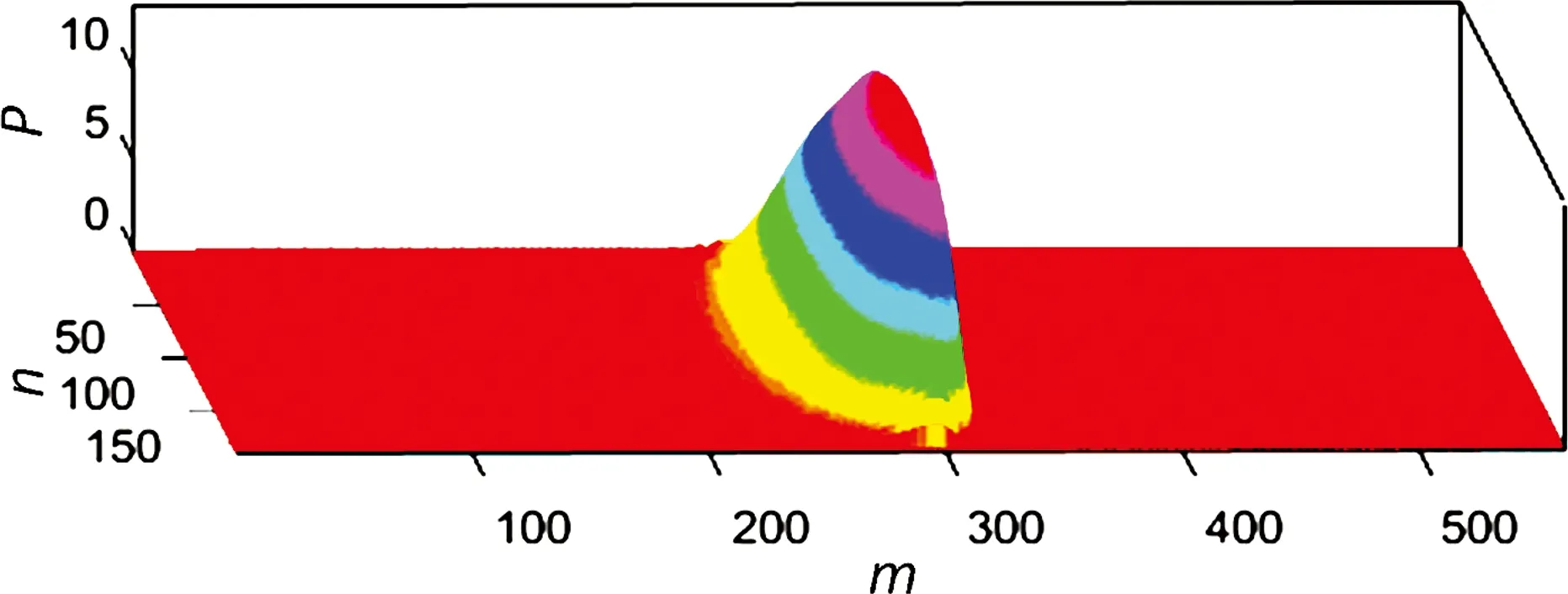
(b)柔性轴承压力分布

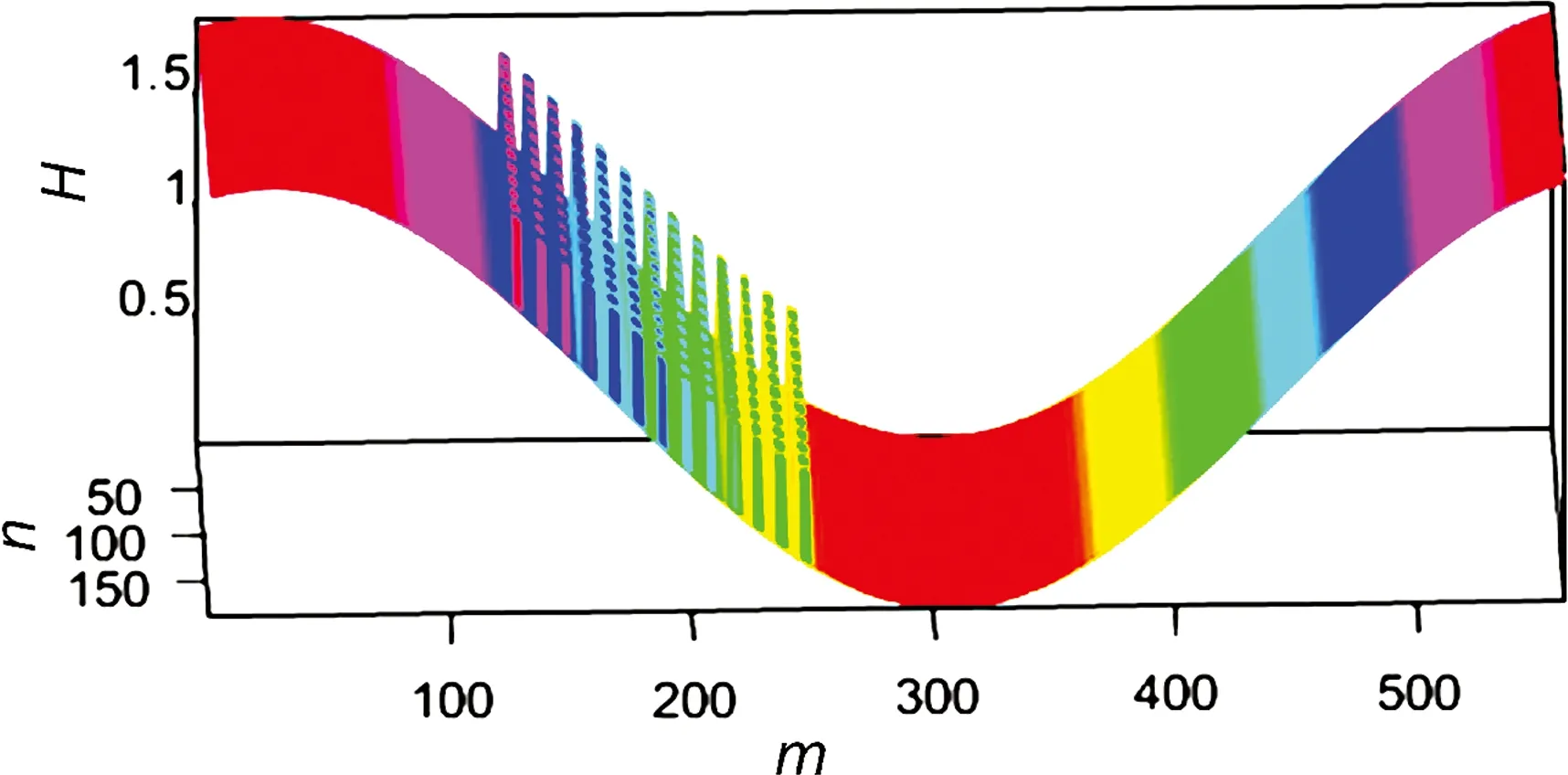
(c)刚性轴承油膜厚度分布

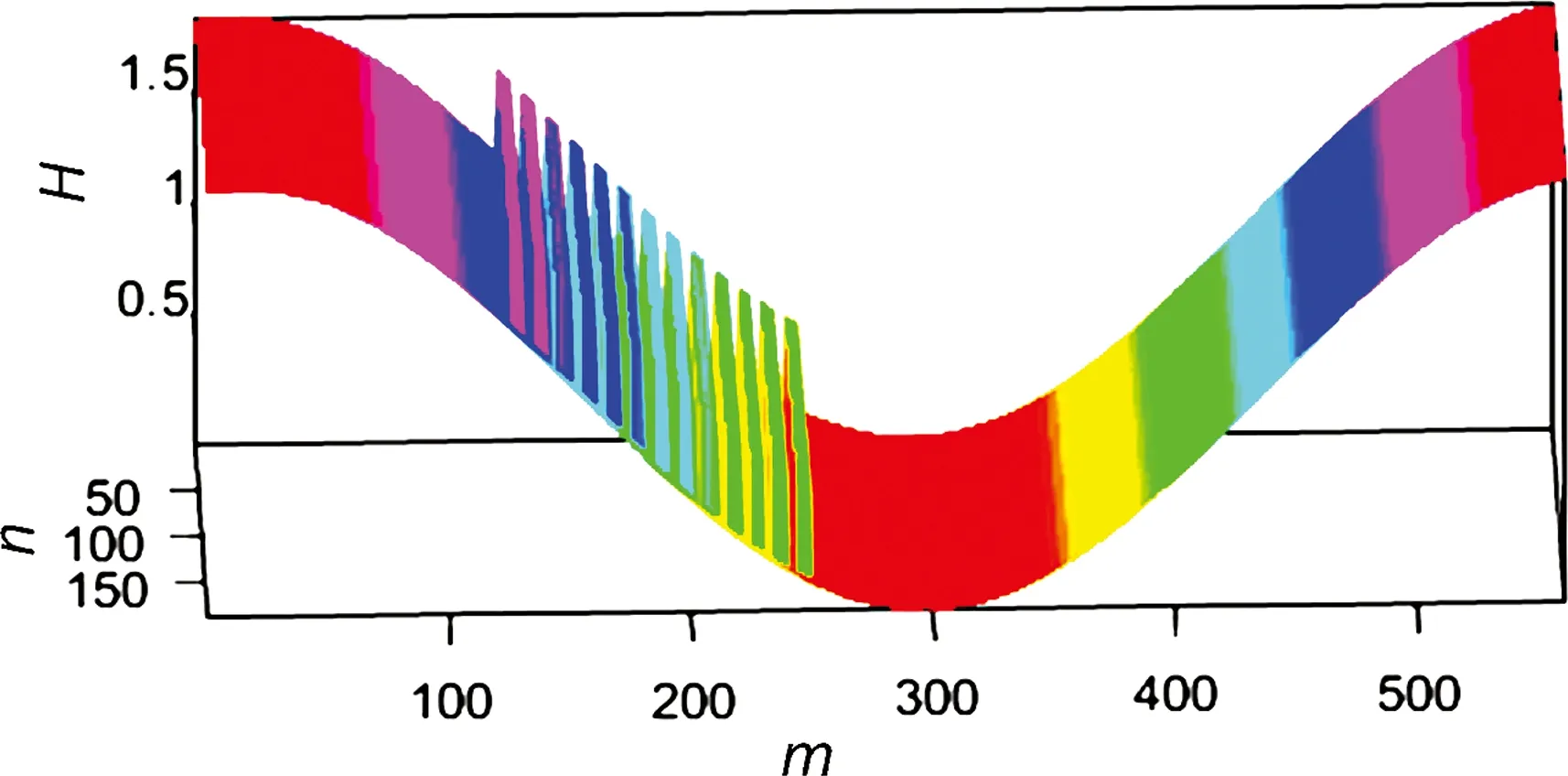
(d)柔性轴承油膜厚度分布

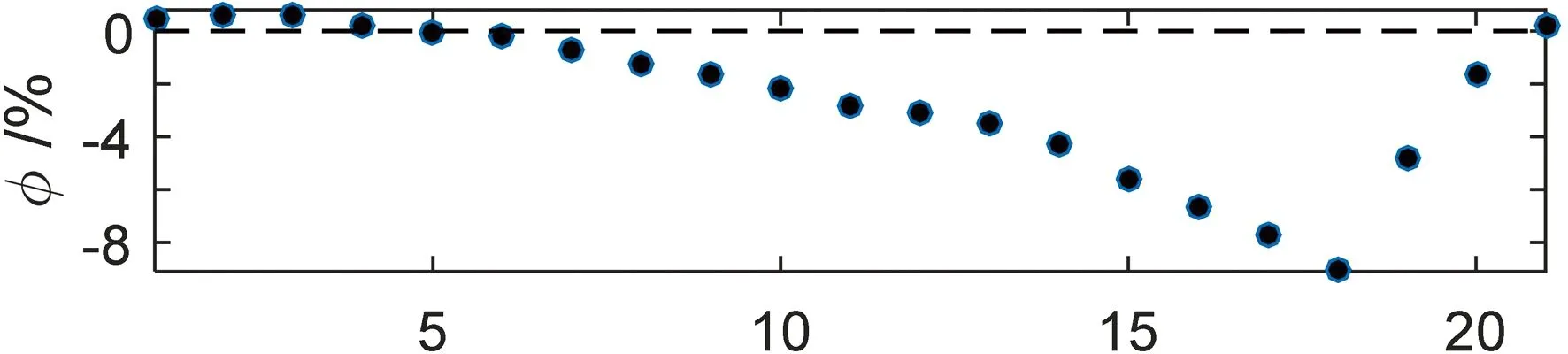
Case

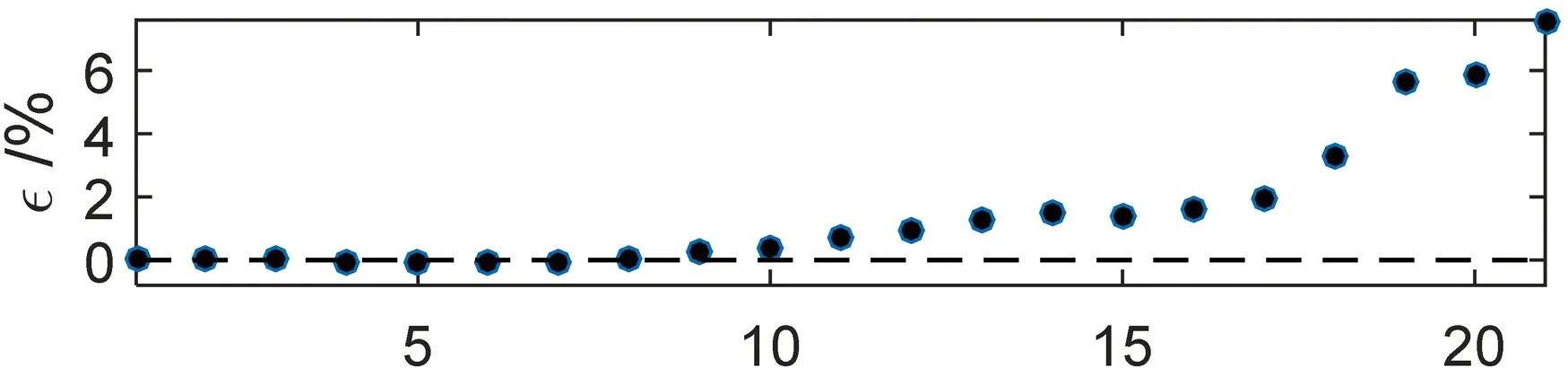
Case

Caseθ1～θ2(Nc=15,Nz=20,Ht=0.2,Lc/Lz=1)10～60210～70320～80430～90540～100650～110760～120870～130980～1401090～15011100～16012110～17013120～18014130～19015140～20016150～21017160～22018170～23019180～24020190～25021200～260

接下来研究织构在轴承表面分布位置及织构深度对油膜压力分布的影响。图10示出3种具有典型意义的织构在轴承表面的配置。其中，配置(a)的织构分布范围为105°～195°，配置(b)的织构分布范围为180°～220°，配置(c)的织构分布范围为205°～295°。可以看出，每种织构配置所产生的油膜压力分布是截然不同的：图(a)的最大压力发生位置与图(b)和(c)相比最靠后，大约在第320个网格节点处，最大量纲一压力值约为0.45；图(c)的最大压力位置最靠前，大约出现在第300个网格节点，其量纲一最大压力值约为0.254；图(b)的最大量纲一压力约为0.237，是三者之中最小的，但其中较大压力的持续范围是最广的，说明该区域压力的变化更加平缓；图(a)和(c)相对来说压力变化更为急剧，特别是图(a)中的压力较大的区域最窄小。

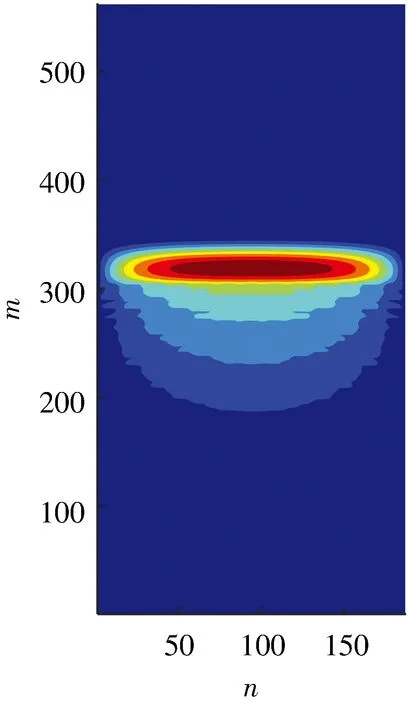
(a)在压力上升区域 (b)在最大压力区域两侧

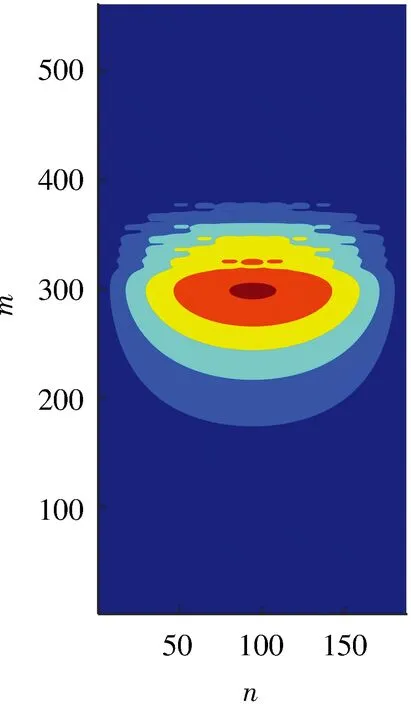
(c)在压力下降及空化区域

图11示出不同织构深度所对应的轴承横截面上压力分布情况，为能更加清楚显示出织构的影响，图中只截取了压力上升和下降部分，而没有对空化区域的压力进行展示(下同)。由图可见，织构深度越深，织构处的压力变化越显著，与分布在压力上升区域的织构相比，处于压力下降区的织构所引起的压力变化更为明显。

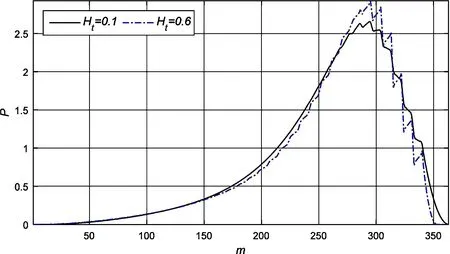
图11　不同织构深度的轴承横截面上压力分布

图12和13示出织构具有不同起始位置和不同终止位置形成的压力分布，其中每种情况的织构间距是相同的，而织构数量有所不同。图12的3种织构所产生的油膜压力局部存在微小差距，整体差别不显著。图13的3种情况之间的偏差非常明显，与上面所得到的结果相似，分布在压力上升区的织构在织构处引起的压力变化不如分布在压力下降区织构引起的变化显著，但却使压力峰值变大，且织构终止位置越靠近最大压力处，压力峰值越大。

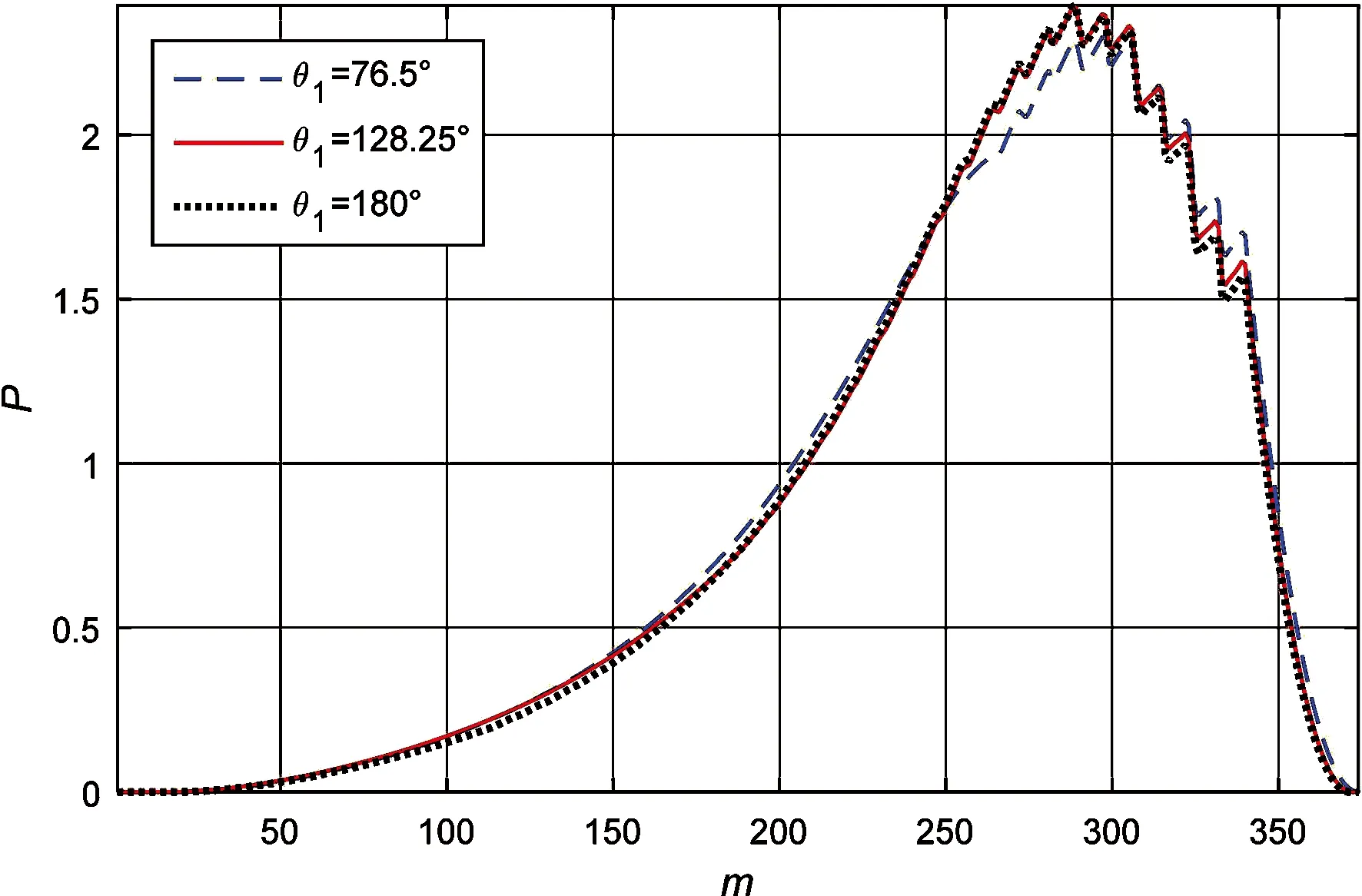
图12　织构起始位置不同所对应的压力分布(θ2=230°)

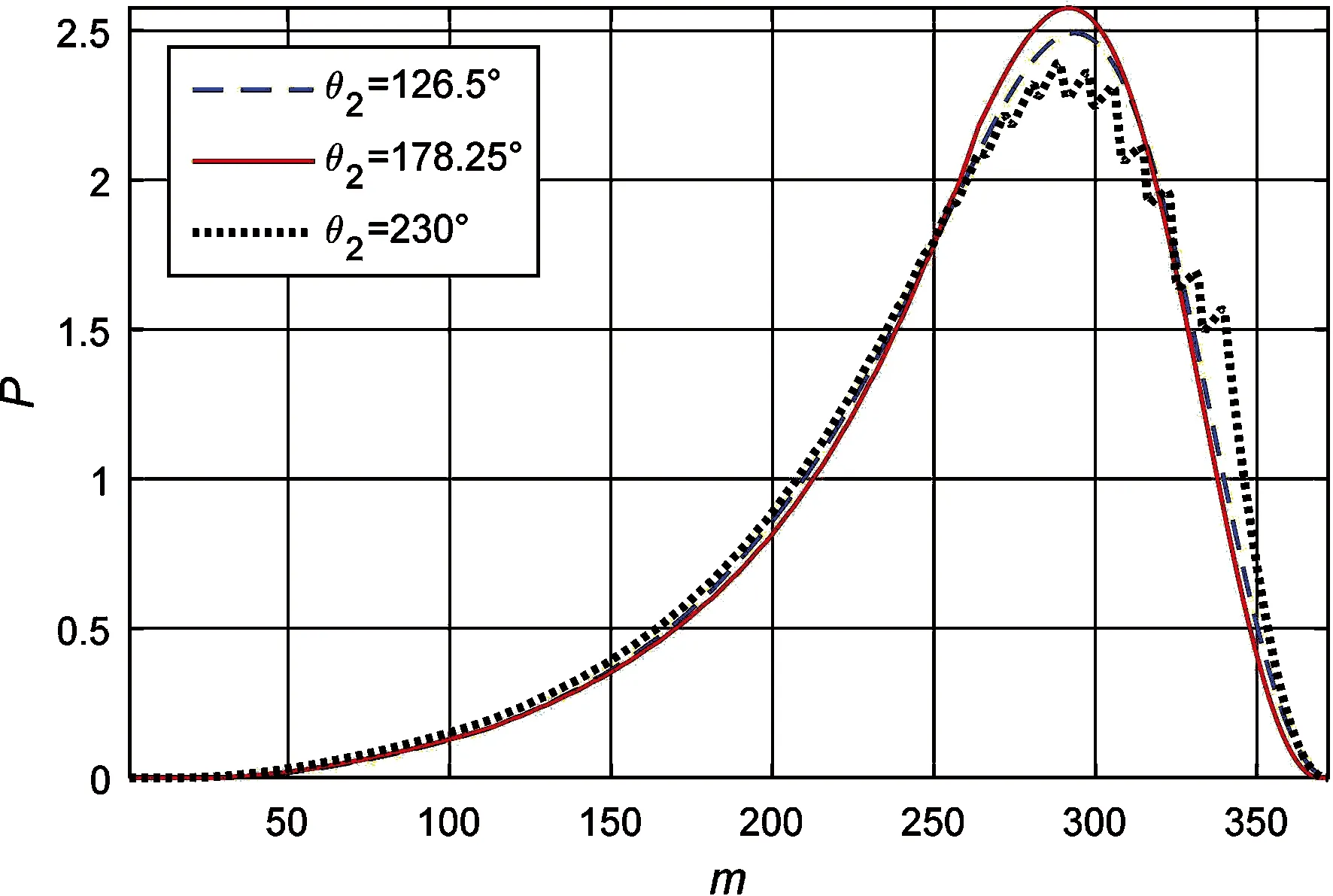
图13　织构终止位置不同所对应的压力分布(θ1=76.5°)

3结论

本文系统地研究了表面织构和弹性变形对径向滑动轴承性能的影响，分别考虑了不同载荷、不同织构分布范围以及不同织构深度的情形，其中，轴瓦被看作是弹性体，且在其表面分布有长方体形微凹坑群，轴颈假设为刚体且表面光滑，得到主要结论如下。

1)载荷对油膜压力分布和油膜厚度有重要的影响作用。根据Winkler弹性基础模型，载荷越大，其轴承变形也越大；因此，刚性和柔性轴承性能之间的差距越大，甚至当载荷非常大时，油膜压力会出现类似于反曲接触弹流润滑问题中的“二次峰值”现象，只是趋势并不非常明显。

2)织构的分布位置和范围对油膜压力及轴承性能亦有很大影响。分布在压力上升区的织构，虽然在织构处引起的压力变化不太显著，但是通常有助于改善轴承性能(降低偏心率)；分布在压力下降区的织构，尽管在织构处产生的压力变化比较明显，然而却并不能提升轴承的性能。另外，大的织构分布范围也并不一定对改善轴承性能有所帮助。

3)在一定的变化范围内，织构的深度越深，织构处的压力变化越明显，压力的峰值越大，在同样载荷下的轴承偏心率越大。

参考文献

[1]PETTERSSON U, JACOBSON S. Influence of Surface Texture on Boundary Lubricated Sliding Contacts[J]. Tribology International, 2003, 36(11): 857.

[2]马晨波, 朱华, 张文谦, 等. 往复条件下织构表面的摩擦学性能研究[J]. 摩擦学学报, 2011, 31(1): 50.

[3]张金煜, 孟永钢. 推力滑动轴承表面织构的优化设计[J]. 机械工程学报, 2012, 48(17): 91.

[4]YU H W, WANG X L, ZHOU F. Geometric Shape Effects of Surface Texture on the Generation of Hydrodynamic Pressure between Conformal Contacting Surfaces[J]. Tribology Letters, 2010, 37(2): 123.

[5]于如飞, 陈渭. 脂润滑条件下表面织构对滑动表面承载性能的影响[J]. 润滑与密封, 2014, 39(10): 1.

[6]FU Y H, JI J H, BI Q S. Hydrodynamic Lubrication of Conformal Contacting Surfaces with Parabolic Grooves[J]. Journal of Tribology, 2012, 134(1): 97.

[7]TALA-IGHIL N, MASPEYROT P, FILLON M, et al. Effects ofSurface Texture on Journal-bearing Characteristics under Steady-state Operating Conditions[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2007, 221(6): 623.

[8]YU R F, LI P, CHEN W. Study of Grease Lubricated Journal Bearing With Partial Surface Texture[J]. Industrial Lubrication and Tribology, 2016, 68(2): 149.

[9]TALA-IGHIL N, FILLON M, MASPEYROT P. Effect of Textured Area on the Performances of a Hydrodynamic Journal Bearing[J]. Tribology International, 2011, 44(3): 211.

[10]ETSION I. Modeling ofSurface Texturing in Hydrodynamic Lubrication[J]. Friction, 2013, 1(3): 195.

[11]姜亮, 马国亮, 王晓雷. PDMS表面织构润滑特性的研究[J]. 摩擦学学报, 2010, 30(3): 262.

[12]吴德龄, 马进. 弹性变形对滑动轴承工作性能的影响[J]. 北京工业大学学报, 1989, 15(4): 67.

[13]HILI M A, BOUAZIZ S, MAATAR M, et al. Hydrodynamic and Elastohydrodynamic Studies of a Cylindrical Journal Bearing[J]. Journal of Hydrodynamics Ser B, 2010, 22(2): 155.

[14]于如飞, 陈渭. 有限长轴颈轴承的弹性流体动力润滑分析[J]. 西华大学学报(自然科学版)，2016, 35(1): 13.

[15]岑少起, 陈瀚, 唐照民. 重载径向轴承润滑力学问题数值解[J]. 西安交通大学学报, 1982, 16(2): 119.

[16]黄平, 温诗铸. 多重网格法求解线接触弹流问题[J]. 清华大学学报(自然科学版), 1992, 32(5): 26.

[17]YANG P R, WEN S Z. A Generalized Reynolds Equation for Non-Newtonian Thermal Elastohydrodynamic Lubrication[J]. Journal of Tribology, 1990, 112(4): 631.

[18]LABOUFF G A, BOOKER J F. Dynamically Loaded Journal Bearings: a Finite Element Treatment for Rigid and Elastic Surfaces[J]. Journal of Tribology, 1985, 107(4): 505.

[19]CONWAY H D, LEE H C. The Analysis of the Lubrication of a Flexible Journal Bearing[J]. Journal of Tribology, 1975, 97(4): 599.

[21]BEI Yanhong, FREGLY B J. Multibody Dynamic Simulation of Knee Contact Mechanics[J]. Medical Engineering & Physics, 2004, 26(9): 777.

(编校：饶莉)

Study of Elastohydrodynamic Lubrication of Radial Bearing with Surface Texture

YU Rufei, CHEN Wei

(KeyLaboratoryofEducationMinistryforModernDesignandRotor-BearingSystem,Xi’anJiaotongUniversity,Xi’an710049China)

Abstract:In order to study the influence of surface texture and elastic deformation of bearing surface on the lubrication performances of radial bearing, Winkler elastic foundation model was used to calculate the deformation of bearing surface, and the finite difference method was employed to solve Reynolds equation. Finally, the bearing performances were computed and compared between textured case and untextured case under flexible and rigid conditions. The results of numerical simulation show that the surface texture has a more significant influence on the static characteristics of radial bearing compared with the bearing’s deformation. And the textures can significantly change the pressure distribution of oil film. Additionally, the location of textures on the bearing surface has different influences on the bearing performances. Generally, the textures located in the rising region of pressure have a positive influence on bearing performances, while the textures located in the declining region of pressure have a negative influence on bearing performances.

Keywords:surface texturing; radial bearing; elastohydrodynamic lubrication; Winkler elastic foundation model

收稿日期：2015-12-23

基金项目：国家自然科学基金项目(51175409)

中图分类号：TH117.2；TH133.3

文献标志码：A

文章编号：1673-159X(2016)03-0001-6

doi:10.3969/j.issn.1673-159X.2016.03.001

第一作者：于如飞(1987—)，男，博士生，主要研究方向为滑动轴承及流体力学分析。E-mail：yurufei@qq.com

·机电工程·