把随机性的数学直觉“概率化”——关于小学数学中“概率”教学的建议

◇张奠宙

把随机性的数学直觉“概率化”
——关于小学数学中“概率”教学的建议

◇张奠宙

新世纪以来，“统计与概率”单独作为一个学习领域列入小学数学课程，这是一次具有深远意义的里程碑式改革。但是，现行的小学数学教材里，只有“可能性”大小的讨论，没有给“可能性”赋以数值，更没有给出概率的概念。也就是说，直到小学阶段结束，连“概率”二字都没有在教材里出现。这样做，是否合适？值得研究。

《小学教学》杂志的主编殷现宾告诉笔者，本世纪初的小学数学教材里原来是有概率的。但是在教学实践中，出现了混淆理论概率和随机事件发生的频率（经验概率）的情形。因而在《义务教育数学课程标准（2011年版）》中就把小学数学中的概率去掉了。这是小学数学中名为“概率与统计”，学习领域里却没有“概率”的症结所在。

那么，新编的小学数学教材又是如何处理理论概率和经验概率之间的关系的呢？翻开某教材五年级上册，在摸棋子的几个案例中，虽然都默认每个棋子会被等可能地摸到，但是区别了两种不同的情形。

摸棋子活动：知道盒中红、蓝棋子各有多少（红4蓝1）。对于这一情形，本可以按照等可能性的理论探讨“可能性大小”，但教材（如图1）没有这样做，仍然借助摸20次，统计摸出红、蓝棋子的次数，得出的结果仅仅是“摸出红棋子的可能性大”。

摸球活动：不知红、黄球的数目。对于这一情形，无法使用“等可能性分析”，不得不根据160次摸球试验中随机事件发生的频率进行探讨 （如图2）。结果是摸出红球123次，黄球37次。由此得出结论：盒子里红球比较多。

图1

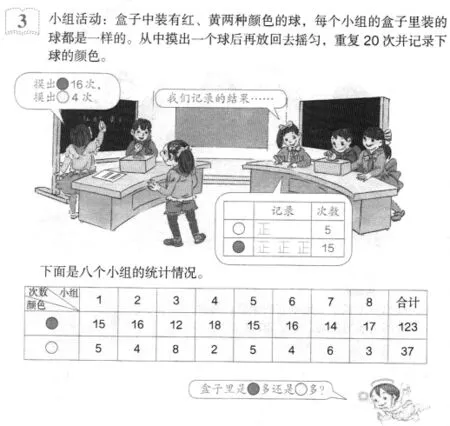
图2

仔细研读这两页教材，可以看到教材编写者的意图：对于可能性大小的判断，都不基于“等可能性”的理性判断，而是依靠小学生自己去摸，用经验性活动得来的频率来说事。甚至在摸棋子活动2结束后，竟要求全班学生每人掷一次硬币（如图3），企图让学生得出掷硬币正、反面出现的可能性差不多的结论。然而，掷几十次硬币，不但得不出应有的结论，反而会把思想搞乱。

图3

试问，在日常生活中，人们在作可能性大小判断时，所依据的究竟是等可能性的理性分析呢，还是靠大量的随机试验所得到的随机事件发生的频率呢？显然是前者。

事实上，等可能性分析是人类与生俱来的理性思维能力。

●在掷硬币活动中，正、反面朝上的可能性相同，世所公认。这无须投掷千万次来加以确认。

●在掷正方体骰子（质地均匀）活动中，1、2、3、4、5、6这6个面每个面朝上的可能性相同。这也无须通过大量的投掷试验来确认。

●在摸球（除颜色外，所有的球都相同）活动中，每个球被摸出的可能性都相同。盒中某颜色的球越多，该颜色的球被摸出的可能性越大。这也是凭直觉作出的判断，无须实际的摸球活动来确认。

●在转转盘（圆形）抽奖活动中，指针落在各个扇形上的可能性大小，取决于该扇形的面积占转盘面积的比例。

请大家想想看，这些判断是不是人们在生活中自然形成的？难道非要到学校学习才能学会？难道非要亲自掷硬币、掷骰子、摸球、转转盘很多次，靠得出的经验数据来验证一番，我们才会相信这些结论？事实上，大可不必啊！

由此可见，小学生的概率学习，应该建立在这些直觉的概率意识之上。这些理性分析，拿来用就是了，不必总是想着去“掷一掷”“摸一摸”。有人认为，现在强调小学生的操作活动、亲身体验、合作学习，所以要设计“掷”和“摸”的活动。然而，等可能性也是需要通过活动来加强认识的。如丢一枚纽扣能不能代替丢硬币？掷长方形的骰子每个面朝上是不是等可能的？摸球时为什么要搅匀？摸完后为什么要放回？这些都需要设计活动，从而使学生理解等可能性的意义。

值得注意的是，靠几个人掷硬币、掷骰子、摸球得来的数据，实在太少，不足为凭。将通过亲自试验得来的“频率”当成“概率”有其深刻而难懂的数学背景。例如：

●理论上，大数定律保证“频率趋向于概率”。至于什么意义下的趋向，有多种复杂的理解。小学阶段根本无法说清楚。

●实践中，大数定律要求做很多次实验，区区一个人、一个小组、一个班级的实验总数远远不够。

●频率是概率的近似值，不唯一，经常会变化，不好把握。

●对于频率与概率的关系，在高中阶段学习也很困难。因此不是年龄问题，而是因为它本身难理解。

由此可见，《义务教育数学课程标准（2011年版）》判定之前教学中出现的困难，在于硬是用少量“掷”和“摸”得来的各种“频率”，去取代由等可能性分析得出的唯一的“概率”。这是对“直觉概率”理念的一种干扰。由于没有大数定律的解说，小学生莫衷一是，出现理解上的困难。也就是说，教学中出现困难，不是因为给出“概率”才发生的，而是生吞活剥地滥用“频率”造成的。那种指望通过摸球和投掷行为就可以理解等可能性概率的意义的做法，不但无效，反而添乱。

这样一来，我们就不妨用新的思路，来确定小学数学中概率单元的教学途径：基于人类对等可能性的直觉认识，直观地引入概率，力求将直觉的随机性数学意识数量化。至于基于大数定律的“频率”，只能略微触及，适当提及，不能作为主线贯穿。

大家知道，概率论的教学是从随机变量开始的。小学数学也应如此。对于随机变量，要知道它可能取得的数值，以及取得这些数值的规律。至于如何描述这一规律，需要分成小学、中学、大学等多个层次，经过螺旋上升才能完成。

●小学水平。基于一些随机性生活体验，依据直觉理解概率的意义。可以考虑只给出离散型的古典概型的随机变量，它只有有限个等可能地取得的数值，可以给出取得每个数值的概率。也可以考虑给出简单的几何概型的随机变量。

●中学水平。随机变量的呈现，需要有分布函数的支持。借助大数定律理解概率与频率的关系。

●大学水平。基于概率的公理化定义，随机变量的呈现，要涉及基本空间、测度、可测函数、分布函数等知识。

这就是说，数学学习还是要回归数学本身。在小学阶段，必须直面“概率”概念，把随机性的数学直觉“概率化”。一般地，我们不妨把概率定义为：“用一个数来描述某种事件发生可能性的大小，称这个数为该事件发生的概率。”对五六年级的小学生来说，只要密切结合一系列的实例，依据直觉领会概率的意义，学习起来并不会感到困难。具体来说，我们建议在小学数学教材里安排如下的“随机性”数学基本活动。

一、掷硬币

“掷硬币朝上的面”是一个随机变量A（小学里可以不叫随机变量，只笼统地称为随机活动）。如国徽面朝上时令A取值1，币值面朝上时令A取值0，A取1和0的概率都是。我们建议用一个“概率表”表示该随机活动A。（如表1）

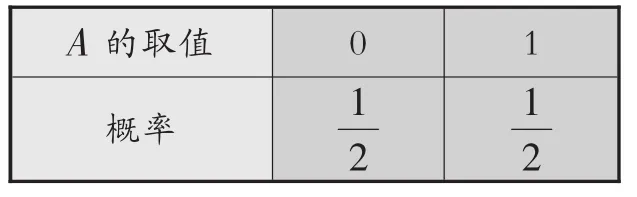
表1

二、转圆盘抽奖与几何概率

转圆盘抽奖，是社会上一种流行的随机性数学活动。圆盘上的指针可以随机地指向各个扇形。指向每个扇形的可能性大小（概率）由扇形本身面积的大小所决定。令整个圆盘的面积为1，于是，指针指向各个扇形的概率，就是等分后每个扇形所占圆盘面积的大小（其大小就是所对应的那个“分数”）。这是小学生非常熟悉的一种常识。

如图4中的圆盘，表面已经等分为12个不同颜色的扇形，每个扇形的面积都占，红色有4块，所以指针落在红色区域的概率是。同样，黄色和蓝色各有4块，则指针指向黄色和蓝色区域的概率也都是。可用表2记录。

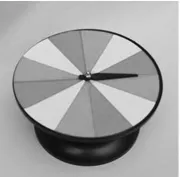
图4

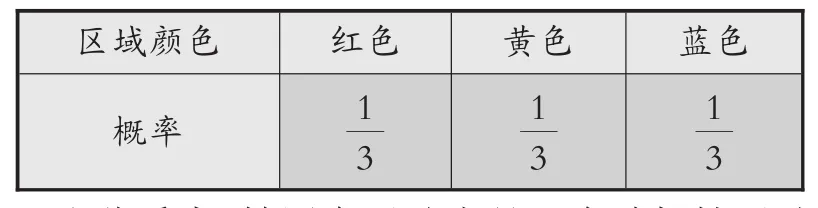
表2

由此看来，转圆盘活动也是一个随机性活动。该活动中所使用的几何概率，因其直观，且和分数定义非常相似（都基于面积的大小，以及将整个圆盘的面积定为1），因而最容易为儿童所接受。

三、掷骰子

掷骰子（质地均匀的正方体）也是小学生容易接触到的随机性活动。朝上的面的点数是一个随机变量，它的取值可为1、2、3、4、5、6。取这6个值中的每一个都等可能地发生，即发生的概率都是。我们可以用表3表示这种随机性活动。

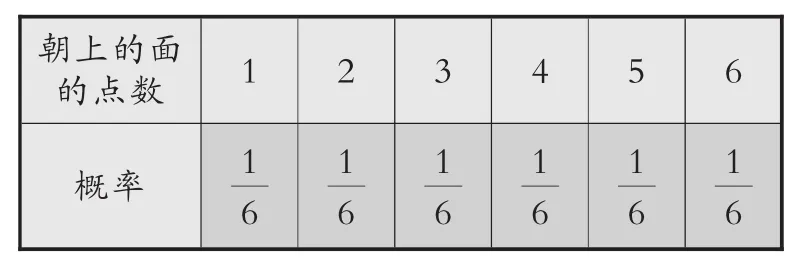
表3 掷正方体骰子时朝上的面出现某数的概率

四、摸球活动1

摸球抽奖是一种常见的随机性数学活动。在盒中放置若干个除颜色外其他都相同的球。摸哪种颜色的球出来是随机的。但是“摸出某种颜色的球”发生的概率，理应和该颜色的球数在总球数中所占的比例相同。例如，若盒中有4个球（黄3红1），因为黄球多，摸出黄球的概率就大；红球少，摸出红球的概率就小。具体来说，每次摸出黄球、红球的概率应该分别是，即黄球、红球在总体4个球中所占的比例。可用表4来表示。

表4 从盒中（黄3红1）摸球的概率

也就是说，由于事先已知盒中球的组成情形，可以通过直觉分析，按球数所占比例给出概率。

五、摸球活动2

反过来，现在如果只知道盒中有4个球（黄色或红色，除了颜色不同，其他都相同），但不知道盒中黄球与红球的确切数目，我们能不能从摸球活动中得出的数据，来猜想盒中黄球与红球的数目呢？这就相当于教材中的摸球活动。

通过160次摸球，我们得到表5。

表5

也就是说，我们可以从摸球活动中得出的经验数据，来大致确定经验性概率。

如前所述，如果盒中球是“红3黄1”，那么摸出红球和黄球的理论概率分别是，理论概率和频率可以比较接近，但二者毕竟是不同的。要使二者更加接近，就要大量增加摸棋子的次数。理论概率只有一个，而“频率（经验概率）”可以有无数个，不好把握。因此对于摸棋子这类可以进行理性分析的活动，尽可能采用理论概率。

六、射击运动员击中靶心的概率

射击运动具有随机性。每次射击受环境、心态、器械等的影响，不可能每次都击中靶心。那么，如何用概率描述某运动员击中靶心的可能性大小呢？事实上，对于射击这样的随机性活动，目前不可能理性地分析环境、心态、器械等因素，计算出唯一准确的理论概率。于是，不得不从经验数据来确定概率。

如果我们知道昨天某运动员的射击资料：在20次射击中，有16次击中靶心，那么我们就可以用“击中靶心”的频率，描述该运动员射击的随机性。

表6 某运动员射击时击中靶心的概率

也就是说，没有办法给出理论概率，只好用频率代替概率。这里仅仅是通过“昨天的20次射击”得出的频率。如果我们有更多的资料，就可以给出该运动员比较确切的频率值，即经验概率。

七、概率与决策：期望值

学习概率是为了指导实践。小学阶段，虽然由于学生知识广度和生活经验不足，不能正面提及概率的各种应用，但是，在常识范围内，还是可以有所作为的。数学期望，就是一个小学生可以接触的课题。

这就需要使用随机变量的数学期望概念加以论证，因而涉及分布函数及其积分，小学阶段根本无法处理。但是，如果诉诸“期望”一词的常识，混而不错地给出期望值的计算方法，最后形成决策，还是可行的。具体建议如下。

【数学期望值】

这样一来，如果你想快点得到奖金，那就去参加活动B，因为有一半的可能性会拿到钱，虽然只有100元。然而，从可以期望获得的奖金来考虑，当然参与活动A比较合算，中奖概率虽然只有，可是毕竟有1000元，可以派上大用场啊！

这样的解释，可以为小学生所接受，并为以后中学和大学的概率论学习打下一定的认知基础。培养学生的随机意识，在小学阶段形成概率教学的一个“直观性”的小循环，是一个不错的教学选择。

以上的讨论，是对课程标准的一些不同意见。正如新加坡李秉彝教授所说：“课程标准是家，不是牢房。”课程标准也是可以讨论的。孰是孰非，将由大量的教学实践来检验。

此外，某教材五年级上册“可能性”单元的后面，安排了一个“掷一掷”活动（如图5）。活动内容是掷两颗骰子得出两个数，将二者作和，得到结果A。数A的各种取值有不同的组合数目。如A取值5，可以有（1，4）、（2，3）、（3，2）、（4，1）共4组，详见表7。老师说：“我们来掷20次，如果和是5、6、7，8、9（的次数多）算我赢，否则算你们赢。”实践中，掷20次的结果，有13次A的值属于{5，6，7，8，9}，只有7次属于{2，3，4，10，11，12}，结论仅仅是老师赢的可能性大，仍然没有出现“概率”的字样。其实，这里已经在多处用到了等可能性的概念。例如，用表7计算一下便可知，老师赢的概率是（两颗骰子掷出的数字组合共36组，两数之和为5、6、7、8、9的组数之和为4+5+6+5+4=24），学生赢的概率则是。像这样用概率大小说明可能性大小，就更加科学、合理了。

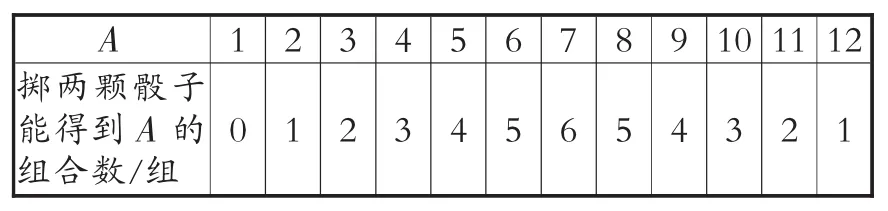
表7

图5

（作者系华东师范大学教授、博士生导师，《普通高中数学课程标准》研制组组长，本刊顾问）