对“认识乘法”教学盲点的思考

◇朱学尧

对“认识乘法”教学盲点的思考

◇朱学尧

在一次学校调研中，无意中翻阅了二年级第二单元“乘法口诀（一）”单元试卷。发现有这样一道题：“小明左手拿了6支铅笔，右手拿了5支铅笔，小明手里一共有几支铅笔？”我数了一下试卷，46个同学，居然有38个同学列成“5×6”。为什么学生学过了乘法算式，对用加法算式来解决的问题，却这样陌生？难道是认识“新朋友”，忘掉了“老朋友”？

一 倾听教师声音

经访谈，教师们一般认为：一是，学生刚刚学过乘法，认为正好可以用刚学过的乘法口诀，形成思维定式。二是，给的是文字题，没有图示，学生是不会分析数量关系的。更何况，在教学“认识乘法”和“乘法口诀（一）”时，教材中也没有出现列加法算式解决问题的题目；练习题中都是给图的，然后让学生看图列出算式，学生一般不会写错算式的。

二 审视教材单元内容的编排

教材在第一单元“认识乘法”中，提供了如下两个例题和一个练习。

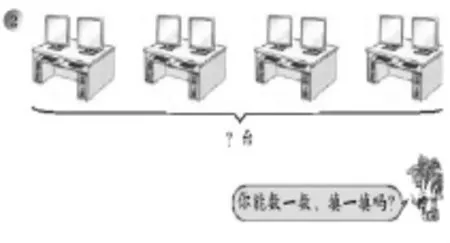
在例1教学中，主要目标是让学生结合情境图观察连加算式的特点，进而理解“几个相同加数相加的和是多少”可以说成“几个几相加是多少”。例2是让学生结合情境图来认识求几个几相加是多少，可以用一种新的算式来表示，进而引出乘法算式，以及乘法各部分名称和读法。而在相应的练习中，教材提供的素材的特点均是“一图两式”（加法算式和乘法算式），来让学生看图填写（改写）。例如：

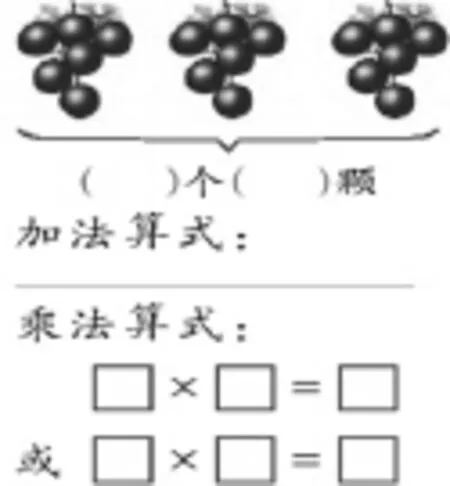
学生在做这样的题目时，几乎是不会出现问题的，因为学生通过直观图可以直接看出上面每串葡萄有6颗，有这样的3串，直接把“3”和“6”填在对应的括号里。这样顺利完成“大括号”下面的填写了。与此同时，学生也直接看出左边有6颗葡萄，中间有6颗，右边也有6颗，用加法算式自然是：6+6+6=18。学生在完成加法算式时，会这样想：加法算式中用到3个6，下面的乘法算式只要在3和6之间用“×”连接即可。同样，在第二单元“乘法口诀（一）”练习中，主要还是让学生结合情境图，学习1～6的乘法口诀，并列出乘法算式解决实际问题，复习第一单元对乘法的认知，在运用中巩固1～6的乘法口诀。

在这两个单元教学中，无论是例题还是练习题，教材提供的均是让学生“看图”“填空”。学生在完成上面几个填空时，思维缺少连贯性，没有从加法和乘法之间的联系以及乘法的意义上来整体考虑，也就是说看得多、说得少、想得少。这样，极不利于学生对乘法意义本身的理解。教学不能仅停留在算式的改写或填写上，学完这两个单元，至少还要让学生弄清解决什么样的求和问题只能用加法计算，解决什么样的求和问题既可以用加法也可以用乘法计算。如果处理不好这一问题，会直接影响后面单元“表内除法”的学习。我认为，要突破这一难点，在学生完成教材中图示题的填写后，教师还要有意识地引导学生连贯地说出图意。如，学生在完成上面“葡萄图”的填写后，可以引导学生说出这样的图意：“求一共有多少颗葡萄，可用算式6+6+6来表示。”这是基于学生已有的求几部分和的加法运算的经验。“三个加数都是6，还可用乘法算式6×3或3×6表示。”这是指向加法算式与乘法算式之间的联系点，或者说乘法算式是一种特殊加法算式的另一种表现形式。如果学生能够在看图填写算式时，在心里主动说上面两句话，那么，学生面对求和问题时，对于什么情况下只能用加法计算，什么时候可以用加法也可以用乘法计算，就有了深刻的认知，减少了思维定式的影响。

三 教学中需要加强的几个着力点

1.在情境中，构建加法算式与乘法算式之间的交融点。

在“认识乘法”单元里，为了提高学生对乘法的认知，沟通乘法和加法之间的联系，在解决问题时，教材提供的情境图均是把个数相等的物品连加在一起的。如，例1中兔和鸡，三个地方的兔均是2只，列式是2+2+2=6，四个地方的鸡均是3只，列式是3+3+3+3=12，以此来说明求“几个相同加数的和是多少”可以写成乘法算式。如果在第一、第二单元学生接触的都是这样的情境图，会给学生造成“最近我们学的都是求几个相同加数的和的问题，都可以用乘法来计算”这一片面的认知。笔者认为，在教学中，我们不妨在情境图中增添一些只能用一般的加法算式来解决问题的条件。如，在上面“鸡兔”情境图中，可以增加三个地方分别有2只鸭、3只鸭、4只鸭的情境。这样，列出的算式就是2+3+4。然后引导学生观察，同样是解决几部分和的问题，列出来的算式，有的几个加数是一样的，有的加数是不一样的，而唯有加数一样的情况下，才能用乘法这一新的算式来表示。这样可以让学生体会到，在解决问题中，求几个部分的和要用加法算式来表示，这是一般性的结论；同时，只有几个加数都相同时，才可以用特殊的乘法算式来表示，这就是数学中的一般与特殊之间的关系。这样，学生在解决问题时，就会有意识地分析几个部分量中的数据之间的特点，进而确定解决问题的方法。

2.在对比中，借助图式巩固乘法意义的生长点。

基于长期的教学目标，为了让学生更好地理解乘法的意义，培养学生分析问题和解决问题的能力。在看图填写算式的练习中，我们不妨加入一些只能用加法算式来计算的图题。

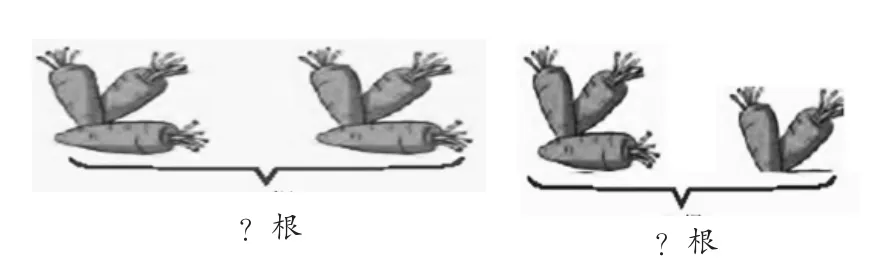
在解决问题之后，教师可提出这样的问题：第一幅图和第二幅图左右两边萝卜的个数有什么特点？解决的都是一共有多少个萝卜，为什么第一幅图可以用加法计算也可以用乘法计算，而第二幅图却只能用加法计算呢？这样，在交流中可以增强学生的辨析能力，使学生对乘法意义本质的理解更为深刻。

3.在串联中，找准图和文字之间过渡的衔接点。

教材中提供图，是让学生看图填写加法和乘法算式，是为了给学生提供初步认识和理解乘法意义的“拐杖”。但是，考虑到学生在一年级已经初步接触了一些简单的文字叙述题，笔者认为，在两个单元学习之后，需要在图和题的联系中，适时穿插一定量的文字叙述题，让学生摆脱“拐杖”，实现从“建立模型”到“解释运用”的过程。如，教学中不妨这样穿插文字叙述题：

（1）

（2）桌子上，左边有3个苹果，右边有3个苹果，一共有多少个苹果？

（3）桌子上，左边有3个苹果，右边有2个苹果，一共有多少个苹果？

然后提出这样的问题：“这三道题有什么相同点和不同点？”教师引导学生讨论，让学生明确：这三道题都是问“一共有多少个苹果的”，求“一共有多少个苹果”都需要把两部分合起来，即3+3=6，3+2=5。只不过，第1题与第2题，左右两边苹果的个数是一样多的，一个是用图表示的，一个是用文字叙述的，所以第1题和第2题还可用2×3来计算，第3题由于两个加数不一样，所以不能用2×3来计算。接下来再引导学生思考：在读图或读文字时，在确定是用加法还是用乘法计算时，首先要考虑的是什么？是不是所有求和的运算都可以用乘法算式来表示呢？你能在心中编一道用加法计算或乘法计算的题，说给同桌听一听，并用算式表示出来吗？如果学生真正经历了上面的图和文字叙述之间的转化过程，这对他们真正理解乘法算式的意义和作用，建构用乘法算式解决问题的模型是大有裨益的。

安徽蚌埠市禹会区教体局教研室）