聚焦思维发展：从算术思维走向代数思维——方程教学中的问题及启示

◇雍俊

聚焦思维发展：从算术思维走向代数思维
——方程教学中的问题及启示

◇雍俊

学生从四年级开始学习方程，这是学生由算术思维迈向代数思维的新起点。无论是用字母表示数，还是寻找数量间的等量关系，从认识方程到运用方程解决问题，对小学生而言都是很抽象的。那么，如何在教学中使学生学会用代数方法解决简单问题，并发展学生的代数思维呢？

一 代数思维与方程思想

由算术思维走向代数思维，思维对象和方式等发生着一系列的变化。

一是思维对象的改变。小学阶段学生初步的代数思维对象由原来的运算发展为对关系结构的思考，其中不仅包含计算，还包括对数量关系的分析。

二是思维方法的转变。代数思维方法是顺向思考与逆向思考的结合，将未知与已知同等对待，一同纳入问题的分析之中。

三是思维程序模式的改变。代数思维程序是先将等价的现象、数量关系进行描述，通过抽象进行数学化表达，进而解决问题。

史宁中教授曾说，方程思想的核心在于两点：一是模型思想；二是化归思想。学生学习方程的意义在于：一是学习在生活中从错综复杂的事情里，将最本质的东西抽象出来，这个过程是非常难的，也很有训练的价值；二是在运算中遵循最佳的途径,将复杂的问题简单化，这种优化思想对于学生的思维习惯的影响是深远的。

小学阶段一元一次方程教学的重点是让学生学会分析已知量与未知量的关系，从信息中建立等量关系，并用数学符号进行表达。在从算术思维走向代数思维的过程中，方程所起到的作用在小学阶段是非常重要的。

二 儿童学习中常见的问题

1.对方程有无优势的理解不同。

方程方法与算术方法是否存在孰优孰劣的问题？大家观点不同，一种观点认为方程方法是代数思维，研究对象和思维方式都较抽象，方程方法优于算术方法；另一种观点认为，方程只需要将相等的数量关系用数学符号表达出来，利用方程解决问题的思维含量并不见得比算术方法多。相比上述两种观点，认为方程是打开学生解决问题的另一扇门的观点更容易让人接受，这种观点认为，方程方法和算术方法都是学生解决问题过程中的一种思维方式，供学生解决问题时选择。

四年级学生在学习“认识方程”内容时，兴趣还是比较高的。然而，在解决问题时却并不一定喜欢用方程解决。原因主要是与算术方法相比，用方程解决问题稍显烦琐，有学生甚至直言不讳地说 “用方程要写好多字，麻烦”。但五六年级的学生在逐渐适应了方程的思维方式后，明显倾向于用方程解决问题，特别是在解决一些包含复杂数量关系的、逆向思考的问题时，用方程解决要简单得多。

我们认为，学生对方程的喜好程度不同，决定了在各年级教学的重点应有所不同。

2.思维建模困难，难以从信息中提取等量关系。

受思维习惯和对数量关系分析能力的影响，学生在描述两个等价事物之间的关系时，会出现较大的困难，难以描述或找出问题中蕴含的等量关系。而用方程解决问题的关键是找出等量关系，如果这一步学不好，将直接影响他们以后学习列方程解决问题。

从思维发展的角度来看，学生的思维正处于由具体形象思维向抽象思维过渡的阶段。因此，将思维对象从具体的数值计算转移到抽象的数量关系上，将未知数与已知数一起放入算式中参与运算这一思维方式还未形成，需要逐步适应。

3.数学抽象表达不严谨，等量关系与方程不对应。

在用方程解决问题时，先让学生用自然语言阐述要解决的问题，然后抽象成数学语言，最后用数学符号建立方程并解决问题，这正是建模的全过程。而在抽象成数学语言时，很容易出现与自然语言表达不相符的情况，信息与问题描述较混乱。

找出等量关系后怎么用，这是学生经常面临的问题。在解决问题的过程中，很多学生往往会因为题目中要求写出等量关系而去找等量关系，但在列方程时又根据思维习惯写出与其不匹配的方程。较常见的是四年级学生经常会列出形如“x=_”的式子，或者与等量关系不一样的方程，如根据“部分量+部分量=总量”写出等量关系，但在列方程时用的是“总量-部分量=部分量”等。

4.列方程易，解方程难。

小学阶段解方程的方法，主要运用等式性质，或根据四则运算各部分之间的关系解方程。然而，在学习过程中，学生容易列出未知数为减数或除数的方程，从而给解方程造成困难。另外，有些老师为体现方程的优越性，在四年级进行两种方法的对比练习时，以复杂的问题为背景，如小明登山，上山的速度是 2千米/时，下山的速度是3千米/时，共用4小时，问上山的路程为多少千米。学生很容易设上山的路程为x千米，进而列出方程x÷2+x÷3=4，却不会解。这也是困扰教师教学的一个重要方面。

三 儿童思维发展走向对教学的启示

1.聚焦思维对象，重视寻找等量关系。

分析数量关系是列方程解决问题的关键，着力培养学生寻找等量关系的能力是教学的重点。

北师大版教材四年级下册“认识方程”单元中特意安排了“等量关系”一课，给出了等量关系的名称，并对如何找等量关系进行讨论，使学生知道等量关系在日常生活中的广泛存在。这样编排突出了核心知识的作用和价值。

如何凸显等量关系的重要性，为学生后续的学习打下良好的基础呢？建议教师们在“认识方程”单元的教学结束时，系统总结寻找等量关系的方法，因为方法的明晰有助于学生在分析问题时灵活选择。可以从以下几个方面着手：

①直接根据四则运算的意义分析数量间的相等关系。

②根据常见的数量关系寻找等量关系。

③根据常用的公式找出等量关系。

④根据表示数量关系的关键语句寻找等量关系。

在用方程解决问题的练习中，可以选取以下素材进行找等量关系方法的梳理总结。

①爸爸今年33岁，比小明年龄的3倍还多6岁，小明今年多少岁？（四则运算意义）

②长方形的长是12厘米，周长是34厘米，宽是多少？（常用公式）

③一列火车出发后经过A站时下了38人，上了135人；经过B站时下了57人，上了18人，到终点站时共498人下车。出发时列车上有多少人。（事件发展顺序）

2.重视用不同形式表示数量关系。

培养学生分析问题、解决问题的能力，可以从多方面入手，如根据信息写出等量关系，或根据等量关系画出示意图、线段图。北师大版教材五年级下册第七单元 “用方程解决问题”中出现了要求先将题目中的等量关系表示出来，再列方程解决问题。如在“邮票张数”一课中（如下图），要求首先找出题中的等量关系，并进行表示。教材上呈现了学生的不同思路，既有数学表达式的运用，也有直观图的呈现，这对学生分析数量关系很有帮助。

实际上，运用直观图不仅能帮助学生清楚地分析数量关系，还有助于学生把复杂的数学问题变得简明、形象，也有助于探索解决问题的思路。

3.逐步改变学生的思维方式。

算术方法重在让学生用已知去表达未知，分析数量关系时可从问题入手，或从条件入手；而方程是把相等的两个量或事物表示出来，其中已知和未知均按照相应的关系表达出来，都要参与其中。在方程的教学中，“不要过于强调已知、未知，而要强调用数学符号把要说的话（即两件事情等价）表达出来。这个是根本，是学生必须真正掌握的东西”，这就决定了学生的思维方式必定要发生改变。

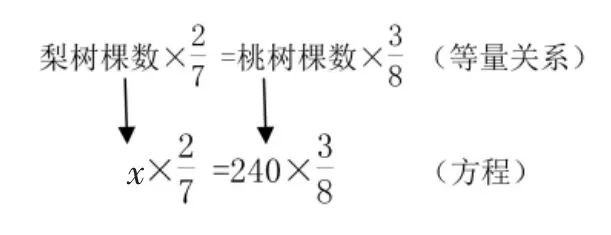
教学中需要突破以下几点：一是要让学生理解未知数为什么会参与列式和运算；二是未知数参与运算与以往算术方法的区别是什么；三是如何让学生习惯用方程解决问题。可以借助具体的问题，引导学生找出数量之间的关系，构建等量关系，列出方程，从而解决问题。如，果园里有桃树240棵，梨树棵数的和桃树棵数的一样多，梨树有多少棵？先分析关键句，找出等量关系，而后对照等量关系，列出方程并解决问题，如下图所示。

4.遵循思维发展规律，使学生逐步适应代数思维。

北师大版教材共安排了四次对式与方程的学习。第一次在四年级下册，主要内容是初步认识方程，会用等式的性质解简单的方程，会列方程解决简单的实际问题；第二次在五年级下册“分数除法”中，安排了运用方程解决简单的分数问题；第三次在五年级下册 “用方程解决问题”单元，主要内容是解形如2x-x= 3的简单方程，进一步运用方程解决问题；第四次在六年级上册，会用方程解决稍复杂的分数、百分数问题。

从教材的安排来看，重视了学生学习方程的循序渐进性，体现了知识形成的过程，遵从了学生从算术思维走向代数思维的发展方向。

教学中，遵循学生的认知特点和思维发展规律教学方程，相信能达到事半功倍的效果。

[1]史宁中，孔凡哲.方程思想及其课程教学设计[J].课程·教材·教法，2004（9）.

[2]汪绳祖.小学数学教育学[M].北京：高等教育出版社，1997.

四川大学附属实验小学分校）