地震条件下桥台主动土压力的合理简化计算方法

刘　坤，陈幼佳，2，章　敏

(1.太原理工大学 建筑与土木工程学院，太原 030024；2.美国宾夕法尼亚州立大学 土木工程学院，米德尔顿 PA 17057)



地震条件下桥台主动土压力的合理简化计算方法

刘坤1，陈幼佳1，2，章敏1

(1.太原理工大学 建筑与土木工程学院，太原 030024；2.美国宾夕法尼亚州立大学 土木工程学院，米德尔顿 PA 17057)

摘要:在库伦土压力的基础上,结合桥台实际结构形式,推导地震条件下桥台主动土压力计算方法，并将该计算方法与传统的库伦土压力理论、M-O法土压力理论以及近期林宇亮计算方法进行对比分析,同时分析了该计算方法中参数影响变化规律。分析结果表明，传统计算方法得到的土压力值相对较低,本计算方法可使桥台土压力计算值增大10%～40%,结果更趋于安全;本计算方法参数变化影响与传统方法相一致，及填土内摩擦角越大,台背倾角越大,桥台土压力越小。

关键词:地震;桥台;土压力;土楔形体平衡理论;土体倾斜破坏角

近些年,地震频发,作为交通咽喉的桥梁结构如何保持良好的作用显得尤为重要。大量地震灾害研究资料表明,桥台在地震作用下由于土压力过大而破坏,进而引起桥梁倒塌导致交通瘫痪的情况十分常见[1]。地震条件下桥台主动土压力的大小和分布也是桥梁工程以及岩土工程等领域的一个非常重要且紧迫的问题[2-4]。关于地震条件下桥台主动土压力计算,我国一直采用的是拟静力计算方法中的Mononobe-Okabe计算方法(M-O法),然而M-O法适用范围非常有限。MYLONAKIS et al[5]曾对其进行补充和发展,但是仍未考虑到桥台的自重和刚度都较大、还受到上部结构和基础的约束等特点。用上述方法计算地震作用下桥台土压力并不准确而且安全系数不高。

在库伦土压力计算理论[6]中并未具体给出临界破裂角θ的值,只是提到使土压力值F取得最大值时的θ值,用微分方法使得dF/dθ=0得出θ的取值,从而得到F的最大值。利用微分方法求θ的值,过程十分繁琐,对数学计算能力要求较高,对此林宇亮提出利用图解法求解θ的值[7],并得出黏性土条件下土压力的计算方法,然而其计算过程也存在部分误差,在此笔者改进了林宇亮的图解法,使之更符合真实条件。

李涛[8]针对铁路桥台,忽略竖向地震作用,只考虑水平地震系数得出了地震土压力计算公式,避免了M-O法中地震角的概念。梁波[9]根据桥台的实际情况:台背倾角较大时,如按照原来的计算公式可能产生较大误差的基础上,提出了计算桥台地震土压力的简化公式,突破了M-O法在计算填土水平、内摩擦角小于地震角时无法计算的局限。还有很多专家学者对于土压力分布、有限元软件模拟以及模型试验等方面进行了大量研究[10-14]。

针对前文大量关于挡土墙土压力的研究,笔者考虑桥台的实际情况后,在梁波土压力分析方法基础上,对土楔形体进行受力分析,计算地震下桥台主动土压力值,并采用图解法分析土楔形体倾斜破裂角的大小,克服了林宇亮在求解过程中的不足,得到桥台台背土楔形体,倾斜破裂角极值的表达式,进而得到地震条件下桥台主动土压力极值的表达式。

1土楔形体的受力分析

图1为某桥台以及填土的断面图,台背与水平面的夹角为α,在计算过程中沿桥台顶点A做竖直线将台背填土分成两部分,一部分为桥台下部填土,另一部分为桥台背后填土。桥台高为H,桥台与土的摩擦角为δ,土内摩擦角为φ,重度为γ。计算AB面土压力,先计算三角形土体ACD作用在AC面的土压力,再计算三角形土体ABC在地震作用下的惯性力,二者叠加即为AB面土压力。

图1　桥台与填土断面Fig.1　Cross section of abutment and backfill

1.1土楔形体ACD受力分析

土楔形体ACD受力图如图2所示,其受力主要有:自身重力G1水平地震加速度以及竖向地震加速度引起的惯性力khG1和kvG1；CD面下土体对于土体ACD的反力F,以及在AC面处由土体ABC传来的反力Fa1,由于是土体内部之间的相互作用,Fa1和F的偏角均为土内摩擦角φ。

图2　土楔形体ACD受力图Fig.2　Force analysis of soil wedge ACD

由受力平衡分别建立x向和y向平衡方程:

由x方向平衡条件得:

(1)

由y方向平衡条件得:

(2)

联立(1)和(2)解得

(3)

式中：

在式(3)中除θ外,其他参数均为已知,或可从设计图中推算得到。

在库伦土压力理论中关于θ的定义为:在所有可能的破裂面倾角θ中,存在一个使得主动土压力Fa为最大值的破裂面倾角θcr。欲求θcr使Fa达到最大值,只需令dFa/dθ=0即可,但这样计算极为复杂,对数学能力要求较高,而且得不到显式的结果。林宇亮提出用图解法对θ作简单变换,根据三角形的基本知识推导出θcr的值,并得出Fa的最大值即所求的主动土压力。利用图解法求解的过程如图3所示,具体步骤如下:过C点作直线CN与水平方向的夹角为φ,且与AD延长线交于F点；过A点做直线AM,使之与AC交2φ角；过D点作DN,满足AM//DN。那么,AC，CM，AM，CF，AF，FM的长度均为常量,只要φ角确定,这些线的长度都可以确定。

最终通过三角形相似以及基本三角形定理可得出:

(4)

(5)

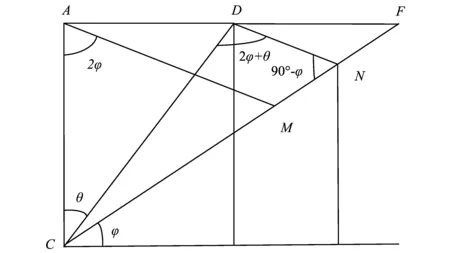
图3　图解法求解图Fig.3　Graphic method for solving

1.2土楔形体ABC受力分析

土楔形体ABC受力如图4所示,其受力主要有:自身重力G,水平地震加速度以及竖向地震加速度引起的惯性力khG和kvG；AC面土体ACD的土压力Fa1,以及在AB面处由桥台传来的反力Fa。此时，AB面为桥台和土的接触面,所以Fa偏转的角度为桥台与土之间的摩擦角δ。

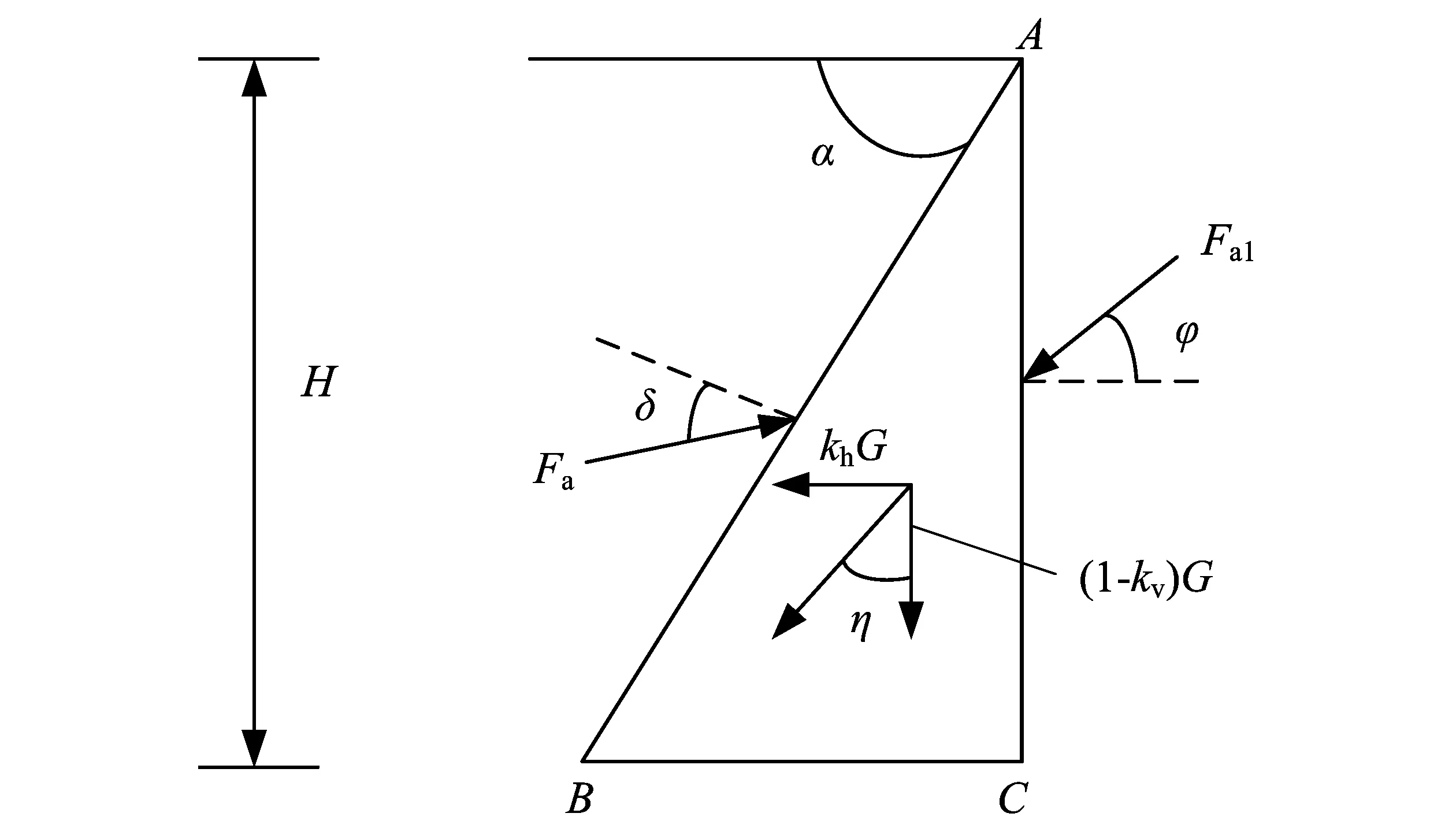
图4　土楔形体ABC受力图Fig.4　Force analysis of soil wedge ACD

由于Fa1为已知,且

(6)

建立x方向的平衡方程可得:

(7)

解得

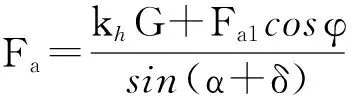
(8)

将式(5)和式(8)代入可得:

(9)

式中

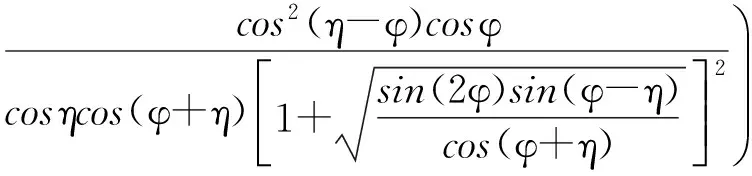
(10)

式(10)可以改为一下这种形式:

(11)

(12)

由Ce表达式可以看出，Ce只和土的内摩擦角φ及地震角η有关,与桥台外形及尺寸无关。因此可根据工程地质手册[15]查得土内摩擦角,或根据当地的现场实验测得；并且与地震角有关的水平地震加速度系数和竖向地震加速度系数也可根据建筑抗震设计规范[16]查得,设计人员可提前根据本地的实际情况确定Ce的取值,在实际设计过程中只需要根据桥台的形式,就可计算出所需土压力值,极大简化了计算过程。

2计算与讨论

笔者设计了5种地震模式,将本文计算方法与Coulomb理论和M-O方法以及林宇亮方法进行对比，如表1所示。具体计算值如表2所示。

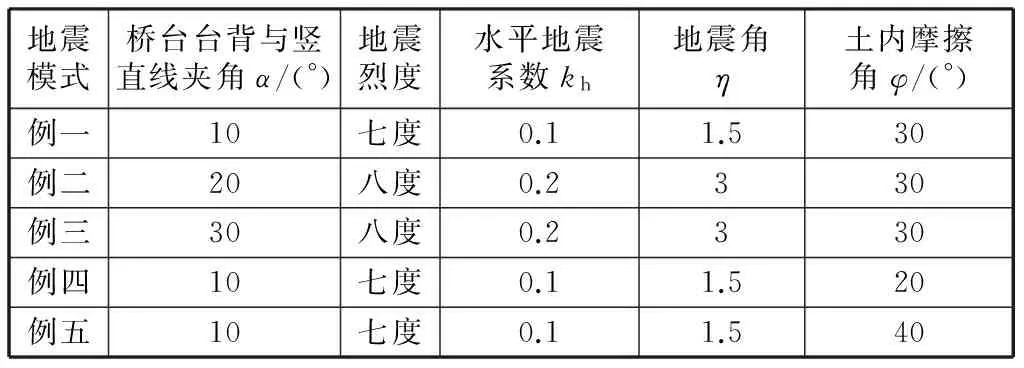
表1　实例参数

分析表2中计算结果可得:本文计算方法得到的结果普遍要比林宇亮方法计算的值大10%以上最大可达40%;本文方法与林宇亮方法得到的结果均比库伦理论得到的值大10%到50%;墙土之间的摩擦角越大,差值越大。主要原因是库伦理论为静力计算理论,并不考虑地震荷载作用。由于地震角偏小,地震荷载对土楔形体受力的影响较小,林宇亮方法和M-O方法计算的结果与库伦理论得到的值相差较小;在不考虑土粘聚力情况下,林宇亮方法与M-O方法计算得到的主动土压力系数基本一致;本文方法在计算过程中考虑了桥台的具体情况,所以得到的结果比其他3种方法方法偏大一些,相对来说也更为安全。

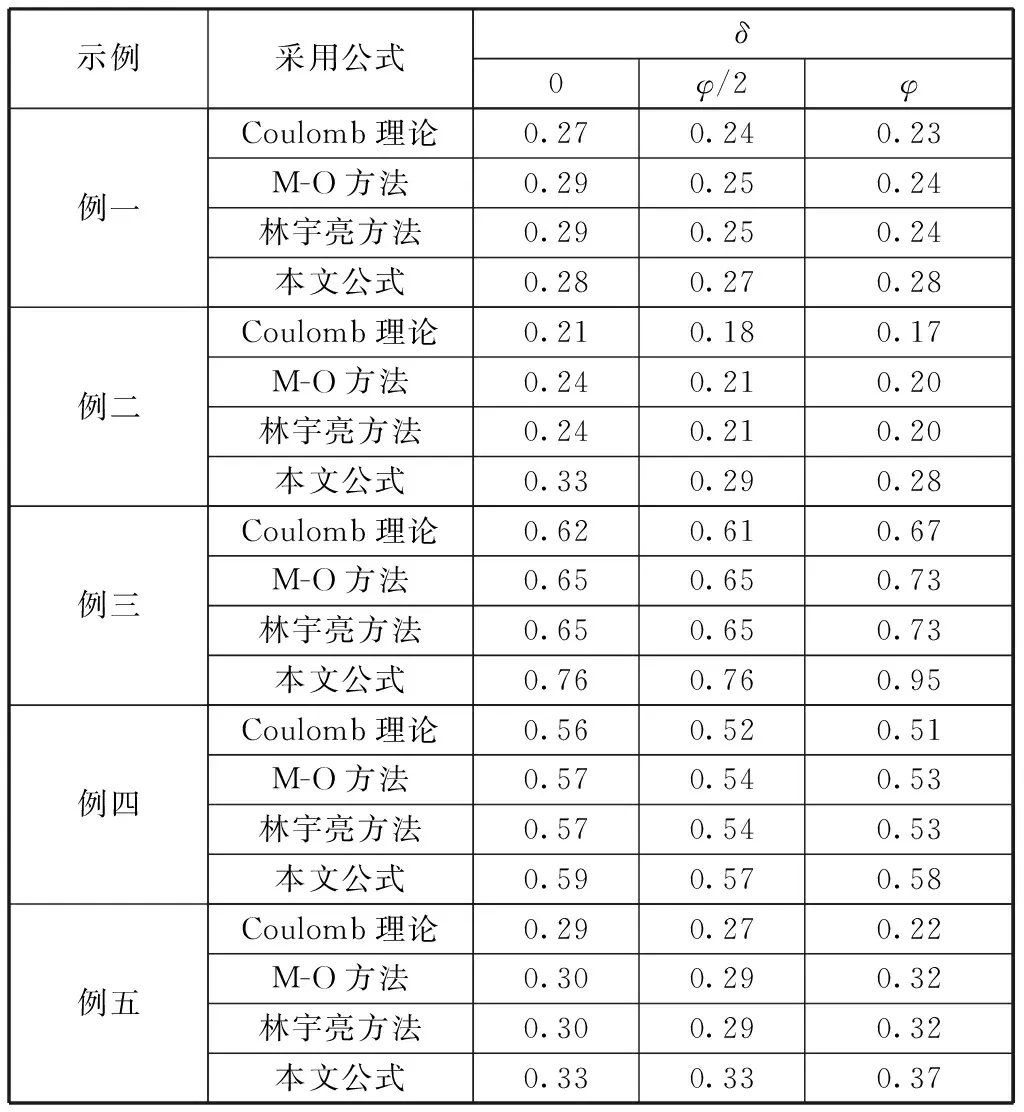
表2　不同公式计算的Kae值

值得一提的是,本文的论述并没有涉及上部结构对桥台土压力的影响,上部结构对于桥台地震响应的影响主要在于:约束增大桥台的惯性,以及约束桥台顶部的水平位移。而在传统的土压力分析理论中,对于挡土墙、桥台的具体位移并不加以分析考虑,计算的思想方法是挡土墙或桥台发生主动或被动位移(包括平移和转动)到极限位置,使得土楔形体达到极限平衡状态,所谓的极限位置为何值,并不考虑。对于桥台来说,由于上部结构的影响,不能像上部自由端一样随意发生位移,要想确定桥台在地震作用时的土压力实际值,必须分析地震时桥台的具体运动形式,采用非极限平衡状态下的土压力计算方法,这一点将是笔者以后的主要研究方向。另外,对于桥台地震土压力的具体分布形式,笔者将在接下来的研究中进行具体的分析与论述,并将采用有限元计算软件进行模拟分析,进一步验证本文公式的准确性与可靠性。

笔者分析了不同内摩擦角条件下,本文方法、Coulomb理论以及M-O方法变化情况,如图5所示。从图中可以看出,随着内摩擦角的增大,主动土压力计算系数不断减小。三种方法随内摩擦角的增大变化趋势相同,进一步验证了本文方法的可靠性,M-O法与库伦土压力理论差值较小,并随内摩擦角的增大逐渐趋于一致。本文方法计算值平均比库伦土压力理论大0.1～0.2,有效地提高了地震条件下主动土压力计算系数,增大了主动土压力计算值,增加了桥台的安全系数。

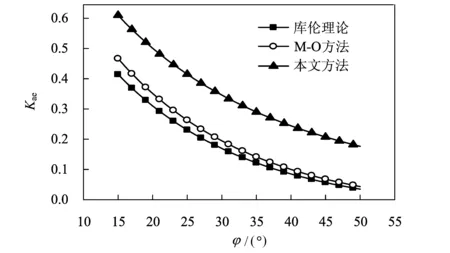
图5　三种计算方法对比Fig.5　Comparison between the methods

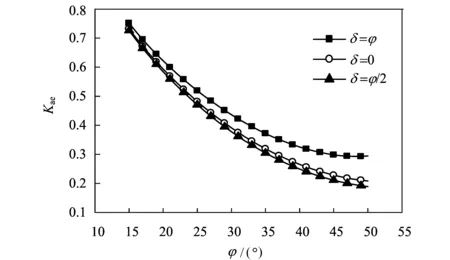
图6　外摩擦角对主动土压力计算系数的影响Fig.6　Effect of external friction angle on the active earth pressure coefficient

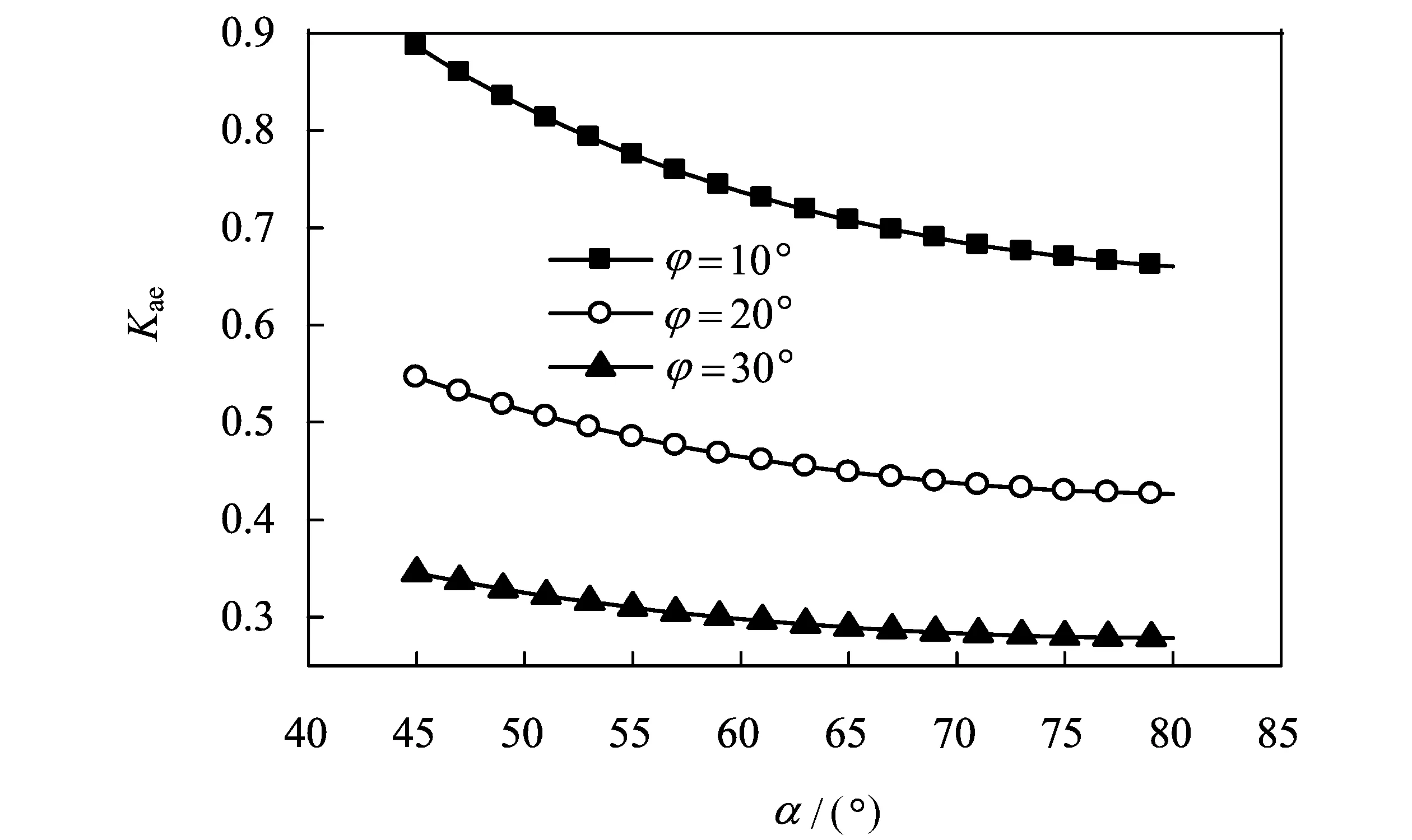
图7　台背倾角对主动土压力系数的影响Fig.7　Effect of abutment angle on the active earth pressure coefficient

图8　不同水平地震加速度系数下内摩擦角对主动土压力系数的影响Fig.8　Effect of external friction angle on the active earthpressure coefficient under different horizontal seismic acceleration coefficient

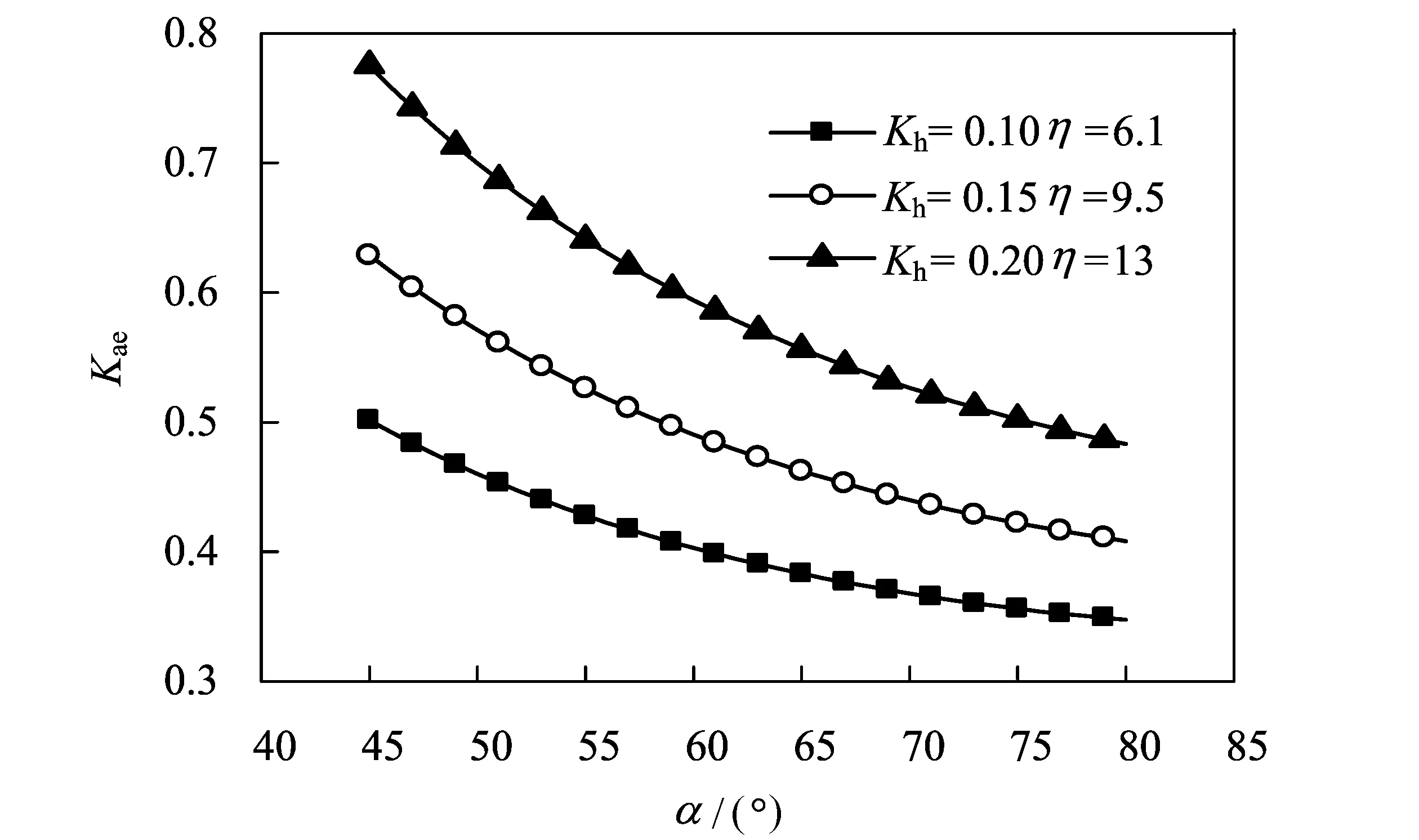
图9　不同水平地震加速度系数下台背倾角对主动土压力计算系数的影响Fig.9　Effect of abutment angle on the active earth pressure coefficient under different horizontal seismic acceleration coefficient

进而,笔者分析了外摩擦角、台背倾角、水平地震加速度系数对于本文公式的影响,如图6至图9所示。从图中可以看出,随着内摩擦角的增大,外摩擦角越大,主动土压力计算系数也越来越大,并且趋势越来越明显；δ在0～φ/2这种趋势并不明显,在φ/2～φ这种变化趋势较为显著。随着内摩擦的增加,主动土压力系数逐渐减小,下降幅度较大,其原因是随着内摩擦角增大,桥台发生位移时,划裂破坏面的角度越大,产生的土楔形体越小,进而其重力和

惯性力均减小,产生的土压力也逐渐降低。另外,随着台背倾角的增大,土压力系数也在减小,其原因为随着台背倾角的增大,台背越来越陡,越来越接近垂直面。从计算过程中,我们可以看出,桥台下侧的土体体积不断减小,产生的惯性力也在减小,进而影响了桥台受到的土压力。水平地震加速度系数越大,主动土压力计算系数越大。

3结论

本文以Coulomb土压力理论为基础,针对桥台的实际特点求得桥台在地震作用下的土压力计算公式,采用图解法得到极限破裂面倾角的解答,并进一步对公式进行简化。结论如下:

1) 简化计算公式随台背倾角、填土内摩擦角变化与库伦土压力理论及M-O方法保持一致,并在台背竖直时,三种计算方法极值相同,验证了简化计算方法的有效性。

2) 通过简化公式计算的结果比传统的M-O方法以及近期林宇亮方法得到的结果大10%到40%,增大桥台设计中土压力值,保证了桥台结构的安全性可靠性。

3) 随着填土的内摩擦角和台背倾角的变化,土压力也发生变化。其规律为:填土的内摩擦角越大,桥台受到的土压力越小;填土的内摩擦角越小,桥台受到的土压力越大;随着台背倾角的增大,台背越接近垂直状态,桥台受到的土压力越小。相比之下,填土内摩擦角的影响更为明显。

4) 水平地震加速度系数越大,地震角越大,桥台主动土压力计算系数也越大。但是,如果填土内摩擦角相差较大的情况下,水平地震加速度系数小的桥台主动土压力计算系数也可能大于水平地震加速度系数大的桥台。

参考文献：

[1]林鹏,黄凯珠,李子昌,等.汶川地震对桥梁结构破坏的影响与启示[M]∥宋胜武.汶川大地震工程震害调查分析与研究.北京：科学出版社，2009:8.

[2]杨剑.地震条件下倾斜挡土墙主动土压力研究[J].岩土工程学报,2009,31(9):1391-1397.

[3]王立强.挡土墙地震土压力大小及其分布[J].中国港湾建设,2007(5):1-5.

[4]STEEDMAN RS,ZENG X.The influence of phase on the calculation of pseudo-static earth pressure on a retaining wall[J].Geotechnique,1990,40(1):103-112.

[5]MYLONAKIS G,KLOUKINAS P,PAPNTONAPOULOS C.An alternative to the Mononobe-Okabe equations for seismic earth pressures[J].Soil Dynamics and Earthquake Engineering,2007,27(10):957-969.

[6]张克恭,刘松玉.土力学[M].北京:中国建筑工业出版社,2010:222-235.

[7]林宇亮,杨果林,赵炼恒,等.地震动土压力水平层分析法[J].岩石力学与工程学报,2010,29(12):2581-2591.

[8]李涛.地震主动土压力简化计算公式[J].铁道工程学报,1996(1):103-105.

[9]梁波.地震条件下桥台台背主动土压力简化计算方法[J].铁道工程学报,1999(2):36-38.

[10]李丹丹,李文华.整体式桥梁台后土压力的试验研究[J].铁道建筑,2014(11):33-36.

[11]李永刚,李俊伟.挡土墙主动土压力非线性分布[J].太原理工大学学报,2004,35(3):196-198.

[12]邓宗伟,冷伍明,聂如松,等.高速铁路桥台台背土压力试验与空间土压力计算分析[J].中国铁道科学,2006,27(6):37-41.

[13]郦能惠,武清玺,陆军,等.挡墙土压力及其分布影响因素的研究[J].岩土工程学报,2013,35(8):1381-1386.

[14]文畅平,杨果林.地震作用下挡土墙位移模式的振动台实验研究[J].岩石力学与工程学报,2011,30(7):1502-1512.

[15]常士骠,张苏民.工程地质手册[M].北京:中国建筑工业出版社,2007.

[16]中华人民共和国建设部.建筑抗震设计规范：GB50011-2010[S].北京:中国建筑工业出版社,2010.

(编辑：贾丽红)

Simplified Approach for Rational Determination of Seismic Induced Earth Pressure on Abutments

LIU Kun1,CHEN Y.Frank1,2,ZHANG Min1

(1.DepartmentofArchitectureandCivilEngineering,TaiyuanUniversityofTechnology,Taiyuan030024，China;2.DepartmentofCivilEngineering,ThePennsylvaniaStateUniversity,MiddletownPA17057,USA)

Abstract:Based on the Coulomb earth pressure theory, this study aims to propose an improved method for calculating seismic-induced earth pressures on abutments with the consideration of actual abutment shapes.The study investigatesd how each system parameter influences the abutment earth pressure and made a comparative analysis between the proposed method and the available methods, including the Coulomb theory, Mononobe-Okabe method, and Lin’s method. The results indicate that:(1)The traditional earth pressure theory tends to give lower or unconservative pressure values by 10%～40%;(2)The larger the backfill friction angle and the abutment back angle are,the smaller the abutment earth pressureis；(3)The degree of the influence of each system parameter on the abutment earth pressure is approximately the same as that predicted by traditional earth pressure theory.

Key words:earthquake;abutment;earth pressure;wedge theory;critical angle.

文章编号:1007-9432(2016)02-0249-05

*收稿日期：2015-07-04

基金项目：国家自然科学基金资助项目：地震波作用下非饱和中PHC管桩水平振动机理研究(51408393)

作者简介：刘坤(1990-)，男，河南濮阳人，硕士生，主要从事桥梁工程方面的研究，(E-mail)874455184@qq.com通讯作者：陈幼佳，教授，博士生导师，主要从事桥梁、结构工程方面研究，(E-mail)yxc2@psu.edu

中图分类号:P315.9

文献标识码:A

DOI：10.16355/j.cnki.issn1007-9432tyut.2016.02.024