自适应小波阈值融合去噪法对采煤机振动信号的处理

张天赐,庞新宇,杨兆建

(太原理工大学 机械工程学院,煤矿综采装备山西省重点实验室,太原 030024)



自适应小波阈值融合去噪法对采煤机振动信号的处理

张天赐,庞新宇,杨兆建

(太原理工大学 机械工程学院,煤矿综采装备山西省重点实验室,太原 030024)

摘要:提出一种自适应小波阈值去噪方法,该方法综合软、硬阈值函数的优点,构建了改进的阈值函数,赋予融合系数μ非定值表达式,使其具有较好的适应性。针对采煤机振动信号采集过程中的背景噪声较大的问题,采取分段阈值的方式,阈值根据信号分解层数的不同来确定。Matlab仿真实验表明,与软、硬阈值去噪法相比,改进的阈值去噪法去噪能力更强,而且能更好地保留原始信号的特征,对原始信号的重构更为准确。运用该方法对采煤机摇臂所采集的振动信号进行去噪处理,有效地去除了高频噪声信号,保留了齿轮啮合频率所在的低频频段,提高了信号的信噪比。

关键词:改进阈值函数;小波变换;信噪比;采煤机振动信号

machine

在实际应用中,传感器拾取的信号不可避免地夹杂了大量噪声,给提取有用信号带来了不便,尤其在强噪声背景下,有用信号的提取更是难上加难。因此如何在强噪声背景下提取微弱的有用信号,对于大型机械设备的故障诊断具有重要意义。

小波分析是近30年来从工程、物理及数学领域发展起来的一门新兴学科,它是继傅里叶分析之后的又一个重大突破,在信号分析和处理领域取得了里程碑式的进展。1994年,斯坦福大学的DONOHO和JOHN-STONE在小波变换的基础上提出了小波阈值去噪的概念[1]。小波阈值去噪由于其多分辨性、选基灵活性、实现简单、计算量小等优点[2],获得了广泛的应用。但由于软、硬阈值函数自身的缺陷,如硬阈值函数存在间断点,软阈值函数存在恒定误差等,这些都引导着国内外学者提出一些改进方法。西安电子科技大学的崔华[3]、东北大学的金晶晶[4]、西北工业大学的赵瑞珍等[5]，都提出了带参数的改进阈值函数,但最佳参数的确定尚无定论。南京航空航天大学的戴维[6]、清华大学的谢杰成[7]提出不同的阈值选取方法,取得了较好的效果,具有一定的借鉴性。笔者从阈值函数与阈值选取的角度出发,提出一种新的改进方法,将已有的硬、软阈值函数进行融合重组,并给予融合系数μ非定值表达式；同时,阈值根据分解层数的不同来确定。通过Matlab仿真，并与已有的方法进行对比,验证了本方法的有效性。运用改进阈值去噪法对采煤机摇臂振动信号进行去噪处理,取得了较好的效果。

1小波阈值去噪原理

在实际应用中,采集到的信号f(t)中夹杂着大量噪声,因此可将f(t)表示成式(1)的形式。

(1)

式中:f(t)为采集到的含噪信号;x(t)为有用信号;n(t)为噪声。

小波阈值去噪的目的就是尽可能地将有用信号x(t)和噪声n(t)分离,保留有用信号x(t),去除噪声n(t)。其主要理论依据是经过正交小波分解后,有用信号的小波系数幅值要大于噪声的系数幅值[8]。具体处理过程为:将含噪信号在各尺度上进行分解,保留低分辨率下的全部分解值；对于高分辨率下的分解值设定一个阈值,幅值低于该阈值的小波系数置为零,高于该阈值的小波系数完整保留或者收缩；最后将处理后获得的小波系数利用逆小波变换进行重构,恢复出有用信号。图1是其流程图。

图1　小波阈值去噪法流程图Fig.1　The flow chat of a adaptive wavelet threshold denoising method

小波阈值去噪法一般分为以下3步:

1) 将含噪信号f(t)作小波变换,得到一组小波系数wj,k;

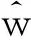
3) 利用新的小波系数进行小波重构,得到新的信号即为去噪后的信号。

小波系数wj,k表示第j层小波分解分量的第k个系数。根据不同的小波系数估计方法,对应不同的小波阈值估计函数,通用的有硬阈值函数和软阈值函数[9]。

(2)

1.2硬阈值函数

(3)

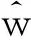
2改进的阈值去噪方法

2.1改进阈值函数

由于单一的使用软、硬阈值函数去噪效果并不理想,因此笔者将两种方法进行融合重组,得出新的阈值函数式:

(4)式中,0≤μ≤1。当μ=0时，相当于软阈值函数；当μ=1时,相当于硬阈值函数。这种方法关键点在于融合系数μ的取值问题；但无论μ取任何值,都仅仅是将软阈值函数或者硬阈值函数的误差进行一定程度的减少,并且需要大量的实验来获取μ的最佳取值[11],造成了很大的不便。因此,基于以上问题,笔者采取μ为非定值的方法。令：

当|wj,k|较大时,说明噪声信号中突变较多,此时μ增加,折衷函数偏向于硬阈值函数,有很好的去噪能力;当wj,k较小时,说明噪声信号较为平滑稳定,此时μ减小,折衷函数偏向软阈值函数,有很好的光滑性。因此,本方法中的μ具有一定的自适应性,去噪效果更好。

2.2阈值的选取

3仿真实验及采煤机振动信号处理

3.1仿真实验

本文使用Matlab2012a平台进行仿真实验,采用仿真机械振动信号。该信号由调幅频率20Hz,基频10Hz,调频频率40Hz的调幅调频信号和频率为130Hz的正弦信号叠加,表达式为:

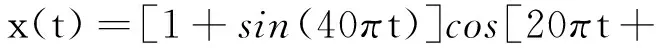
(5)

图2　仿真振动信号时域波形Fig.2　Time domain waveform of the simulation of vibration signal

对该信号添加高斯随机噪声,采用dB8小波进行4层分解,使用软、硬阈值去噪和改进的去噪方法分别进行去噪仿真；并对去噪信号进行频谱分析,使用信噪比(RSN)跟均方误差(EMS)为指标对比实验效果。仿真振动信号时域波形如图2所示；频谱分析如图3所示；硬阈值去噪、软阈值去噪及改进阈值去噪后振动信号的频谱分析如图4-图6所示。

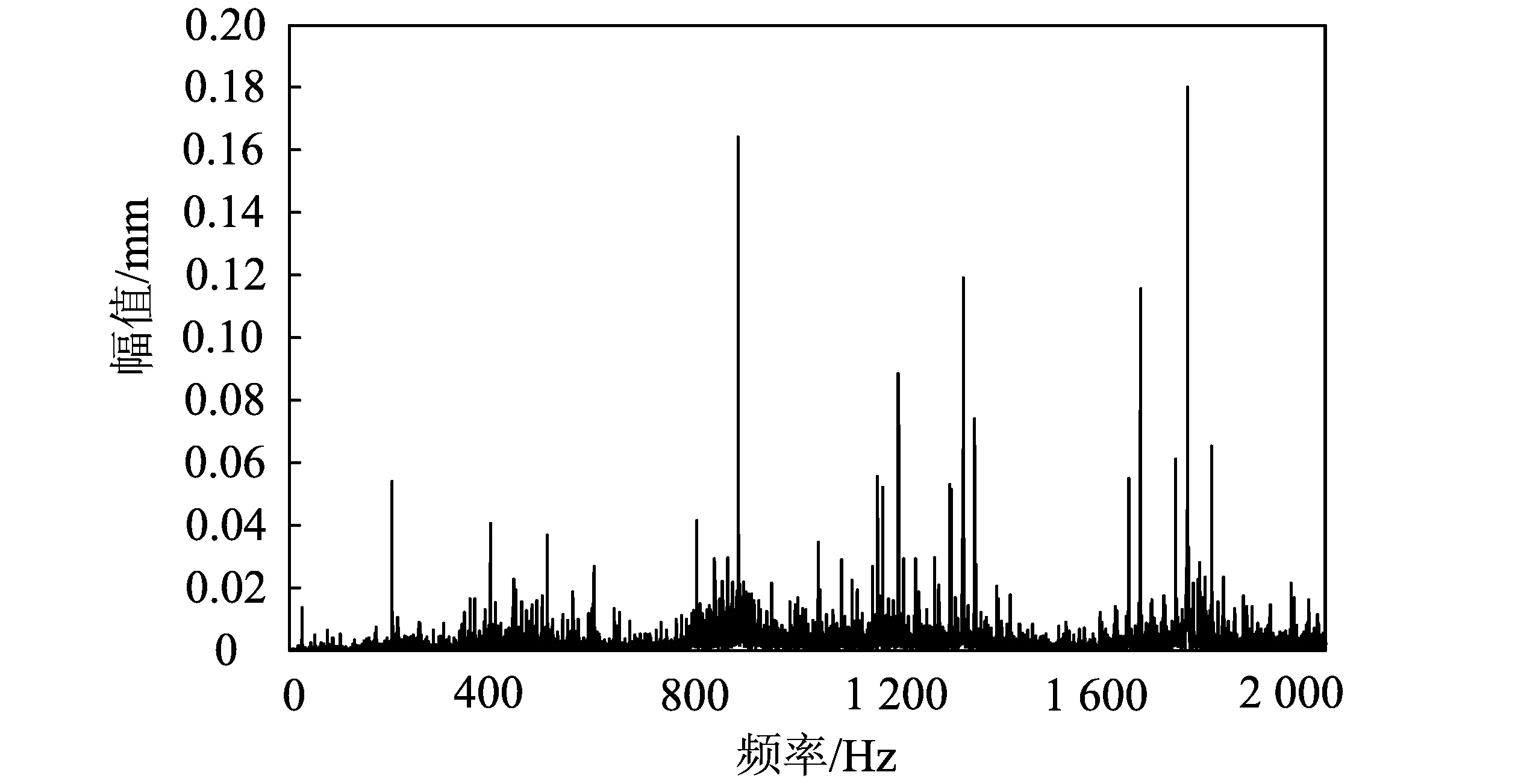
图3　仿真振动信号频谱图Fig.3　Frequency spectrogram of the simulation of vibration signal

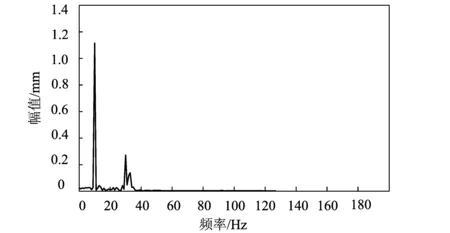
图4　硬阈值去噪频谱图Fig.4　Frequency spectrogram of hard threshold denoising method

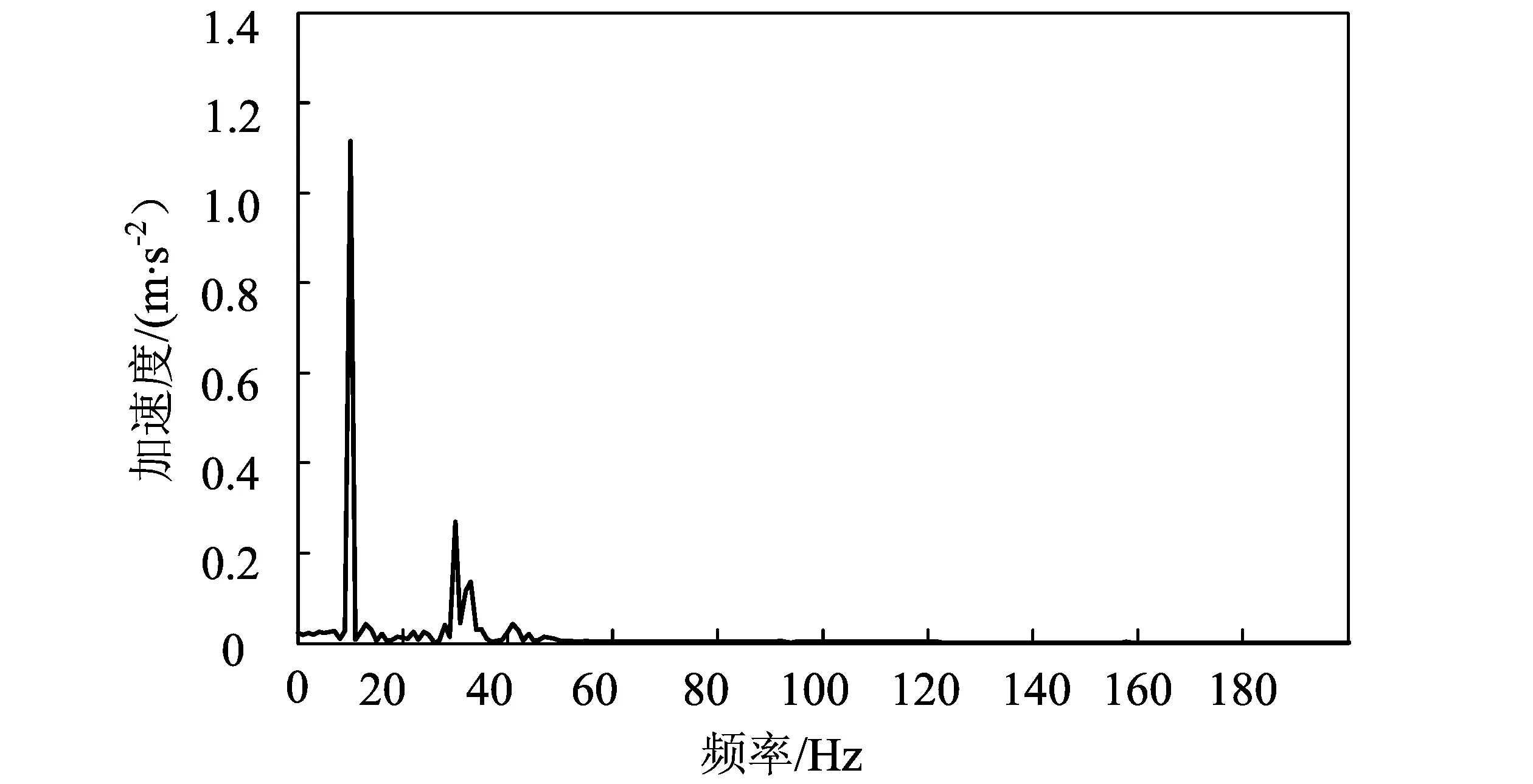
图5　软阈值去噪频谱图Fig.5　Frequency spectrogram of soft threshold denoising method

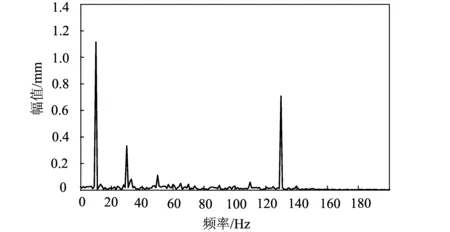
图6　改进阈值去噪频谱图Fig.6　Frequency spectrogram of improved threshold denoising method

该仿真信号的有用信号集中在10,30,50,130 Hz处,其余为添加的高斯白噪声。从图3-图5综合来看,软、硬阈值法由于阈值选取过大将60 Hz之后的信号全部消除,同时50,130 Hz的有用信号被消除。改进阈值去噪方法不仅将信噪比提高到了4.314 7 dB,均方误差减小到了0.486 7；而且从图6可以看出,改进阈值去噪法对信号的还原较为完整,消除了大部分低幅值噪声,极大地提高了去噪后的信号质量。试验表明，改进阈值去噪后的信号提高了信噪比,减小了均方误差,更好地保留了有用信号,具有良好的效果。不同方法去噪效果如表1所示。

表1　不同方法去噪效果对比

3.2采煤机振动信号处理

试验在采煤机摇臂加载试验台上进行,分别在低速端和高速端壳体外部安装了两个振动加速度传感器,用于采集摇臂壳体振动信号。采煤机摇臂负载转矩为370 N·m,输入转速为1 500 r/min。经计算,采煤机摇臂传动部分各齿轮的旋转频率在2.24～25 Hz之间,各齿轮啮合频率分布在46.24～870 Hz之间。分析以高速端振动信号为例。

图7为试验采集的部分振动信号的时域波形,从时域波形得不到相关的特征频率信息,因此对其进行频谱分析,如图8所示。采用传统的硬、软阈值去噪法对振动信号进行去噪,去噪后的振动信号频谱图如图9所示,两种方法得到的频谱图完全相同。这是由于实际采集过程中,背景噪声较大,造成噪声方差σ较大,从而阈值变大,这样就造成小波分解中高频系数经阈值处理后全部变为0,信号重构过程以未经处理的低频系数进行重构,使得硬、软阈值去噪法得到了相同的结果；同时由于阈值过大,将400 Hz之后的部分齿轮啮合频率去除,造成了过度去噪现象。

采用改进的阈值去噪法对振动信号进行处理,其频谱图如图10所示。从图中可以看出,重构信号完整地保留了0～870 Hz的有用信号,去除了1 000 Hz之后的大部分高频噪声；同时重构信号突出了齿轮啮合频率所在的低频频段,为下一步的信号分析提供了方便。具体效果对比如表2所示,改进阈值去噪法在RSN和EMS方面都具有明显的优势。

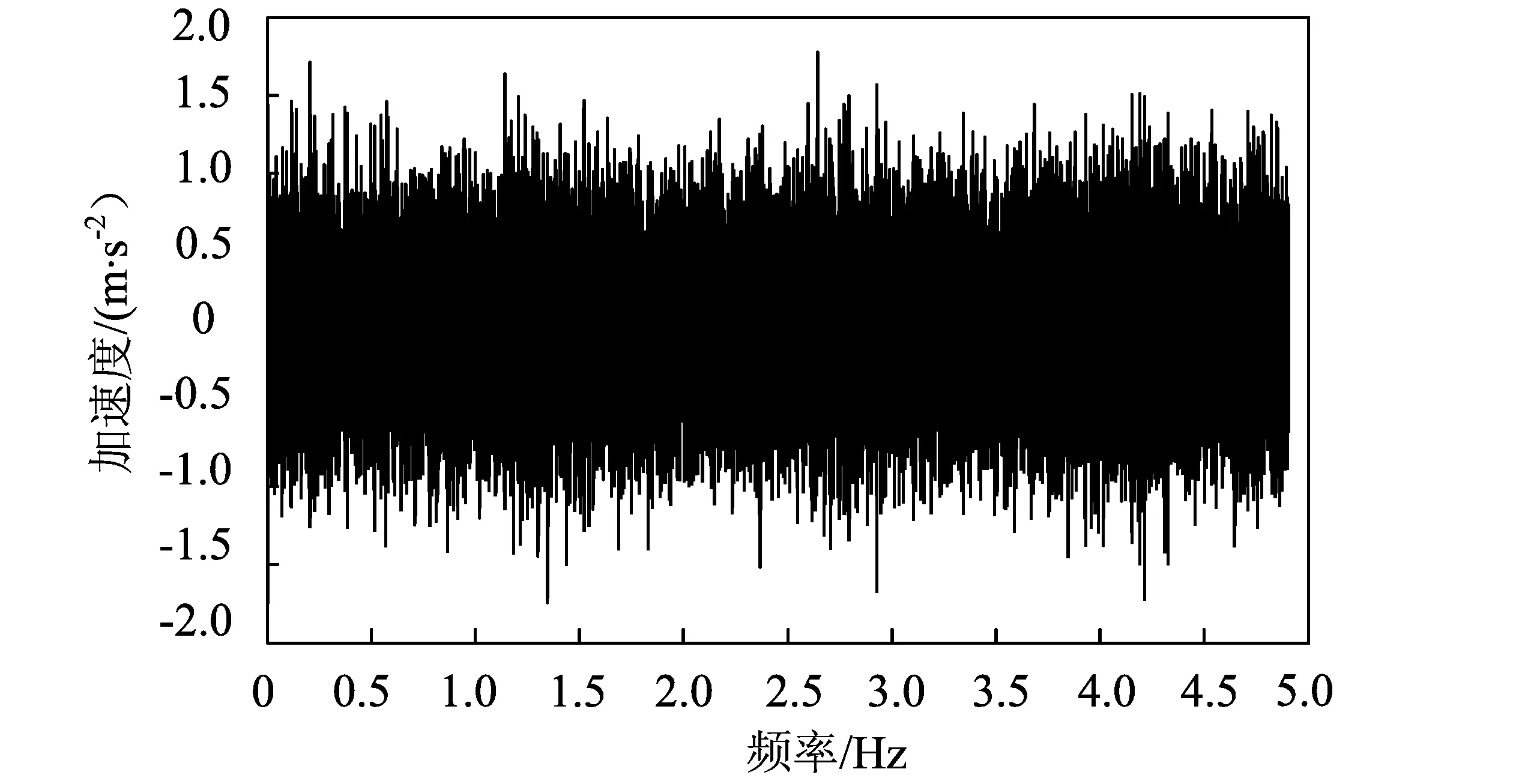
图7　试验采集的部分振动信号Fig.7　Partial vibrational signals acquired through the tests

图8　试验采集的振动信号频谱图Fig.8　Frequency spectrogram of the vibrational signals acquired through the test

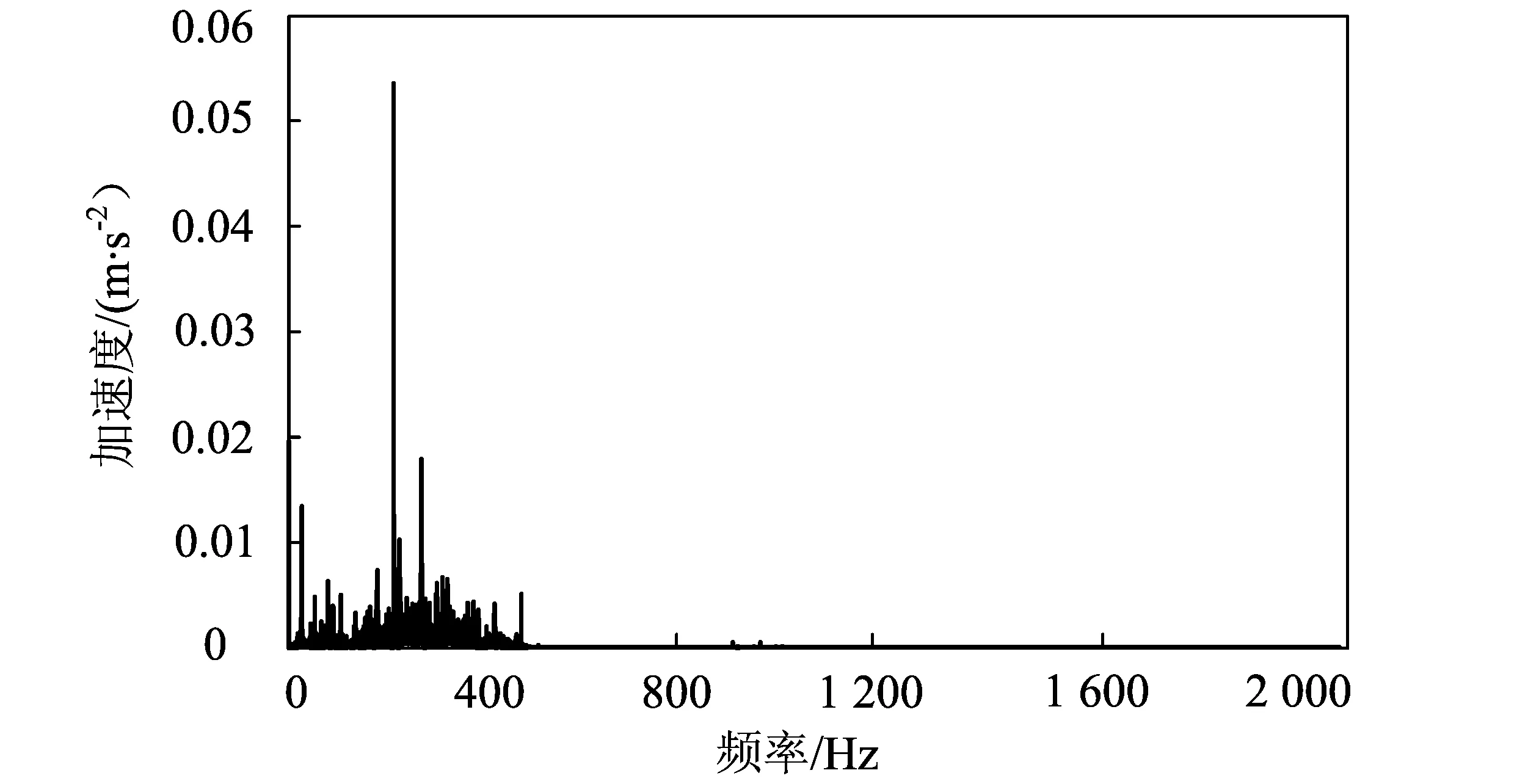
图9　硬阈值、软阈值去噪后得到的相同振动信号频谱图Fig.9　Same vibration signal spectrum of hard threshold and soft threshold denosing

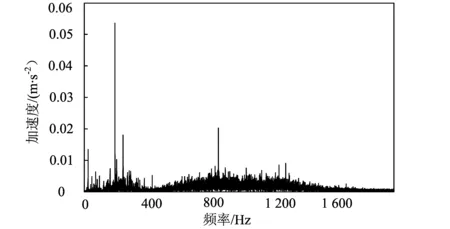
图10　改进阈值去噪后的振动信号频谱图Fig.10　Vibration signal spectrum of improved threshold denosing method

去噪指标硬阈值去噪软阈值去噪改进阈值去噪信噪比RSN0.29290.29290.4117均方误差EMS0.03470.03470.0238

4结束语

小波分析在处理非稳态信号上有其独特的优势,基于小波分析的小波阈值去噪为我们提供了一种新的去噪思路。在针对采煤机摇臂的振动信号去噪中,由于背景噪声较大,传统的硬、软阈值去噪法阈值选取较大,对高频噪声进行了有效的抑制,但却由于阈值过大消除了一定的有用信号。笔者提出的改进阈值去噪法,提出了一个新的自适应阈值函数,能够在处理低频信号中采用偏软

阈值去噪,在处理高频信号采用偏硬阈值去噪；同时针对阈值选取过大的问题,采取分段阈值的方法,对每一段阈值进行了线性的减小。实验表明,在对采煤机摇臂振动信号去噪中,该方法取得了较好的效果。

参考文献：

[1]DONOHO D L,JOHNSTONE J M.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika,1994,81(3):425-455.

[2]王拴中,朱玉田.改进小波阈值去噪法的对比性仿真实验与分析[J].噪声与振动控制,2012,32(1):128-132.

[3]崔华,宋国乡.基于小波阈值去噪方法的一种改进方案[J].天津农学院学报,2005,28(1):8-10.

[4]金晶晶,王旭,吴雪,等.基于改进阈值函数的体震信号平移不变去噪[J].东北大学学报(自然科学版),2009,30(3):333-336.

[5]赵瑞珍,宋国乡,王红.小波系数阈值估计的改进模型[J].西北工业大学学报,2001,19(4):625-628.

[6]戴维,于盛林,孙栓.基于Contourlet变换自适应阈值的图像去噪算法[J].电子学报,2007,35(10):1939-1943.

[7]谢杰成,张大力,徐文立.一种小波去噪方法的几点改进[J].清华大学学报(自然科学版),2002,42(9):1269-1272.

[8]岑翼刚,尉宇,孙德宝.小波阈值神经网络在信号去噪及预测中的应用[J].控制理论与应用,2008,25(3):485-491.

[9]李博,吴伟,周密.基于LabVIEW的小波阈值融合算法去噪分析[J].西安石油大学学报(自然科学版),2010,25(2):76-80.

[10]苑津莎,张冬雪,李中.基于改进阈值法的小波去噪算法研究[J].华北电力大学学报(自然科学版),2010,37(5):92-97.

[11]李祥兵,肖合林.基于Matlab的小波阈值折衷去噪算法研究[J].电脑开发与应用,2009,22(6):4-6.

[12]DAUBECHIES I,HEIL C.Ten lectures on wavelets[J].Computers in Physics,1992,6(3):1671.

(编辑：庞富祥)

Adaptive Wavelet Threshold Confluent Denoising Method for Coal Minning Machine Vibration Signal Processing

ZHANG Tianci,PANG Xinyu,YANG Zhaojian

(CollegeofMechanicalEngineering,ShanxiKeyLaboratoryofFullyMechanizedCoalMiningEquipment,TaiyuanUniversityofTechnology,Taiyuan030024,China)

Abstract:This paper presents a kind of adaptive wavelet threshold denoising method. A new threshod function is built by combining the advantages of soft and hard threshold functions in the method，which gives confluent quotiety a non-constant expression, and has better adaptability.Besides,aiming at the big background noise in the process of coal mining machine vibration signal acquisition,the authors take the form of segmental threshold,which can be determinded according to the different number of signal decomposition layers. The results of the Matlab simulation show that the denoising method has stronger denoising ability.Compared with the soft and hard threshold denoising method, the new method has better ability to remain the characterisitics of original signal,and is more accurate in original signal refactoring.By denoising the vibration signal collected from the coal mining machine with this method, high frequency noise signal is eliminated and low frequency band is remained where meshing frequency of gear is located,then higher SNR is obtained.

Key words:improved threshold function;wavelet transform;SNR;vibration signal of coal mining

文章编号:1007-9432(2016)02-0170-04

*收稿日期：2015-10-26

基金项目：国家自然科学基金资助项目：基于振动与电机电流信息融合的转子系统载荷识别及故障诊断方法(51475318);山西省青年科技研究基金资助项目：扭矩激励下转子系统磨损机理与试验研究(2014021024-2 )；太原理工大学校青年团队项目(2013T035)

作者简介：张天赐(1993-)，男，山西临汾人，硕士生，主要从事煤矿机械故障诊断的研究，(E-mail)ztc1213@foxmail.com通讯作者：庞新宇，副教授，主要从事机械故障诊断方面的研究工作，(E-mail)typangxy@163.com；杨兆建，教授，主要从事机械设计及理论研究，(E-mail)yangzhaojian@tyut.edu.cn

中图分类号:TP206.3

文献标识码:A

DOI：10.16355/j.cnki.issn1007-9432tyut.2016.02.009