基于多目标优化的数控实时任务参数选择方法*

翟振坤　李迪

(华南理工大学 机械与汽车工程学院， 广东 广州 510640)

基于多目标优化的数控实时任务参数选择方法*

翟振坤李迪

(华南理工大学 机械与汽车工程学院， 广东 广州 510640)

摘要：针对协同设计模式下数控实时任务参数的选择问题,提出一种基于多目标优化的任务参数选择方法.该方法依据实时任务模型、性能目标以及系统约束建立数控任务参数选择问题的多目标优化模型.对于优化模型的求解,提出一种具备协同进化算子与精英团队保留机制的扩展型非支配排序遗传算法,以实现在大规模决策空间下的快速搜索，使得数控系统整体性能目标最优.最后,基于仿真实验分析总结了数控实时任务参数选择策略,通过对比传统任务参数选择方法证明了所提方法在实际应用中的优越性.�

关键词：数控系统；多目标优化；实时控制；进化计算

嵌入式数控系统设计中,插补与位控等数控功能可由一组实时任务来实现.特定调度策略下,执行周期、截止期限、优先级等实时任务参数的选择,不仅决定了任务集的可调度性,而且不良的参数设置会引起任务的抖动与延迟进而影响数控系统的整体性能[1].因此,如何正确地选择实时任务参数是嵌入式数控系统设计过程中需要解决的关键问题.

控制与实时调度间的分离式、协同式设计是两类常用的嵌入式控制系统设计模式[2-3].分离设计模式下,实时任务参数的选择由控制性能需求决定.由于没有兼顾可调度性需求,实时调度中可能引起任务的不可调度,进而影响实现阶段的系统性能.针对此类问题,文献[4]基于弹性周期模型,提出一种可获得最小超周期的任务周期选择算法,在满足可调度性需求的同时,将对任务周期的假设扩大到特定区间,增加了控制设计的灵活性,利于保障系统性能.文献[5]在控制设计中利用形式化方法验证数控任务间逻辑执行顺序的正确性,并针对可调度性需求推导了各任务所需执行时间分配的相对值.由于分离式设计不总以最优方式利用可用资源,在资源有限的情况下,不利于获得最佳的系统性能[6].

协同设计模式下,实时任务参数、资源约束、系统性能等因素间的耦合关系被描述为最优化问题[7-8],实时任务参数的选择等价于对优化问题的求解.文献[9]通过推导任务周期、相对截止期限与系统性能损耗间的量化模型,利用最早截止时间优先算法(EDF)可调度性约束求取使得性能损耗最小的最优任务参数.文献[10]将任务周期的选择描述为二次规划问题,利用梯度下降法求解满足稳定性与可调度性约束的最优任务周期.文献[11]研究了任务的延迟、抖动和周期、优先级分配间的相关性,并以稳定性为目标,提出一种任务优先级分配算法.需要指出的是，上述研究中均假设任务运行期间相互独立，无执行次序约束,但数控系统中插补、位控等实时任务在运行过程中互不独立并且相互间存在时序约束,因此已有方法并不适用于数控实时任务参数选择.此外,工程应用中除稳定性外,数控系统还需满足精度、速度和能耗等多类相互共存与冲突的性能目标,但目前还鲜见基于多目标优化的数控实时任务参数选择方法的研究.

为深入研究协同设计模式下数控实时任务参数的选择问题,文中提出利用基于Pareto最优的多目标优化方法,依据可调度性、稳定性约束,在任务参数可行域内搜索使得精度、速度和能耗等性能目标最优的数控实时任务参数.同时,为提高大规模决策空间下最优任务参数的搜索效率,提出一种具备协同进化算子与精英团队保留机制的扩展型非支配排序遗传算法II(ENSGA-II).最后,以两轴数控系统为例,通过仿真实验对任务参数选择策略等问题进行了分析与验证.

1数控实时任务模型

文中假设采用固定优先级抢占式调度策略,如图1所示,调度过程中ri,k、si,k、fi,k为i在第k次执行中的释放、开始和完成时刻.假定任务在释放时刻对输入进行采样,则响应时间Ri,k=fi,k-ri,k，代表任务的输入输出延迟.受抢占、同步等因素的影响,Ri,k是时变的,为描述其不确定性,如式(1)所示,定义名义延迟Li和最坏响应时间抖动[11]:

(1)

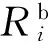
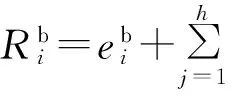
(2)

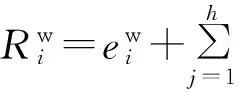
(3)

式中,h表示任务优先级高于i的任务j的个数,取整算子「⎤用于计算调度过程中j的执行次数.公式的求解基于固定点迭代,其初始条件为与.

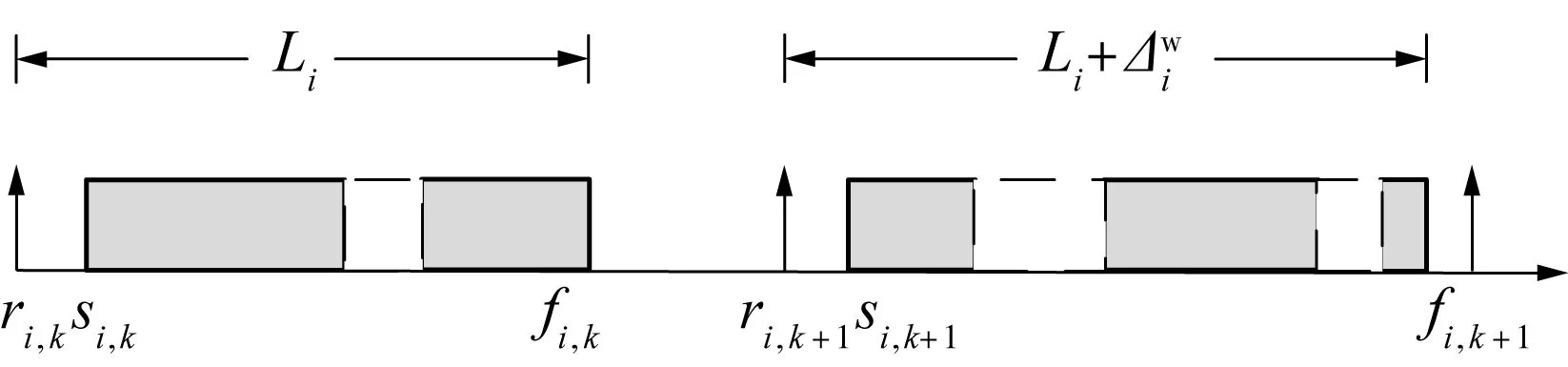
图1 实时任务模型Fig.1 Real-time task model

实时调度过程中,数控任务参数的取值会影响控制系统的整体性能,任务参数的选择过程中需要满足下述系统约束.

(1) 可调度性约束

对于数控实时任务集Γ,当且仅当式(4)成立时,Γ是可调度的.

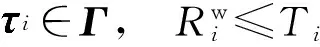
(4)

(2) 稳定性约束

如前所述,数控任务的响应时间存在不确定性,由此产生的延迟与抖动可能造成控制系统的不稳定.依据文献[11],任务i的响应时间与控制系统稳定性间的耦合关系可由线性不等式(5)近似表征.

(5)

其中,αi和βi为已知的线性模型中的系数,结合式(1),稳定性约束可进一步表示为

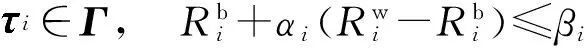
(6)

2基于多目标优化的任务参数选择

2.1多目标优化建模

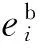
决策空间X中的点代表了不同的任务参数分配方案,依据加工误差、加工时间和CPU使用率等典型的数控系统性能目标,可从精度、速度和能耗等角度衡量各分配方案下数控系统的整体性能.

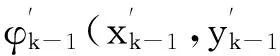
εk≈-εx,ksinθ+εy,kcosθ

(7)

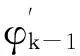
(8)

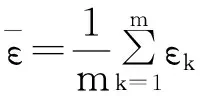
对于加工时间的衡量,工程上可通过模拟执行加工程序来近似估计实际的加工时间.假设在仿真过程中加工程序在时刻ws开始执行,并在时刻we执行结束,则加工时间可表示为

w=we-ws

(9)

嵌入式平台下,系统资源是有限的.文中以CPU使用率为指标来衡量数控系统在执行过程中的性能损耗.对于任务i,调度过程中其总的运行时间为

(10)

其中，ei,g为i在第g次执行中的实际执行时间,表示任务i总的执行次数.

当加工时间为w时,CPU使用率的定义如下:

(11)

综上,基于多目标优化的数控实时任务参数选择问题可表述为:在系统约束条件下,在决策空间中搜索使得各类性能目标同时达到最优的实时任务参数集,此类多目标优化问题的数学模型如下所示:

min y=[ε*(X),w(X),u(X)]T

(12)

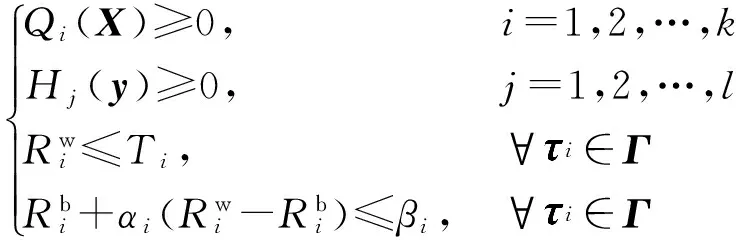
其中，y为性能目标向量,Qi(X)和Hj(y)代表与决策空间和性能目标有关的约束条件.

2.2基于ENSGA-II算法的优化模型求解

2.2.1决策空间复杂度分析

2.2.2ENSGA-II算法

NSGA-II[13]是一类经典的多目标优化问题求解算法,由于本身缺乏种群间的协作进化机制,影响了其在大规模决策空间应用中的收敛速度[14].协同进化通过对待解问题决策空间进行种群划分,强调进化过程中种群间的交互与协调,与传统算法相比具有更好的搜索能力[15].基于协同进化思想,文中提出一种ENSGA-II算法用于搜索最优数控实时任务参数.所提算法通过引入协同进化算子以及精英团队保留机制来提高求解算法的搜索能力和收敛速度.

定义1设ci、cj为子空间Sci、Scj中的进化子种群,种群间相互支配个体数之差Nc定义为

Nc=ci-cj

(13)

当Nc取Z+、0和Z-时,代表ci中支配cj的个体数大于、等于和小于cj中支配ci的个体数.

定义2对于Sci中的进化子种群ci={a1,a2,…,an},设av={Jv1,Jv2,…,Jvm}与aq={Jq1,Jq2,…,Jqm}表示子种群包含的任意两个个体,ci的种群分布ρi由式(14)定义.

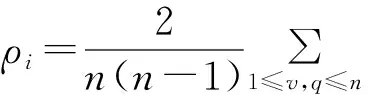
(14)

其中,范数‖‖代表子种群中个体间的距离,文中为欧几里得距离.种群分布描述了种群个体的聚集程度，其取值越大表示种群分布性越好.

定义3假设ci、cj为任意两个进化子种群,当且仅当Nc>0或Nc=0且ρi>ρj成立时,子种群占优算子≻c可定义为偏序关系ci≻ccj.

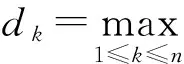
(15)

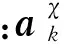
ENSGA-II算法描述如下:

步骤1将决策空间划分为N个子空间,令进化代数te=0,基于NSGA-II产生n维初始精英团队E(te);

步骤2随机选择Np个子空间,令t=0,在每个子空间上产生一个n维初始子种群ci(t),1≤i≤Np;

步骤3在每个子空间上,应用NSGA-II(ci),1≤i≤Np独立进化Nσ代,在≻c偏序关系下,对所有ci(t+Nσ),1≤i≤Np进行排序,从排在前列的子种群中选出n个最优个体,t←t+Nσ;

步骤4将步骤3中选出的n个最优个体逐个与精英团队中的个体进行比较,如果存在支配关系，则替换掉相应的最差精英个体，并更新精英团队E(te),te←te+1;

步骤5从N-Np个子空间中随机选择Nr个新子空间并且每个新子空间上产生一个n维子种群,与步骤3中已排序的ci(t),1≤i≤Np中排在后Nr个的子种群分别利用≻χ进行交叉,并用新种群替代原Nr个子种群;

步骤6判断是否达到算法结束条件,若是则转步骤7,否则转到步骤3;

步骤7输出E(te),算法结束.

3实施方案

一般的多目标优化问题中,性能目标是定义在决策空间上的数值函数.但对数控任务参数选择问题而言,由于决策空间内的任务参数与性能目标间不存在直接的映射关系,无法以数值函数描述二者的关联性,从而限制了ENSGA-II算法的实施.

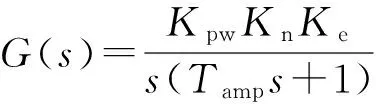
4仿真实验及分析

文中以两轴数控系统中的运动控制单元设计为例,通过仿真实验验证所提方法的有效性.假设协同设计模型中,运动控制单元包含的代码解析、插书补、位控和通信等核心功能被封装为4个优先级互不相同的实时任务1—4,任务参数约束为:对于1,0.3 s≤T1≤0.6 s,递增量为=0.1 s；对于2—4,0.003 s≤T2-T4≤0.007 s,递增量为).受控对象传递函数模型中Kpw=2-15,Kn=5,Ke=32 768,Tamp=0.01.仿真过程中,假设参考轨迹为半径r=5 cm的圆,进给速度为1 mm/s,采用梯形加减速算法并设定初始与结束速度均为0,加速度为0.04mm/s2,减速度为0.03 mm/s2.性能目标的约束条件为:εmax≤2 mm,w≤3 s,u<100 %.

ENSGA-II算法中的参数取值如下:总迭代次数Nite=500,NSGA-II算法中的交叉概率Bc=0.9、变异概率Bm=0.01,子种群交叉概率BNc=1,子空间划分数N=81,初始子种群数目Np=10,精英团队维数n=10,独立进化代数Nσ=20,交叉子种群数目Nr=5,交叉系数ξ=0.7.基于以上参数设置,运行ENSGA-II算法与协同设计模型,经过Nite次迭代后,得到的任务参数Pareto最优解集及其对应的性能目标如表1所示.以第3组参数方案为例,当4个数控任务参数取表中的t1—p4值时,其对应的加工误差为0.091 9mm,加工时间为1.6s,CPU使用率为24.97 %,所得结果均满足性能目标约束.

表1精英团体中的Pareto最优解集

Table 1Pareto optimal solution set in the elite group

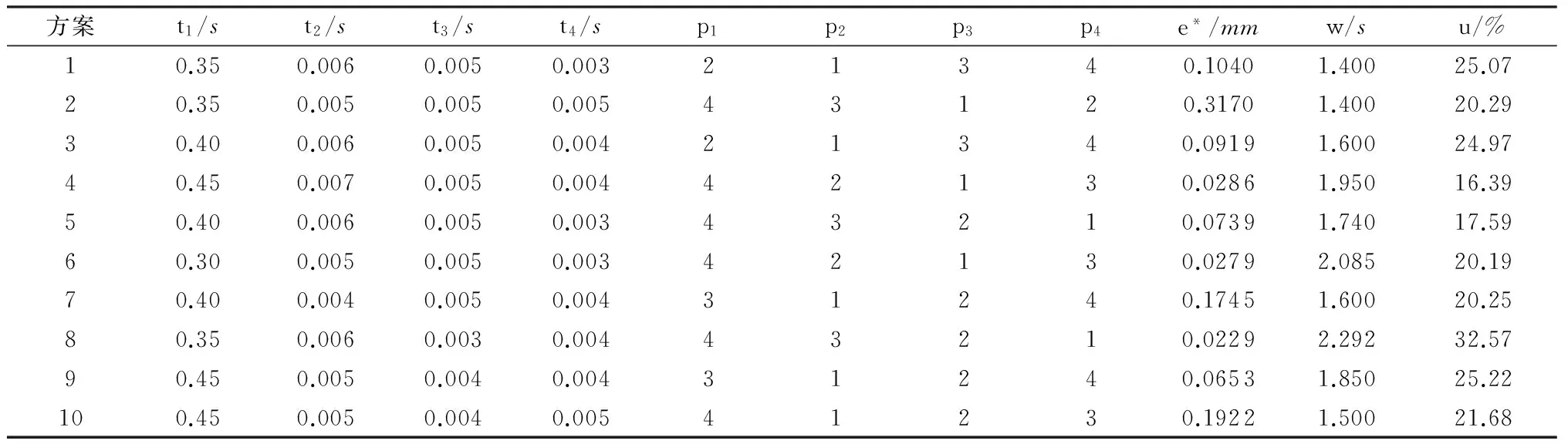
方案t1/st2/st3/st4/sp1p2p3p4e*/mmw/su/%10.350.0060.0050.00321340.10401.40025.0720.350.0050.0050.00543120.31701.40020.2930.400.0060.0050.00421340.09191.60024.9740.450.0070.0050.00442130.02861.95016.3950.400.0060.0050.00343210.07391.74017.5960.300.0050.0050.00342130.02792.08520.1970.400.0040.0050.00431240.17451.60020.2580.350.0060.0030.00443210.02292.29232.5790.450.0050.0040.00431240.06531.85025.22100.450.0050.0040.00541230.19221.50021.68

4.1数控实时任务参数选择策略

多目标优化问题中,性能目标间通常是相互冲突的,为达到整体性能的最优,在最优解的选择过程中需要依据性能需求对各个子目标进行综合考虑.

图2给出了第2、3、6、7组参数选择方案下相应的CPU使用率和加工时间对比,图3(a)-3(d)给出了4组任务参数下的轮廓误差分布对比.由图2可知,第2组任务参数下的加工时间最短(1.400s),CPU使用率低(20.29 %).图3(a)所示较大的轮廓误差峰值(2.349mm)和标准差(0.317mm)表明其加工精度相对较低,因此本组任务参数适用于对效率、能耗要求高,而对精度要求相对较低的应用场合.比较而言,第6组任务参数下,虽然其加工时间较长(2.085s),但CPU使用率较低(20.19 %)，且由图3(c)可知其轮廓误差峰值(0.095mm)与标准差(0.028mm)较小,因此本组任务参数适用于对精度、能耗要求苛刻,对效率要求相对较低的应用场合.

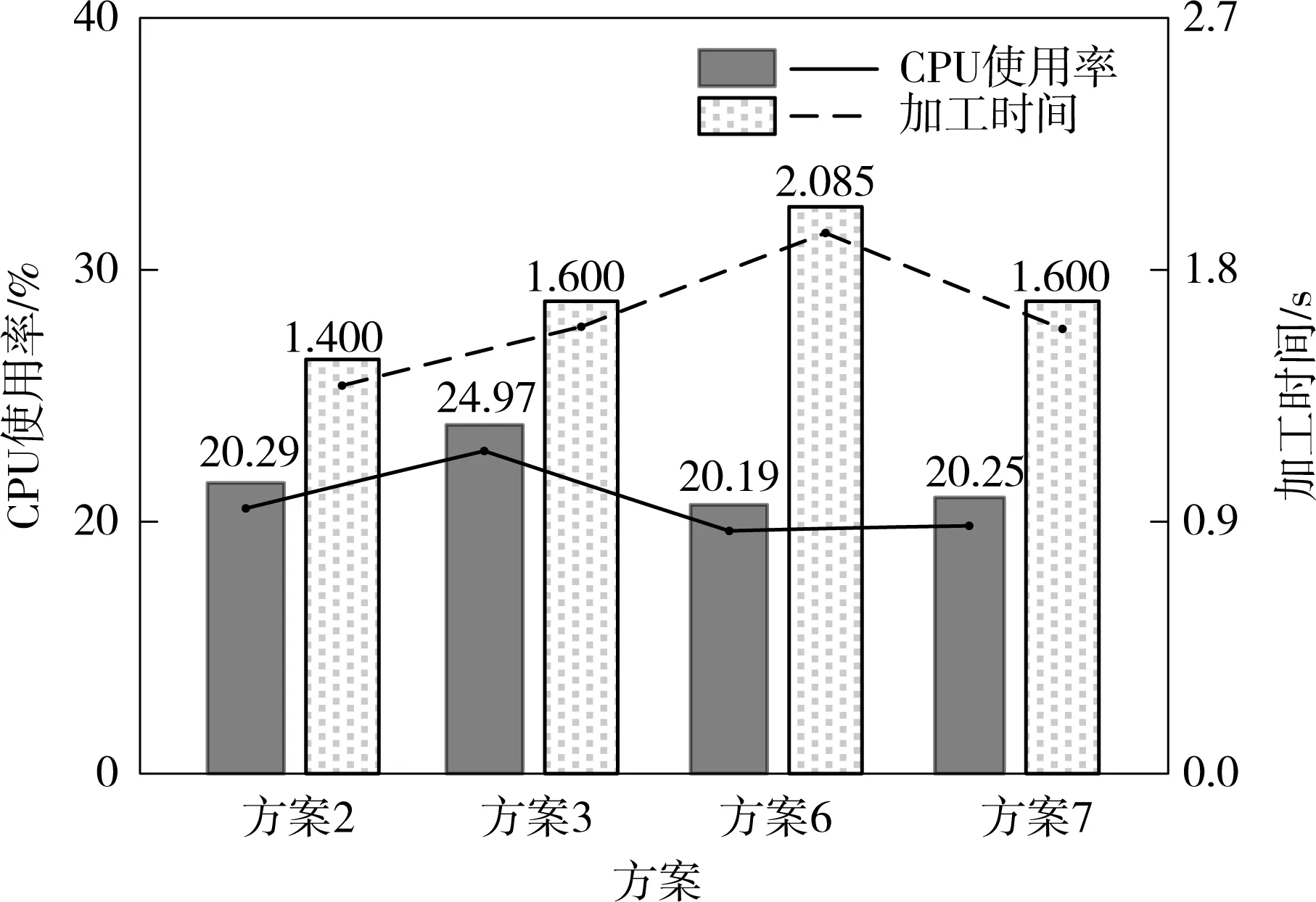
图2　CPU使用率与加工时间对比Fig.2　CPU utilization and machining time

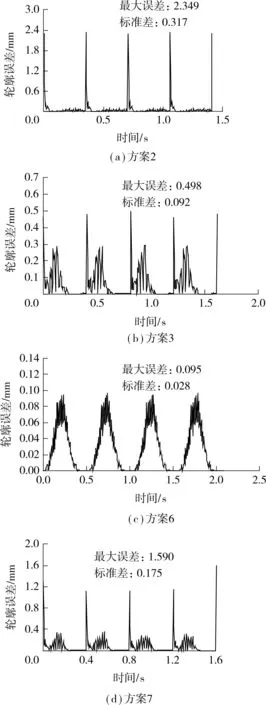
图3　轮廓误差分布对比Fig.3　Comparison of contour error distribution

文中所提方法以Pareto最优解集的形式给出一组备选的任务参数分配方案,设计人员可依据设计需求,灵活地选择最优数控实时任务参数.

4.2任务参数选择方法对比

为对比传统任务参数选择策略与所提方法的实际应用效果,以单调速率优先级分配方案(RMPA)为例,基于对比实验来分析不同方法间的性能差异.RMPA作为一种静态优先级分配策略,其依据任务周期的长短来确定调度优先级,周期越小的任务其优先级越高,反之优先级越低.以表1中第6组任务参数为例,依据RMPA,数控任务集的优先级分配方案为[4321].基于两组不同任务参数的对比实验结果如表2所示,表中自左至右分别给出了两组任务参数分配方案下的CPU使用率(CU)、加工时间(PT)、轮廓误差标准差(SD)以及最大轮廓误差(ME)的数据对比.由表2可知,与文中所提方法相比,RMPA分配方案下CPU使用率、加工时间无明显变化,但轮廓误差标准差和最大轮廓误差分别由0.028mm和0.095mm增加至0.040mm和0.259mm.在能耗和效率性能目标无明显变化的情况下,精度性能目标的下降直接影响数控系统整体性能.本实例的结果表明:文中所提方法具有更好的实际应用效果.

表2性能目标对比

Table 2Comparison of performance objectives

方法CU/%PT/sSD/mmME/mm文中方法20.192.0850.0280.095RMPA20.142.0800.0400.259

5结语

基于多目标优化的数控实时任务参数选择方法,是将任务参数的选择描述为一类多目标优化问题,结合ENSGA-II算法可在大规模决策空间下快速搜索数控系统整体性能目标最优的实时任务参数.由于工程应用中可能采取动态优先级调度等复杂的调度策略,如何提高所提方法的适用性是未来需要重点解决的问题.

参考文献：

[1]李迪,万加富,叶峰，等.软数控实时任务的时间特性对加工精度的影响 [J].华南理工大学学报(自然科学版),2009,37(2):1-6.

LIDi,WANJia-fu,YEFeng,etal.EffectoftimecharacteristicsofsoftwareNCreal-timetasksonmanufacturingaccuracy[J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition),2009,37(2):1-6.

[2]ARZENKarl-Erik,CERVINA,EKERJ,etal.Anintroductiontocontrolandschedulingco-design[C]∥Proceedingsofthe39thConferenceonDecisionandControl.Sydney:IEEE,2000:4865-4870.

[3]ARZENKarl-Erik,CERVINA.Controlandembeddedcomputing:surveyofresearchdirections[C]∥Proceedingsofthe16thIFACWorldCongress.Prague:Elsevier,2005:1072-1084.

[4]RipollI,Ballester-RipollR.Periodselectionforminimalhyperperiodinperiodictasksystems[J].IEEETransactionsonComputers,2013,62(9):1813-1822.

[5]CAOYu-nan.AformalspecificationframeworkfordesigningandverifyingreliableanddependablesoftwareforCNCsystems[J].AdvancesinMechanicalEngineering,2014,2014(8):1-22.

[6]XIAFeng,SUNYou-xian.Control-schedulingcodesign:aperspectiveonintegratingcontrolandcomputing[J].DynamicsofContinuous,DiscreteandImpulsiveSystems-SeriesB,2006,13(1):1352-1358.

[7]ZENGHai-bo,DINataleM.Anefficientformulationofthereal-timefeasibilityregionfordesignoptimization[J].IEEETransactionsonComputers,2013,62(4):644-661.

[8]CELAA,BENGaidM,LIXu-guang,etal.Optimaldesignofdistributedcontrolandembeddedsystems[M].Berlin:Springer,2014:47-66.

[9]WUYi-fan,BUTTAZZOG,BINIE,etal.Parameterselectionforreal-timecontrollersinresource-constrainedsystems[J].IEEETransactionsonIndustrialInforma-tics,2010,6(4):610-620.

[10]DUCheng-lie,TANLong-hua,DONGYa-li.Periodselectionforintegratedcontrollertasksincyberphysicalsystems[J].ChineseJournalofAeronautics,2015,28(3):894-902.

[11]AMINIFARA,ELESP,PENGZe-bo,etal.Stability-awareanalysisanddesignofembeddedcontrolsystems[C]∥ProceedingsoftheInternationalConferenceonofEmbeddedSoftware.Montreal:IEEE,2013:1-10.

[12]KORENY,CH-CHLo.Variable-gaincross-couplingcontrollerforcontouring[J].CIRPAnnals-ManufacturingTechnology,1991,40(1):371-374.

[13]DEBK,PRATAPA,AGARWALS,etal.Afastandelitistmulti-objectivegeneticalgorithm:NSGA-II[J].IEEETransactionsonEvolutionaryComputation,2002,6(2):182-197.

[14]ANTONIOLM,COELLOCOELLOCA.Useofcoopera-tivecoevolutionforsolvinglargescalemultiobjectiveoptimizationproblems[C]∥Proceedingsof2013IEEECongressonEvolutionaryComputation.Cancun:IEEE,2013:2758-2765.

[15]刘全,王晓燕,傅启明，等.双精英协同进化遗传算法[J]. 软件学报,2012,23(4):765-775.

LIUQuan,WANGXiao-Yan,FUQi-ming,etal.Doubleelitecoevolutionarygeneticalgorithm[J].JournalofSoftware,2012,23(4):765-775.

Parameter Selection of CNC Real-Time Task on the Basis of Multi-Objective Optimization

ZHAIZhen-kunLIDi

(School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China)

Abstract:In order to realize the parameter selection of CNC real-time task in collaborative design mode, a task parameter selection method on the basis of multi-objective optimization is proposed. In this method, a multi-objective optimization model is established according to real-time task model, performance objective as well as system constraint, and the model is solved by means of an extended non-dominated sorting genetic algorithm with co-evolution operator and elite team retention mechanism, thus the speed of searching optimal task parameters in large-scale decision space improves, which promotes the overall performance of CNC system to achieve the optimum. Finally, the parameter selection strategy of CNC real-time task is summarized according to simulation results and the superiority of the proposed method in practical application is proved through a comparison with the traditional task parameter selection approach.

Key words:numerical control systems; multi-objective optimization; real-time control; evolutionary computation

收稿日期：2015- 08- 04

*基金项目：国家科技支撑计划项目 (2015BAF20B01)；国家自然科学基金资助项目 (61262013)； 广东省科技计划项目 (2012A010702004，2012A090100012)

Foundation items: Supported by the National Key Technology Research and Development Program of the Ministry of Science and Techno-logy of China (2015BAF20B01) ,the National Natural Science Foundation of China (61262013) and the Science and Technology Planning Project of Guangdong Province,China (2012A010702004,2012A090100012)

作者简介：翟振坤(1984-),男,博士生,主要从事嵌入式系统设计原理与方法论、基于形式化方法的控制系统设计等研究.E-mail:smartzhai@163.com

中图分类号：TG502.35

doi：10.3969/j.issn.1000-565X.2016.03.004