一种基于信息熵的混合数据属性加权聚类算法

赵兴旺　　　梁吉业

(山西大学计算机与信息技术学院　太原　030006)(计算智能与中文信息处理教育部重点实验室(山西大学)　太原　030006)(zhaoxw84@163.com)

一种基于信息熵的混合数据属性加权聚类算法

赵兴旺梁吉业

(山西大学计算机与信息技术学院太原030006)(计算智能与中文信息处理教育部重点实验室(山西大学)太原030006)(zhaoxw84@163.com)

摘要同时兼具数值型和分类型属性的混合数据在实际应用中普通存在，混合数据的聚类分析越来越受到广泛的关注.为解决高维混合数据聚类中属性加权问题，提出了一种基于信息熵的混合数据属性加权聚类算法，以提升模式发现的效果.工作主要包括：首先为了更加准确客观地度量对象与类之间的差异性，设计了针对混合数据的扩展欧氏距离；然后，在信息熵框架下利用类内信息熵和类间信息熵给出了聚类结果中类内抱团性及一个类与其余类分离度的统一度量机制，并基于此给出了一种属性重要性度量方法，进而设计了一种基于信息熵的属性加权混合数据聚类算法.在10个UCI数据集上的实验结果表明，提出的算法在4种聚类评价指标下优于传统的属性未加权聚类算法和已有的属性加权聚类算法，并通过统计显著性检验表明本文提出算法的聚类结果与已有算法聚类结果具有显著差异性.

关键词聚类分析；混合数据；属性加权；信息熵；相异性度量

聚类分析的主要目的在于发现数据中隐含的类结构，将物理或抽象对象划分为不同的类，使得同一类内对象之间相似度较大，而不同类的对象之间相似度较小.作为一种主要的探索性数据分析工具，聚类分析目前已经在机器学习、数据挖掘、模式识别、生物信息学、统计学和社会计算等领域都得到了广泛的研究和应用[1].

半个多世纪以来，研究者针对不同的应用领域已经提出了诸多聚类算法，主要分为层次聚类算法和划分式聚类算法[2-4].其中，划分式聚类算法由于简单、高效、易实现等优点得到了广泛的应用.在传统的划分式聚类过程中，都假定各个属性对聚类的贡献程度相同，即在相似性或相异性度量的计算中所有属性的权重相同.而在大部分实际应用中，用户期望得到的聚类结果，对参与聚类的各个属性的重要程度往往并不相同.特别是在高维数据聚类过程中，样本空间中各属性对聚类效果贡献大小不同成为了一个不可回避的问题[5].因此，识别不同属性在聚类过程中的差异程度，从而提高聚类结果的质量，研究聚类过程中属性自动加权技术具有非常重要的意义.

近年来，为了计算不同属性对聚类贡献程度的差异性，许多学者针对聚类算法中属性加权问题已经开展了一些研究，提出了一系列属性自动加权聚类算法，这些研究大多针对数值型数据[6-8].然而现实生活中遇到的数据既可能是数值型数据，也可能是分类型数据，或同时由数值型和分类型属性共同描述的混合数据.与数值型数据相比，分类型数据的某一属性的取值是有限集合中的某一个值，而且取值之间没有序关系，这些特点使得分类型数据之间相似性度量的定义更为困难，从而使得数值型数据属性加权聚类算法无法直接应用于分类型数据[9-11].在分类型数据属性加权聚类算法方面，文献[10]提出了一种分类型数据属性加权聚类算法，在计算属性权重的过程中同时考虑了类中心出现的频率和类内对象到类中心平均距离.文献[11]提出了一个基于非模的分类型数据属性自动加权聚类方法，依据属性取值的总体分布情况对属性赋予不同权重.文献[12]设计了一种基于类内信息熵的分类型数据软子空间聚类算法，在每一个类中根据属性重要度对不同属性赋予不同的权重.

混合数据由于同时具有数值型属性和分类型属性，在对象之间相似性或相异性度量的定义和不同类型属性加权机制方面更为困难.其中，1998年，文献[13]通过把K-Modes算法和K-Means算法进行简单集成提出了针对混合数据的K-Prototypes算法.在该算法中，对象与类中心之间的相异性度量同时考虑了数值型数据和分类型数据，并通过参数来控制数值型部分和分类型部分贡献的大小.其中，在相异性度量方面，数值型属性之间的相异性度量采用欧氏距离，分类型属性之间的相异性通过简单0-1匹配来度量；在类中心表示方面，数值型数据部分采用均值(means)表示，而分类型数据分别采用众数(modes)表示.K-Prototypes算法由于简单易实现，已经在混合数据聚类中得到了广泛的应用.但是，欧氏距离和简单0-1匹配相异性度量的取值范围不同，而且不同类型数据之间的相异性度量仅仅通过一个参数进行调节，因此在聚类过程中不能客观地体现对象与类之间相异性在数值属性和分类属性各个属性的重要度.针对以上问题，一些学者已经进行了一些探索[14-16].如文献[14]针对分类数据部分，通过考虑同一属性下不同属性值的出现频率给出了一种新的相异性度量方法，并利用倒数比例计算法给出了一种新的类中心更新方式，通过与K-Means算法集成进而提出了一个可以处理混合数据的聚类算法.文献[15]给出了一个针对分类型和数值型属性统一的相似性度量方法，消除了不同类型数据之间度量量纲的差异性，同时也免去了不同度量之间参数的设置.该方法针对分类型数据，利用信息熵对不同分类属性的重要性进行了刻画.但是，在分类型属性加权过程中直接计算各个属性在所有数据上的信息熵，并没有考虑不同类之间的差异性；另外在计算相似性度量过程中把数值型数据的所有属性当作整体计算得到一个相似度度量的数值，然后与分类型属性部分进行加权，这种计算方法显然削弱了数值型数据部分的权重.

通过以上分析可知，已有的属性加权聚类算法主要存在3个局限性：

1) 大多数加权聚类方法仅仅针对数值型或分类型单一类型数据进行属性加权，这些方法在实际应用中存在一定的局限性；

2) 已有属性加权方法或者依赖于整体数据集属性值的总体分布情况(属性重要性与数据分布的离散程度成反比，数据集中某个属性的取值越集中，该属性的重要性就越高)，或者根据对象到类中心的距离定义的分散度来衡量(在某个类中某属性下的分散度越低，则该属性在该类的重要性越高)，而并没有考虑不同类之间属性值分布的差异性，这必然导致属性权重计算上的偏差，从而影响聚类质量；

3) 针对现实生活中广泛存在的混合型数据，已有方法在对象与类中心之间相似性或相异性度量方面，通常采用不同的度量机制，存在量纲不同的问题，不能客观地反映混合数据之间的差异性.

针对以上问题，本文基于信息熵理论提出了一个混合数据属性加权聚类算法.1)为了更加准确客观地度量对象与类之间的差异性，设计了一种针对混合数据的扩展欧氏距离；2)在信息熵框架下利用类内信息熵和类间信息熵给出了聚类结果中类内抱团性及一个类与其余类分离度的统一度量机制，并基于此给出了一种属性加权方法;3)在UCI数据集上实验结果表明，本文提出的属性加权聚类算法在4种评价指标下优于传统的未加权聚类算法和已有加权聚类算法.

1相关工作

本节主要对混合型数据聚类相关背景知识和K-Prototypes聚类算法进行介绍.

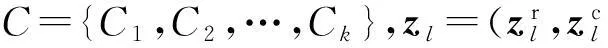
(1)

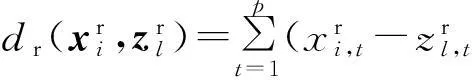
K-Prototypes算法最小化以下目标函数：

其中，wli∈{0,1},1≤l≤k,1≤i≤n；

wli=1时表示第i个对象属于第l个类，wli=0时表示第i个对象不属于第l个类.

为了使目标函数F在给定的约束条件下达到极小值，采用如下算法进行计算.

算法1.K-Prototypes聚类算法.

Step1. 从数据集X中随机选取k个对象作为初始类中心；

Step2. 根据式(1)计算对象与类中心之间的距离,并根据最近原则将每个对象分配到离它最近的类中；

Step3. 更新聚类中心，其中数值属性部分通过计算同一类中对象的平均值得到，分类型属性部分通过计算类中各属性值出现的频率高低来确定；

Step4. 重复Step2,Step3,直到目标函数F不再发生变化为止.

K-Prototypes算法由于简单、高效、易实现，已经得到了广泛的应用.但是，在相异性度量的定义中存在数值型数据和分类型数据部分量纲不同、参数γ难以确定、不能客观地反映对象与类中心的差异性的缺陷；而且在定义对象与类中心的差异性度量的过程中未考虑各个属性的重要性.本文在K-Prototypes算法的框架下，提出了一个针对混合数据迭代式的属性加权聚类算法.

2基于信息熵的混合数据属性加权聚类算法

在信息论中，信息熵是一种用于度量系统不确定性的度量方法.在一个系统中，某个属性取值的不确定性程度越大，表明系统越混乱，在该属性下系统的信息熵越大，它提供的信息量越小，该属性的重要性也就越小；反之，某个属性取值的不确定性程序越小，表明系统越有序，在该属性下信息熵越小，它提供的信息量越大，该属性的重要性也就越大.作为一种有效的度量机制，信息熵已经在聚类分析、孤立点检测、不确定性度量等领域得到了广泛的应用.本文根据各个属性下取值的不确定程度，利用类内和类间信息熵来度量各个属性在聚类过程中的重要程度.由于描述对象的属性类型不同，信息熵的计算方法也不同，本节将分别进行描述.

在给出数值型和分类型数据基于信息熵度量的属性加权机制之前，首先定义一种新的混合数据相异性度量方法.

2.1混合数据相异性度量方法

由于K-Prototypes算法中分类型数据部分的聚类中心仅仅将某类中当前属性值域中出现频率最高的取值(即modes)作为类中心，忽略了该属性的其余取值情况，而且往往会出现类中心不唯一的情况.本节首先给出分类型数据一种新的模糊类中心表示方式，并基于此将传统的欧氏距离扩展到混合数据，使得能够在统一的框架下更加客观地度量混合数据中对象与类之间的相异性.

定义1. 设Cl表示数据集X在聚类过程中得到的一个类，则分类型属性部分模糊类中心表示为

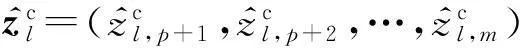
(2)

由定义1可知，数据集中的单一对象也可以表示为模糊类中心的形式，是模糊类中心表示的一种特殊形式.即针对某一属性下，当前对象的属性值对应的频率为1，其余值域对应的频率为0.

基于以上给出的分类型数据新的类中心表示方式，下面给出扩展的欧氏距离度量.

(3)

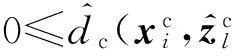
(4)

2.2基于信息熵的数值型属性加权机制

针对数值型数据，匈牙利数学家Renyi[17]于1961年提出了一个可以度量连续型随机变量的信息熵，称作Renyi熵.设连续型随机变量x的概率密度函数为f(x)，则该随机变量的Renyi熵定义为

(5)

当α=2，HR(x)=-ln∫f2(x)dx，记为二阶Renyi熵.

二阶Renyi熵由于计算方便、具有很好的性质，在实际应用中得到了广泛的应用.Parzen窗口估计法作为一种非参数估计方法，通常用于利用已知样本对总体样本的概率密度进行估计[18].因此二阶Renyi熵中的密度函数可以用Parzen窗口估计法来进行估计.设X={x1,x2,…,xN}，xi∈d，是一个由独立同分布的N个数据对象组成的数据集合，则对于任意随机变量x∈X利用Parzen窗口估计法估计出的概率密度为

(6)

其中，Wσ2表示Parzen窗函数，σ2表示窗宽.通常选取高斯核函数作为Parzen窗函数，即

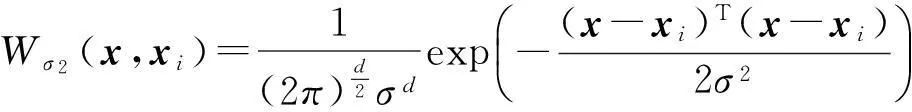
(7)

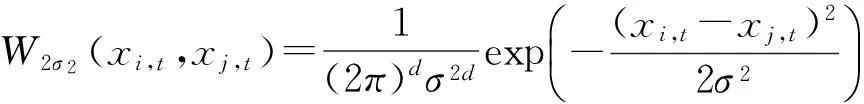
通过分析可知，基于Parzen窗口估计法得到的Renyi熵可能出现负值的情况.为了保证熵值为正及计算的方便，本文在W2σ2(xi,t,xj,t)之前乘以一个相对小的正数，即:

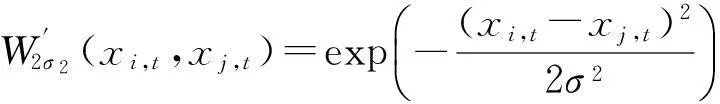
基于以上给出的Renyi熵，数值型数据在某一属性下类内熵、类间熵分别定义如下[20].

(8)

其中，Nk′=|Crk′|表示类Crk′中对象的个数.

上述定义给出的类内熵反映了聚类划分结果中某一类在不同的属性下数据分布的不确定程度.即在一个类中如果某个属性下的类内熵越小，则该属性在该类中的不确定性越小，聚类过程中该属性的权重就越大.

(9)

其中，Nk′=|Crk′|和Ns=|Crs|分别表示类Crk′和Crs中对象的个数.

基于定义4和定义5，下面给出数值型数据属性加权的定义.

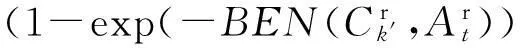
(10)

由定义6可知，属性权重与类内熵成反比，与类间熵成正比，而且类内熵、类间熵都已经归一化到[0,1]之间，因此，各个属性权重的范围为[0,1].由定义5可知，如果聚类个数为2时，类与类之间的平均类间熵则相等，此时属性权重只与类内熵有关.

2.3基于信息熵的分类型属性加权机制

针对分类型数据，文献[21]中提出了一个既可以用来度量随机性，又可以度量模糊性的互补信息熵.目前，该信息熵已经在不确定性度量、特征选择、聚类分析、孤立点检测等领域得到了广泛的应用[12,22-26].

基于互补熵，分类型数据的类内熵、类间熵分别定义如下[25]:

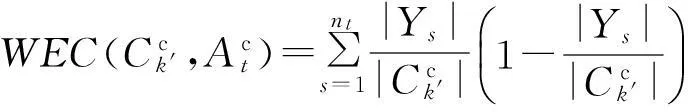
(11)

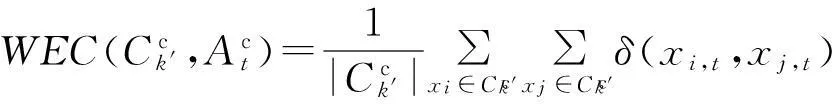
(12)

式(12)表明分类型数据类内熵与类内平均距离是等价的.因此，可以从距离的角度来定义分类型数据一个类与其余类之间的平均类间熵.

(13)

与数值型数据的信息熵类似，定义7和定义8给出的分类型数据的类内熵、类间熵分别表示在一个聚类划分结果中一个类在不同的属性下类内数据分布的不确定程度和与其余类的分离程度.

基于定义7和定义8，下面给出分类型数据属性加权的定义.

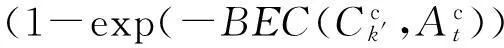
(14)

2.4基于信息熵的混合数据属性加权聚类算法

基于式(4)(10)(14)，任一对象xi∈X和类Cl(类中心表示为zl)的加权相异度度量定义为

(15)

由式(15)可知，在信息熵机制下结合类内信息熵和类间信息熵给出了针对数值型和分类型数据统一的加权方法，而且不同类型属性下的相异性度量的范围都在[0,1]之间，避免了量纲不同的问题，能够更加客观地反映混合数据中对象与类之间的差异性.

设X={x1,x2,…,xN}是一个混合型数据集，将上述给出的加权相异性度量应用到K-Prototypes算法框架中，算法的目标函数定义为

其中：

1≤l≤k,1≤i≤n；

以上优化问题是一个非常复杂的非线性规划问题，和K-Prototypes类型算法类似，采用逐步迭代优化的策略，即首先固定聚类中心Z，最小化目标函数F′得到隶属矩阵W；然后固定隶属矩阵W，最小化目标函数F′得到新的聚类中心Z；如此迭代，直到目标函数F′收敛为止.算法描述如下.

算法2. 基于信息熵的混合数据加权聚类算法.

输入: 数据集X={x1,x2,…,xN}、类个数k；

输出: 聚类结果.

Step1. 从数据集X中随机选取k个不同的对象作为初始聚类中心；

Step3. 根据式(15)计算对象与类中心之间的相异度，按照最近邻原则将数据对象划分到离它最近的聚类中心所代表的类中；

Step4. 更新聚类中心，其中数值属性部分通过计算同一类中对象取值的平均值得到，分类型属性部分根据定义1计算模糊类中心；

Step5. 根据定义6和定义9分别计算各个类在数值型和分类型数据部分各个属性的权重；

Step6. 重复Step3～Step5,直到目标函数F′不再发生变化为止.

3实验结果与分析

为了测试本文提出算法的有效性，我们从UCI真实数据集中分别选取了数值型、分类型和混合型3种不同类型的数据集进行了测试，并将本文提出的算法与K-Prototypes算法[13]、K-Centers算法[14]和基于属性加权的OCIL算法[15]、改进的K-Prototypes算法[16]进行了比较.10组数据集信息描述如表1所示，其中包括3个数值型数据、3个分类型数据和4个混合型数据.

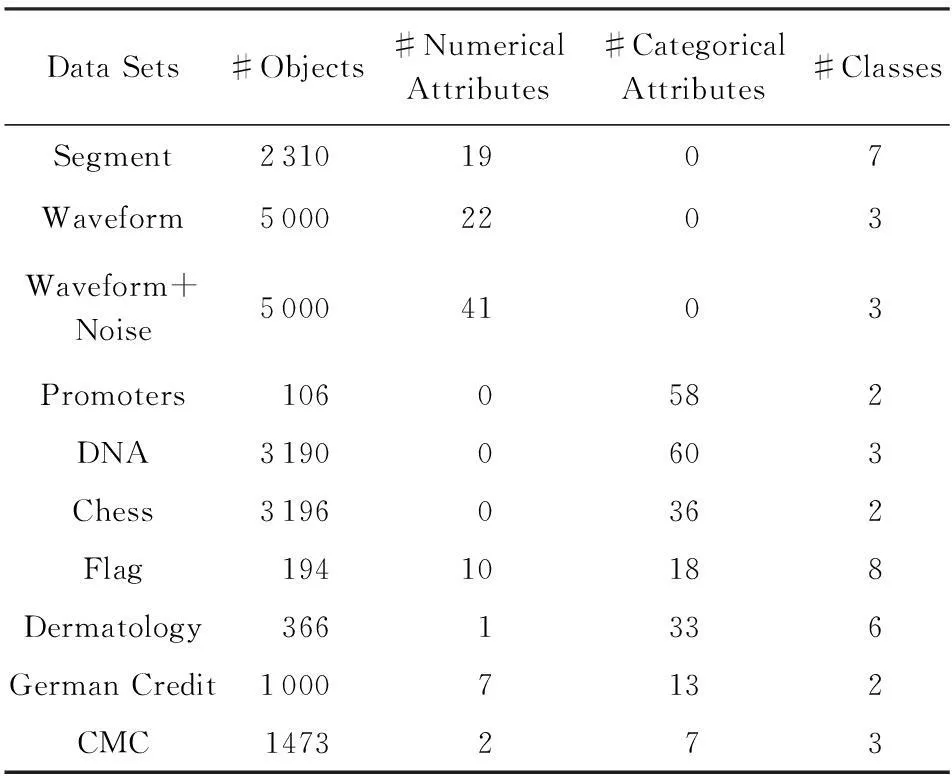
Table 1　The Summary of Data Sets’ Characteristics

为了对聚类结果的有效性进行评价，本文采用3个外部有效性评价指标和1个内部有效性评价指标对聚类结果评价.外部有效性评价指标包括聚类精度(clustering accuracy, CA)[14]、标准互信息(normalized mutual information, NMI)[27]和调整的兰特指数(adjusted rand index, ARI)[25]；内部有效性指标包括混合数据分类效用函数(category utility function for mixed data, CUM)[25].

实验中，由于本文提出的新算法和被比较算法的聚类结果均受初始类中心选择的影响，不同的初始类中心可能有不同的聚类结果.因此，以下实验结果均为算法随机运行50次评价指标的平均值和方差.K-Prototypes算法[13]、K-Centers算法[15]中的权重参数γ根据作者建议分别设置为γ=1.5和γ=0.5.改进的K-Prototypes算法[16]中参数λ根据作者建议设置为λ=8.另外，为了避免数值型不同属性间量纲的影响，在聚类之前对数值型数据进行了标准化处理.

3.1数值型数据聚类结果分析

在不同评价指标下，本文提出的新算法和其他4种聚类算法在数值型数据上聚类结果如表2～5所示.由于K-Prototypes算法、K-Centers算法和基于属性加权的OCIL算法在针对纯数值型数据聚类时，都退化为经典K-Means算法，因此本实验中针对数值型数据只将本文提出算法与K-Means算法、改进的K-Prototypes算法进行了比较.

Table 2Comparison of CA Values (means±std) of Different Algorithms on Numerical Data

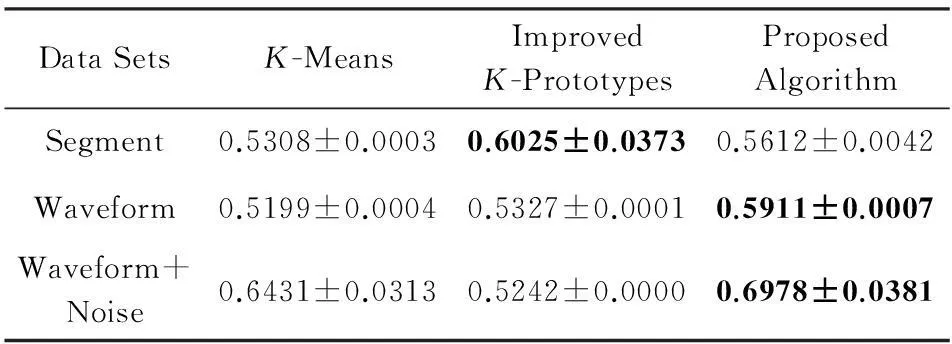
表2　数值型数据聚类结果比较：CA值(均值±方差)

Table 3Comparison of NMI Values (means±std) of

Different Algorithms on Numerical Data

表3　数值型数据聚类结果比较：NMI值(均值±方差)

Table 4Comparison of ARI Values (means±std) of

Different Algorithms on Numerical Data

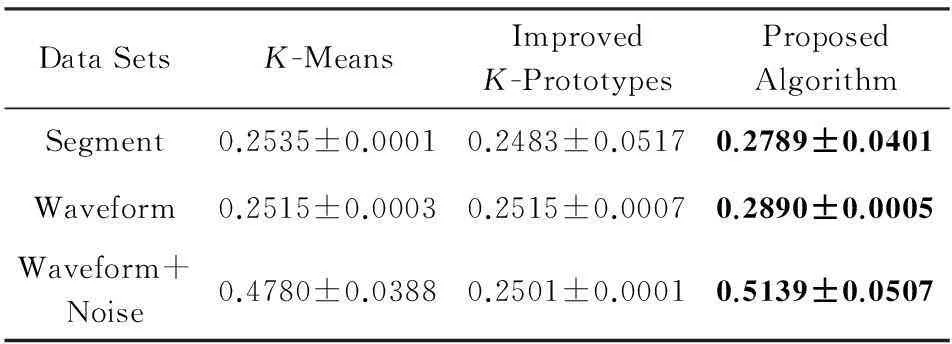
表4　数值型数据聚类结果比较：ARI值(均值±方差)

Table 5Comparison of CUM Values (means±std) of

Different Algorithms on Numerical Data

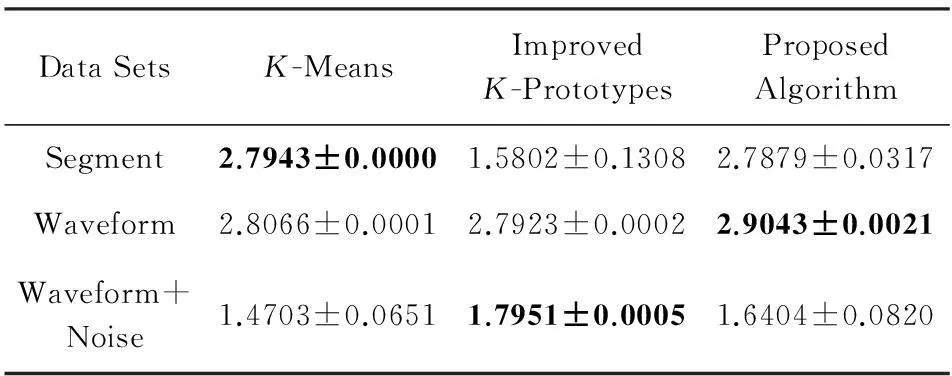
表5　数值型数据聚类结果比较：CUM值(均值±方差)

由表2～5可知，从CA，NMI，CUM指标看，本文提出的算法在Segment数据集上获得的聚类结果劣于其他算法，在CUM指标下本文算法在Waveform+Noise数据集上获得的聚类结果劣于改进的K-Prototypes算法.除此之外，在不同指标下本文提出的聚类算法在其他数据集上的聚类结果均优于其他算法.

3.2分类型数据聚类结果分析

在不同评价指标下，本文提出的新算法和其他4种聚类算法在分类型数据上聚类结果如表6～9所示:

Table 6　Comparison of CA Values (means±std) of Different Algorithms on Categorical Data

Table 7　Comparison of NMI Values (means±std) of Different Algorithms on Categorical Data

Table 8　Comparison of ARI Values (means±std) of Different Algorithms on Categorical Data

Table 9　Comparison of CUM Values (means±std) of Different Algorithms on Categorical Data

由表6～9可知，本文提出的算法除了在Chess数据集上聚类结果的CA值劣于改进的K-Prototypes算法之外，其余聚类结果均均优于其他算法.

3.3混合型数据聚类结果分析

在不同评价指标下，本文提出的新算法和其他4种聚类算法在混合数据上聚类结果如表10～13所示.

由表10～13可知，从CA和ARI评价指标看，K-Centers算法在Flag和German Credit数据集上取得了最优的聚类结果.除此之外，本文提出的算法在其余数据集上均取得了最优的聚类结果.

Table 10　Comparison of CA Values (means±std) of Different Algorithms on Mixed Data

Table 11　Comparison of NMI Values (means±std) of Different Algorithms on Mixed Data

Table 12　Comparison of ARI Values (means±std) of Different Algorithms on Mixed Data

Table 13　Comparison of CUM Values of (means±std) Algorithms on Mixed Data

3.4聚类结果统计显著性分析

针对本文提出算法的聚类结果与其他算法聚类结果差异是否显著的问题，本节利用无参数的Wilcoxon秩和检验方法进行了统计显著性检验.在不同评价指标下，将本文提出算法实验结果的均值分别与其余算法实验结果的均值进行了统计显著性检验.其中，原假设为在当前指标下本文算法与已有算法的聚类结果没有显著性差异，备择假设为不同聚类算法结果具有显著性差异.

置信区间为95%的Wilcoxon秩和检验结果h(p)如表14所示.其中数据分别表示假设检验结果h和p值.h=1表示在置信区间为95%时拒绝原假设接受备择假设，即表示本文提出算法的聚类结果与已有算法聚类结果具有显著差异性；h=0表示本文提出算法的聚类结果与已有算法聚类结果无显著差异性.由表14可知，本文提出算法在10个数据集获得的聚类结果在87.5%的情况下与其余聚类算法获得的聚类结果具有显著差异性.

Table 14Resultsh(p) of Wilcoxon Signed-ranks Test for the

Proposed Algorithm versus Other Algorithms

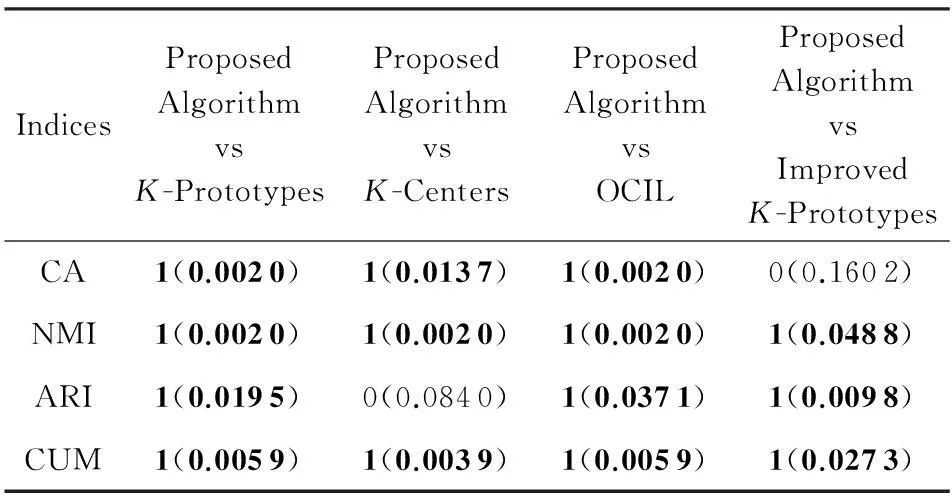
表14　本文算法与其余算法Wilcoxon秩和检验结果h(p)

4结束语

本文首先基于分类型数据类中心的模糊表示形式，给出了一种针对混合数据扩展的欧氏距离，能够更加客观准确地度量对象与类之间的差异性.其次，分别基于Renyi熵和互补熵定义了数值型数据和分类型数据的类内熵、类间熵，给出了属性加权机制，进而设计了一个基于信息熵的混合数据属性加权聚类算法.新提出的算法克服了主流聚类算法仅依据数据集总体分布或类内分散度进行属性加权的缺陷.在多个真实数据集上进行了实验验证，与其他混合数据聚类算法相比,本文提出的算法可以获得较高的聚类质量，而且与其他聚类结果具有显著差异性.

参考文献

[1]Han Jiawei, Kamber M, Pei Jian. Data Mining: Concepts and Techniques[M]. 3rd ed. San Francisco: Morgan Kaufmann, 2011

[2]Jain A K. Data clustering: 50 years beyondK-means[J]. Pattern Recognition Letters, 2010, 31(8): 651-666

[3]Xu Rui, Wunsch D. Survey of clustering algorithm[J]. IEEE Trans on Neural Networks, 2005, 16(3): 645-678

[4]Sun Jigui, Liu Jie, Zhao Lianyu. Clustering algorithms research[J]. Journal of Software, 2008, 19(1): 48-61 (in Chinese)(孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J]. 软件学报, 2008, 19(1): 48-61)

[5]Kriegel H P, Kröger P, Zimek A. Clustering high-dimensional data: A survey on subspace clustering, pattern-based clustering, and correlation clustering[J]. ACM Trans on Knowledge Discovery from Data, 2009, 3(1): 1-58

[6]Chan E Y, Ching W K, Ng M K, et al. An optimization algorithm for clustering using weighted dissimilarity measures[J]. Pattern Recognition, 2004, 37(5): 943-952

[7]Huang J Z, Ng M K, Rong Hongqiang, et al. Automated variable weighting ink-means type clustering[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2005, 27(5): 657-668

[8]Jing Liping, Ng M K, Huang J Z. An entropy weightingk-means algorithm for subspace clustering of high-dimensional sparse data[J]. IEEE Trans on Knowledge and Data Engineering, 2007, 19(8): 1026-1041

[9]Liang Jiye, Bai Liang, Cao Fuyuan.K-modes clustering algorithm based on a new distance measure[J]. Journal of Computer Research and Development, 2010, 47(10): 1749-1755 (in Chinese)(梁吉业, 白亮, 曹付元. 基于新的距离度量的K-modes聚类算法[J]. 计算机研究与发展, 2010, 47(10): 1749-1755)

[10]Bai Liang, Liang Jiye, Dang Chuangyin, et al. A novel attribute weighting algorithm for clustering high-dimensional categorical data[J]. Pattern Recognition, 2011, 44(12): 2843-2861

[11]Chen Lifei, Guo Gongde. Non-mode clustering of categorical data with attributes weighting[J]. Journal of Software, 2013, 24(11): 2628-2641 (in Chinese)(陈黎飞, 郭躬德. 属性加权的类属型数据非模聚类[J]. 软件学报, 2013, 24(11): 2628-2641)

[12]Cao Fuyuan, Liang Jiye, Li Deyu, et al. A weightingk-modes algorithm for subspace clustering of categorical data[J]. Neurocomputing, 2013, 108: 23-30

[13]Huang Zhexue. Extensions to thek-means algorithm for clustering large data sets with categorical values[J]. Data Mining and Knowledge Discovery, 1998, 2 (3): 283-304

[14]Zhao Weidong, Dai Weihui, Tang Chunbin.K-centers algorithm for clustering mixed type data[C]Proc of the 11th Pacific-Asia Conf on Knowledge Discovery and Data Mining. Berlin: Springer, 2007: 1140-1147

[15]Cheung Y, Jia Hong. Categorical-and-numerical-attribute data clustering based on a unified similarity metric without knowing cluster number[J]. Pattern Recognition, 2013, 46(8): 2228-2238

[16]Ji Jinchao, Bai Tian, Zhou Chunguang, et al. An improvedk-prototypes clustering algorithm for mixed numeric and categorical data[J]. Neurocomputing, 2013, 120: 590-596

[17]Renyi A. On measures of entropy and information[C]Proc of the 4th Berkley Symp on Mathematics of Statistics and Probability. Berkeley: University of California Press, 1961: 547-561

[18]Parzen E. On the estimation of a probability density function and the mode[J]. Annals of Mathematical Statistics, 1962, 33(3): 1065-1076

[19]Jenssen R, Eltoft T, Erdogmus D, et al. Some equivalences between kernel methods and information theoretic methods[J]. Journal of VLSI Signal Processing Systems, 2006, 45(12): 49-65

[20]Gokcay E, Principe J C. Information theoretic clustering[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2002, 24(2): 158-171

[21]Liang Jiye, Chin K S, Dang Chuangyin, et al. A new method for measuring uncertainty and fuzziness in rough set theory[J]. International Journal of General Systems, 2002, 31(4): 331-342

[22]Xu Weihua, Zhang Xiaoyan, Zhang Wenxiu. Knowledge granulation, knowledge entropy and knowledge uncertainty measure in ordered information systems[J]. Applied Soft Computing, 2009, 9(4): 1244-1251

[23]Wang Junhong, Liang Jiye, Qian Yuhua. Uncertainty measure of rough sets based on a knowledge granulation of incomplete information systems[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2008, 16(2): 233-244

[24]Qian Yuhua, Liang Jiye, Pedrycz W, et al. Positive approximation: An accelerator for attribute reduction in rough set theory[J]. Artificial Intelligence, 2010, 174(910): 597-618

[25]Liang Jiye, Zhao Xingwang, Li Deyu, et al. Determining the number of clusters using information entropy for mixed data[J]. Pattern Recognition, 2012, 45(6): 2251-2265

[26]Zhao Xingwang, Liang Jiye, Cao Fuyuan. A simple and effective outlier detection algorithm for categorical data[J]. International Journal of Machine Learning and Cybernetics, 2014, 5(3): 469-477

[27]Ienco D, Pensa R G, Meo R. From context to distance: Learning dissimilarity for categorical data clustering[J]. ACM Trans on Knowledge Discovery from Data, 2012, 6(1): 1-25

Zhao Xingwang, born in 1984. PhD candidate. Member of China Computer Federation. His main research interests include data mining and machine learning.

Liang Jiye, born in 1962. Professor and PhD supervisor. Distinguished member of China Computer Federation. His main research interests include granular computing, data mining and machine learning.

2014年《计算机研究与发展》高被引论文TOP10

数据来源：中国知网, CSCD；统计日期：2016-02-16

An Attribute Weighted Clustering Algorithm for Mixed Data Based on Information Entropy

Zhao Xingwang and Liang Jiye

(SchoolofComputerandInformationTechnology,ShanxiUniversity,Taiyuan030006)(KeyLaboratoryofComputationalIntelligenceandChineseInformationProcessing(ShanxiUniversity),MinistryofEducation,Taiyuan030006)

AbstractIn real applications, mixed data sets with both numerical attributes and categorical attributes at the same time are more common. Recently, clustering analysis for mixed data has attracted more and more attention. In order to solve the problem of attribute weighting for high-dimensional mixed data, this paper proposes an attribute weighted clustering algorithm for mixed data based on information entropy. The main work includes: an extended Euclidean distance is defined for mixed data, which can be used to measure the difference between the objects and clusters more accurately and objectively. And a generalized mechanism is presented to uniformly assess the compactness and separation of clusters based on within-cluster entropy and between-cluster entropy. Then a measure of the importance of attributes is given based on this mechanism. Furthermore, an attribute weighted clustering algorithm for mixed data based on information entropy is developed. The effectiveness of the proposed algorithm is demonstrated in comparison with the widely used state-of-the-art clustering algorithms for ten real life datasets from UCI. Finally, statistical test is conducted to show the superiority of the results produced by the proposed algorithm.

Key wordsclustering analysis; mixed data; attribute weighting; information entropy; dissimilarity measure

收稿日期：2015-02-12；修回日期：2015-06-09

基金项目：国家自然科学基金项目(61432011,U1435212,61402272)；国家“九七三”重点基础研究发展计划基金项目(2013CB329404)；山西省自然科学基金项目(2013021018-1)

通信作者：梁吉业(ljy@sxu.edu.cn)

中图法分类号TP391

This work was supported by the National Natural Science Foundation of China (61432011,U1435212,61402272), the National Basic Research Program of China (973 Program) (2013CB329404), and the Natural Science Foundation of Shanxi Province of China (2013021018-1).