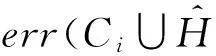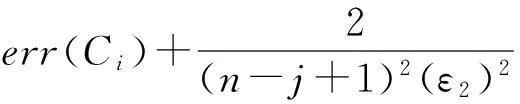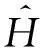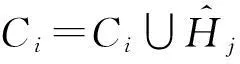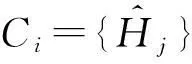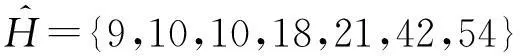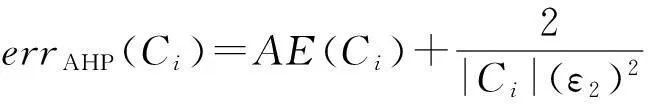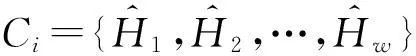差分隐私下一种精确直方图发布方法
2016-06-16张啸剑孟小峰
张啸剑 邵 超 孟小峰
1(河南财经政法大学计算机与信息工程学院 郑州 450002)2(中国人民大学信息学院 北京 100872)(xjzhang82@ruc.edu.cn)
差分隐私下一种精确直方图发布方法
张啸剑1邵超1孟小峰2
1(河南财经政法大学计算机与信息工程学院郑州450002)2(中国人民大学信息学院北京100872)(xjzhang82@ruc.edu.cn)
摘要基于分组的差分隐私直方图发布得到了研究者的广泛关注,组均值造成的近似误差与噪音造成的拉普拉斯误差之间的均衡直接制约着直方图发布精度.针对现有基于分组的直方图发布方法难以有效兼顾近似误差与拉普拉斯误差的不足,提出了一种满足差分隐私的精确直方图发布方法DiffHR(differentially private histogram release);通过分析直方图桶计数序列的排序有助于提升发布精度,利用Markov链蒙特卡洛(Markov chain Monte Carlo, MCMC)方法中的Metropolis-Hastings技术与指数机制,提出了一种有效排序方法,通过不断置换2个随机选取的桶以逐渐逼近正确排序;基于抽样排序后的直方图,提出了一种基于懒散分组下界的自适应贪心聚类方法,该方法的时间复杂度为O(n),并且可有效均衡近似误差与拉普拉斯误差.DiffHR,GS,AHP方法在真实数据上的实验结果表明,其发布精度上优于同类算法.
关键词差分隐私;直方图发布;分组;拉普拉斯误差;近似误差
快速而又准确地获取数据分布的梗概是数据分析与查询的主要任务.直方图是近似估计数据分布的主要技术之一,该技术使用分箱技术近似描述数据分布信息,将数据集按照某种属性划分成不相交的桶,每个桶由频度或者计数表示其特征.直方图的发布通常用来支持聚集查询、范围计数查询以及数据挖掘等应用.然而,如果直接发布直方图而不给予隐私保护,桶的真实计数会泄露个人的敏感信息.图1为HIV疾病监控中心确诊患者的年龄分布,其中40岁患者为20人.如果攻击者知道了除Alice之外其他19人的年龄情况,攻击者利用图1中的直方图可以推理出Alice患了HIV疾病,进而泄露了Alice的个人隐私.
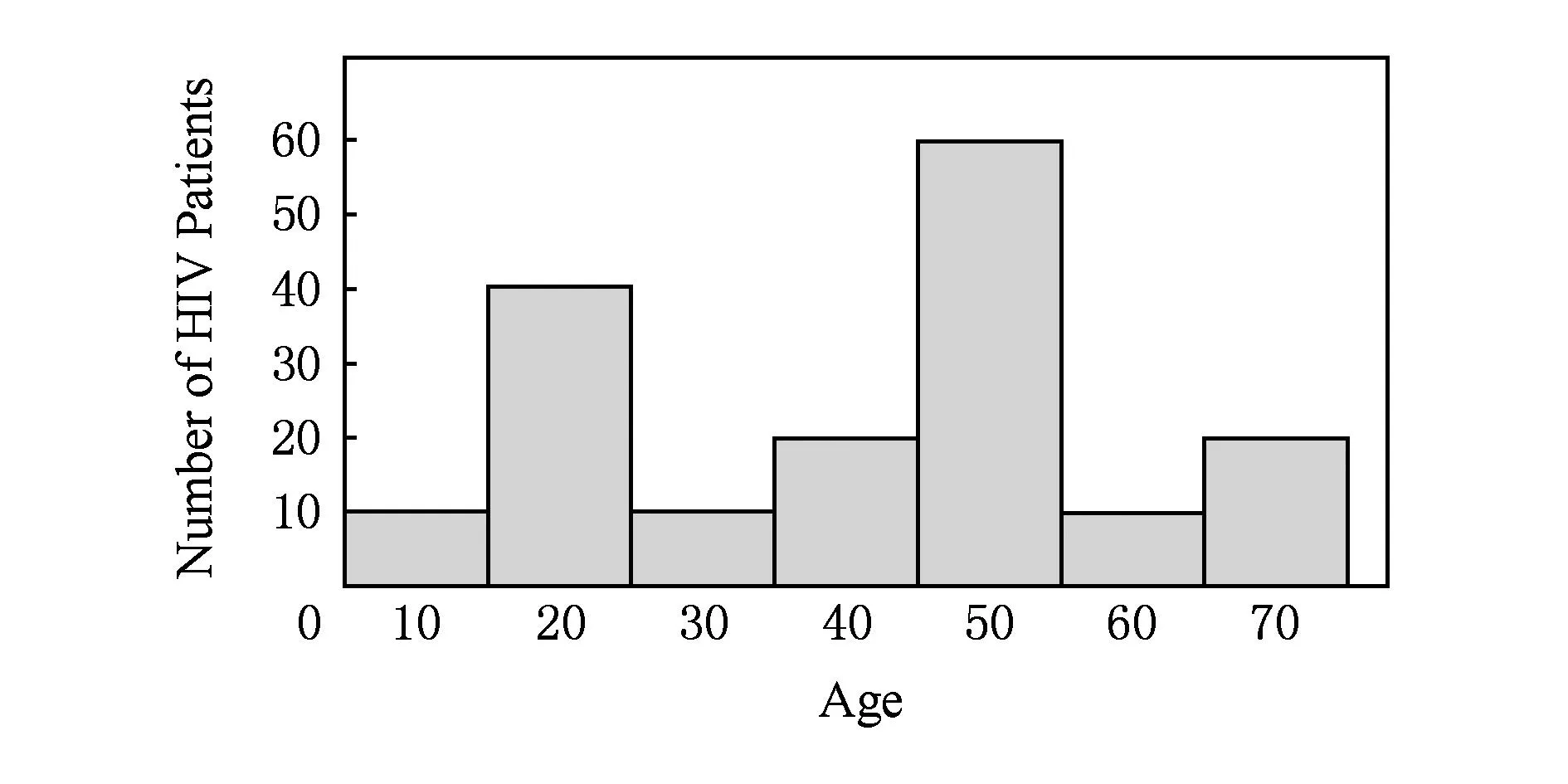
Fig. 1 Original histogram under age.图1 年龄分布下的原始直方图
为了阻止直方图统计信息带来的隐私泄露,在发布之前,需要对其进行隐私保护处理.目前差分隐私[1-4]已经成为一种新的隐私保护模型,基于该模型出现了多种直方图发布方法.其中,基于数据相关(data dependent)的分组方法是差分隐私下直方图发布的主要技术,该技术利用组平均值近似估计每个原始计数,例如图2给出图1的3个分组结果{C1,C2,C3},其中C1的{10,40,10}计数被其均值20代替.分组操作的优点在于能够比较准确地响应范围查询.然而,由于均值与拉普拉斯机制实现隐私保护,不可避免地产生均值造成的近似误差与拉普拉斯噪音造成的拉普拉斯误差.文献[5-9]描述了目前基于分组的差分隐私直方图发布常用方法,这些方法通常在固定分组个数的基础上利用有损压缩、V-优化直方图以及等宽划分技术减少误差对发布结果的影响,然而这些方法存在3个问题.
1) 分组时只是考虑局部近邻的桶计数(例如文献[5-7]),而无法度量全局计数的近邻关系,这种类型的分组无法均衡近似误差与拉普拉斯误差,导致所发布直方图的精度比较低.例如,在图1直方图中,尽管桶10与桶30的计数值一样,它们不能被单独放在一个分组中,除非桶20也被放在该分组中.这通常会导致很大的近似误差.
2) 分组时大都未考虑桶计数的全局顺序性,进而无法聚集全局相似的计数.例如,如果对图1直方图进行排序,则桶10,30,60由于计数值相同而被分到同一组,进而可以减少近似误差带来的影响.虽然文献[8]采用了排序,但是其采取固定分组策略却很难均衡近似误差与拉普拉斯误差;同样文献[9]采用简单的噪音排序也会导致不准确的结果.
3) 文献[5-9]中分组方法的时间复杂度大都是O(kn2)或者O(n2),例如AHP,GS方法.然而当直方图维度很大时,这些方法的分组效率比较低.
总而言之,目前还没有一个行之有效的方法兼顾直方图发布的近似误差与拉普拉斯误差.为此,本文提出了一种融合抽样排序与全局化分组的方法DiffHR(differentially private histogram release),在满足差分隐私的情况下,采用Metropolis-Hastings技术对直方图进行抽样处理,并实施自适应贪心聚类,实现近似误差与拉普拉斯之间的均衡.
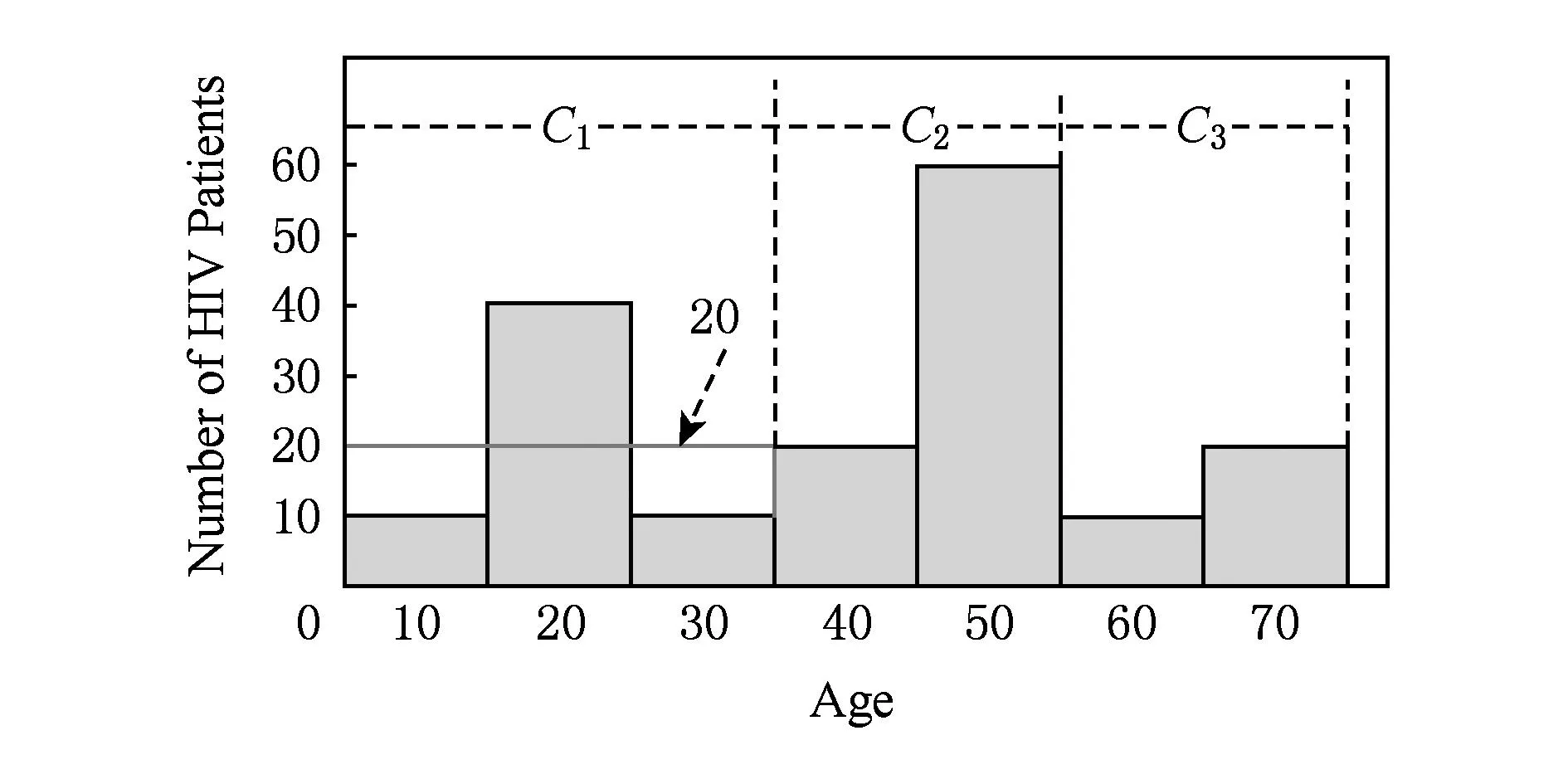
Fig. 2 Histogram after grouping.图2 分组后的直方图
本文主要贡献如下:
1) 为了精确发布直方图,提出了一种满足ε-差分隐私的方法DiffHR,该方法利用基于Markov链蒙特卡洛(Markov chain Monte Carlo, MCMC)方法中Metropolis-Hastings技术与指数机制对直方图进行抽样处理,通过不断置换2个随机选取的桶以逼近直方图的正确排序;
2) 为了有效均衡近似误差与拉普拉斯误差,提出了一种自适应的贪心聚类方法,该方法在满足差分隐私的前提下,采用懒散分组下界有效处理大维度直方图发布,且其时间复杂度为O(n);
3) 理论分析了DiffHR方法满足ε-差分隐私,通过真实数据集上的实验分析展示该方法在兼顾高可用性和准确性的同时,优于同类方法.
1相关工作
差分隐私拥有极强的保护能力和依赖严谨的统计模型,这些特点使其得到广泛研究和应用.当前学术界的应用着重关注差分隐私保护下的计数查询[10]、直方图发布[5]、子图查询[11]、高维数据发布[12]、关联数据查询发布[13]、机器学习[14]与数据挖掘[15]等.鉴于直方图在数据分析中的重要性,研究者已经提出了大量基于差分隐私的直方图发布方法.Dwork等人[1]提出了拉普拉斯机制,成为后续研究的基石.Xiao等人[16]提出了名为Privelet的基于小波的直方图发布技术.Privelet首先对输入数据进行小波变换,然后对变换后的频域数据添加多重对数噪声.Hay等人[17]指出约束推理可以作为一种后置处理方法来改善直方图的查询准确性.Li等人[10]提出了矩阵机制.给定一组查询,矩阵机制首先生成另外一组被称为查询策略的查询,并在其之上添加拉普拉斯噪音,最后通过查询策略的加噪结果来估算给定查询的值.Rastogi和Nath[18]指出静态时间序列数据可以通过只保留前k个傅里叶系数来以较小的近似误差换取较大的拉普拉斯噪音降幅.2012年Yuan等人[19]提出了低秩机制,它通过计算给定负荷矩阵的低秩近似来回答批次查询.上述方法大都属于数据无关(data independent)的方法,优势在于能够给出严谨的数据效用理论下限;但在实际数据上,这一系列方法均无法获得理想数据可用性和效率,这一缺点引出了数据相关方法的研究.
所有数据相关的研究中最有希望的当属基于分组的方法.Xu等人[5]提出了NoiseFirst和Structure-First算法.对于给定的分组个数,NoiseFirst先对每个桶添加独立拉普拉斯噪音,之后利用V-优化直方图构造方法在加噪后的直方图上寻找分组;StructureFirst则通过不断应用指数机制来确定不同组之间的分界.文献[5]主要缺陷在于只考虑相对于非隐私的V-优化直方图的近似误差,而忽略了拉普拉斯噪音带来的误差,此外其要求分组数目已知的假设也通常难以满足.Acs等人[6]改进了文献[5]中要求给定分组个数的缺陷,设计了一种分级的二分法算法,利用指数机制动态确定分组,并通过大量实验证实基于分组的方法可以取得比数据无关方法更好的准确性.应该指出,分组仅仅提供“本地化”的聚类,通常无法找到最优聚类,故而无法找到近似误差和拉普拉斯误差间的最佳平衡来最小化整体误差.Li等人[7]提出了一种基于分组策略的直方图方法DAWA,然而,该方法同样没有采用排序和“全局化”聚类方法.Kellaris等人[8]考虑一个稍微不同的问题设置:一个用户可以重复出现在多个桶中.他们首先利用采样方法对直方图进行排序,然后将所有桶分成大小相同的组.然而,选取固定的组大小通常无法很好地平衡近似误差和拉普拉斯误差,从而直接影响最终的发布精度.Zhang等人[9]提出了一种全局化聚类方法AHP,该方法取得了比文献[5-8]中较好的发布结果;然而,AHP在进行排序时,只是采用简单的噪音处理方式,而这种方式通常导致不准确的排序结果.因此,本文针对上述数据相关方法存在的缺陷,提出了一种精确直方图方法DiffHR来均衡近似误差和拉普拉斯误差.
2定义与理论基础
2.1差分隐私
差分隐私要求数据库中任何一个用户的存在都不应显著地改变任何查询的结果,从而保证了每个用户加入该数据库不会对其隐私造成危险.传统的隐私保护模型如k-anonymity[20],l-diversity[21]等通常对攻击背景知识与攻击模型给出特定的假设,而现实中这些假设并不成立.相比于传统保护模型,差分隐私保护模型具有2个显著的特点:1)不依赖于攻击者的背景知识;2)具有严谨的统计学模型,能够提供可量化的隐私保证.本文所关心的是在发布直方图时,如何使得所发布直方图满足差分隐私.
定义1. 设H={H1,H2,…,Hn}为原始直方图桶计数序列,其中Hi表示第i个桶的计数.H′={H1,H2,…,Hr-1,Hr±1,Hr+1,…,Hn},H与H′相差一个计数,则二者互为近邻关系.
结合H与H′给出ε-差分隐私的形式化定义,如定义2所示:
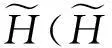
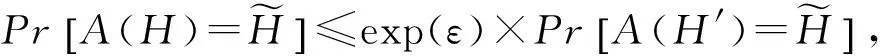
(1)
其中,ε表示隐私预算,其值越小则算法A的隐私保护程度越高.
从定义2可以看出ε-差分隐私限制了任意一个记录对算法A输出结果的影响.实现差分隐私保护需要噪音机制的介入,拉普拉斯与指数机制是实现差分隐私的主要技术.而所需要的噪音大小与其响应查询函数f的全局敏感性密切相关.
定义3. 设f为某一个查询,且f:H→d,f的全局敏感性为
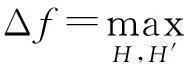
(2)
文献[1]提出的拉普拉斯机制可以取得差分隐私保护效果,该机制利用拉普拉斯分布产生噪音,进而使得发布方法满足ε-差异隐私,如定理1所示.
定理1[1].设f某一个查询函数,且f:H→d,若方法A符合式(3),则A满足ε-差分隐私.
(3)
其中,Lap(Δfε)为相互独立的拉普拉斯噪音变量,噪音量大小与Δf成正比,与ε成反比.因此,查询f的全局敏感性越大,所需的噪音越多.
文献[22]提出的指数机制主要处理抽样算法的输出为非数值型的结果.该机制的关键技术是如何设计打分函数u(H,Hi).设A为指数机制下的某个隐私方法,则A在打分函数作用下的输出结果为
A(H,Hi)=
(4)
其中,Δu为打分函数u(H,Hi)的全局敏感性,H为采用算法的输出域.由式(4)可知,Hi的打分函数越高,被选择输出的概率越大.
定理2[22].对于任意一个指数机制下的算法A,若A满足式(4),则A满足ε-差分隐私.
2.2直方图发布误差
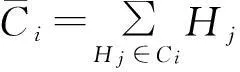
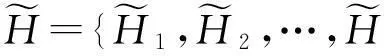
(5)
其中,LE(Ci)为采用拉普拉斯分布的方差度量,AE(Ci)为采用和方差度量.LE(Ci)与AE(Ci)可表示为
LE(Ci)=2(Δfε)2.
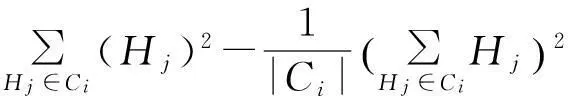
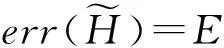
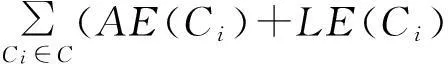
(6)
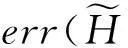
3差分隐私下精确直方图发布方法
3.1基于分组的原则
基于第1节相关工作分析,在设计新的基于分组的直方图发布方法时需要考虑的基本原则包括:
1) 针对全局分组问题,算法需要在满足差分隐私的条件下尽量把全局相似的计数值分到一组;
2) 针对近似误差与拉普拉斯误差之间的均衡问题,方法应从“全局化”自适应分组出发.
若实现原则1,最直接有效的方法是对H进行排序,这样相似的计数均会紧密排列.然而,如果直接基于H进行排序后分组,则会破坏ε-差分隐私[8].如何在满足差分隐私下准确排序是本文的第一研究难点.最简单的方法是对直方图每个桶添加独立的拉普拉斯噪音,根据加噪的计数值排序[8-9],然而此方法会导致不准确的排序.因此,本文采用Metropolis-Hastings抽样技术[23]与指数机制使全局相似的计数值尽可能分到同一个组;针对原则2,在不给定组个数以及不固定组大小的情况下,本文设计了一种自适应地贪心聚类分组方法.基于上述分析,提出了兼顾上述2种原则的直方图发布方法DiffHR,如算法1所示.
3.2DiffHR方法实现
DiffHR方法的具体描述如下:
算法1. DiffHR方法.
输入:直方图H={H1,H2,…,Hn}、隐私预算ε;
①ε=ε1+ε2;
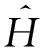
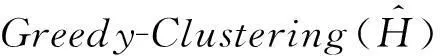
④ fori=1 tondo
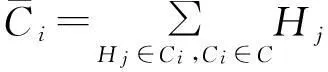
⑥ end for
⑦ fori=1 tondo
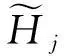
⑨ end for
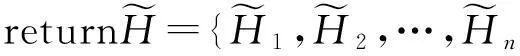
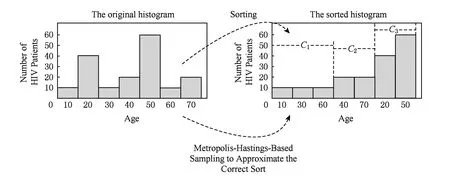
Fig. 3 Sorted-based histogram after grouping.图3 基于排序分组后的直方图
该方法包括2个主要步骤:Metropolis-Hastings抽样技术与贪心聚类.给定一个原始直方图计数序列H,给定部分隐私预算ε1,利用Metropolis-Hastings抽样技术与指数机制对H进行排序处理(行②);而算法的关键步骤是抽样处理后的聚类操作(行③),其目的是为了降低每个分组本身的误差err(Ci);最后,求每个簇的均值,利用剩余的隐私预算ε2为各个均值添加拉普拉斯噪音(行④~⑨).
为了深入理解DiffHR方法在分组过程中所引入的误差,给出以下定理.
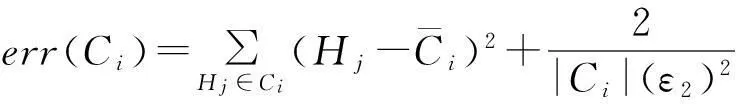
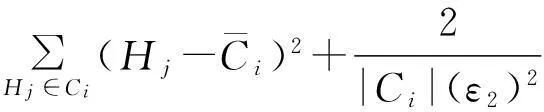
证毕.
3.2.1抽样处理方法Metropolis-Hastings-Sort
基于排序后的直方图进行分组操作,则可以把全局性相似的桶计数分到同一个组中,如图3右图所示,分组C1中3个桶{10,30,60}的计数为10且均值为10,分组C2中2个桶{40,70}的计数为20且均值为20,进而使得分组C1与C2的近似误差为0.
然而,如果直接基于原始直方图H中真实桶计数进行排序(例如图3右图所示),会导致个人隐私泄露.因此,本文通过MCMC把直方图H模拟成Markov链,然后利用基于指数机制的Metropolis-Hastings抽样技术来近似逼近H的正确排序.
1) 基于指数机制的Metropolis-Hastings抽样技术
根据指数机制的定义可知,直方图中任意一个桶被抽样的概率可以表示为
(7)
为了采用MCMC中的Metropolis-Hastings抽样技术,首先给出相关描述信息.
定义4. 给定一个Markov链{Xt:t=0,1,…},则其定义为
P(Xt+1=Hj|Xt=Hi,Xt-1=Hi-1,…)=
P(Xt+1=Hj|Xt=Hi).
该定义说明下一个状态只取决于当前的状态.
设X为一个随机变量,其在状态空间H={H1,H2,…,H|H|}中进行取值.Metropolis-Hastings方法根据Markov链定义在空间H中抽样出一个不可约的、非周期的Markov链,并使其服从平稳概率分布π(X).基于Metropolis-Hastings的Markov链构造过程,实际上是状态空间的转换过程,而状态转换由转换概率P决定.
P(Hi,Hj)=P(Xt+1=Hj|Xt=Hi)=
(8)
其中,Q(Hi,Hj)为建议概率分布,αHiHj表示接受概率,即表示状态Hi以概率αHiHj跳转到状态Hj,以(1-αHiHj)的概率保持原来状态.
(9)
采用式(7)中的π(Hi)代替接收概率式(9)中的π(Hi),则αHiHj重新表述为
(10)
根据式(10)可知,剩余的2个问题分别是如何设计打分函数u(H,Hj)与建议概率分布Q(Hi,Hj).
打分函数u(H,Hj)在指数机制中至关重要,我们希望那些打分高的桶计数被抽样出来.给定直方图H与当前状态Hi,采用抽样状态Hj与当前状态Hi的距离作为打分函数,如式(11)所示:

(11)
根据式(7)与式(11)可知,距离当前状态Hi越近的桶计数越容易被Metropolis-Hastings方法抽样.u(H,Hj)的敏感度为1,因为改变H的桶中任意一个计数,最多影响u(H,Hj)的变化为1.
同样,构造一个合理的建议概率分布Q(Hi,Hj)对Metropolis-Hastings抽样效果也至关重要.因此,根据不同状态之间的距离来设计Q(Hi,Hj).给定一个距离阈值θ(实验中设置θ=50),可以求出与当前状态Hi近邻的状态集合S1(Hi)={Hj:||Hj-Hi|≤θ}.假设S1(Hi)中的状态是被等概率抽样,则Q(Hi,Hj)=1S1(Hi).若Hi的距离不满足θ的状态称之为Hi的非近邻状态,该集合为S2(Hi)={Hj:||Hj-Hi|>θ}.同理,Q(Hi,Hj)=1S2(Hi).
2) Metropolis-Hastings-Sort算法
基于上述分析,给出Metropolis-Hastings-Sort方法的具体实现细节.
算法2. Metropolis-Hastings-Sort算法.
输入:直方图H={H1,H2,…,Hn}、隐私预算ε1;
① fori=1 tondo
② 随机选择一个桶计数作为种子计数;
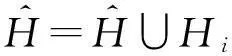
④ 根据阈值θ,计算从当前桶计数Hi到近邻桶Hj的跳转概率Q(Hi,Hj);
⑤ 以接收概率αHiHj接收桶Hj,其中αHiHj如式(10)所示;
⑥ if抽样Markov链收敛到π(X) then
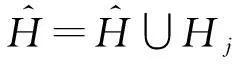
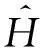
⑨ end if
⑩ end for
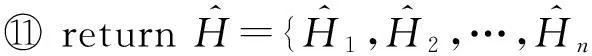
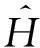
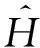
3.2.2基于懒散分组下界的方法Greedy-Clustering
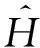
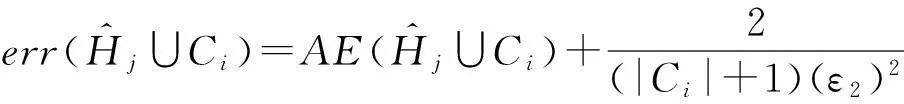
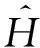
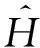
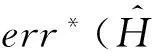
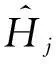
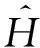
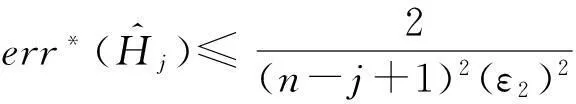
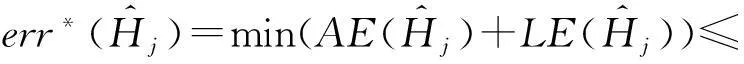
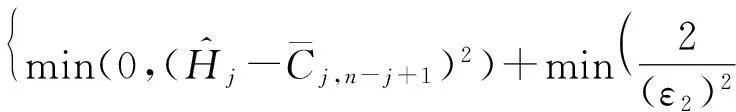
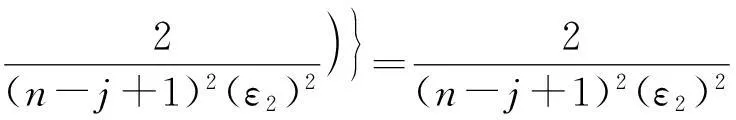
证毕.
根据上述分析,给出Greedy-Clustering方法的具体实现细节,如算法3所示.
算法3. Greedy-Clustering算法.
输出:聚类后所得分组集合C.
①C=∅;
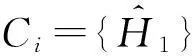
③ whilej ⑧ else ⑨C=∪Ci; 4隐私性与可用性分析 算法的隐私性主要从ε-差分隐私的概念和性质的角度来证明,而可用性主要是利用最终的发布误差进行度量.本节主要论证DiffHR是否满足ε-差分隐私,并在算法3的基础上与AHP以及GS算法进行可用性对比分析 4.1隐私分析 定理5. DiffHR满足ε-差分隐私. 证明. 在DiffHR方法中,行②利用指数机制对原始直方图H进行Metropolis-Hastings抽样.相当于n个查询,这n个查询记为Q1.根据定义3可知,删除原始H一条记录,最多影响H中一个桶的计数,则ΔQ1=1,根据定理2可知行②满足ε1-差分隐私.行⑦利用拉普拉斯机制计算每个组的噪音均值.由于每个组的大小已知,相当于查询每个组的计数总和,即是查询SUM值,该类查询记为Q2.同理ΔQ2=1.根据定理1可知,行⑧满足ε2-差分隐私.根据定理6差分隐私的顺序组合性质可知,DiffHR满足(ε1+ε2)-差分隐私.由于ε=ε1+ε2,则DiffHR满足ε-差分隐私. 证毕. 4.2可用性分析 可用性是度量隐私算法的另外一个标准,采用发布误差进行度量.DiffHR方法发布直方图的最终误差由总体的近似误差与总体的拉普拉斯误差构成.接下来比较DiffHR与AHP以及GS所发布直方图的可用性和准确性.DiffHR方法主要是基于懒散分组下界的聚类划分方法进行与其他2种方法进行比较. 1) DiffHR方法与AHP方法比较 2) DiffHR方法与GS方法比较 尽管GS算法也是采用排序与全局化分组策略,但是该方法采用固定宽度划分可能会导致发布准确性比较低.定理7可以解释固定宽度划分存在的缺陷.设GS等宽划分宽度为w. 因此,根据定理7可知,GS方法在固定宽度划分下所形成的组,总能够分裂成2个非均匀的误差较小的子组.相反,DiffHR却能够自适应地找出这些大小不一的子组,并使得最终发布误差最小. 5实验结果与分析 实验所采用的3个数据集Waitakere[8],Nettrace[10],Search_log[5]被广泛使用于直方图发布.其中Waitakere是新西兰2006年的人口街区普查数据,抽取7725街区作为直方图的桶;Search_log合成了2004~2010年Google Trends与American Online搜索关键字为“奥巴马”的搜索日志,该数据集包含32 768条记录;Nettrace源自于一所高校内联网的IP层网络轨迹数据,包含65 535条记录桶,每个桶记录校外主机链接校内某个主机个数. 结合上述3种数据集,采用均方误差(MSE)度量DiffHR,GS以及AHP方法发布直方图的准确性与可用性.设置隐私预算参数ε分别为0.01,0.10,1.00. 1) 直接添加拉普拉斯噪音与DiffHR方法处理对比 Fig. 4 Original histogram and Laplace noise.图4 原始直方图与拉普拉斯噪音 Fig. 5 Original histogram and DiffHR noise.图5 原始直方图与DiffHR噪音 针对上述3个数据集,设ε=0.01,直接对3种数据集添加拉普拉斯噪音,结果如图4所示.其中灰色表示拉普拉斯噪音,黑色表示3种数据集中直方图的真实计数.可以看出,拉普拉斯噪音几乎覆盖了真实的计数值,因此,直接在直方图上添加拉普拉斯噪音,其可用性很低,并且不能较好地响应范围计数查询.图5中灰色为基于DiffHR方法产生的噪音,黑色同样为3种数据集上的真实计数.可以看出DiffHR方法对真实直方图的扰动远低于拉普拉斯机制,特别是在Search_logs与Nettrace有序的数据集上,DiffHR方法的噪音影响更小. 2) DiffHR与GS以及AHP的均方差(mean squared error,MSE)值对比通过改变范围查询的大小以及结合不同的隐私预算参数ε值来对比DiffHR,GS以及AHP方法响应范围查询的结果准确性.进而比较这3种算法所发布直方图的可用性.由图6~8可以发现,范围查询的MSE值越小表示发布直方图的可用性越高.随着范围查询大小的增加,以及参数ε从0.01变化到1.00,DiffHR,GS以及AHP方法的MSE值也在相应增加,其原因是大的查询范围以及小的ε值造成拉普拉斯噪音的累积,进而增加拉普拉斯误差.对比着其他2种算法,DiffHR响应3种数据集上的范围查询时所造成的MSE比较小.特别是在Waitakere与Search_log数据集上,DiffHR所取得的范围查询响应精度是GS方法的将近10倍,是AHP方法的将近3倍.虽然在Nettrace数据集上,DiffHR方法与AHP方法取得近似的均方误差,但是DiffHR方法仍然优于AHP方法,原因是DiffHR方法采用了比AHP方法更准确的排序策略. Fig. 6 MSE on Waitakere under different ε values (y-axis is in log-scale).图6 Waitakere下ε变化时MSE的变化 Fig. 7 MSE on Search_logs under different ε values (y-axis is in log-scale).图7 Search_logs下ε变化时MSE的变化 Fig. 8 MSE on Nettrace under different ε values (y-axis is in log-scale).图8 Nettrace下ε变化时MSE的变化 6结束语 针对差分隐私行下基于分组的直方图发布问题,本文首先对现有基于分组发布进行分析,并在此基础上提出基于聚类分组算法DiffHR,引入满足差分隐私的Metropolis-Hastings抽样技术进行逼近直方图正确排序.在排序的基础上提出了一种基于懒散分组的聚类方法.从理论角度进行对比分析的结果显示,DiffHR优于同类算法.最后,通过真实数据集的实验结果表明DiffHR能够在满足差分隐私的同时输出比较精确的直方图.未来工作考虑数据流下发布直方图,设计满足数据流特点的分组发布策略. 参考文献 [1]Dwork C, McSherry F, Nissim K, et al. Calibrating noise to sensitivity in private data analysis[C]Proc of the 3rd Theory of Cryptography Conf (TCC 2006). Berlin: Springer, 2006: 363-385 [2]Dwork C. Differential privacy[C]Proc of the 33rd Int Colloquium on Automata, Languages and Programming (ICALP 2009). Berlin: Springer, 2006: 1-12 [3]Dwork C, Lei J. Differential privacy and robust statistics[C]Proc of the 41st Annual ACM Symp on Theory of Computing (STOC 2009). New York: ACM, 2009: 371-380 [4]Dwork C, Naor M, Reingold O, et al. On the complexity of differentially private data release: Efficient algorithms and hardness results[C]Proc of the 41st Annual ACM Symp on Theory of Computing (STOC 2009). New York: ACM, 2009: 381-390 [5]Xu J, Zhang Z, Xiao X, et al. Differential private histogram publication[J]. The VLDB Journal, 2013, 22(6): 797-822 [6]Acs G, Chen R. Differentially private histogram publishing through lossy compression[C]Proc of the 11th IEEE Int Conf on Data Mining (ICDM 2012). Piscataway, NJ: IEEE, 2012: 84-95 [7]Li C, Hay M, Miklau G, et al. A data- and workload-aware algorithm for range queries under differential privacy[J]. Proceedings of the Very Large Database Endowment, 2014, 7(5): 341-352 [8]Kellaris G, Papadopoulos S. Practical differential privacy via grouping and smoothing[J]. Proceedings of the Very Large Database Endowment, 2013, 6(5): 301-312 [9]Zhang X, Chen R, Xu J, et al. Towards accurate histogram publication under differential privacy[C]Proc of the 14th SIAM Int Conf on Data Mining (SDM 2014). Philadelphia, PA: SIAM, 2014: 587-595 [10]Li C, Hay M, Rastogi V, et al. Optimizing linear counting queries under differential privacy[C]Proc of the 41st Annual ACM Symp on Theory of Computing (PODS 2010). New York: ACM, 2010: 123-134 [11]Chen S, Zhou S. Recursive mechanism: Towards node differential privacy and unrestricted joins[C]Proc of the 2014 ACM SIGMOD Int Conf on Management of Data (SIGMOD 2014). New York: ACM, 2013: 653-664 [12]Zhang J, Cormode G, Procopiuc C M, et al. PrivBayes: Private data release via Bayesian networks[C]Proc of the 2014 ACM SIGMOD Int Conf on Management of Data (SIGMOD 2014). New York: ACM, 2014: 1423-1434 [13]Zhu T, Xiong P, Li G, et al. Correlated differential privacy: Hiding information in non-iid data set[J]. IEEE Trans on Information Forensics and Security, 2015, 10(2): 229-242 [14]Kusner M J, Jacob R G, Roman G, et al. Differentially drivate Bayesian optimization[C]Proc of the 32nd Int Conf on Machine Learning (ICML). Brookline, MA: Microtome, 2015: 918-927 [15]Su S, Xu S, Cheng X, et al. Differentially private frequent itemset mining via transaction splitting[J]. IEEE Trans on Knowledge and Data Engineering, 2015, 27(7): 1875-1891 [16]Xiao X, Xiong L, Yuan C. Differential privacy via wavelet transforms[J]. IEEE Trans on Knowledge and Data Engineering, 2011, 23(8): 1200-1214 [17]Hay M, Rastogi V, Miklau G, et al. Boosting the accuracy of differentially private histograms through consistency[C]Proc of the 36th Int Conf on Very Large Data Bases (VLDB 2010). New York: ACM, 2010: 1021-1032 [18]Rastogi V, Nath S. Differentially private aggregation of distributed time-series with transformation and encryption[C]Proc of the 2010 ACM SIGMOD Int Conf on Management of Data (SIGMOD 2010). New York: ACM, 2010: 735-746 [19]Yuan G, Zhang Z, Winslett M, et al. Low-rank mechanism: Optimizing batch queries under differential privacy[J]. Proceedings of the Very Large Database Endowment, 2012, 5(11): 1352-1363 [20]Samarati P. Protecting respondents’ identities in microdata release[J]. IEEE Trans on Knowledge and Data Engineering, 2001, 13(6): 1010-1027 [21]Machanavajjhala A, Kifer D, Gehrke J, et al. l-diversity: Privacy beyondk-anonymity[J]. ACM Trans on Knowledge Discovery from Data, 2007, 1(1): 1-36 [22]McSherry F, Talwar K. Mechanism design via differential privacy[C]Proc of the 48th Annual IEEE Symp on Foundations of Computer Science (FOCS 2007). Piscataway, NJ: IEEE, 2007: 94-103 [23]Rubinstein R, Kroese D. Simulation and the Monte Carlo Method[M]. New York: Wiley Heyden Ltd, 2008 [24]Gelman A, Rubin D. Inference from iterative simulation using multiplesequences[J]. Statistical Science 1992, 1(4): 451-511 [25]McSherry F. Privacy integrated queries: An extensible platform for privacy-preserving data qnalysis[C]Proc of the 2009 ACM SIGMOD Int Conf on Management of Data (SIGMOD 2009). New York: ACM, 2009: 19-30 Zhang Xiaojian, born in 1980. PhD, lecturer in the College of Computer and Information Engineering, Henan University of Economics and Law. His main research interests include differential privacy, data mining, and graph data management. Shao Chao, born in 1977. PhD, associate professor and master supervisor in the College of Computer and Information Engineering, Henan University of Economics and Law. His research interests include machine learning, data mining and visualization. Meng Xiaofeng, born in 1964. Professor and PhD supervisor at Renmin University of China. Executive director of China Computer Federation. His main research interests include cloud data management, Web data management, native XML databases, and flash-based databases, privacy-preserving, and etc. Accurate Histogram Release under Differential Privacy Zhang Xiaojian1, Shao Chao1, and Meng Xiaofeng2 1(CollegeofComputer&InformationEngineering,HenanUniversityofEconomicsandLaw,Zhengzhou450002)2(SchoolofInformation,RenminUniversityofChina,Beijing100872) AbstractGrouping-based differentially private histogram release has attracted considerable research attention in recent years. The trade-off between approximation error caused by the group’s mean and Laplace error due to Laplace noise constrains the accuracy of histogram release. Most existing methods based on grouping strategy cannot efficiently accommodate the both errors. This paper proposes an efficient differentially private method, called DiffHR (differentially private histogram release) to publish histograms. In order to boost the accuracy of the released histogram, DiffHR employs Metropolis-Hastings method in MCMC (Markov chain Monte Carlo) and the exponential mechanism to propose an efficient sorting method. This method generates a differentially private histogram by sampling and exchanging two buckets to approximate the correct order. To balance Laplace error and approximation error efficiently, a utility-driven adaptive clustering method is proposed in DiffHR to partition the sorted histogram. Furthermore, the time complexity of the clustering method is O(n). DiffHR is compared with existing methods such as GS, AHP on the real datasets. The experimental results show that DiffHR outperforms its competitors, and achieves the accurate results. Key wordsdifferential privacy; histogram release; grouping; Laplace error; approximation error 收稿日期:2015-04-17;修回日期:2015-10-19 基金项目:国家自然科学基金项目(61502146,61379050,U1404605,61202285);国家“八六三”高技术研究发展计划基金项目(2013AA013204);河南省科技厅基础与前沿技术研究项目(152300410091);河南省教育厅高等学校重点科研项目(16A520002);河南财经政法大学校重大研究课题(201426) 中图法分类号TP392 This work was supported by the National Natural Science Foundation of China (61502146,61379050,U1404605,61202285), the National High Technology Research and Development Program of China (863 Program) (2013AA013204), the Basic Research Program of Henan Science and Technology Department (152300410091), the Key Research Program of the Higher Education of Henan Educational Committee (16A520002), and the Key Research Program of Henan University of Economics and Law (201426).