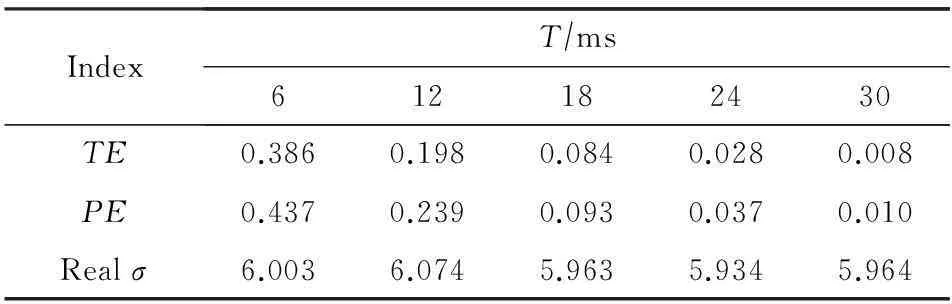
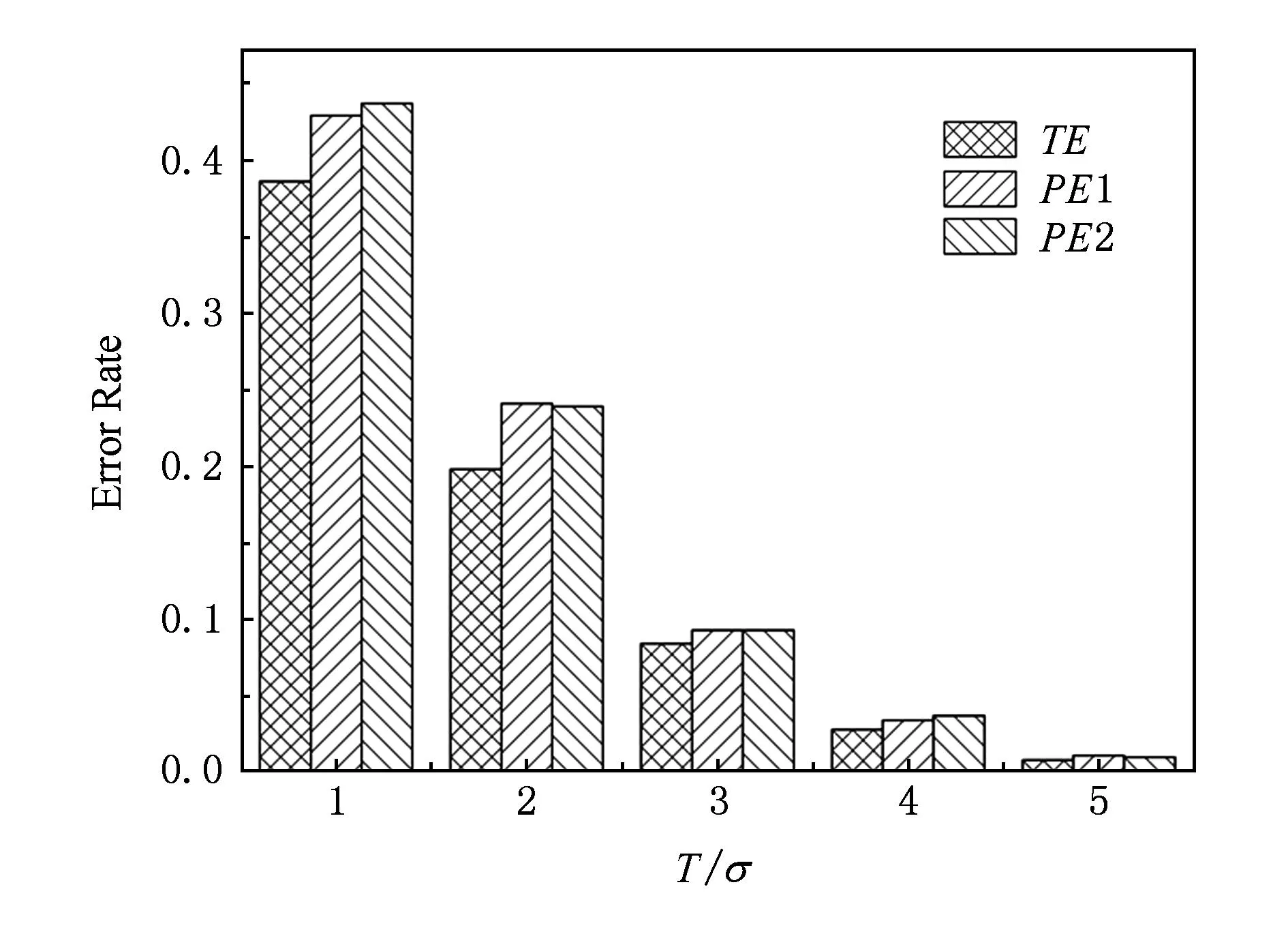
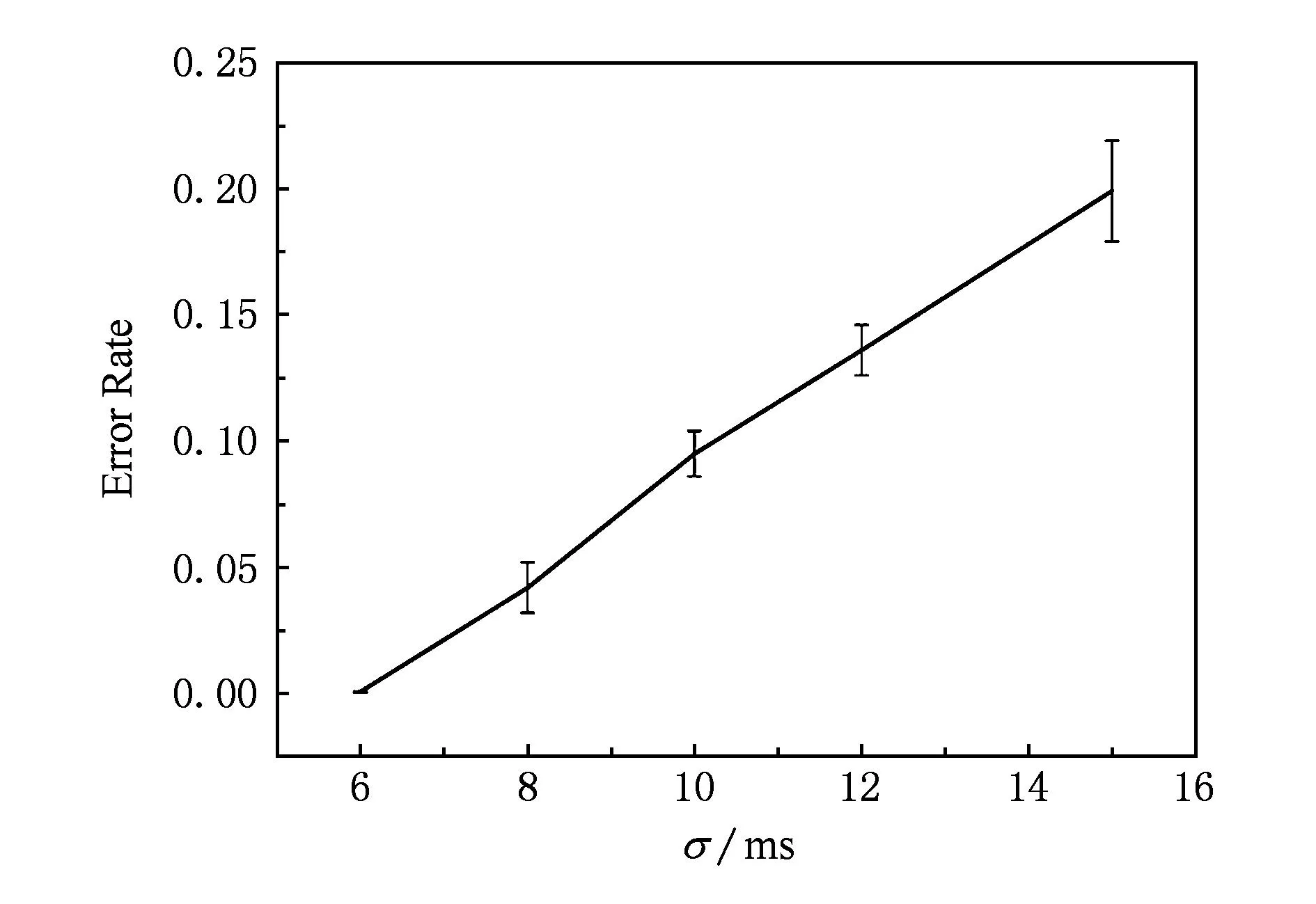
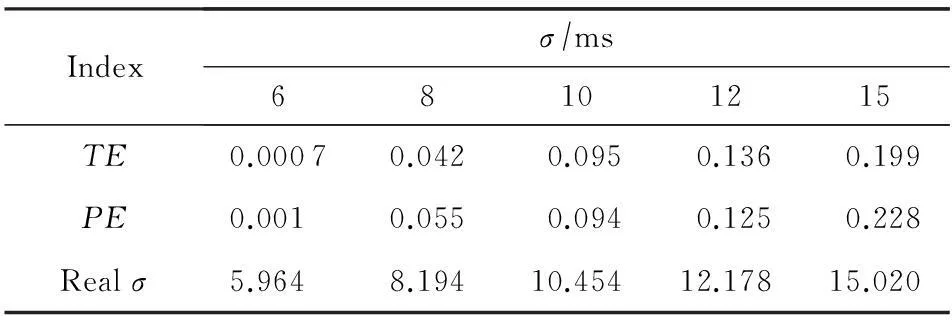
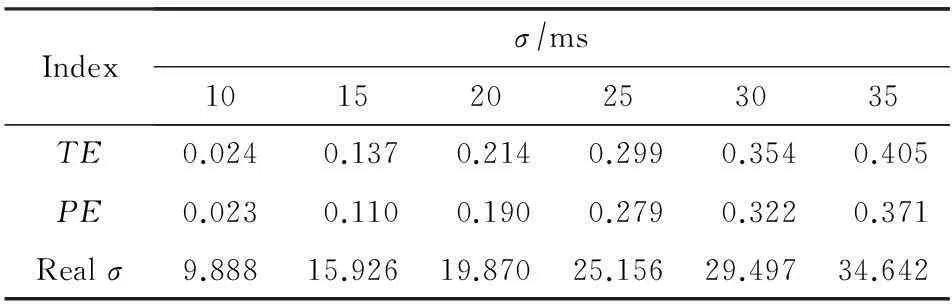
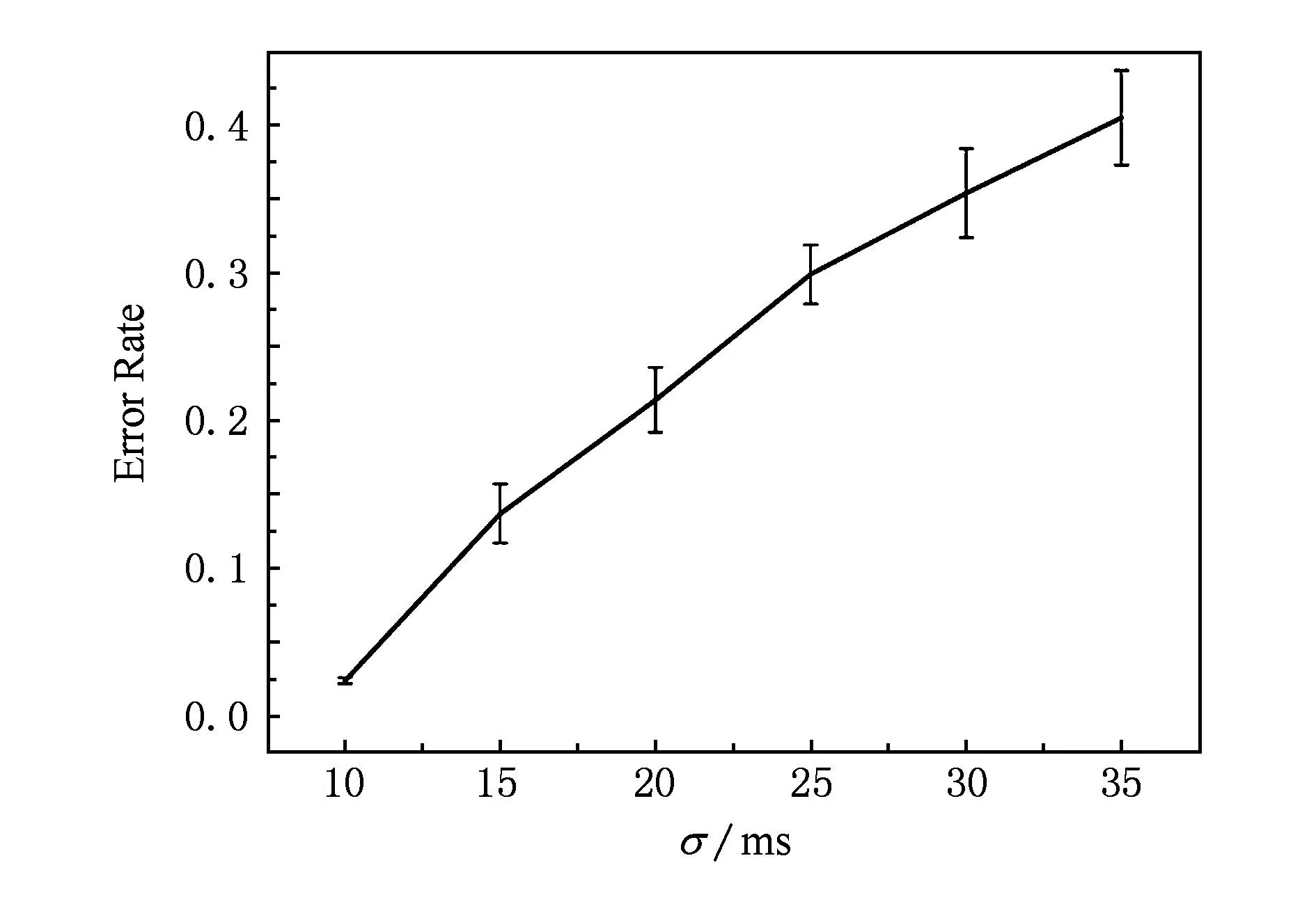
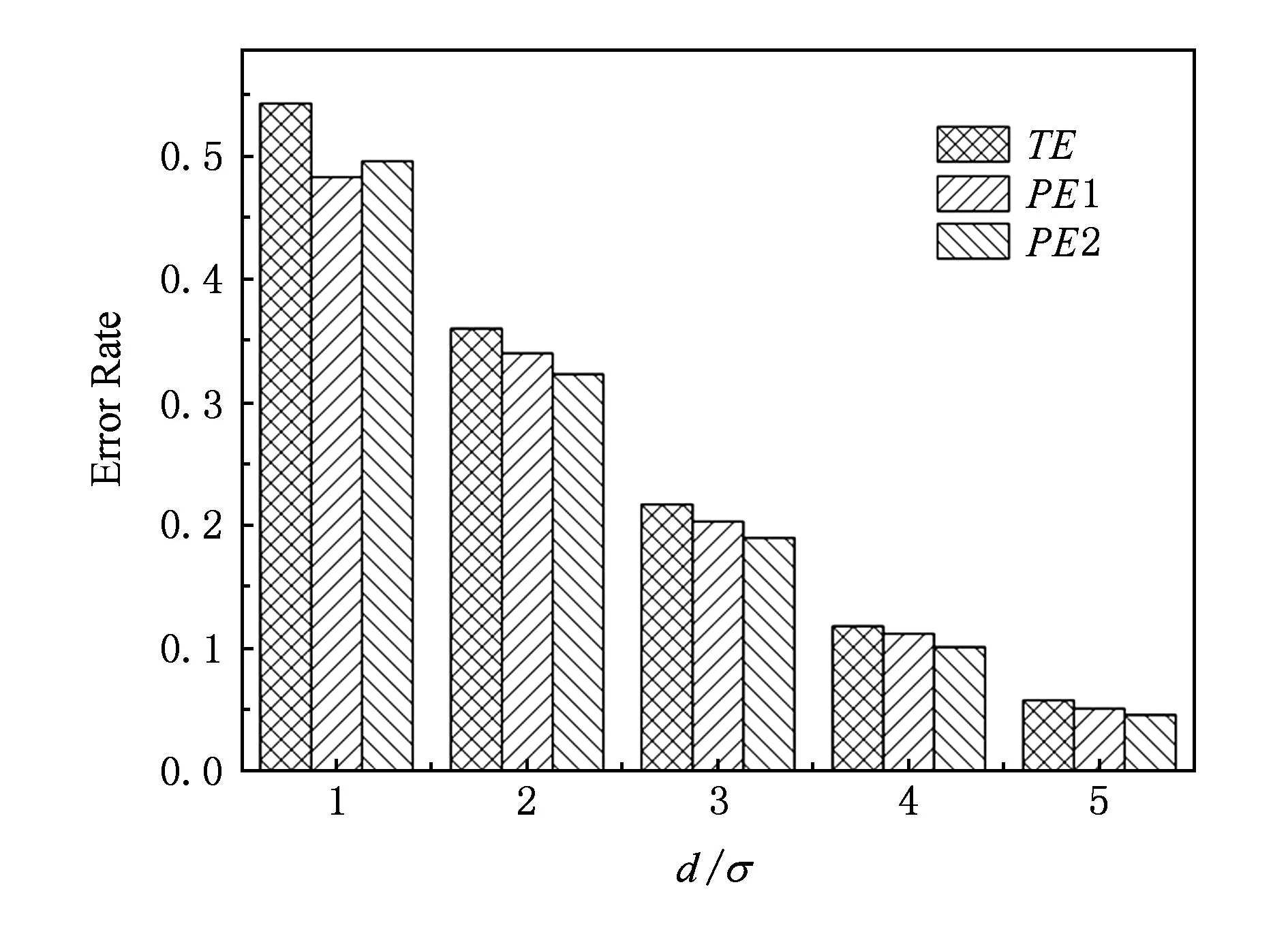
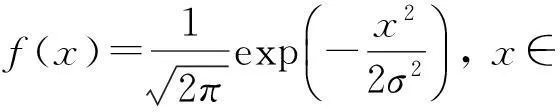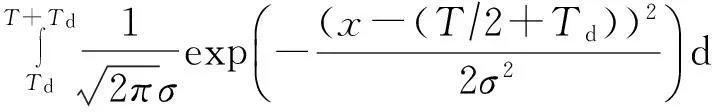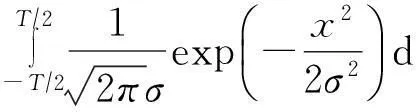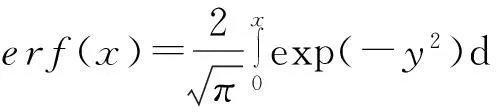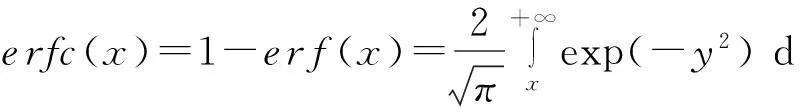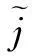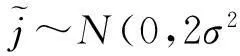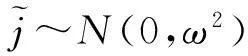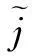IP时间隐通道的信息隐藏算法及其性能分析
2016-06-16王昌达刘志锋
王昌达 黄 磊 刘志锋
(江苏大学计算机科学与通信工程学院 江苏镇江 212013)(changda@ujs.edu.cn)
IP时间隐通道的信息隐藏算法及其性能分析
王昌达黄磊刘志锋
(江苏大学计算机科学与通信工程学院江苏镇江212013)(changda@ujs.edu.cn)
摘要隐通道(亦称隐蔽信道)是高等级可信系统评估的重要指标,而以时间作为信息传输载体的工作方式决定了IP时间隐通道在包交换网络中几乎不能被根除.目前,利用IP时间隐通道在网络中实施信息的隐蔽传输没有统一的数学模型,对其研究主要还是依靠实验方式.首先根据时间的物理定义,将IP时间隐通道按工作方式的差异分成不同类别;然后以随机过程为工具,建立了基于定长时隙与包间延迟2种IP时间隐通道的信息隐藏算法模型;最后在此基础上,推导出了其带宽和误码率与相关网络环境参数的函数关系,并对可获取的有效隐蔽通信带宽与网络噪声的影响进行了一般性的讨论.实验结果印证了提出的数学模型及其理论分析结果的正确性,由此IP时间隐通道的研究可以从主要依靠实验转化为形式化分析与实验验证相结合.
关键词IP时间隐通道;信息隐藏算法;带宽;误码率;鲁棒性
在包交换网络中,IP隐通道利用数据包中原本不是用于数据传送的资源来传送数据,所以这种通信方式一般不能被系统的固有安全机制所检测和控制.IP隐通道有2种类型:IP存储隐通道和IP时间隐通道.IP存储隐通道一般利用数据包报头暂未被通信协议使用的冗余位隐藏信息[1],初期吸引了大批研究者,对IP报头冗余位利用几乎达到极致[2].此后网络防火墙使用了流量正规化技术(traffic nor-malization),即将进出IP数据包的冗余位强制使用相同的格式改写,该方法有效地打击了IP存储隐通道[3].随后人们将目光转向更为隐蔽的IP时间隐通道,即接收方通过观察数据包到达的时间变化来解释、获取被传递的隐藏信息.世界上第1个公开报道的IP时间隐通道是美国普渡大学于2004年在校内的2个网络节点之间实现的,当时观测到的带宽为16.67 bps,误码率在2%~14%之间[4].因为带宽低、鲁棒性差,所以IP时间隐通道最初并未引起广泛的关注.但2年后,美国宾夕法尼亚大学的Shah等人[5]实现了一个能截取用户从键盘输入的密码并通过IP时间隐通道向外发送的软件,而2010年Zi等人[6]又实现了以网络中间节点作为发送方的被动式IP时间隐通道,且Zander等人[7]经过统计认为,即使IP时间隐通道每个数据包只携带1 b的信息,那么1个大型网站1年将隐蔽流失约26 GB的数据量.这些工作重新引燃了人们对IP时间隐通道的重视.
隐通道是实现网络匿名通信的有效方法[8],美国的TCSEC,ISO的CC和我国的GB17859—1999等标准中均有相关要求.因为时间作为发送方和接收方的共享资源是不可割断的,所以IP时间隐通道在网络系统中几乎不能被根除[9].目前已经认识到IP时间隐通道的应用可以分为2类:1)利用IP时间隐通道抵抗监听.若保密节点之间的通信不可避免地处于敌方的监控之下,那么两者之间的任何异动,如频繁交换信息或更换高强度密码都将引起敌方的警觉.而借助IP时间隐通道的方式,将秘密信息的发送隐藏于日常非机密的事物性信息流中,可以有效规避敌方的监控和警觉.2)利用IP时间隐通道制作数据流水印.在匿名通信系统中,将一段用IP时间隐通道表示的信息嵌入到数据包流中作为水印,用以监视敏感数据的真实走向或用以追查和取证匿名网络攻击.
目前IP时间隐通道没有统一的数学模型,因此其关键性能指标如带宽和误码率等,主要依靠实验测定,无法进行理论估算.而建立IP时间隐通道的数学模型必须首先解决时间信号的消息嵌入与提取算法问题.时间变量作为一种非常规信息载体信号缺乏系统的理论研究.本文的主要贡献在于:
1) 给出了时间信号调制与解调的基本方式;
2) 建立了IP时间隐通道的随机过程数学模型;
3) 对IP时间隐通道的性能进行了形式化分析,并给出了具有一般性的结论,实验结果印证了理论分析的正确性.
1相关工作
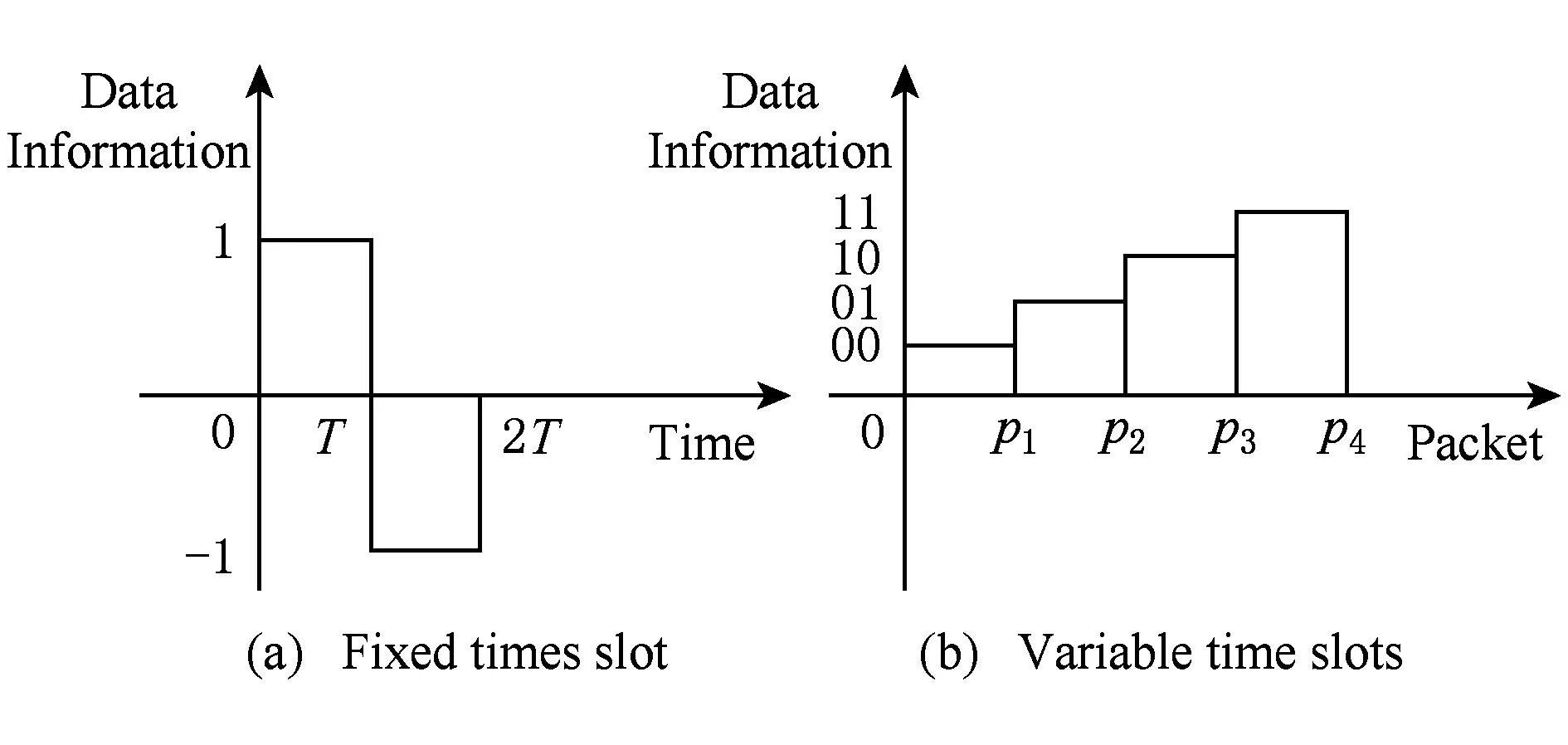
已知最早的IP时间隐通道实验在美国普渡大学完成[4].他们采用固定长度的时间窗口隐藏信息,即接收方以时间间隔Δt为单位将时间线划分成若干个相邻的窗口,从第1个窗口开始,若有发送方传来的数据包到达则接收二进制信息“1”,否则接收二进制信息“0”,然后逐次转向其后的窗口接收信息.这种方法存在着明显的技术缺陷,即要求发送方与接收方时钟同步.若被传送的二进制信息中0和1以等概率出现,则平均一个数据包可以承载2 b的信息.其后Berk等人[10]提出通过传输连续2个数据包之间的时间差值变化隐藏信息.这样连续传输的n+1个数据包共可承载n个时间差变量.若将这些参数作为一个n维向量对待且每个参数有m种不同的取值,则平均每个数据包可以携带的信息量是mn(n+1)(单位为b).又因为采用相对的时间差值,所以这种方法不需要收发双方的时钟同步.
时间隐通道的分析可以概括为检测、审计和消除3个部分[11].对其工作模式的刻画决定了隐通道的检测方法[12].现有的检测方法可以分为2类:形状参数检验和规律性检验.形状参数检验主要是分析数据的1阶统计参数,包括平均值、方差以及概率分布;而规律性检验则是分析数据间的相关性,采用2阶或高阶统计量,度量数据的概率分布规律性[13].目前采用的检测指标主要有3种:Cabuk等人的数据包间隔方差指标[9]、Berk 等人的数据包间隔概率分布相似度指标[10]和Gianvecchio等人的数据包间隔熵率指标[14].这些检测方法的指导思想是:IP时间隐通道使用数据包的达到时间变化隐藏信息,故其时间分布特性必然区别于正常的网络数据包.所以若IP时间隐通道中的数据包与网络中正常数据包的传输时间满足相同的分布函数,这些检测技术将失效[15],因此出现了IP时间隐通道的隐藏方法[15-16].
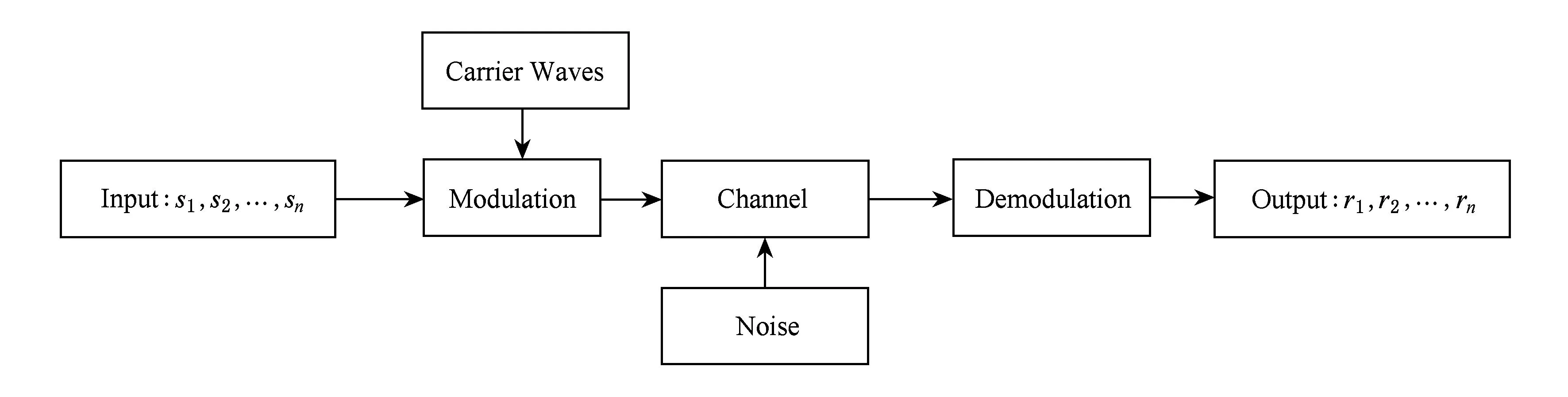
Fig. 1 The communication model of IP covert timing channels.图1 IP时间隐通道的通信模型
早期隐藏技术的不足之处在于需要计算待伪装分布函数的反函数,但分布函数是积分变上限函数或下限函数,所以这样的反函数可能没有解析解[17].网络中IP数据包传输时间的分布函数具有多样性[18],故应用这类抗检测方法具有较大的局限性.我们课题组提出的基于蒙特卡罗方法的IP时间隐通道隐藏方法(见文献[19])较好地解决了这一问题.
目前IP时间隐通道的消除方法主要有:流量控制法[20]、泵协议法[21]和混沌时间法[22]等,这些方法大多来源于多安全级可信系统中时间隐通道消除方法的改进.其本质均是通过增加信道中的噪声使接收方无法以较低的误码率还原出被传送的信息而致瘫.与传统的隐通道审计方式一致,IP时间隐通道也使用带宽作为审计指标[11].
相对于其他的网络安全问题,IP时间隐通道的研究起步较晚.目前多是以朴素的信息传递思想实现了IP时间隐通道的基本通信功能,并进一步在实验的基础上,借助前人在多安全级可信操作系统中关于时间隐通道的研究成果,提出了IP时间隐通道的检测和消除方法,见文献[9,15,23].但IP时间隐通道和多安全级操作系统中的时间隐通道存在着显著的差别:首先,IP时间隐通道通过数据包到达的时间变化传递信息,而多安全级操作系统中的时间隐通道则是通过对操作系统中的共享资源竞争所获得的服务时间差异传递信息[1];其次,在IP时间隐通道中,数据包一旦进入网络,其传输将完全不受发送方和接收方的控制,只取决于网络当前的拥塞状态,其传输过程是典型的随机事件,而在多安全级操作系统中,具有不同安全级的主体拥有不同的权限可以控制对共享资源的使用时间,因此其传输过程在发送方与接收方的合作下是可控且确定的.
IP时间隐通道没有统一的数学模型,无法预先求得其在给定网络环境下可证明的极限带宽和通信误码率,亦无法建立它们与网络环境参数之间的函数关系.因此不管是在Cabuk等人[4]还是在Sellke等人[15]的工作中,在这些已知最为成功的关于IP时间隐通道的实验中,其功能参数均是通过实验测出的近似值,而不是通过形式化推导求出的最优解.
2时间信号的调制解调
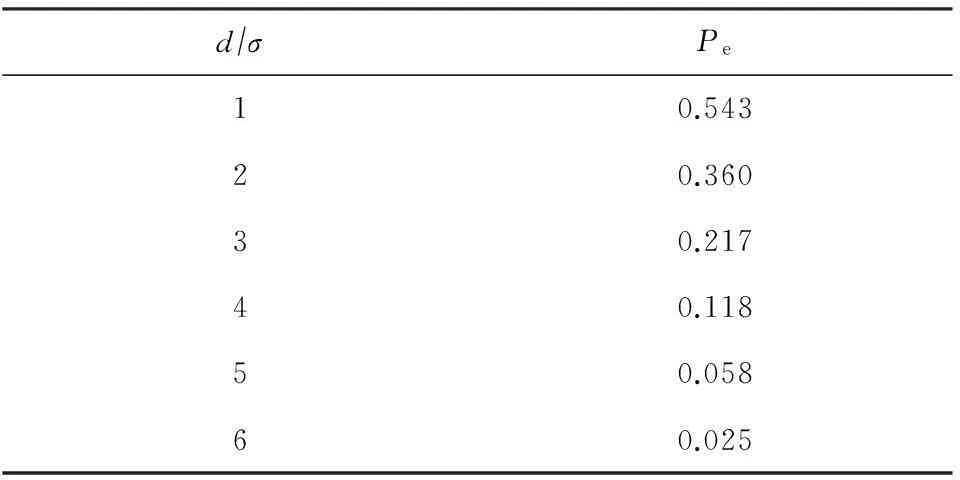
IP时间隐通道是包交换网络之上的一种非常规寄生式信道,它利用数据包携带的时间信号变化实施通信,但时间信号在网络传输中会受到多种随机噪声的干扰,被干扰的时间信号会发生畸变.
基于这样的认识,我们利用随机过程理论定义IP时间隐通道并建立对应的数学模型.首先,我们研究IP时间隐通道的工作原理.通过归纳分析,我们给出其工作原理如图1所示,其特征是:IP时间隐通道的输入信号{s1,s2,…,sn}是一组关于时间t的变量,通过调制器将{s1,s2,…,sn}转变为网络介质中的时间信号进行远距离传输;在信道的另一端通过解调器对时间信号解调,得到另外一组关于时间t的变量{r1,r2,…,rn}.因为网络中噪声的干扰,所以在传输的过程中,时间信号si会发生畸变,因此一般地,si≠ri,i=1,2,…,n.
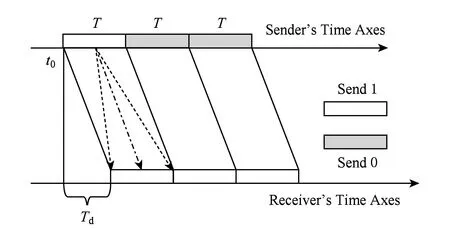
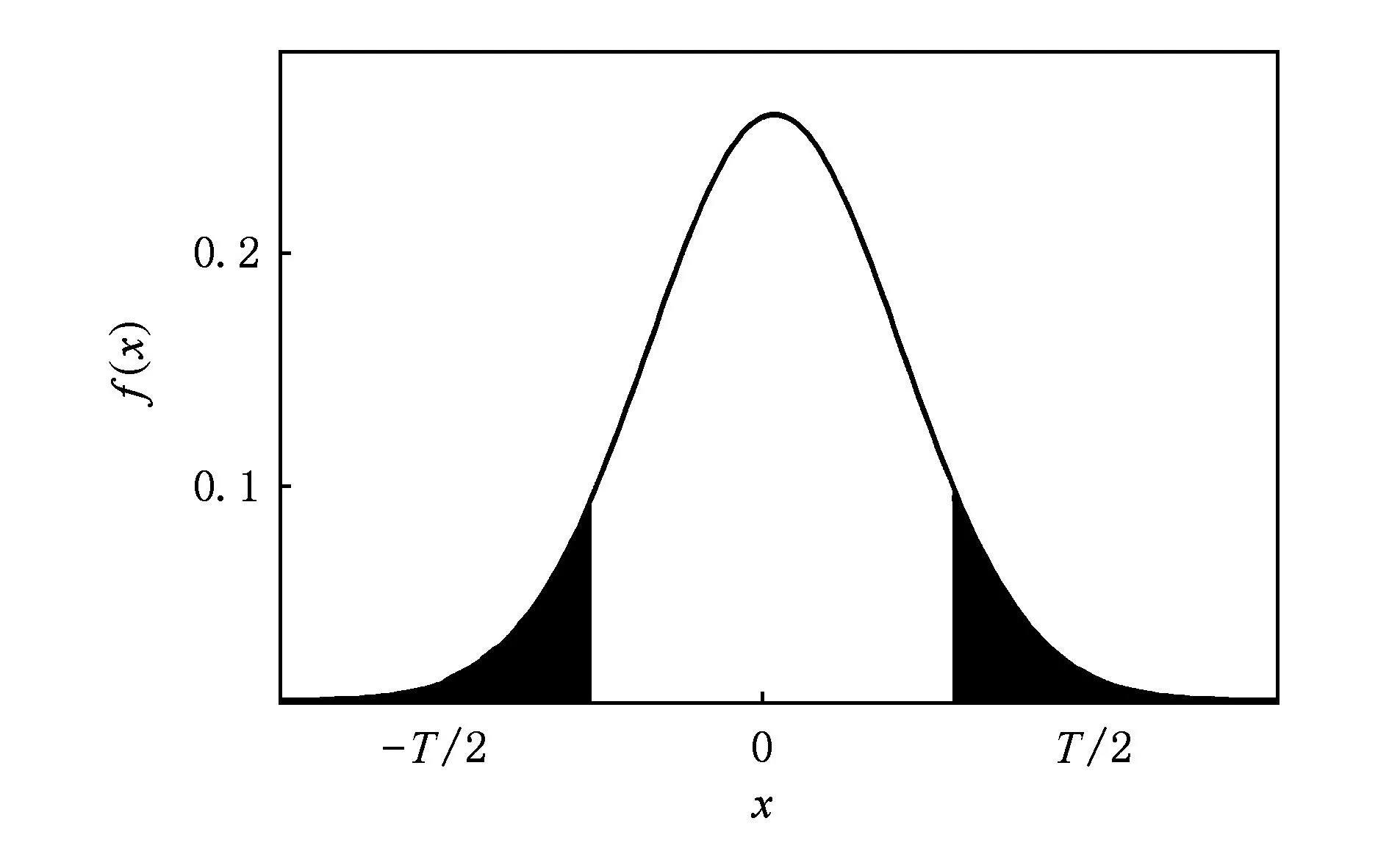
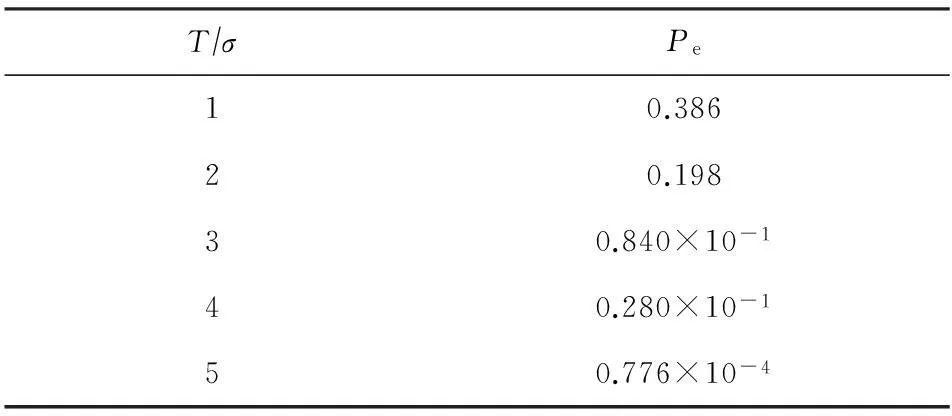
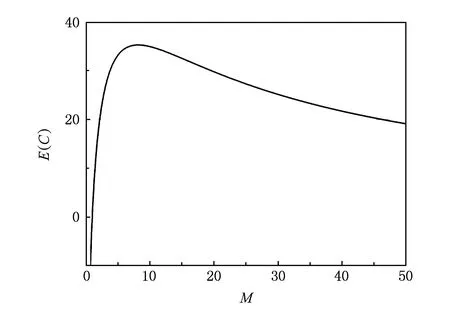
条件概率P(si|rj)的值刻画了IP时间隐通道对时间信号正确传输的性能.在没有噪声干扰的情况下P(si|rj)=1,即可根据接收信号完全确定发送信号,此时信道的误码率为0.但受网络中噪声的干扰,0 2.1IP时间隐通道的数学定义 我们借助时间信号的概念给出IP时间隐通道的数学定义. 定义1. IP时间隐通道.在包交换网络中,若通信双方使用 (1) 作为通信中消息的载体,那么这样的信道称为IP时间隐通道.其中{IP_Packet}表示IP数据包的集合,si(pi)表示pi携带的时间信号. 定义1可以从2个角度进行理解:1)s(p)是n种关于T的不同信号的线性组合,如图2所示.组合不同,传递的消息也不同;2)IP时间隐通道是通过数据包携带的时间信号变化通信的,但未对数据包本身的结构实施任何改动. Fig. 2 Communication by the amplitudes of timing signals.图2 利用时间信号的振幅通信 在常规通信技术中,广泛使用的信号是简谐波信号,在这种载波信号中,时间t被作为唯一的独立变量[23],且根据调制参数的不同,其通信方式对应的有调幅、调频和调相3种.而在定义1中,数据包pi是唯一的独立变量,时间t不再是独立的变量,而是变量pi的函数,所以t被用作调制消息的信号.若将si(pi)表示的信号利用T的数值大小进行区分,即将T解释成一种关于时间的波形信号的振幅,那么可将这种通信方式理解成调幅通信,如图2所示. 2.2IP时间隐通道的基本型 在调制时间信号之前,需要知道时间信号具有哪些可以被调制的特性. 物理学中关于时间的定义是:时间是一个衡量系统,它被用来度量事件发生的顺序、事件的持续长度以及事件之间的间隔,时间也被用来量化客体的改变率.基于这样的定义,我们提出IP时间隐通道中传输的时间信号至少有3种不同的调制方式. Ⅰ型.在固定的时间间隔Δt内,通过有或无数据包到达,传递可根据数据包个数差异识别的时间信号si(i=0,1); Ⅱ型.给定一组n个数据包,通过连续到达数据包的间隔时间Δti∈{Δt1,Δt2,…,Δtn-1},传递可根据Δti差异识别的时间信号si(i=1,2,…,n-1); Ⅲ型.给定一组n个数据包,其到达的顺序是pi∈{P},其中{P}是该组数据包标识的全排列,传递可根据数据包标识排列差异识别的时间信号si(i=1,2,…,n!). 这3种类型分别对应时间定义中的“量化客体的改变率”、“度量事件之间的间隔”和“度量事件发生的顺序”.其中Ⅰ型可以看作是调控客体在单位时间内的改变率;Ⅱ型可以看作是调控事件之间的间隔;Ⅲ型可以看作是控制事件发生的顺序. 这3种类型构成了IP时间隐通道的基础通信模式.因此无论一个具体的IP时间隐通道采用何种时间信号,其底层必是通过“量化客体的改变率”、“度量事件之间的间隔”或“度量事件发生的顺序”实现的. Fig. 3 Signal modulation of IP covert timing channels.图3 IP时间隐通道的信号调制 3算法模型及其性能分析 本节在时间信号调制解调方法的基础上,利用随机过程理论建立IP时间隐通道的算法模型,并对其性能进行分析. 3.1Ⅰ型IP时间隐通道 在Ⅰ型中,发送方若在一个定长为T的时间窗口内发送了一个数据包,那么接收方在对应的时间窗口内能否观测到该数据包就决定了Ⅰ型传输消息的正确性. 一般地,数据包在网络中的传输时间受到2种噪声的干扰:传输时延Td和时延抖动j.数据包的传输平均时延Td是数据包在网络上传输平均所必须消耗的时间,它与网络中设备的硬件性能和传输距离有关.当Td→∞时,可认为数据包丢失.而时延抖动j则是具体数据包在网络中传输所消耗的时间与平均时延的偏离值,即ji=Ti-Td.从概率的角度观察,集合J(ji∈J,i∈+)是一组随机变量,其密度函数为 (2) 即J作为一组随机变量满足均值E(ξ)=0,方差D(ξ)=σ2的正态分布. 理想地,对任意j∈J,j=0.此时若发送方起始时间点为t0,时间窗口的长度为T,则接收方应选择t0+Td为起始点,并以T为时间窗口长度观测数据包的到达.若发送的时间点是窗口的中点t0+T2,那么数据包的到达的时间为t0+Td+T2.因必有(t0+Td+T2)∈[t0+Td,t0+Td+T],所以发送的数据包一定落在对应的观察窗口之内,故无论发送0或1,都能被正确接收,如图4所示: Fig. 4 Noise interferences for IP covert timing channels.图4 IP时间隐通道的噪声干扰 一般地,因为时延抖动j≠0,所以发送方在t0+T2发送的数据包,并不能保证在t0+Td+T2时刻到达,其到达的时刻为预期到达时刻与该数据包的时延抖动值之和:Tarrival=(t0+Td+T2)+j,其中t0+Td+T2为在接收方时间作标轴上的数据包的期望到达时刻.显然只有Tarrival∈[t0+Td,t0+Td+T]成立,消息才能被正确接收,如图4所示. 因为j作为随机变量满足均值为0、方差为σ2的正态分布,可以证明在时间窗口的中点发送能够使得数据包落在观测窗口之内的概率最大,故第i个窗口的最优发送点为:t0+T2+(i-1)T,i∈+. 不失一般性,我们研究图4左侧第1个时间窗口.当采用最优时间发送点时,j∈J具有式(2)所表示的概率密度函数,所以数据包在[t0+Td,t0+Td+T]区间到达的概率为 P(t0+Td≤Tarrival≤t0+Td+T)= (3) 式(3)采用坐标平移化简后,可得结果: (4) 式(4)表示由式(2)表示的正态分布函数曲线与直线x=-T2和x=T2所围成的区域的面积,如图5所示,其几何意义是P(1|1),即发送1时被正确接收的概率.此时其误码率是: (5) 式(5)的几何意义是P(0|1),即发送1时接收0的概率,其值为图5中2块阴影面积之和. Fig. 5 Density function curve of packets transmission delay.图5 时延抖动的密度函数图像 根据图4,可以直观看出Ⅰ型在发送1或者0时,两者在接收方解码的误码率并不相同.这是因为发送0时,在发送方的时间窗口T内,并无数据包传送,因此在对应的接收方时间窗口内若能接收到某个数据包而产生误码,该数据包只可能来自发送方当前发送窗口的左侧(因为数据包不会在尚未发送之前就到达).这表明P(1|0)的计算依赖于其左侧的若干个时间窗口,是典型的Markov链. 为简化问题规模,我们只计算一步Markov链的转移,即认为P(1|0)只与其左侧紧邻的时间窗口有关.这个假设的合理性在于:1)正态分布的随机变量在远离其均值的位置,事件的概率迅速下降,因此当前时间窗口左侧更远的窗口对当前窗口接收数据造成干扰的概率很小,在[3σ,-3σ]区间以外,误差小于3‰;2)在网络中,一个数据包若在设定的时间内没有到达,依据网络协议可能会要求重传或者被直接丢弃,因此相邻左侧的n个时间窗口对当前时间窗口的干扰,对n会有长度限制.因此当T≫σ时,使用多步Markov链计算意义不大. 因此,若Ⅰ型传送的二进制消息中0和1以等概率出现,那么有: (6) 式(6)中的定积分表示图5右侧阴影部分的面积,即当前时间窗口中的数据包进入下一个时间窗口的概率.其前面给出系数12,是因为若当前时间窗口的左侧发送的是0,即无数据包,那么对于当前时间窗口接收0也不会形成干扰,只有当前时间窗口的左侧发送的是1才可能形成误码,又因为假设0和1在所有被传输的二进制消息中以等概率出现,所以Ⅰ型的误码率是: Pe=P(1)P(0|1)+P(0)P(1|0)= (7) 因为erfc(x)是严格单调递减函数,所以式(7)表明时间窗口长度T越大,时延抖动的均方差σ越小,误码率越低,如表1所示: Table 1 Error Rates with Tσ 表1 误码率与Tσ的关系表 Table 1 Error Rates with Tσ T∕σPe10.38620.19830.840×10-140.280×10-150.776×10-4 尽管Ⅰ型需要收发双方时钟同步,难以精准实现,但这并不意味Ⅰ型没有实用价值.我们课题组在Ⅰ型实验中,将时钟同步误差计入数据包传输的时延抖动噪声中.表1中的数据表明,这样的处理方式,当观测窗口的长度T>5σ时,误差可控制在110 000以内.亦即较大的时钟同步误差需要引入较大的观测窗口长度. 因为Ⅰ型在每个定长时间窗口T内传送1 b的信息,因此其带宽C=1T. 3.2Ⅱ型IP时间隐通道 若在n+1个连续数据包所形成的n个间隔时间(T1,T2,…,Tn)中调制承载L(单位为b)的信息,且有:Ti=Δ+id,i∈[0,1,…,M-1].其中Δ>0,M∈+,即每个Ti共有M种不同的取值,其中Δ代表系统中可区分的数据包间最短间隔;d是间隔步长.那么n,M,L作为整数满足如下的函数关系:Mn=2L,即:L=nlbM. 为获取最大通信带宽,最好情况下,n个间隔都使用最小值Δ;最坏情况则是n个间隔都取最大值Δ+(M-1)d,因此Ⅱ型的带宽C满足不等式: (8) 不失一般性,设Ti的M种取值在通信中以等概率出现,那么Ti的期望值是:E(Ti)=Δ+(M-1)d2,所以Ⅱ型带宽的均值为 (9) 式(8)(9)分别给出了Ⅱ型带宽的上界、下界和均值.Ⅱ型的平均带宽E(C)与M之间的函数关系如图6所示.在n,Δ,d给定的情况下,为获得较高带宽,M存在最优解,即方程∂E(C)∂M=0的最接近整数解.在图6中,当n=4,Δ=50,d=10时(Δ,d的单位为ms),其最优整数解是8. Fig. 6 The curve of E(C) function.图6 E(C)的函数图像 下面我们研究Ⅱ型的误码率.若Ti=Δ+id,i∈[0,1,…,M-1],即每个Ti共有M种不同的取值,且任意2种不同间隔的差值为d的整数倍.与Ⅰ型讨论相同,噪声nc是数据包在网络传输中的抖动时间j∈J.因此当发送间隔为Ti时,接收到的间隔是Ti+ji.根据随机过程理论,可证明d2是接收信号判定的最优阈值[27],即对于接收的时间信号Tr,若|Tr-Ti|≤d2,i∈[1,2,…,n],则判定:Tr=Ti.所以当ji超过判决阈值d2时,在接收方对信号产生误判.但有2种情况例外:1)当Ti=Δ时,因为没有更小的间隔,所以即使对应的时延抖动ji<-d2也不会发生误判(总是被解释为最小间隔);2)当Ti=Δ+(M-1)d时,因为没有更大的间隔,所以即使时延抖动ji>d2也不会发生误判(总是被解释为最大间隔).当Ti的M种取值在通信中以等概率出现时,其平均误码率为 (10) Tr=tk+1+Td+jk+1-(tk+Td+jk)= (tk+1-tk)+(jk+1-jk)= (11) (12) 因为erfc(x)是严格单调递减函数,式(12)表明,当M给定时,步长d越大,时延抖动的均方差σ越小,误码率越低,如表2所示: Table 2 Error Rates with dσ(M=4) 表2 误码率与dσ的关系 (M=4) Table 2 Error Rates with dσ(M=4) d∕σPe10.54320.36030.21740.11850.05860.025 (13) 式(13)表明,当时延抖动均方差σ较大时,为保证Δ能可靠地传输,其取值也须相应增大. 3.3实验 在相关基金项目的支持下,课题组历时4年多开发了IP时间隐通道的综合实验平台.该系统支持宿主信道、时间信号编码方式等参数的可视化设置,此外系统还将信道中传输的消息采用分段封装,每段消息由数量固定的K(K≥2)个数据包分组负载.采用封装较好地解决了在传输过程中由于数据包合并或者拆分导致的时间信号误码散播问题. Fig. 7 Information transmission model of IP covert timing channels.图7 IP时间隐通道的信息传输模型 系统的工作模型如图7所示.对于Ⅰ型IP时间隐通道,在实验平台中我们仍然采用调制包间间隔的方式进行通信,即在相同的时间轴上,通过控制包间间隔调制在固定长度的时间窗口内数据包的发送和到达进行编码和解码.对于Ⅱ型IP时间隐通道,由于解码完全依赖于观测到的包间间隔,所以必须对接收的包间间隔进行校正,否则直接获取的间隔数值很可能没有对应的编码信息.因此我们给出一个判决阈值v,规定当接收间隔与某个发送间隔的差的绝对值小于阈值v,那么认定接收间隔即是此发送间隔.若编码表中采用了n种间隔时间T1,T2,…,Tn,且观测到的包间间隔时间为x,那么校正函数adjust(x)为 (14) 与Ⅰ型中的讨论相同,可以证明若这n种间隔之间的步长为d,其最佳判决阈值v=d2. 在使用IP时间隐通道正式通信前,收发双方需共享通信参数表,这包括:编码方案、观测窗口长度T、包间最小间隔Δ和间隔步长d.为避免每次通信前均需进行参数的协商,我们设计了一种双盲的策略,其基本思想是:根据网络中IP数据包传输的状态动态地选择通信参数. 根据本文中的式(7)(12)(13),在误码率给定的情况下,T,Δ,d与数据包传输时延抖动的均方差σ成正比关系.因此在发送方和接收方不再简单地预存编码方案和T,Δ,d的数值,而是仅预存编码方案和一个实数三元组(x,y,z),并定义: (15) 即根据σ的取值范围动态地选取T,Δ和d.当编码方案和可接受的误码率给定时,(x,y,z)的值可由式(7)(12)(13)确定.其中σ的测量方法是:发送方和接收方各自独立地向对方或是网络中的某些节点发送若干个嗅探数据包,并根据嗅探数据包的发送和到达时间测量σ. 在理想的情况下,若发送方的(T,d,Δ)=(xti,yti,zti),接收方的(T,d,Δ)=(xtj,ytj,ztj),则有|i-j|=0.即发送方和接收方采用的通信参数完全一致.若|i-j|≠0,不妨设|i-j|=K(K≥1),即发送方和接收方独立测定的σ落在了邻近不同的分段区域中,此时解码出的明文必不正确,或无法还原出正确的明文文件格式,或解码出的明文不具有可读性.我们设计的实验平台是异步解码的,即先将提取出的包间间隔信息保存后再进行解码.因此当|i-j|=K(K≥1)时,接收方可以通过遍历j的邻域找出正确的参数,例如当K=1时,仅需遍历j-1和j+1共2种状态即可找出正确的解码方案. 为了在网络中能够人为控制数据包传输的抖动时间,系统在发送端向编码后的数据包传送间隔中逐次注入噪声{t1,t2,…},其中{t1,t2,…}是使用Matlab生成的均值为0、方差为σ的一组正态分布随机变量,以此模拟网络中数据包传输的抖动时间.需要指出的是:1)若更换不同的分布函数,这种方法可以生成满足不同分布的数据包传输抖动时间;2)因为Matlab并不能确保这样生成的有限个随机变量其方差恰好是σ,且在实验中IP数据包在局域网中传输也会引入较小的传输抖动时间,所以在以下的实验中σ的理论值和实际观测值之间存在误差. 3.4实验结果 在Ⅰ型中,取σ=4 ms来产生随机时延,通信采用的观测窗口长度分别取4 ms,8 ms,12 ms,16 ms和20 ms.对每一个不同长度的观测窗口,传输5 000个数据包,然后取测量的平均值,如表3所示,其中TE表示理论误码率,PE表示实测误码率,Realσ表示实测的σ值.在表4中,σ=6 ms,通信采用的观测窗口长度分别取6 ms,12 ms,18 ms,24 ms和30 ms,同样对每一个观测窗口传输5 000个数据包,然后取测量的平均值.根据式(7),Ⅰ型的误码率由Tσ决定,所在表3和表4中TE的值相同. Table 3Error Rates of Type Ⅰ, Where Observation Windows Have Various Lengths (σ=4 ms) 表3 基于变长观测窗口的Ⅰ型误码率(σ=4 ms) Table 4Error Rates of Type Ⅰ, Where Observation Windows Have Various Lengths (σ=6 ms) 表4 基于变长观测窗口的Ⅰ型误码率(σ=6 ms) Fig. 8 Error rates of type, where observation windows have various lengths.图8 基于变长观测窗口Ⅰ型的误码率 在图8中,纵坐标表示误码率,横坐标表示Tσ的值,TE标注的是理论估算的误码率,PE1标注的是表3中的实测误码率,PE2标注的是表4中的实测误码率.在图9中,纵坐标表示误码率,横坐标表示σ的取值,曲线TE标注的是表5中理论估算的误码率,在各观测点使用误差棒标注误差范围.由此可见,Ⅰ型的各项理论估算值与实验观测值吻合度高. Fig. 9 Error rates of type Ⅰ, where observation windows have fixed length.图9 基于定长观测窗口Ⅰ型的误码率 同样对Ⅰ型,将观测窗口长度固定为30 ms,σ分别取6 ms,8 ms,10 ms,12 ms,15 ms.在每个不同的σ取值下传输5 000个数据包,取测量的平均值,如表5所示: Table 5Error Rates of Type Ⅰ, Where Observation Windows Have Fixed Length (T=30 ms) 表5 基于定长观测窗口的Ⅰ型误码率(T=30 ms) 在Ⅱ型中,分别取σ=10 ms和σ=20 ms来产生随机时延,Δ与d的具体取值分别如表6和表7所示.根据式(11),Ⅱ型误码率由dσ决定,所以表6和表7中理论误码率的取值相同.表6和表7中每项实测值均为传输5 000个数据包的测量均值. Table 6 Error Rates of TypeⅡ (σ=10 ms) Table 7 Error Rates of Type Ⅱ (σ=20 ms) 在表8中,取Δ=30 ms,d=60 ms,M=4,σ分别取10,15,20,25,30和35,表8中每一项实测值为传送5 000个数据包的测量平均值. Table 8Error Rates of Type Ⅱ (Δ=30 ms,d=60 ms,M=4) 表8 Ⅱ型误码率(Δ=30 ms,d=60 ms,M=4) Fig. 11 Error rates of type Ⅱ (Δ=30 ms,d=60 ms,M=4).图11 Ⅱ型的误码率(Δ=30 ms,d=60 ms,M=4) 在图10中,纵坐标表示误码率,横坐标表示dσ的值,TE标注的轨迹是理论估算的误码率,PE1标注是表6中的实测误码率,PE2标注是表7中的实测误码率.在图11中,纵坐标表示误码率,横坐标表示σ的取值,使用曲线TE标注的轨迹是表8中理论估算的误码率,在各观测点使用误差棒标注误差范围.由此可见,Ⅱ型的各项理论估算值与实验观测值吻合度高. Fig. 10 Error rates of type Ⅱ,PE1(σ≈10),PE2 (σ≈20).图10 Ⅱ型的误码率,PE1(σ≈10),PE2(σ≈20) 4关于带宽的一般性讨论 下面讨论IP时间隐通道的带宽与其误码率之间的关系. 性质1. 在维持平均误码率Pe不变的情况下,IP时间隐通道的带宽C与数据包传输时延抖动的无偏标准差σ成反比. 证明. 对Ⅰ型IP时间隐通道,其平均误码率Pe由式(7)表达,若σ1>σ2,而Pe维持不变,那么必有T1σ1=T2σ2,故T1>T2,又因为其平均带宽C=1T,所以C1 对Ⅱ型IP时间隐通道,其平均误码率Pe由式(12)表达,若σ1>σ2,而Pe维持不变,那么则必有d1σ1=d2σ2,故d1>d2,又因为其平均带宽可由式(9)表示,所以E(C1) 证毕. 性质2. 若数据包传输时延抖动的无偏标准差σ→0,那么IP时间隐通道的带宽C→+∞. 证明. 对于Ⅰ型IP时间隐通道,其平均误码率Pe由式(7)表达,当σ→0,若维持Pe不变,即维持Tσ的比值不变,则必有T→0,而Ⅰ型的平均带宽C=1T,故有:C→+∞. 对于Ⅱ型IP时间隐通道,其平均误码率Pe由式(12)表达,当σ→0,若维持Pe不变,即维持dσ的比值不变,则必有d→0,且根据式(12)可知亦有Δ→0,故根据式(9)可知其平均带宽C→+∞. 证毕. 性质3. 若数据包传输时延抖动的无偏标准差σ→+∞,那么IP时间隐通道的带宽C→0. 性质3的证明与性质2类似,限于篇幅,在此省略. 性质1给出了在保证误码率相对稳定的状态下,时延抖动的均方差与带宽之间的关系.而性质2和性质3则分别给出了σ→ 0和σ→+∞时带宽的极限值.这些性质告诉我们,当系统中噪声较高时,可以通过牺牲带宽换得通信的可靠性.在Ⅰ型中,需要增大式(7)中T的值;在 Ⅱ 型中,则需要增大式(12)中d的值.在本文4.3节中,我们给出根据σ的取值范围动态地选取T,Δ,d的通信参数协商方案,即是在应用中自动化地寻求带宽和误码率之间可接受平衡的一种解决方案. 因此我们需要知道,网络中T和d的值是否能无限增大?一般地,若采用连续的数据包进行时间间隔的调制则不能.以TCPIP协议为例,当一个数据包的传输时间大于某个值时,接收方会要求该数据包重传,这将破坏接收方对T的接收.我们给出如下的改进方法:在网络数据包流中,以整数L≥1为步长选择数据包作为时间信号的载体.若连续2个数据包之间可嵌入的最大和最小间隔分别为ΔTmax和ΔTmin,那么基于L步长,可嵌入的时间范围为[L×ΔTmin,L×ΔTmax].这样既能按要求增大T或d的值,而又能够不对网络的性能造成显著影响. 当L相对较大时,即使不采用伪装算法,如文献[15-16,19],IP时间隐通道仍然具有一定的抗检测性.这种现象可以直观地理解为:每L个数据包中只有一个属于IP时间隐通道,而检测方因为不能准确地知道这个数据包的位置,只能使用全部数据包作为检测样本,这样一个数据包所携带的时间信息将被样本中其他L-1个数据包分摊,因此而降低了检出的概率.所以即便在σ较小不需要较大T或d的情况下,通过主动降低带宽可以换得IP时间隐通道抗检测性能的提高. 5结束语 本文系统地讨论了IP时间隐通道的分类,给出了形式化的IP时间隐通道定义及其时间信息隐藏的算法模型,求解了IP时间隐通道的带宽、误码率与网络噪声的函数关系.设计了一个多用途的IP时间隐通道综合实验平台,实验数据有效印证了理论分析结果的正确性.这些工作使得在分析IP时间隐通道时,能够依据网络中可测量的噪声参数直接计算其带宽和误码率.这为IP时间隐通道的研究从实验观测转向理论分析与实验验证相结合准备了一套较为完善的框架. 参考文献 [1]Trabelsi Z, El-Sayed H, Frikha L, et al. A novel covert channel based on the IP header record route option[J]. International Journal of Advanced Media and Communication, 2007, 1(4): 328-350 [2]Zander S, Armitage G, Branch P. An empirical evaluation of IP time to live covert channels[C]Proc of the 15th IEEE ICON. Piscataway, NJ: IEEE, 2007: 42-47 [3]Yao Lihong, Zi Xiaocao, Li Pan, et al. A study of onoff timing channel based on packet delay distribution[J]. Computers & Security, 2009, 28(8): 785-794 [4]Cabuk S, Brodley C, Shields C. IP covert timing channels de-sign and detection[C]Proc of the 11th Conf on Computer and Communications Security. New York: ACM, 2004: 178-187 [5]Shah G, Molina A, Blaze M. Keyboards and covert channels[C]Proc of the 15th USENIX Security Symp. Berkeley, CA: USENIX Association, 2006: 59-75 [6]Zi Xiaocao, Yao Lihong, Li Pan, et al. Implementing a passive network covert timing channel[J]. Computers & Security, 2010, 29(6): 686-696 [7]Zander S, Armitage G, Branch P. A survey of covert channels and countermeasures in computer network protocols[J]. IEEE Communications Surveys and Tutorials, 2007, 9(3): 44-57 [8]Zhou Yanwei, Yang Qiliang, Yang Bo, et al. A Tor anonymous communication system with security enhancements[J]. Journal of Computer Research and Development, 2014, 51(7): 1538-1546 (in Chinese)(周彦伟, 杨启良, 杨波, 等. 一种安全性增强的Tor匿名通信系统[J]. 计算机研究与发展, 2014, 51(7): 1538-1546) [9]Cabuk S, Brodley C, Shields C. IP covert channel detection[J].ACM Trans on Information and System Security, 2009, 12(4): 22-49 [10]Berk V, Giani A, Cybenko G, et al. Detection of covert chan- nel encoding in network packet delays, 2005536[R]. Hanover, NH: Department of Computer Science, Dartmouth College, 2005 [11]Wang Changda, Ju Shiguang, Zhou Conghua, et al. A measurement of covert channels threat[J]. Journal of Computers, 2009, 32(4): 751-762 (in Chinese)(王昌达, 鞠时光, 周从华, 等. 一种隐通道威胁审计的度量方法[J]. 计算机学报, 2009, 32(4): 751-762) [12]Wang Changda, Ju Shiguang.The dilemma of covert channels searching[G]LNCS 3935: Proc of the 8th Annual Int Conf on Information Security and Cryptology. Berlin: Springer, 2006: 169-174 [13]Wang Yongji, Wu Jingzheng, Zeng Haotao, et al. Covert channel research[J]. Journal of Software, 2010, 21(9): 2262-2288 (in Chinese)(王永吉, 吴敬征, 曾海涛, 等. 隐蔽信道研究[J]. 软件学报, 2010, 21(9): 2262-2288) [14]Gianvecchio S, Wang H. Detecting covert timing channels: An entropy-based approach[C]Proc of the 14th ACM Conf on Computer and Communications Security. New York: ACM, 2007: 307-316 [15]Sellke S, Wang C, Bagchi S, et al. TCPIP timing channels: Theory to implementation[C]Proc of the 28th IEEE INFOCOM. Piscataway, NJ: IEEE, 2009: 2204-2212 [16]Sellke S, Wang C, Bagchi S, et al. Camouflaging timing channels in Web traffic, 47907-2035[R]. West Lafayette, IN: Purdue University, 2009 [17]Ross S. Introduction to Probability Models[M]. New York: Elsevier Press, 2007 [18]Zhang Bin, Yang Jiahai, Wu Jianping. Survey and analysis on the Internet traffic model[J]. Journal of Software, 2011, 22(1): 115-131 (in Chinese)(张宾, 杨家海, 吴建平. Internet流量模型分析与评述[J]. 软件学报, 2011, 22(1): 115-131) [19]Wang Changda, Bo Zhaojun, Guan Xingxing, et al. Anti-detection technology of IP covert timing channels[J]. Application Research of Computers, 2012, 29(7): 2657-2664 (in Chinese)(王昌达, 薄兆军, 管星星, 等. IP时间隐通道抗检测技术的研究[J].计算机应用研究, 2012, 29(7): 2657-2664) [20]Wang Yi, Chen Ping, Ge Yi, et al. Traffic controller: A practi-cal approach to block network covert timing channel[C]Proc of IEEE ARES’09. Piscataway, NJ: IEEE, 2009: 349-354 [21]Kang M, Moskowitz I. A pump for rapid, reliable, secure communication[C]Proc of the 1st ACM Conf on Computer and Communications Security. New York: ACM, 1993: 119-129 [22]Hu W. Reducing timing channels with fuzzy time[C]Proc of the Computer Society Symp on Research in Security and Privacy. Piscataway, NJ: IEEE, 1991: 8-20 [23]Stillman R. Detecting IP covert timing channels by correlating packet timing with memory content[C]Proc of the IEEE SoutheastCon. Piscataway, NJ: IEEE, 2008: 204-209 [24]Houmansadr A, Borisov N. SWIRL: A scalable watermark to detect correlated network flows[C]Proc of the 18th Annual Network & Distributed System Security Conf. San Diego, CA: NDSS, 2011: 1-15 [25]Houmansadr A, Kiyavash N, Borisov N. RAINBOW: A robust and invisible non-blind watermark for network flows[C]Proc of the 16th Annual Network & Distributed System Security Conf. San Diego, CA: NDSS, 2009: 1-15 [26]Luo X, Zhou P, Zhang J, et al. Exposing invisible timing-based traffic watermarks with BACKLIT[C]Proc of the 27th Annual Computer Security Applications Conf. New York: ACM, 2011: 197-206 [27]Proakis J, Salehi M. Fundamentals of Communication Systems[M]. Upper Saddle River, NJ: Pearson Education Press, 2007 Wang Changda, born in 1971. PhD, professor and PhD supervisor. Member of China Computer Federation. His main research interests include network communication and security, WSNs, etc. Huang Lei, born in 1991. Master candidate. His research interest include network security (1132985083@qq.com). Liu Zhifeng, born in 1981. PhD, associate professor. His research interests include network security and model checking, etc (liuzf@ujs.edu.cn). Information Hiding Algorithm of IP Covert Timing Channels and Its Performance Analysis Wang Changda, Huang Lei, and Liu Zhifeng (SchoolofComputerScienceandCommunicationEngineering,JiangsuUniversity,Zhenjiang,Jiangsu212013) AbstractCovert channel analysis is one of the mandatory requirements of high-level trust evaluations. That IP covert timing channels utilize “time” as media to carry messages makes the eradication of IP covert timing channels on packets-switched networks, which is almost impossible. Hitherto, lack of a general mathematical model makes IP covert timing channels to be a tough job by which implement anonymous communication or information hiding among packets flows. As a result, in the past a few years, most of related works depended on the experiments and observations only. Based on the physical definition of time, IP covert timing channels are categorized as three types according to their different working methods. Furthermore, the mathematical models of IP covert timing channels of fixed-length time slots and inter-packets delays are built through the probability theory, respectively. In addition, the bandwidth function and error rate function of the network parameters for IP covert timing channels are derived. Experimental results show the correctness of the mathematical models as well as the theoretical analysis conclusions in the paper. The models of IP covert timing channels have formed a base on which some of researches in this area can be done through the formal analysis instead of the experimental observations only. Key wordsIP covert timing channel; information hiding algorithm; bandwidth; error rate; robustness 收稿日期:2015-01-22;修回日期:2015-04-28 基金项目:国家自然科学基金项目(61300228);江苏省科技支撑项目(BE2013103);江苏省科技成果转化项目(BA2015161);江苏省“六大人才高峰”高层次人才项目(1631170006);江苏大学拔尖人才项目(1213000013) 中图法分类号TP391 This work was supported by the National Nature Science Foundation of China (61300228), the Jiangsu Provincial Science and Technology Support Project (BE2013103), the Jiangsu Provincial Transformation Project for Scientific and Technological Achievements (BA2015161), the Six Industries Talent Peaks Plan of Jiangsu (1631170006), and the Talent Peak Plan of Jiangsu University (1213000013).