营造“动感地带”,激活学生发散性思维
——一道九年级数学竞赛题的解题教学与反思
2016-06-16浙江省宁波市鄞州区集士港镇中学许科挺
□浙江省宁波市鄞州区集士港镇中学 许科挺
营造“动感地带”,激活学生发散性思维
——一道九年级数学竞赛题的解题教学与反思
□浙江省宁波市鄞州区集士港镇中学许科挺
现在的解题教学,大多数还是以教师讲解为主,以总结概念、精讲例题来完成,这样的演绎体系存在种种弊端,如:(1)缺少调动学生情绪及进入学习角色的兴奋点,不利于学生学习兴趣的激发和求知欲望的发生和发展;(2)限制了部分学生的表现欲和成就感,不利于学生的人格发展和个性发展;(3)缺少小组合作,不利于全班团结合作能力的培养和智能水平的发展。那么,如何克服上述弊端呢?
教育家叶圣陶先生曾经说过:“教材只能作为教课的依据,而教得好,使学生得益,还得靠老师的善于运用。”这句话告诉我们,教学材料仅仅只是提供了最基本的教育资源,但并不是唯一的资源。数学教学应该是数学“思维活动”的教学,必须作为“思维过程”来进行。
下面就一道九年级竞赛题的解决,在探索与实践中让学生发散思维,从中积累数学经验,感悟数学思想方法。
一、案例呈现(发现问题,由“点”到“线”)
问题:如图1,已知五边形ABCDE中,AB∥ED,∠A= ∠B=900,则可以将该五边形ABCDE分成面积相等的两部分的直线有_____条,满足条件的直线可以怎样去确定:_____
让学生独立尝试几分钟后,我们就可以从学生的角度开始分析——
生1:可以将该五边形ABCDE分成面积相等的两部分的直线有1条,满足条件的直线可以这样去确定:如图2,延长BC、ED交于点F,将原五边形补成一个矩形,取该矩形的重心G,记△CDF的重心为H,直线GH即为所求。
复习基本图形的重心,提问:你知道哪些基本图形的重心?(学生开始讨论……)
生:线段的重心是该线段的中点,三角形的重心是该三角形三条中线的交点,平行四边形的重心是该平行四边形两条对角线的交点,梯形的重心是上下底中点连线与中位线的交点。
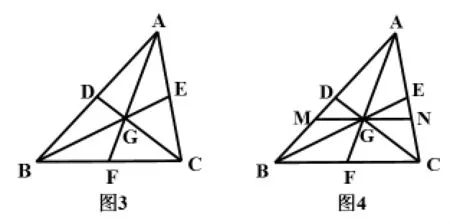
师反问:如图3,点G是△ABC的重心,过点G的任意一条直线都能将△ABC的面积平分吗?
(学生开始思考……过了一会儿)生2举手回答:不一定,如图4,过点G作MN∥BC分别交AB、AC于M、N,∵点G是△ABC的重心
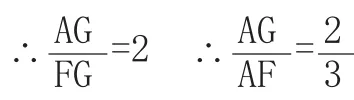
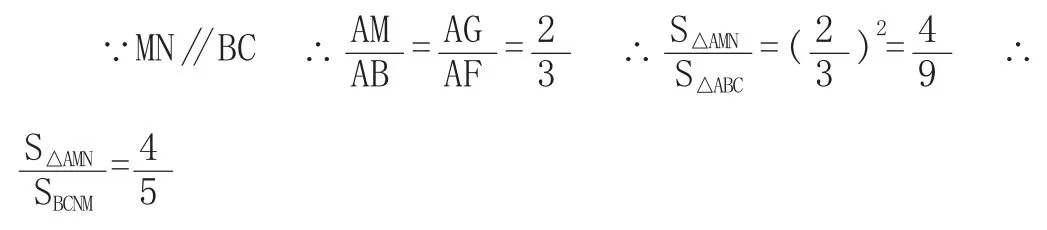
∴直线MN过点G,但不能将△ABC的面积平分。
师小结:同学们,对于有些结论,我们可以用特例来检验一下,比较直观。
师:同学们也可以发现,生1找到的直线GH是不一定能将五边形面积平分的。
我的意图是,给出生1的解答,让其他学生通过熟悉的知识找到生1解答中的问题所在,便于调动学生的积极性,同时也为后面的知识应用做铺垫。
师:同学们,我们发现:过三角形的重心,画一直线未必将三角形面积平分。那么,特殊四边形当中,是否也是如此呢?
生2马上有了答案:过矩形、菱形、正方形、梯形的重心,画一直线必将三角形面积平分。
老师投去了赞许的目光,其他学生也纷纷表示赞同。
师(趁热打铁):接下来,同学们对于原问题的解决有没有其他的点子呢?
生3(带着疑问):老师,能不能将五边形分割成一个矩形和一个直角梯形?
如图5,过C作AB的平行线CF,交AE于F,该五边形分割成一个矩形和一个直角梯形。
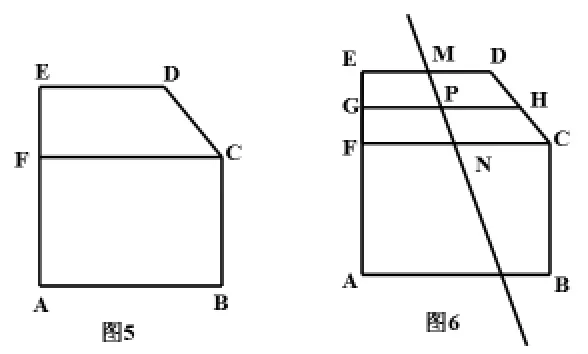
师:你讲得很好,请继续。
生3:我先画一条直线将直角梯形CDEF的面积平分。如图6,①取直角梯形CDEF的中位线GH,②取中位线GH的中点P,③过中点作一条直线与直角梯形两底边ED、FC分别交与M、N,直线MN即为所求。
师(追问):将直角梯形CDEF面积平分的直线有_____条呢?
生3:噢(好像突然有了灵感),可以将直角梯形CDEF面积平分的直线有无数条(非常高兴的)。
师:那么可以将该五边形ABCDE分成面积相等的两部分的直线有_____条,满足条件的直线可以怎这样去确定呢?
生3(有点请教老师的意思):可以将该五边形ABCDE分成面积相等的两部分的直线……(停顿了一下)好像只有1条,满足条件的直线可以这样去确定:如图7,过C作AB的平行线CF,该五边形分割成一个矩形和一个直角梯形,记矩形的重心为K,取直角梯形中位线GH,线段GH中点为J,直线JK即为所求。

师:生4好像有话要说,请(加了语气)。
生4迫不及待地说:可以将该五边形ABCDE分成面积相等的两部分的直线有无数条,满足条件的直线可以这样去确定:如图8,过C作AB的平行线CF,该五边形分割成一个矩形和一个直角梯形,记矩形的重心为K,取直角梯形中位线GH,线段GH中点为J,直线JK即为所求直线之一。设直线JK 与DE、AB分别交于M、N,取线段MN中点O,过点O且与DE,AB分别相交的直线均可将五边形面积平分。
笔者惊叹于生4的完美解答。我的想法是,没有预设,就没有教学;没有生成,就没有精彩!在解决问题中,我们既要让学生学会,更要让学生会学、乐学,一些解题的方法与策略需要教师在平时的教学中逐步渗透。一位好的教师会不断探索与实践,博采众长,独辟蹊径,运用全新的数学观念、创造性的思维方式、风趣幽默的教学语言,让学生在尽情领略数学“大自然”的美妙风光、亲身经历探求数学宝藏的发现活动中,思维能力悄然快速地提高。
而后,笔者让生5自行归纳解决本题过程中用到的知识点,重点强调了“等积变形”在此题的运用。
二、问题延伸(基于学生“最近发展区”的问题解决,由“线”牵动“面”)
心理学研究表明:学生对处于自己“最近发展区”的知识最感兴趣,对掌握主动权的学习最有积极性。于是在解决问题后,笔者将学生分成四大组,以组为单位让学生自行查阅资料,找到了相关的几道题。笔者摘录了其中三道题目。
⒈如图9所示,五边形ABCDE是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,现已变成如图10所示的形状,但承包土地与开垦荒地的分界小路(图10中折线CDE)还保留着。张大爷想过点E修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多,右边的土地面积与开垦的荒地面积一样多。请你用有关的几何知识,按张大爷的要求设计出修路方案(不计分界小路和直路的占地面积),要求说明方案设计理由,并画出相应的图形。
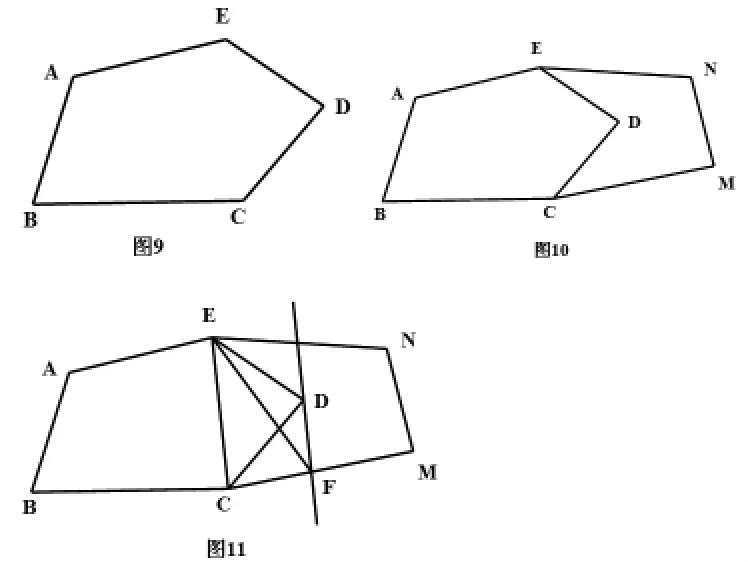
解:如图11,连结EC,过点D作DF∥EC交CM与点F,连结EF,线段EF即为所求直路。理由:∵DF∥EC∴S△EDC=S△EFC∴SAEDCB=SAEFCB
即直路修好后,要保持直路左边的土地面积与承包时的一样多,那么右边的土地面积与开垦的荒地面积也一样多。
⒉如图12,四边形ABCD中,∠B=900,,∠BCD=450,,AB=4,BC=5,,则△ACD的面积为。
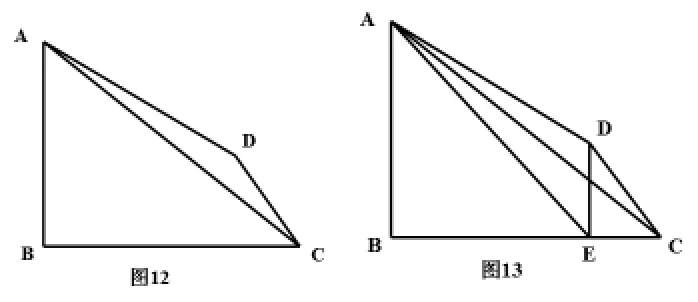
解:如图13,过点D作DE⊥BC于E,连结AE,
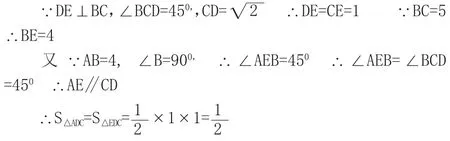
⒊如图14,n个正方形并排放在一起,其边长(从左到右)依次分别为a1,a2,…,an,则△ABC的面积为。
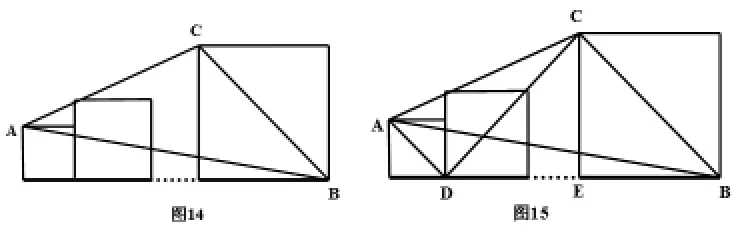
解:如图15,连结AD,CD,则AD∥BC,
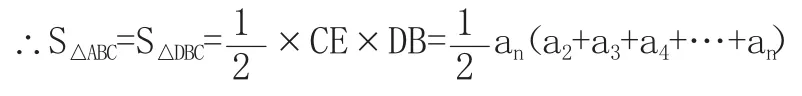
师总结:同学们,我们不缺少思维训练,但是数学知识“内化”才是同学们思维升华的关键、学习的根本。那么,如何做到这一点呢?我们就以上三题可将数学知识模块化,对于诸如此类面积问题的解决可归结为四种方法:

三、反思
初中数学的学习,总是伴随着一系列思维活动进行的。如果解题思路和方法能够独具一格,富有创造性,则能大大提高学生学习数学的效率,收到事半功倍的效果。
