经历思维挑战，从度性走向超越

2016-06-16江苏省苏州市吴江汾湖高新技术产业开发区实验小学王芳燕

新教育 2016年6期

关键词：白兔挑战条件

□江苏省苏州市吴江汾湖高新技术产业开发区实验小学　王芳燕

经历思维挑战，从度性走向超越

□江苏省苏州市吴江汾湖高新技术产业开发区实验小学王芳燕

【摘要】数学是思维的体操，学习数学离不开思维，没有数学思维，就没有真正的数学学习。本文从创设挑战机会、引领挑战过程、提升挑战经验三方面总结了一些平时训练和发展学生数学思维的教学方法。

【关键词】数学思维创设机会提升经验

数学是思维的体操，学习数学离不开思维，没有数学思维，就没有真正的数学学习。而现在的学生对于数学的学习缺乏一定的思考能力，只是老师教我怎么做我就怎么做，没有自己的想法，也不会在学习中发现问题、提出问题。这就需要我们教师在数学教学过程中特别重视和发展学生的好奇心，让每一个学生养成想问题、问问题、挖问题的习惯，让所有的学生都知道自己有权力和能力提出新见解、发现新问题，从而启迪他们的数学思维。

为了训练学生的数学思维，使学生的思维得到很好的发展，笔者在平时的课堂教学和习题设计中都考虑到了这一点，使用不同的教学方法让学生经历思维挑战，从度性走向超越。

一、创设挑战机会

人的大脑就像是一台机器，如果不使用它，不让它工作，就会“生锈”。学生在求学阶段就是要让他们处在思考问题的氛围中，不能都照着数学书本依样画葫芦地学一遍，而不对他们进行基本的思维训练。这就需要老师在教学中有针对性地使用教学方法，给学生创设思维挑战的机会。如教学三年级上册第一单元“笔算两、三位数乘一位数（进位）”时，由于前面已经学过几课时的三位数乘一位数，学生觉得列竖式计算没有一点难度，以为乘法计算就是简单的列竖式，学习上有些松懈。对于学生的这种情况我并没有多说什么，而是抛给他们一道题目，让他们尝试着做。

在□里填合适的数字。

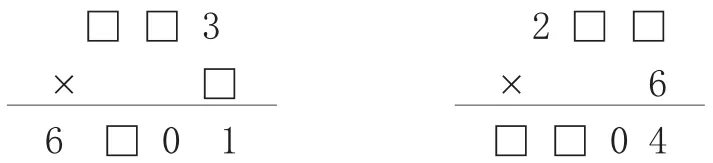
在适当的时候放手让学生挑战，不但能纠正他们学习上的陋习，而且也能有效培养他们的数学思维。如新授“长、正方形周长计算”一课，我并没有根据教材上的编排进行教学，而是利用一张长方形纸完成了整节课的教学。首先，学生根据手中的长方形纸计算出它的周长；然后通过折一折、剪一剪变成一个正方形和一个小长方形，计算正方形的周长；最后让学生动手折一折小长方形变成两个完全一样的图形，并计算出其中一个图形的周长。整节课学生的思维都处于兴奋状态之中，人人有动手操作、用眼观察、动口说理、动脑思维的机会，学生自己观察发现问题，积极探索得出结论，教学效果很好。

不同的知识用不同的教学方法，达到的是同样的效果——学生的思维得到了有效的发展。但是光给学生创造思维挑战机会是远远不够的，还要让学生亲自参与挑战的过程，在不同的练习中训练与培养他们的数学思维。

二、引领挑战过程

每个学生已有的认知水平不同，已有的数学思维也有所不同。因此在教学过程中要因材施教，要精心设计有层次、有坡度、要求明确、题型多变的练习题。教师要有的放矢地引领学生畅游在学习的海洋中，获取知识，发展思维。

1.引领学生经历不同的思维挑战。每个学生之间存在个性差异，对新知的接受能力各有不同。考虑到这些，教授不同的知识时注重通过不同的教学方法和教学手段引领他们经历不同的思维，才能在潜移默化中使数学思维深入他们心中。

第一，数学语言的训练，促进思维发展。语言是思维的表达方式，学生借助语言思考问题，表达思想。在数学课堂教学中，语言是师生、生生间情感交流、数学思维的工具。鉴于此，我十分注重训练学生的数学语言表达能力。如教材中出现的“观察上表，你有什么发现？”“你还能提出什么问题？”等这些带有思考性、较为开放的问题，我会给学生充分发言的机会，意在训练他们用确切的、完整的、简练的、清晰的数学语言来表达思维的结果。

第二，习题练习，发展数学思维。针对学生平时的练习情况，精心设计每周一练。每周一练上的题目都是学生易错的题，是一些基础知识，全班学生都需要掌握的。另外还设计了一道拓展题，让不同层次的学生都能有所得。对于练习题的训练我主要从以下方面进行：（1）读一读。任何数学题目的解答，必须先通过读题来了解题目所提供的信息和条件，然后才能有的放矢地运用所学知识去解决问题。因此，我要求学生在做题时先把题目认认真真读一遍，了解题目的基本信息，做到心中有数。（2）找一找。找出题目中最能体现解题范围或解题方法的关键词。（3）想一想。题目提供给了我们哪些知识的信息，从这个信息中你想到了可以用哪个学过的知识点来解决？这只是培养了学生思维的严密性，学生对问题的思考都有一种习惯趋势，遇到问题时往往会按照以前固定的思路去思考，这就是思维定势。但在解决问题的过程中，依照以往的方法去思考问题，有时会困难重重。但当我们转换思考问题的角度，从问题的反面去剖析、理解、推理、设想问题时，问题会简单化，这就是逆向思维。

第三，培养逆向思维。逆向思维在解决数学问题中，常常会遇到，因此，注重培养学生的逆向思维，有助于提高学生的思维水平。但在训练中发现学生思考问题时会自然而然地显现出固有的思想（照本宣科书上的知识），不会灵活变通。同类型的题目老师讲过后会解，但是变换一种说法或问法，他们又丈二和尚摸不着头脑了。这就需要我们老师在运用题量训练时还要注重方式方法，给学生一片广阔的天地，给他们一个自主的空间，让他们的数学思维能力在课堂学习中得到充分的发展。

2.引导学生由相对封闭走向开放。老师教什么学生就学什么、用什么，会迁移，但不会类推；思维较为狭窄，只知其一，不知其二，稍有变化，就不知所云。老师可通过开放性习题引起学生思维的发散，由封闭走向开放。如：黑兔12只，白兔3只，一共有多少只兔？我是这样引导学生的：黑兔的只数、白兔的只数，题目中都直接给出，我们称这两个条件是直接条件，所以一步计算：12+3=15（只）。如果题中第一个条件黑兔12只不变，那么第二个条件白兔3只与黑兔12只有什么关系？（学生会说：白兔3只比黑兔少9只……）如果题中“白兔3只”这个条件不直接给出，根据与黑兔的关系说出来，该怎样叙述题中的第二个条件？（学生可以答出：白兔比黑兔少9只……）解决问题需要知道白兔和黑兔的只数，白兔这个条件需要我们通过与黑兔的关系先算出来，白兔这个条件没有直接给出，这叫间接条件。谁还能把这个条件再变换一下说法，使它变成间接条件？（学生回答：黑兔比白兔多9只，黑兔是白兔的4倍……）学生思维活跃了，想方设法说出更新颖的条件。这样他们在积极思维中理解了什么是间接条件，间接条件与已知条件、问题的关系等。理解了也就自然会运算了。接着，我又让学生将第一个条件变成间接条件，第二个条件、问题都不变，或问题随着其中的一个条件同时改变，目的仍是巩固练习两步应用题，教给学生了解问题、分析问题、解决问题的思路，使学生掌握了解两步应用题的方法，解放了思考方式，发散了数学思维。

在独立解题中，学生的思维还没得到完全发展，想象力较差，所以光注重训练还不够，还必须在实际运用中不断提升自身的经验。