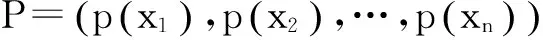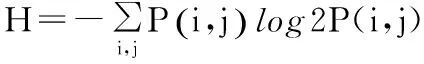基于改进EEMD和香农熵的铣刀磨损状态监测研究*
2016-06-16何栋磊
何栋磊,黄 民
(北京信息科技大学 机电工程学院,北京 100192)
基于改进EEMD和香农熵的铣刀磨损状态监测研究*
何栋磊,黄民
(北京信息科技大学 机电工程学院,北京100192)
摘要:为了分析铣削加工中复杂的声发射信号和克服EMD方法的模态混叠缺陷,在原始集合经验模态分解(EEMD)的基础上,提出一种改进的EEMD方法应用于铣刀磨损的状态监测。通过引入白噪声准则和中值滤波优化EEMD的算法,并基于香农熵从分解得到的IMF分量中提取有效分量,剔除虚假分量。最后将有效IMF分量的能量作为特征向量输入支持向量机(SVM)分类器来识别铣刀的磨损状态。经过在立式铣削加工中心上进行实验,结果表明此方法在识别铣刀磨损状态方面具有更高的准确性。
关键词:铣刀磨损状态监测;集合经验模态分解;白噪声准则;香农熵
0引言
在切削过程中,刀具与工件、切屑剧烈摩擦,不可避免的会产生刀具磨损和破损,若继续加工会直接降低产品的加工质量和生产效率。因此,采用适当方法建立精确可靠的刀具磨损状态监测系统对于提高加工精度和产品效益具有重要意义。目前,在刀具状态监测领域针对车削等连续加工方式的研究在理论和实践应用中取得了丰硕的成果,而对于断续加工方式下刀具磨损状态监测的研究理论准备不足,实用可靠性较低。铣削是多齿断续切削,切削过程中有多个刀刃参与加工,每旋转一周,铣刀上的一个刀齿仅工作一段时间,切入切出时易引起冲击振动。由于铣削过程不连续,导致铣削刀具状态信号较复杂,包含大量干扰因素,难以提取与刀具磨损状态相关的特征向量,因此铣刀磨损状态监测更为困难。针对铣削加工特点,选择灵敏度高和抗干扰性强的声发射传感器监测铣刀磨损状态。声发射(AE)信号是刀具切削过程中产生的一种高频弹性应力波信号,非常适用于检测刀具微小面积的破损和破损前产生的微裂纹,受刀具几何参数和切削参数的影响较小。但是,铣刀磨损过程中的AE信号是非线性、非平稳信号,需采用时频分析技术进行分析处理。经验模态分解(EMD)是一种基于Hilbert-Huang变换的自适应时频分析方法[1],将复杂的多分量信号分解成一组从高到低频带自适应划分的本征模态函数(IMF)之和,能够内在的描述原始信号的特征信息。但是,EMD的最大缺点之一就是模态混叠问题[2],即同一个IMF分量含有全异尺度或两个不同的IMF分量具有相同尺度。为了降低EMD的模态混叠,Wu Z.H.和Huang N.E.提出了集合经验模态分解方法(Ensemble Empirical Mode Decomposition,EEMD)又称噪声辅助经验模态分解方法[3],能够自动消除模态混叠问题。参考EEMD方法在刀具磨破损识别中的研究成果[4],并结合铣削加工方式特点,提出一种改进的EEMD方法对铣削AE信号进行分解,然后基于香农熵从所有本征模态函数之中提取与铣刀磨损状态密切相关的特征向量,最后输入支持向量机(SVM)识别铣刀的磨损状态。
1AE信号的采集
本实验在大连机床厂生产的VDL600立式铣削加工中心上进行;选择R15A型声发射传感器,安装在工件上;采用PAC公司的PCI-2型声发射信号分析仪器采集AE信号,采样频率为2MHz,选择2/4/6-AST型前置放大器,增益为40dB。根据刀具后刀面磨损量(VB)不同,实验分成正常磨损(VB<0.2mm),中期磨损(0.2
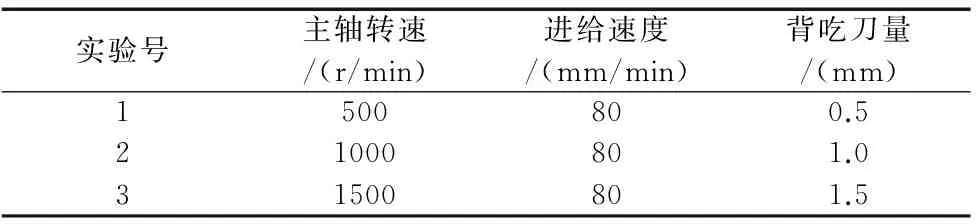
表1 实验切削参数
2集合经验模态分解(EEMD)
EMD方法的原理是在原信号中多次加入幅值不同的白噪声,利用白噪声频谱均匀分布的特点,使信号在不同尺度上具有连续性,且由于零均值噪声特性,经EMD分解求集合平均后噪声将相互抵消,从而克服模态混叠,得到更好的分解效果。
2.1原始EEMD的算法步骤
(1)初始化加入的高斯白噪声幅值标准差比值系数k和总体平均次数M,并令i=1;
式中:k为加入白噪声标准差与信号标准差的比值。
(4)重复步骤(2)和(3),每次加入不同幅值的白噪声序列,直到进行M次为止。构成IMF的集合为:
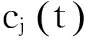
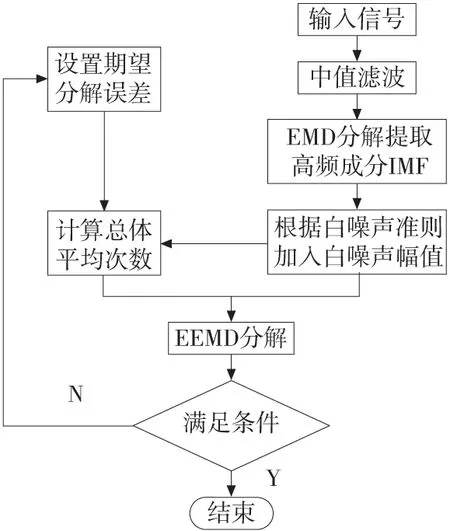
2.2EEMD的算法优化
在EEMD算法中,最重要的步骤是确定加入的白噪声幅值标准差比值系数k和总体平均次数M。其中,加入的白噪声幅值影响信号极值点分布均匀性和EEMD的分解精度。若加入的白噪声幅值过小,不能有效解决模态混叠问题;若加入的白噪声幅值过大,则会产生很多虚假的IMF分量。通常,取k值为0.2,对于以高频为主的信号,适当减小白噪声幅值;以低频为主的信号,则适当增加白噪声幅值。
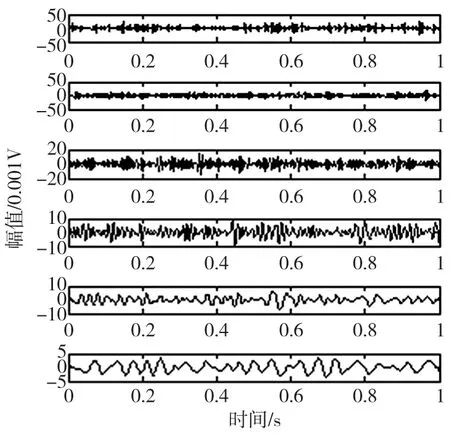
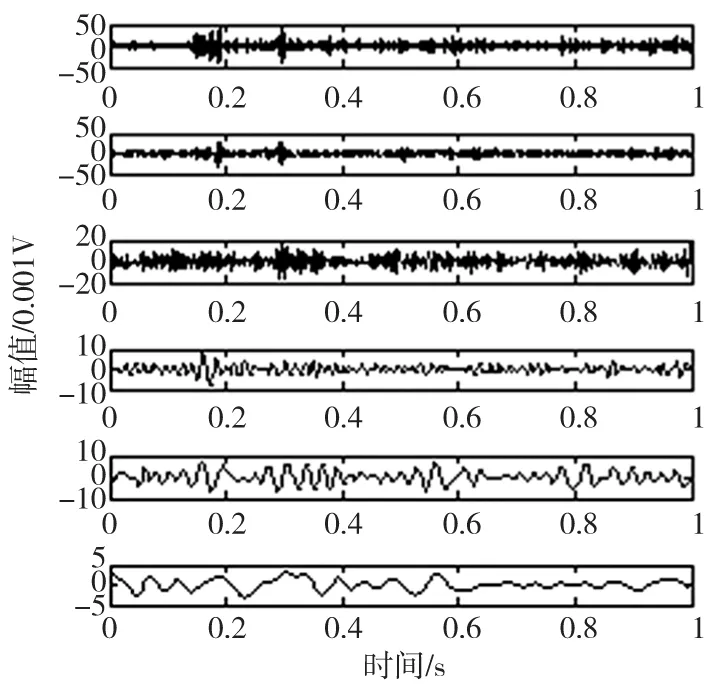
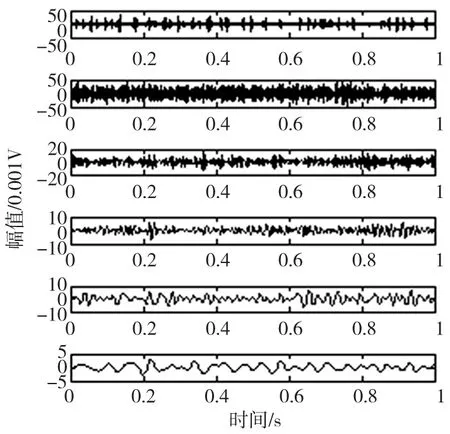
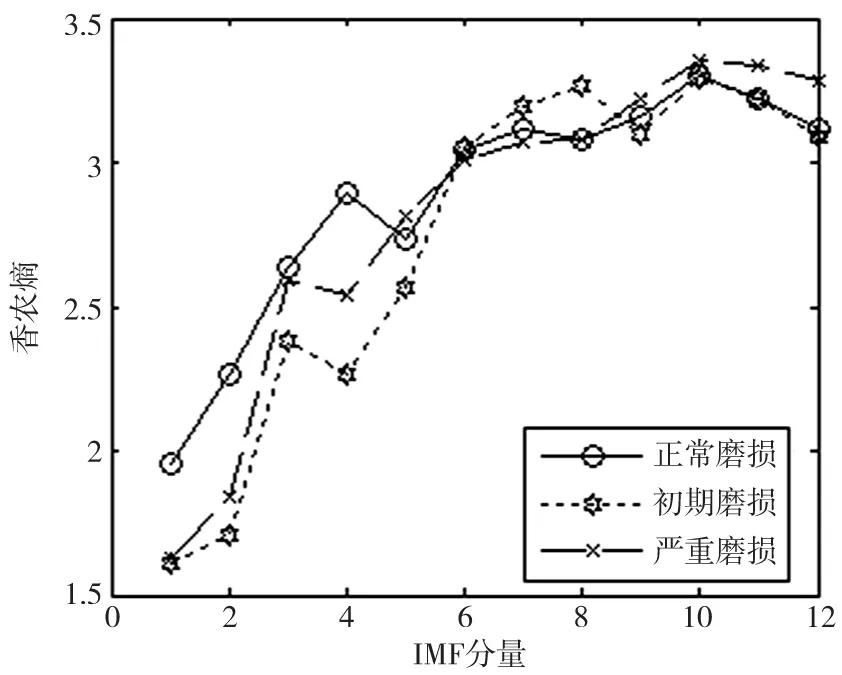
根据EEMD方法中加入白噪声的准则[5-7],确定加入白噪声的幅值范围:
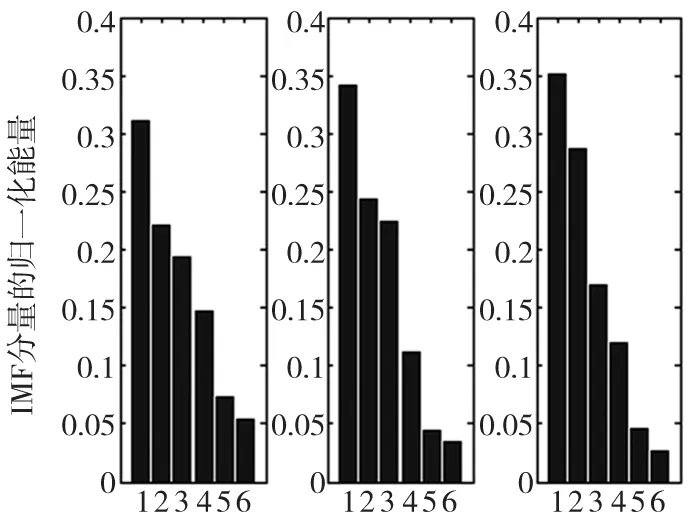
0 式中:k为加入白噪声幅值标准差σn与原始信号幅值标准差σ0之比,即k=σn/σ0;X为信号中高频部分的幅值标准差σh与原始信号幅值标准差σ0之比,即X=σh/σ0;由此可得加入白噪声准则的等价表达式为: 0<σn≤σh/3 在上述的加入白噪声准则中,先需要确定原始信号的高频成分。通常用EMD提取IMF1作为原始信号的高频成分,但在背景噪声较大,干扰因素较多的场合,经过EMD分解后的IMF1中存在模态混叠,影响加入白噪声准则的可靠性。因此对原始信号先进行中值滤波,以提高信号的信噪比。中值滤波是基于排序统计理论的一种非线性的平滑滤波技术,能够滤掉脉冲干扰,具有良好的边缘保护特性[8]。 总体平均次数M大小决定了对于信号中加入的白噪声的消除效果。通常总体平均次数越大,则加入的白噪声对于分解结果的影响越小。当设定期望分解误差e值(输入信号与EEMD分解后所有IMF之和的相对误差)后,根据Wu Z.H.提出的关系式可自动获得总体平均次数M,即: 改进的EEMD算法流程图如图1所示。 图1 EEMD改进算法流程图 在切削条件3下,不同磨损程度的AE信号经改进的EEMD方法分解后分别得到14个IMF分量,前6个IMF分量的分解结果如图2~图4所示。 图2 正常磨损程度下AE信号的EEMD分解结果 图3 中期磨损程度下AE信号的EEMD分解结果 图4 严重磨损程度下AE信号的EEMD分解结果 3基于香农熵的特征向量提取 提取与刀具磨损状态密切相关的特征向量直接关系到诊断结果的准确性。EEMD方法作为一种自适应的分析方法,适用于非线性、非平稳信号的处理,将刀具信号分解为一系列本征模态函数(IMF)的组合,包含了不同频率尺度下的信息。其中,IMF分量的能量是刀具磨损状态最重要的参考指标。当刀具发生磨损时,刀具信号的能量随着频率的分布结构而变化。通常直接把前几个IMF分量作为特征向量,但选取数量无依据。或利用相关系数法提取所有IMF分量中与原始信号的相关系数大的作为特征向量。但是,若原始信号幅值远大于IMF分量的幅值,则其相关系数会很小,易造成误判。 1948年,信息论之父香农(Shannon)在《通讯的数学理论》中提出了香农熵的概念,泛化了熵的含义,使信息论得到了更广泛的认知和应用[9]。基于香农熵的概念,提出利用香农熵值和IMF分量的关系来筛选出有效的IMF分量。 香农熵能够描述系统的不确定程度。当概率分布P的不确定性越大,其熵值就越小;反之,当概率分布P越确定,其熵值就越大。由于时频分布与概率分布具有相似性,则通过计算香农熵可以分析信号时频分布的聚集性,见下式: 声发射信号经过EEMD分解后,得到一组不同带宽和频率的IMF分量,且这些IMF分量会随着信号的变化而变化。根据香农熵的定义,如果IMF分量中含有大量的刀具磨损故障信号信息,则其时频分布的聚集性就会越集中,对应的熵值就会越小。如果IMF分量的时频分布越差,其熵值就越大,此IMF分量中包含故障信号信息的可能性就越小。 根据三种磨损程度下所有IMF分量的香农熵值,得到IMF香农熵值曲线,如图5所示。 图5 IMF分量的香农熵值曲线 原始信号经EEMD分解为12个IMF分量,其中,IMF1~IMF6的香农熵较小,其时频分布的聚集性更强,其所包含的刀具磨损状态信息较丰富。而IMF6~IMF12的香农熵较大,其所包含的信号的不确定性比较大,故视为虚假分量予以剔除。 因此,特征向量的提取步骤为: (2)计算各IMF分量的香农熵值进行比较,筛选出m个时频分布聚集性高的IMF分量; (3)求每个IMF分量的能量Ei: (4)求原始信号的总能量E: 其中:pi=Ei/E,为第i个IMF分量的能量占信号总能量的比值,i=1,2,…,m (6)将向量T′作为最终的特征向量输入支持向量机分类器。 经过筛选后,三种磨损程度下前6个IMF分量的归一化能量如图6所示。 图6 IMF分量的归一化能量图 从图6可以看出,在正常磨损状态下,由于刀具切削表面规整,AE信号能量主要集中在IMF1中。随着刀具磨损程度增加,IMF2和IMF3频带的能量逐渐增加,而IMF4~IMF6频带的能量会减小。因此当刀具出现磨损甚至破损时,整个IMF分量的能量分布结构会调整,高频分量的能量明显增加,而低频分量的能量逐渐减小。 4铣刀磨损实验 在不同的切削条件下进行刀具铣削实验,采集铣刀三种不同磨损状态的AE信号。每种状态采集40组数据,选择其中20组作为训练样本,另外20组作为检验样本,即共60组训练样本和60组检验样本,先将训练样本输入支持向量机(SVM)建立刀具磨损状态识别模型,然后将检验样本输入模型中测试该模型的分类准确率。 SVM是根据结构风险最小化原则建立的模式识别方法,特别适用于小样本,非线性,高维数等分类情况[10]。本文选择核函数为RBF(径向基)函数三分类SVM分类器,对应标签分别为正常磨损—1,初期磨损—2,严重磨损—3。经过计算,其分类准确率为93.2%。另外,采用原始的EEMD方法和EMD方法提取特征向量,输入支持向量机后,分类准确率分别为91.6%和87.1%,如表2所示。经过对比,改进的EEMD方法取得了更好的分类效果。 表2 应用不同提取方法的检验样本分类结果 5结论 针对铣削的多齿断续加工方式,通过改进的EEMD分解后得到更平稳的IMF分量,不仅克服了EMD的模态混叠缺陷,而且增强了原始EEMD的自适应性。另外,本文根据香农熵提取特征向量,筛选出有效的IMF分量,使这些分量与刀具磨损类故障的联系更加密切,从而能够提高刀具磨损状态的识别成功率,做出更准确的诊断。 [参考文献] [1] N E Huang, Shen Z S R Long, The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc.R.Soc.London,1998,454:903-995. [2] 胡爱军,孙敬敬,向玲. 经验模态分解中的模态混叠问题[J]. 振动.测试与诊断,2011,31(4):429-434. [3] Wu Z H,Huang N E. Ensemble empirical mode decomposition: A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis,2009(1):1-41. [4] 杨明伦,邵华. 基于EEMD和IMF能量分布的刀具破损识别[J]. 组合机床与自动化加工技术,2013(4):54-58. [5] 魏永合,王明华,林梦菊,等. 基于改进EEMD的滚动轴承故障特征提取技术[J]. 组合机床与自动化加工技术,2015(1):87-90. [6] 蔡艳萍,李艾华,徐斌,等.集成经验模态分解中加入白噪声的自适应准则[J].振动、测试与诊断,2011,31(6):709-714. [7] 陈艳娜. 基于EEMD的旋转机械故障诊断方法研究[D].哈尔滨:哈尔滨理工大学,2013. [8] 刘颖,陈谨女. 自适应中值滤波算法在图像处理中的应用[J]. 物联网技术,2013(3):51-52. [9] 杨雪特. 熵的引入、深化与泛化——从克劳修斯熵到香农熵[J].内江师范学院学报,1991(4):62-65. [10].王姣,刘海燕.基于支持向量机和遗传算法的刀具故障诊断[J].组合机床与自动化加工技术,2013(1):74-76. (编辑赵蓉) Research of Tool Wear Monitoring Method Based on Modified EEMD and Shannon HE Dong-lei, HUANG Min (School of Electromechanical Engineering, Beijing Information Science & Technology University,Beijing 100192,China) Abstract:For the complex acoustic emission signals in milling process and modal aliasing defects of EMD method,a new approach based on original ensemble empirical mode decomposition(EEMD) was proposed to achieve the detection and identification of tool wear in milling process.Through introducing white noise criteria and median filter to optimize the algorithm of EEMD.Then extracting effective intrinsic mode functions(IMFs) and excluding false functions according to Shannon.At last,the energy of effective IMF functions are taken as inputs of support vector machine(SVM) classifier to identify the state of cutter. After experiments on vertical milling centers,the results showed that this method could more accurately identify the tool wear. Key words:tool wear monitoring; EEMD; white noise criteria; shannon 文章编号:1001-2265(2016)05-0075-04 DOI:10.13462/j.cnki.mmtamt.2016.05.020 收稿日期:2015-07-12;修回日期:2015-08-08 *基金项目:国家科技重大专项资助项目(2013ZX04011-012) 作者简介:何栋磊(1989—),男,回族,北京人,北京信息科技大学硕士研究生,研究方向为机电系统状态监测与故障诊断,(E-mail)hdlmail@126.com;通讯作者:黄民(1965—),男,江苏徐州人,北京信息科技大学教授,博士,研究方向为机电系统状态监测与故障诊断,(E-mail)Hm_cumt@sina.com。 中图分类号:TH165;TG501 文献标识码:A