双驱进给系统热误差仿真分析及试验*

夏阳雨，程　寓，倪玉晋，缪海俊

(南京理工大学 机械工程学院，南京　210094)



双驱进给系统热误差仿真分析及试验*

夏阳雨，程寓，倪玉晋，缪海俊

(南京理工大学 机械工程学院，南京210094)

摘要：为了研究双驱伺服进给系统热变形对双丝杠不同步误差的影响，建立了有限元仿真模型。分析了进给系统稳态温度场，通过改变电机转速，分析在不同进给速度下系统达到热平衡的时间和其热变形，得到了双丝杠不同步误差变化规律。使用Renishaw激光干涉仪测得MCH63试验台在不同转速下不同步误差的变化情况，同时将试验结果与有限元分析结果对比。仿真与试验结果表明：双驱结构易造成温度场分布不均而产生不同步误差；随着电机转速的增加，双丝杠达到热平衡时其温度差和不同步误差也会增加。有限元仿真和试验的增幅差值在14%以内，并呈现波动减少的趋势，说明有限元建模和分析的可靠性。因此，该研究可为预测双丝杠进给系统不同步误差提供一种可行的方法。

关键词：双驱进给系统；热变形；温度场；不同步误差

0引言

双丝杠驱动进给系统作为数控机床的关键组成部分，由于其具有提高系统刚度、抑制系统振动以及提升系统响应等优势，越来越多的应用于实际生产当中[1-3]。但是双丝杠的不同步误差会极大的影响加工精度。而对于高精数控机床，热误差约占机床总误差的70%[4]。热变形是影响双丝杠不同步误差的关键性因素。

现有的不同步误差研究多为对双丝杠控制系统的研究，关于机械部分热变形对不同步误差的影响研究很少。陈瑶，赵万华等人对动式龙门机床的双驱同步控制系统建模，分析了进给系统不同步误差和误差补偿[5-7]。Min等人以傅里叶热力学方程为基础，建立了包含多种边界条件的热态模型，并分析了不同热流密度下丝杠温度场梯度的分布特性[8]。Wu等人通过有限元方法和仿真与试验相结合的方法，分析了预紧力及进给速度与丝杠温度场，热变形的相关关系[9]。但是对于热变形对进给系统不同步误差的影响研究文献很少见到。

本论文以双丝杠直线进给系统作为研究对象，从滚珠丝杠螺旋副的生热差异出发，基于有限元法对热变形引起的双丝杠不同布误差进行仿真建模分析，并通过实验验证，进一步说明有限元建模和分析的可行性。

1仿真分析

1.1稳态温度场

将三维模型导入到ANSYS中，进行单元类型的选取，选择八节点六面体的solid70；其次，进行网格划分，通过定义接触对模拟结合面之间的热量传递。再次，计算边界条件，由于机械结构以及散热条件等因素不尽相同，两根丝杠的发热量必然会不完全相同，此处只考虑丝杠发热量不同，以转速为1000r/min为例，根据公式计算出进给系统的发热量作为边界条件。最后，进行进给系统的稳态温度场及热-结构耦合分析。

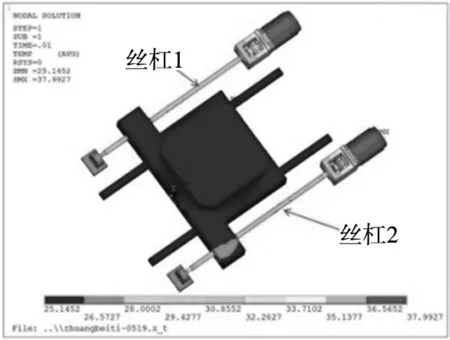
图1　稳态温度分布

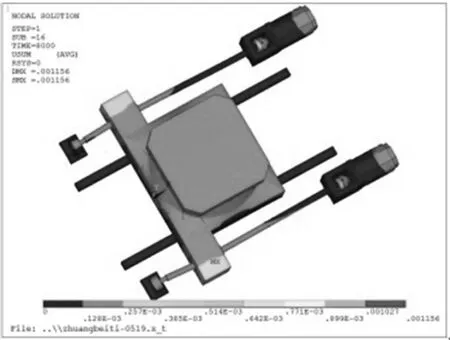
图2　系统热变形

从进给系统稳态温度分析结果发现，进给系统主要是在电机、轴承以及滚珠丝杠副等处温度较大；滚珠丝杠主要是在两端与轴承连接处温度较大。从热-结构耦合分析结果可知，进给系统的各个零部件的位移变化都不尽相同，其中变形较大的是螺母和丝杠结合面处，由此导致工作台在运行过程中会发生扭转从而产生不同步误差。

1.2不同电机转速下系统热变形

根据试验条件，分析了转速为100，200，300，400，500，600r/min时，进给系统的温度以及热变形的变化规律，如图2所示，其中温度较高的曲线表示丝杠2的温升变化规律，温度较低的曲线表示丝杠1的温升变化规律。

由图3、图4可知，从各个转速条件下达到热平衡时的温度分布可以发现，随着转速的上升温度也在不断的上升。当电机转速增加时，丝杠1和丝杠2达到热平衡时的温度差也逐渐呈现扩大趋势。分别提取丝杠1和丝杠2观测点处的22个节点数据的平均值作为分析对象，并求出其差值，就是丝杠这两个观测点的不同步误差，从图5可以看出随着转速的增加，其不同步误差也在相应的增加。

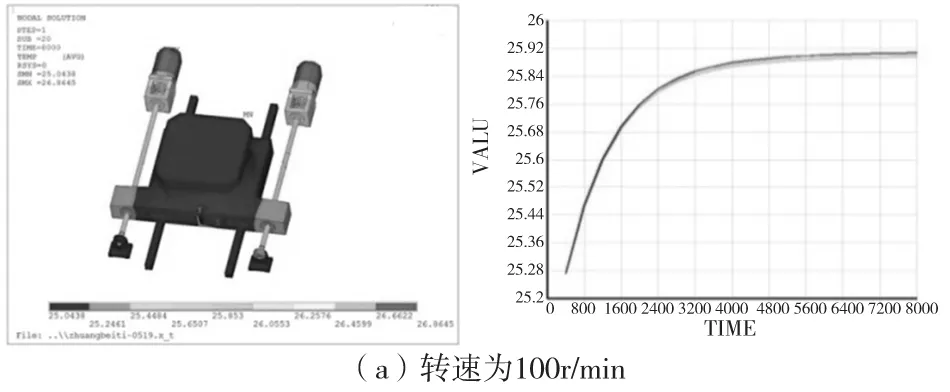
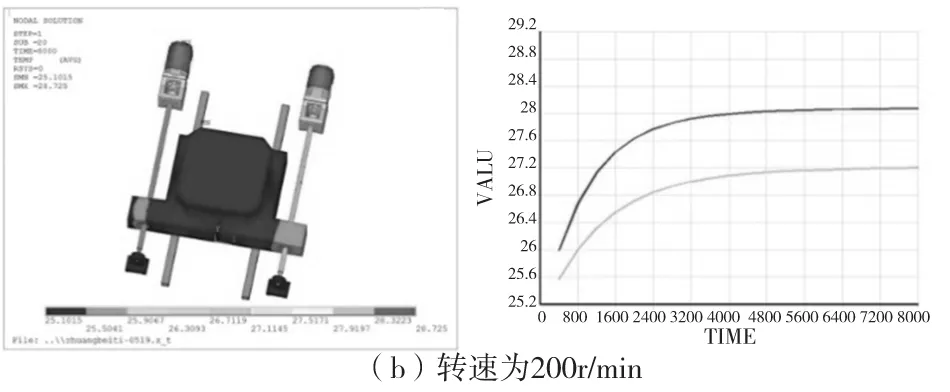
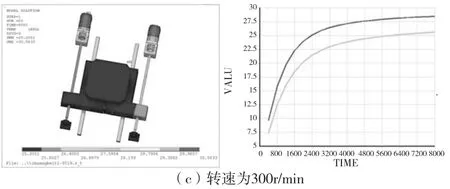
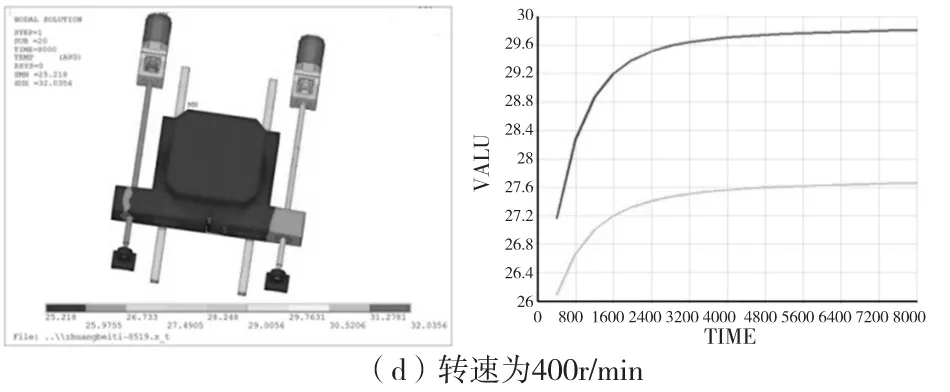
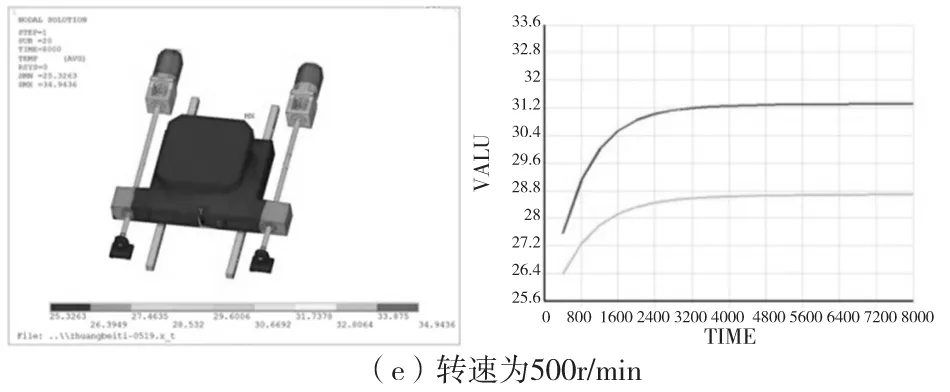
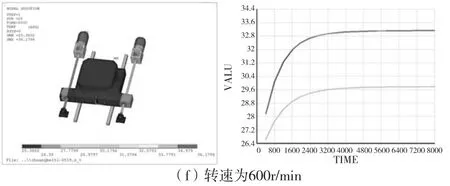
图3　瞬态温度场分布及温升曲线

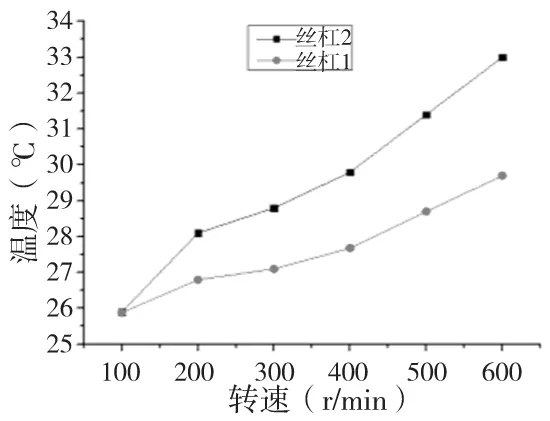
图4　热平衡时的温度变化趋势

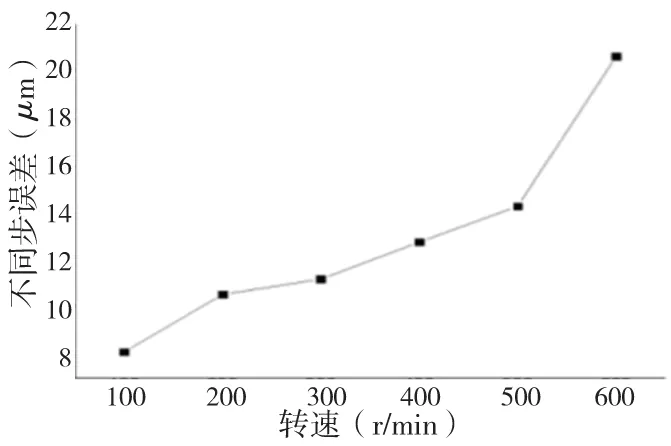
图5　转速变化引起的不同步误差

2热变形引起不同步误差的实验验证

基于Renishaw激光干涉仪测得MCH63试验台丝杠螺母副测试点处的热变形分布规律。再次，测得不同转速下的不同步误差变化情况。最后将试验热变形与有限元分析结果对比，说明有限元建模和分析的可靠性。

2.1实验系统

结合Renishaw XL激光测量系统，搭建起测量几何尺寸的系统，包括进给系统、XL激光头、镜组以及XC补偿单元和传感器，连接方式如图6所示。

图6　测量系统连接图

2.2进给系统热变形的测量

为了验证进给系统温度变化对零部件位移影响规律的正确性，测量了丝杠螺母副处热变形的变化规律，选择测试系统中干涉镜位置为测试点，进行了42次试验，每次试验又测量了3次往复运动的位移误差。为了减少环境温度对试验数据的影响，本试验是在室温恒定在25℃时进行测量的。

表1为电机转速分别为100r/min、200r/min、300r/min、400r/min、500r/min及600r/min，运行时间为30min、60min、90min、120min、150min、180min和210min时的位移误差。

随着进给系统工作台的运行，测量点处的位移误差逐渐增加，这主要是因为随着运行距离的增加，位移误差出现了累积的现象。

通过激光干涉仪的材料温度传感器可以读取测量点的温度，并统计测量点处的温度变化情况，如图7所示。同时，为了得到实际测得的位移误差，需要将表1中测得的数值都减去重复定位精度，就得到了测量点的实际位移误差，如图8所示。

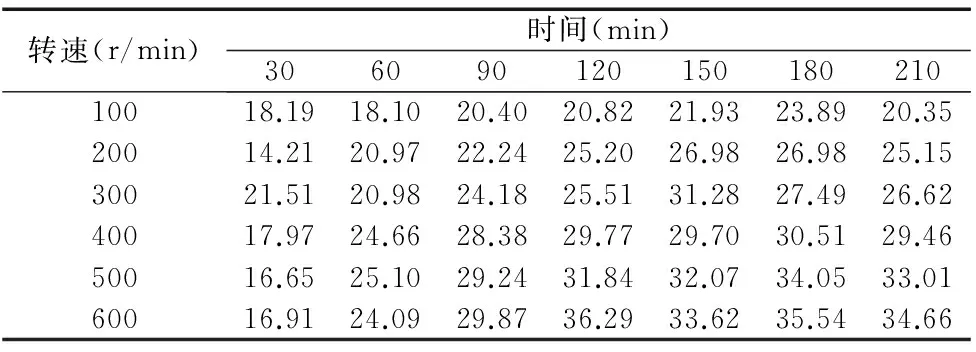
表1　测试点处位移误差

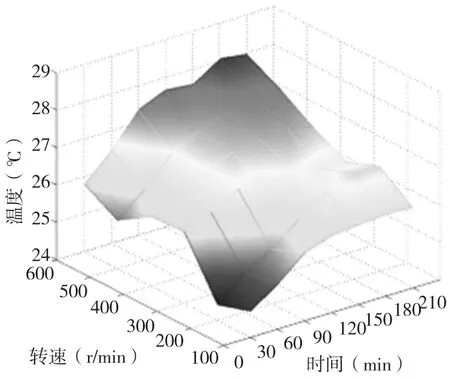
图7　测量点温度变化

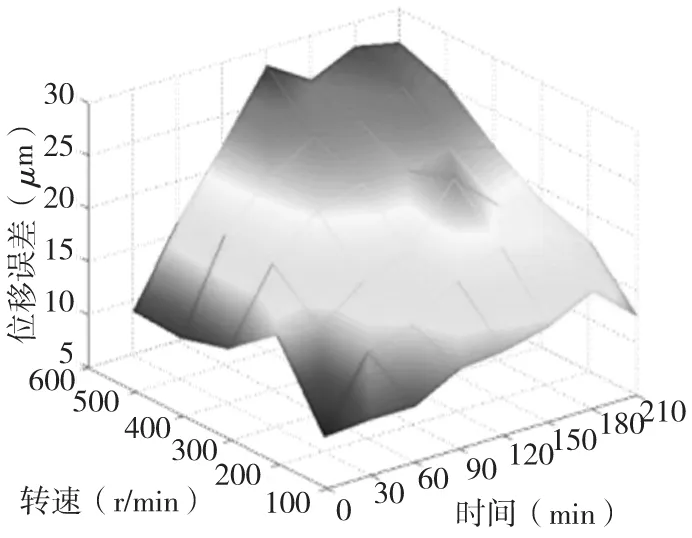
图8　测量点实际测量位移

从图7中可以看出，随着时间的增加，一开始温度上升的很快，渐渐的温度变化趋于平缓，6次试验大约在2.5h左右达到热平衡。随着转速的增加，热平衡时的温度呈现明显的增加。从图8中看出，随着时间的增加，测量点热变形的数值呈现上升趋势。随着转速的增大，测量点的温升变化逐渐增加，可见随着转速和运行时间的增加，热变形呈现明显的变化。

2.3双丝杠进给系统不同步误差的测量

进给系统的不同步误差的测量原理，如图9所示，由于工作台的扭转角度θ较小，扭转角度θ近似于sinθ，故

其中：D为测试出的双丝杠之间的位移差；2L为双丝杠轴心之间的距离。所以，当测出工作台的扭转角，就可以间接计算出双丝杠的不同步误差。

本文测了电机转速分别为100r/min、200r/min、300r/min、400r/min、500r/min及600r/min，运行时间为30min、60min、90min、120min、150min、180min和210min时的扭转角变化情况，如图10所示。

图9　不同步误差测量原理

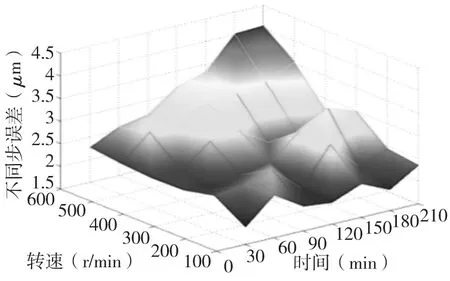
图10　测量点扭转角变化

从图10中可以看出，随着运行时间和电机转速的增加，不同步误差呈现上升趋势。从三维图形中可以十分直观地看出，随着运行时间和电机转速的增加，尽管不同步误差会出现些许波动，但是总体上不同步误差呈现不断上升的趋势。

2.4试验热变形与有限元分析热变形对比

为了验证仿真结果的正确性和可靠性，将有限元仿真的结果和试验分析的结果进行比照验证，根据有限元仿真结果和试验分析的不同步误差进行对比，如表2所示。

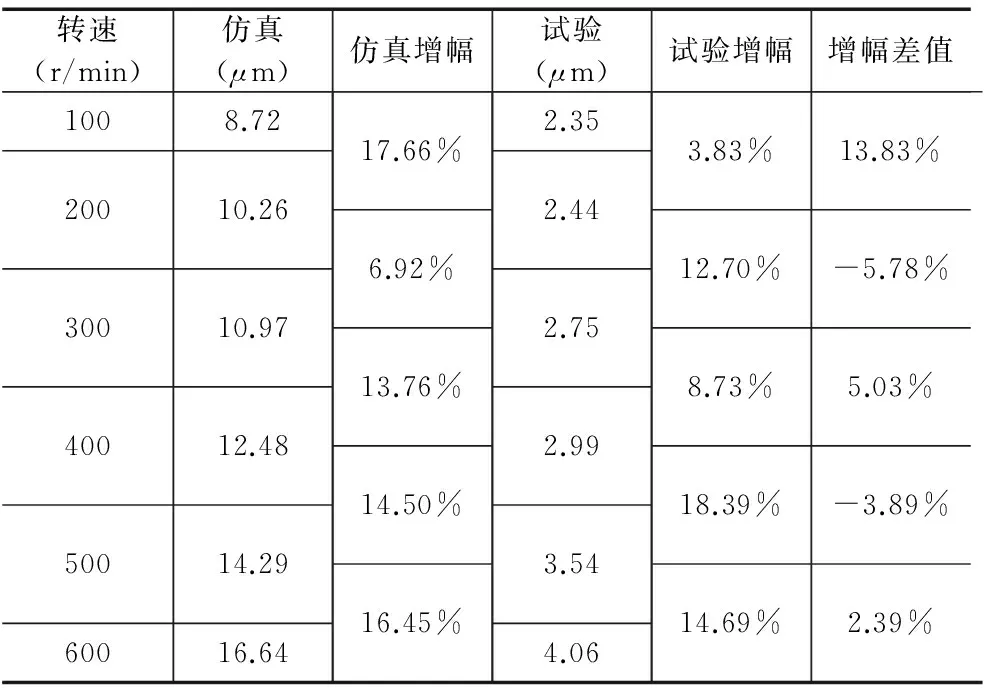
表2　有限元仿真和试验的不同步误差对比

综合以上6组分析对比，有限元仿真和试验的增幅基本都是在3%～19%之内。说明有限元建模和分析的可行性。

3结 论

通过对MCH63试验台双驱进给系统进行热态仿真分析及试验，测试了稳态温度场和不同进给速度下热变形和不同步误差变化规律，得到以下结论：

(1)随着进给系统工作台的运行，测量点处的位移误差逐渐增加，这主要是因为随着运行距离的增加，位移误差出现了累积的现象。

(2)进给速度增大，摩擦生热增大，从而导致丝杠膨胀加剧，使得热误差随之增大，随着运行时间和电机转速的增加，不同步误差会出现些许波动，但是总体上呈现上升趋势。

(3)热平衡时温度随进给速度的增大而增大。系统达到热平衡后，不同步误差呈现平缓趋势。所以在设计分析中，只需要考虑当转速和达到热平衡时间的极限条件下，将不同步误差控制在允许范围内，就可以满足生产设计的需求。

[参考文献]

[1] Hiramoto K，Hansel A，Ding S．A Study on the Drive at Center of Gravity(DCG) Feed Principle and its Application for Development of High Performance Machine Tool Systems [J]．CIRP Annals Manufacturing Technology，2005，54(1): 333-336.

[2] Mori Seiki Co., Ltd. Machine Tool Driven by Center of Gravity[J]．Seisanzai Maketeingu，2005.

[3] Kamalzadeh A，Erkorkmaz K．Accurate tr-acking controller design for high-speed drives[J]．I-nternational Journal of Machine Tools and Manufa-cture，2007，47(9): 1393-1400.

[4] Chao Jin, Bo W, Y M Hu. Heat generate-on modeling of ball bearing based on internal load distribution[J]. Tribology International, 2012, 45: 8-15.

[5] 程瑶, 梁滔, 赵万华. 动梁式龙门机床双轴同步系统的模型建立及不同步误差分析[J]. 机械工程学报. 2013, 49(13): 174-182.

[6] 程瑶, 赵万华, 李玉霞, 等. 动梁式龙门机床双驱动态不同步误差补偿研究[J]. 中国机械工程,2012, 23(8): 915-919.

[7] 李玉霞, 赵万华, 程瑶. 动梁式龙门机床的双驱同步控制系统建模[J]. 西安交通大学学报,2012, 46(4): 119-124.

[8] MIN X, JIANG S. A thermal model of a ball screw drive system for a machine tool[J]. Jou-rnal of Mechanical Engineering Science, 2011(11): 186-225.

[9] WU C H, KUNG Y T. Thermal analysis for the feed drive system of a CNC machine cent-er[J]. International Journal of Machine Tools and Manufacture, 2003, 43(15): 1521-1528.

(编辑赵蓉)

Measurement and Analysis of Thermal Error in Dual-Drive Feed System

XIA Yang-yu，CHENG Yu，NI Yu-jin，MIAO Hai-jun

(School of Mechanical Engineering, Nanjing University of Science & Technology, Nanjing 210094,China)

Abstract：To investigate the effect of thermal deformation of dual-drive feed system on non-synchronous error, simulation models of dual-screw-driving were established. The feed system steady temperature field was tested. The thermal equilibrium period and the thermal error at different feed rates were analyzed by changing the motor speed, and the variation of non-synchronous error was tested. The non-synchronous error of MCH63 was measured as the tested results to compared with the analysis results by using of Renishaw. The result of simulations and experiments shows that an uneven distribution of temperature field gradient due to synchronous dual-drive structure leads to thermal deformation; The temperature difference and non-synchronous error of the two screw increase with the feed speed when the thermal equilibrium. The growth of finite element simulation and experimental were within 14% and present fluctuant decrease trend, which that proved the correctness of the analysis in theory and simulink.

Key words：dual-drive feed system; thermal deformation; temperature field; non-synchronous error

文章编号：1001-2265(2016)05-0071-04

DOI:10.13462/j.cnki.mmtamt.2016.05.019

收稿日期：2015-06-11

*基金项目：国家科技重大专项(2013ZX04002-011)

作者简介：夏阳雨(1989—)，男，江苏宿迁人，南京理工大学硕士研究生，研究方向为先进加工工艺及装备，(E-mail)xiayangyu880@126.com。

中图分类号：TH161;TG659

文献标识码：A